线阵中基于降维NC—MUSIC的非圆信号DOA估计算法

孙华普+郑旺+吕卫华+张小飞

摘要： 通信领域中非圆（NC）信号的波达方向 （DOA）估计已经得到广泛的研究和应用。 考虑到非圆信号的多重信号分类算法（MUSIC）计算复杂度较高， 提出线阵中基于降维NC-MUSIC的非圆信号DOA估计算法。 与传统的需要二维搜索的2D-NC-MUSIC算法相比， 该算法只需要一维搜索， 降低了计算复杂度。 仿真结果表明， 该算法优于传统的MUSIC算法， 并且与2D-NC-MUSIC算法的估计性能非常接近。

关键词： 线性阵列； 非圆信号； MUSIC； DOA估计

中图分类号： TN911.7文献标识码： A文章编号： 1673-5048（2016）04-0036-06

Abstract： Direction of arrival （DOA） estimation for noncircular （NC） signals has been widely studied and used in communications. Considering the high computational complexity of NC multiple signal classification （MUSIC） algorithm， reduceddimension NCMUSIC algorithm is proposed for DOA estimation of NC signals. Compared with conventional 2DNCMUSIC algorithm which needs twodimension search， the proposed algorithm only requires onedimension search， which reduces the computational complexity. Simulation results illustrate that the proposed algorithm outperforms the conventional MUSIC algorithm and has close estimation performance to the 2DNCMUSIC algorithm.

Key words： linear array； NC signal； MUSIC； DOA estimation

0引言

在阵列信号处理中， DOA估计是一个主要的研究方向， 已广泛应用于通信、 雷达、 声纳和医学图像等领域[1-4]。 传统的DOA估计算法包括MUSIC算法[5] 、 ESPRIT算法[6-8] 、 Capon算法[9-10]及PM算法[11]等， 均已经有了较为成熟的理论， 但估计性能却越来越难以满足要求。 为了提高估计性能， 开始利用信号的非圆特征估计信号的DOA[12-19]。 非圆信号是指在星座图中振幅只有同相分量而正交分量为零的信号， 诸如二进制相移键控（Binary Phase Shift Keying， BPSK）和调幅（Amplitude Modulation， AM）信号等 [20]。 当信源发出非圆信号时， 利用非圆特性， 可以有效地将接收的数据矩阵维数加倍， 从而在提高参数估计性能的同时还能估计出更多的信号源。 因此， 非圆信号的非圆特性已被广泛用于提高DOA估计性能。 文献[12]提出一种非圆MUSIC算法实现DOA估计（NC-MUSIC）。 文献[13]提出非圆信号求根MUSIC算法（Root-NC-MUSIC）， 避免了谱峰搜索。 文献[14]提出一种用ESPRIT实现非圆信号的定位算法， 该算法（NC-ESPRIT）无需谱峰搜索， 复杂度较低。 文献[17]则对非圆信号DOA估计提出一种非圆PM算法， 该算法（NC-PM）比传统的PM算法[12]有着更好的性能。

上述算法的计算复杂度均较高， 尤其是文献[12]提出的2D-NC-MUSIC算法， 需要对DOA和非圆相位进行二维搜索， 计算复杂度较高， 难以应用到实际中。

因此， 为了降低计算复杂度， 在文献[21]面阵降维MUSIC算法的启发下， 结合2D-NC-MUSIC算法二维搜索的特征， 提出了降维NC-MUSIC算法。 仿真结果证明了降维NC-MUSIC算法的有效性。

本文其余部分的结构如下： 第2节介绍了信号的数据模型； 第3节提出了降维NC-MUSIC算法； 第4节对算法进行性能分析； 在第5节中， 仿真结果证明了算法的有效性； 第6节为本文的总结。

1数据模型

一个有M个阵元的线性阵列如图1所示。

降维NC-MUSIC算法的主要步骤如下：

（1） 通过式（4）扩展信号矩阵；

（2） 通过式（28）构造扩展信号的协方差矩阵R^， 并对R^进行特征分解得到噪声子空间U^N， 计算复杂度为O（4M2L+8M3）；

（3） 通过式（29）进行谱峰搜索， 估计信号的DOA， 计算复杂度为O（8M3-4M2K+8（M2+M）n）。

3性能分析

3.1复杂度分析

本文提出的降维NC-MUSIC算法的计算复杂度为O（4M2L+16M3-4M2K+8（M2+M）n）， 而2D-NC-MUSIC算法的计算复杂度为O（4M2L+16M3-4M2K+（4M2+2M）n2）， 其中n为搜索次数。 因此， 降维NC-MUSIC算法比2D-NC-MUSIC算法的计算复杂度低。

在K=3， n=6 000， M=8的情况下， 两种算法的复杂度比较如图2所示。 可以看出， 降维NC-MUSIC算法复杂度较低。

3.2主要优点

本文提出的降维NC-MUSIC算法有如下优点：

（1） 与传统的MUSIC算法相比， 降维NC-MUSIC算法有较好的估计性能， 同时能够估计更多的信号；

（2） 与2D-NC-MUSIC算法相比， 降维NC-MUSIC算法计算复杂度更低；

（3） 与2D-NC-MUSIC算法相比， 降维NC-MUSIC算法拥有相似的估计性能；

（4） 降维NC-MUSIC算法不需要估计非圆相位， 就能很好地估计DOA。

上述讨论中， 假设非圆信号个数K已知。 假设在K未知的情况下， 也能通过信息论中的算法、 矩阵分解算法、 平滑排位算法或者盖氏圆盘算法估计信号个数K[24-27]。

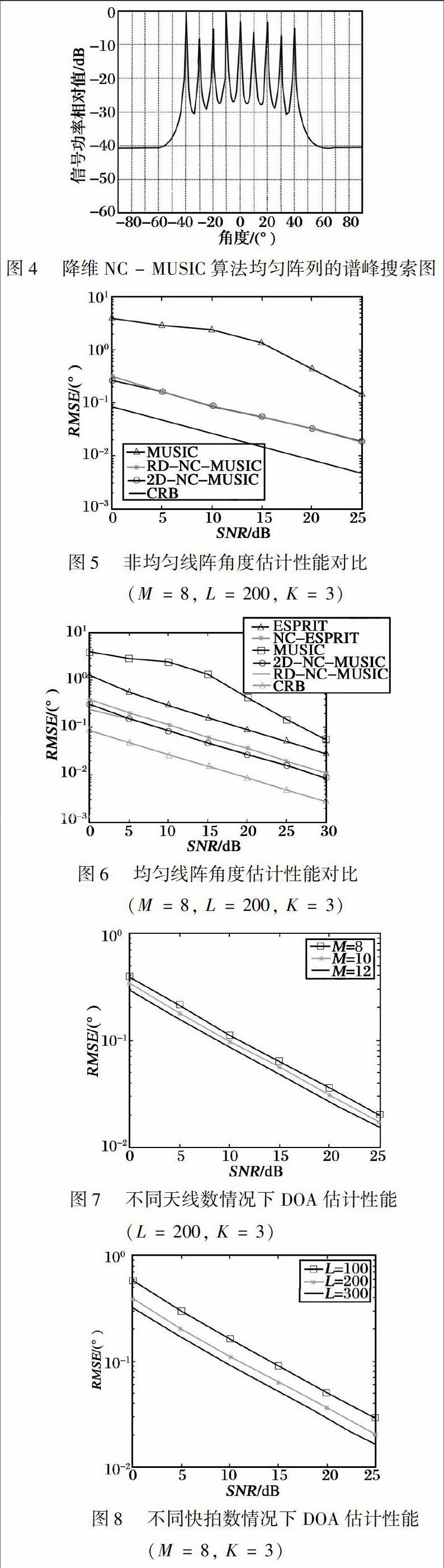
4仿真结果

通过仿真来评估降维NC-MUSIC算法的角度估计性能。

5结论

本文提出了降维NC-MUSIC算法估计非圆信号的DOA。 与传统的MUSIC算法相比， 该算法拥有更好的估计性能， 且能够估计更多的信号。 与2D-NC-MUSIC算法相比， 该算法只需要一维搜索， 在保持估计性能的同时， 有着较低的计算复杂度。 仿真结果证明了算法的有效性。

参考文献：

[1] Krim H， Viberg M. Two Decades of Array Signal Processing Research： The Parametric Approach[J]. IEEE Signal Processing Magazine， 1996， 13（4）： 67-94.

[2] Applebaum S R. Adaptive Arrays[J].IEEE Transactions on Antennas and Propagation， 1976， 24（5）： 585-598.

[3] Li Jianfeng， Zhang Xiaofei. ClosedForm Blind 2DDOD and 2DDOA Estimation for MIMO Radar with Arbitrary Arrays[J]. Wireless Personal Communications， 2013， 69（1）： 175-186.

[4] Bekkerman I， Tabrikian J.Target Detection and Localization Using MIMO Radars and Sonars[J].IEEE Transactions on Signal Processing， 2006， 54（10）： 3873-3883.

[5] Schmidt R O. Multiple Emitter Location and Signal Parameter Estimation[J].IEEE Transactions on Antennas and Propagation， 1986， 34（3）： 276-280.

[6] Zheng Guimei， Chen Baixiao， Yang Minglei. Unitary ESPRIT Algorithm for Bistatic MIMO Radar [J]. Electronics Letters， 2012， 48（3）： 179-181.

[7] Bencheikh M L， Wang Y. Joint DODDOA Estimation Using Combined ESPRITMUSIC Approach in MIMO Radar [J]. Electronics Letters， 2010， 46（15）： 1081-1083.

[8] Zoltowski M D， Haardt M， Mathews C P. ClosedForm 2D Angle Estimation with Rectangular Arrays in Element Space or Beamspace via Unitary ESPRIT [J]. IEEE Transactions on Signal Processing， 1996， 44（1）： 326-328.

[9] 张保锋. 几种DOA估计算法的性能分析[J]. 现代电子技术， 2003（9）： 35-37.

[10] Stoica P， Hndel P， Sderstrm T. Study of Capon Method for Array Signal Processing[J]. Circuits， Systems and Signal Processing， 1995， 14（6）： 749-770.

[11] Marcos S， Marsal A， Benidir M. The Propagator Method for Source Bearing Estimation[J].Signal Processing， 1995， 42（2）： 121-138.

[12] Abeida H， Delmas J P. MUSICLike Estimation of Direction of Arrival for Noncircular Sources[J].IEEE Transactions on Signal Processing， 2006， 54（7）： 2678-2690.

[13] Chargé P， Wang Y D， Saillard J. A Noncircular Sources Direction Finding Method Using Polynomial Rooting[J].Signal Processing， 2001， 81（8）： 1765-1770.

[14] Zoubir A， Chargé P， Wang Yide. Non Circular Sources Localization with ESPRIT[C]∥Proceedings of European Conference on Wireless Technology， Munich， Germany， 2003.

[15] Steinwandt J， Roemer F， Haardt M. Performance Analysis of ESPRITType Algorithms for NonCircular Sources[C]∥International Conference on Acoustics， Speech， and Signal Processing， Vancouver， BC， 2013.

[16] Haardt M， Rmer F. Enhancements of Unitary ESPRIT for NonCircular Sources[C]∥Proceedings of 29th IEEE International Conference on Acoustics， Speech， and Signal Processing， Montreal， Quebec， Canada， 2004.

[17] 孙心宇， 周建江. 非圆传播算子DOA估计算法[J]. 数据采集与处理， 2013， 28（3）： 313-318.

[18] Zhang Xiaofei， Cao Renzheng， Zhou Ming. NoncircularPARAFAC for 2DDOA Estimation of Noncircular Signals in Arbitrarily Spaced Acoustic VectorSensor Array Subjected to Unknown Locations[J]. EURASIP Journal on Advances in Signal Processing， 2013（1）： 1-10.

[19] Liu J， Huang Z T， Zhou Y Y. Azimuth and Elevation Estimation for Noncircular Signals[J]. Electronic Letters， 2007， 43（20）： 1117-1119.

[20] Delmas J P， Abeida H. CramerRao Bounds of DOA Estimates for BPSK and QPSK Modulated Signals[J]. IEEE Transactions on Signal Processing， 2006， 54（1）： 117-126.

[21] Zhang Xiaofei， Xu Lingyun， Xu Lei， et al. Direction of Departure （DOD） and Direction of Arrival （DOA） Estimation in MIMO Radar with ReducedDimension MUSIC[J]. IEEE Communications Letters， 2010， 14（12）： 1161-1163.

[22] 张小飞，汪飞，陈华伟. 阵列信号处理的理论与应用[M].北京： 国防工业出版社， 2013.

[23] Zhong Manli， Fan Zheyi. DirectionofArrival Estimation for Noncircular Signals[C]∥Proceedings of the International Conference on Computer Networks & Communication Engineering， 2013， 30： 634-637.

[24] Wax M， Kailath T. Detection of the Signals by Information Theoretic Criteria[J]. IEEE Transactions on Acoustics， Speech， and Signal Processing， 1985， 33（2）： 387-392.

[25] Di Angzhao. Multiple Sources Location——A Matrix Decomposition Approach[J]. IEEE Transactions on Acoustics， Speech， and Signal Processing， 1985， 35（4）： 1086-1091.

[26] Huang Lei， Long Teng， Mao Erke， et al. MMSEBased MDL Method for Robust Estimation of Number of Sources without Eigendecomposition[J].IEEE Transactions on Signal Processing， 2009， 57（10）： 4135-4142.

[27] Wu H T， Yang J F， Chen F K. Source Number Estimator Using Gerschgorin Disks[C]∥Proceedings of ICASSP， Adelaide， Australia， 1994.

[9] Marcos S， Marsal A， Benidir M. The Propagator Method for Source Bearing Estimation [J].Signal Processing， 1995， 42（2）： 121-138.