先梁后拱法施工轨道交通梁拱体系桥梁吊杆张拉行为研究

刘乐天

(北京城建设计发展集团股份有限公司 北京 100037)



先梁后拱法施工轨道交通梁拱体系桥梁吊杆张拉行为研究

刘乐天

(北京城建设计发展集团股份有限公司 北京 100037)

结合实际工程对梁拱组合体系桥吊杆控制张拉力4种确定方法(倒拆法、正装—倒拆迭代法、无应力状态控制法和影响矩阵法)的实施步骤及结果进行有限元计算研究分析，并针对从拱脚向拱顶、拱顶向拱脚及1/4主跨向两侧3种张拉顺序过程中的结构受力状态进行有限元计算对比分析，结果表明：不同吊杆张拉顺序下各构件均能满足设计需求，但对于体系复杂、规模较大的梁拱组合体系，吊杆张拉过程可能出现部分构件受力超标现象，因此需重视吊杆张拉顺序比选。

城市轨道交通；梁拱组合体系桥梁; 先梁后拱; 杆控制张拉力;吊杆张拉顺序

梁拱组合体系桥梁尤其是下承式梁拱组合体系桥梁，整体刚度大，同时整桥无外部推力，景观优美，具有城市轨道交通对大跨桥梁刚度、景观要求高的特点，因此近年来在轨道交通桥梁中得到越来越多的应用。

梁拱组合体系桥梁通常先要确定一个合理成桥状态，然后再以合理成桥状态为目标按拟定的施工工序确定一个合理施工状态。对于梁拱组合体系桥梁，大都采用先梁后拱的施工方案，其合理施工状态的核心是各吊杆控制张拉力的确定,为此应重点研究两方面问题：一是吊杆控制张拉力的确定方法，二是合理的吊杆张拉顺序。

1 吊杆控制张拉力确定方法概述

吊杆控制张拉力确定方法通常有倒拆法、正装—倒拆迭代法、无应力状态控制法和影响矩阵法等。

1.1 倒拆法

该法以成桥状态为初态，按照施工工序的逆过程，对结构进行倒拆，分析出每拆除一个施工工序对剩余结构的影响，从而推算出各施工阶段的变形和受力状态,该方法一般会遇到结构状态不闭合的问题。

1.2 倒拆—正装迭代法

按既定施工工序的逆序对结构进行倒拆分析，先不计各种非线性问题，然后根据倒拆结果，正装计算，这时计入上轮正装计算时贮存下来的非线性影响值，得到新一轮成桥结果，如此反复几次，即可得到较理想的施工状态。

1.3 无应力状态控制法

无应力状态控制法[1-2]的基本思想是：一定的外荷载、结构体系、支承边界条件、单元的无应力长度、曲率和构形组成的结构，必然唯一地对应一个结构的内力和位移状态，即当结构构件单元的无应力长度和无应力曲率一定时，结构的最终内力和位移状态与结构的施工过程无关。按无应力状态控制法思想，吊杆的无应力长度只有在吊杆张拉时才发生改变，其他荷载作用下吊杆力的变化并不改变吊杆的无应力长度，因此只要使吊杆张拉时的无应力长度与成桥时吊杆无应力长度相同，即可得到合理的吊杆控制张拉力。

1.4 影响矩阵法

该方法按照吊杆的张拉顺序依次求出单位力作用下各吊杆力增量矩阵，然后建立典型方程P0+AT=P(其中，P0为前次张拉后各吊杆的内力矩阵，A为影响矩阵，T为吊杆力增量，P为吊杆张拉目标值)，然后求解线性方程，得出每根吊杆的张拉力增量，各张拉增量与前次各吊杆力相加即为下次吊杆控制张拉力，经过一定次数迭代后即可求得较为精确的吊杆控制张拉力。

2 工程应用分析

宁波轨道交通2号线二期工程跨大运路采用35+

130+35 m下承式单拱肋梁拱组合体系桥梁，桥型布置图见图1。

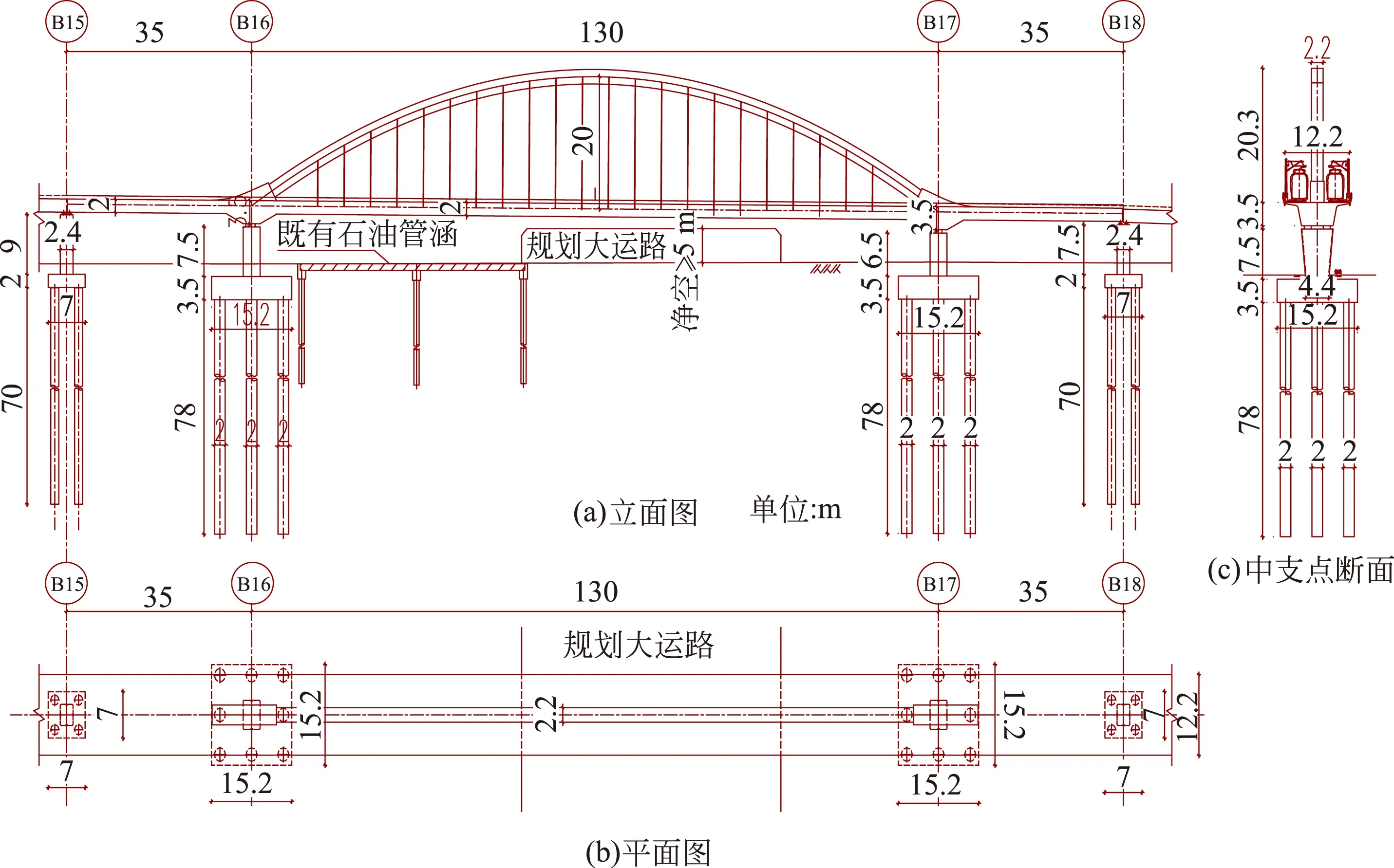
图1 桥型布置图

本桥矢跨比1/6.5，矢高20 m；主梁采用单箱单室断面，标准段梁顶宽12.2 m，标准段梁高2 m，中支点处梁高2.5 m。拱肋采用等高度钢箱结构，拱轴线采用二次抛物线；拱肋截面尺寸为2.2 m×2.2 m。吊索采用55φ7 mm镀锌高强钢丝，间距5 m，横桥向采用双吊杆，锚具采用冷铸锚。

采用先梁后拱的施工方案，主梁采用满堂现浇工法施工，拱肋采用主梁上搭设临时支架拼装的施工方案，吊杆在拱肋拼装完成后逐步张拉到位。

结构计算采用有限元程序MIDAS CIVIL 2010，梁、拱采用空间梁单元，拉索采用桁架单元，为简化计算，横向2根吊杆简化为1根吊杆。

吊杆编号从左至右依次为DG01～DG22，吊杆张拉顺序暂按从拱脚向跨中依次对称张拉，即DG01(DG22)—DG02(DG21)…DG010(DG13)—DG11(DG12)。为方便施工，各吊杆按一次张拉到位原则控制。

2.1 倒拆—正装迭代法

按吊杆张拉顺序逆序倒拆得到的吊杆力为初始张拉力，进行3轮正装迭代计算。各轮吊杆控制张拉力见表1(由于结构对称，仅给出DG01～DG11结果，下同)。

各轮成桥吊杆力与成桥状态吊杆力目标值误差百分比见图2。

表1 各轮吊杆控制张拉力 kN

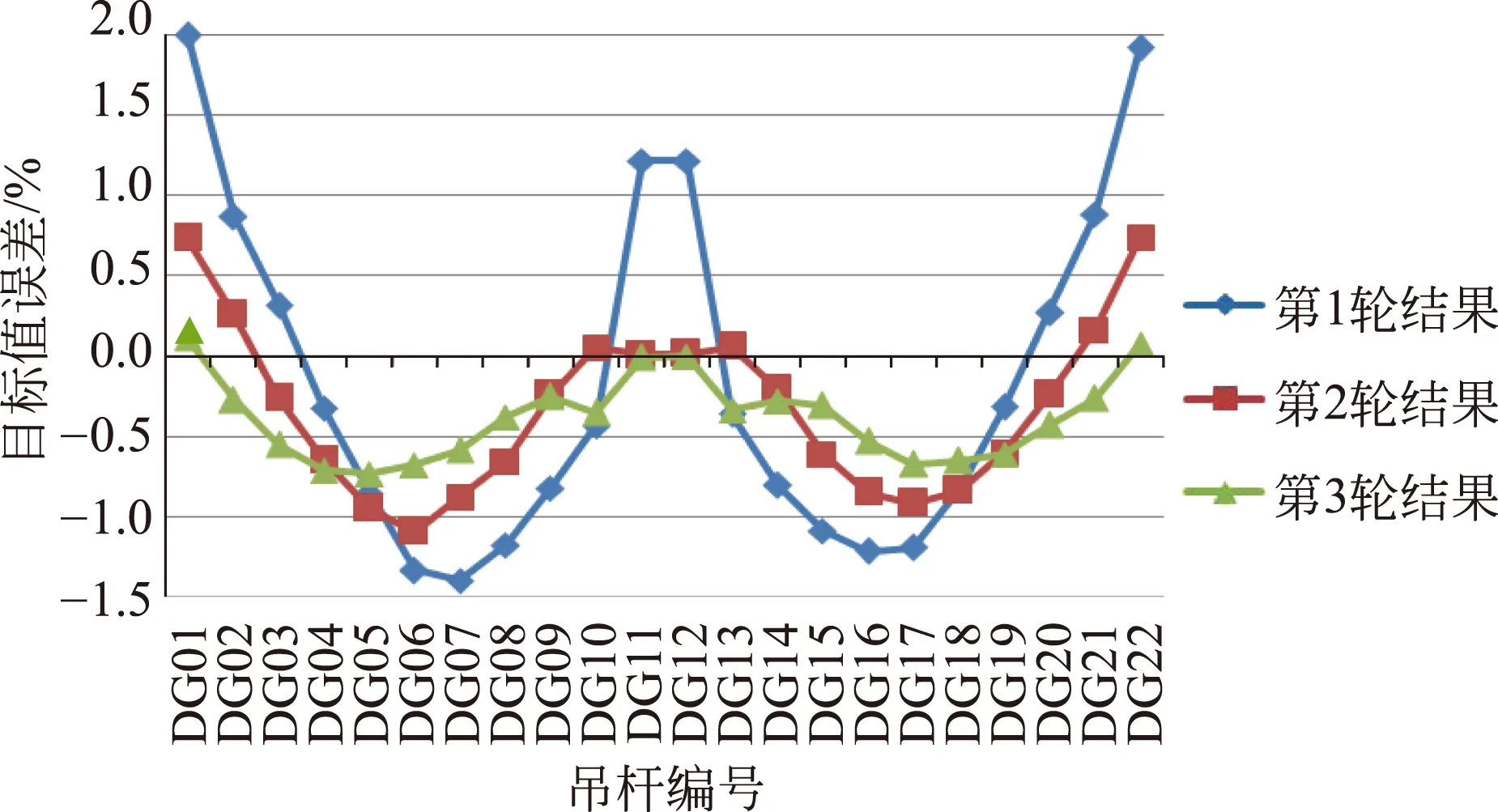
图2 各轮成桥吊杆力与成桥状态吊杆力目标值误差百分比

由图可知，由于本桥采用先梁后拱的施工方案，吊杆张拉前主梁已施工完毕，从吊杆张拉到成桥状态时间较短，徐变等非线性影响较小，因此仅经过3轮迭代过程，成桥索力与目标值误差就已经控制在1.0%之内。

2.2 无应力状态法

无应力状态法第1轮成桥吊杆张拉力采用成桥吊杆力目标值，各轮吊杆控制张拉力见表2，各轮张拉过程中吊杆无应力长度见表3。

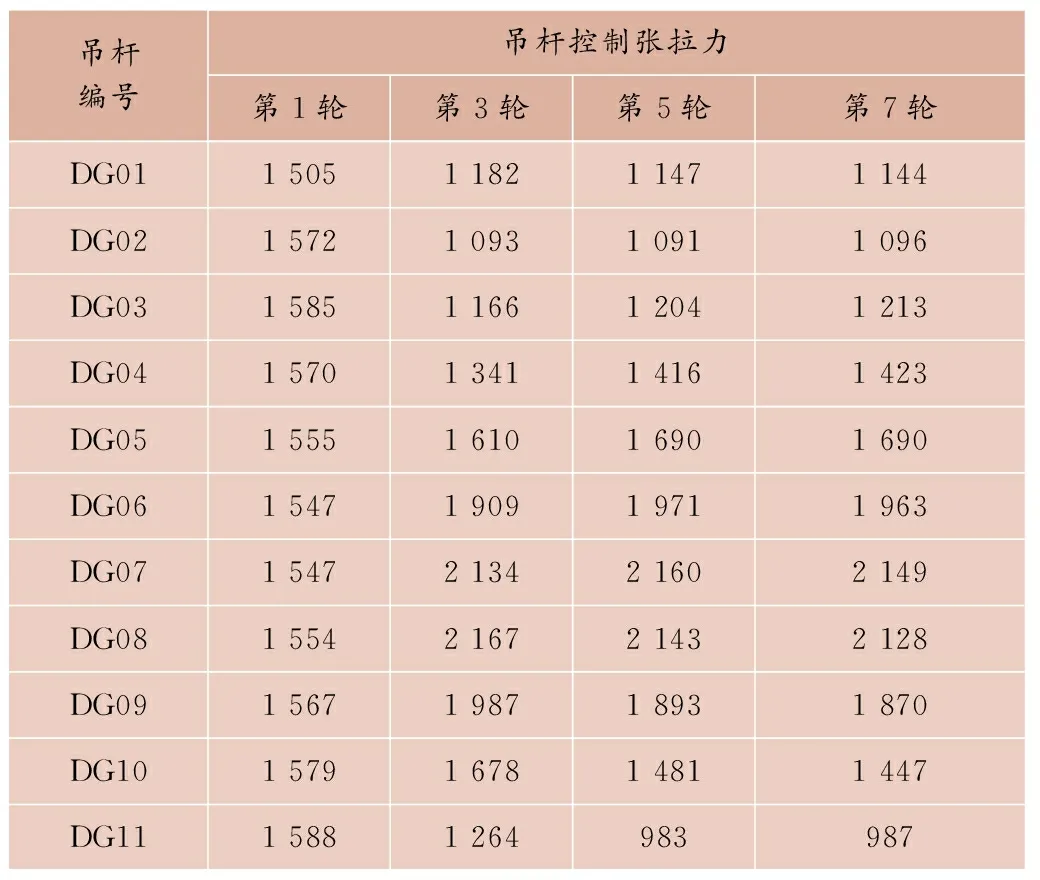
表2 各轮吊杆控制张拉力 kN

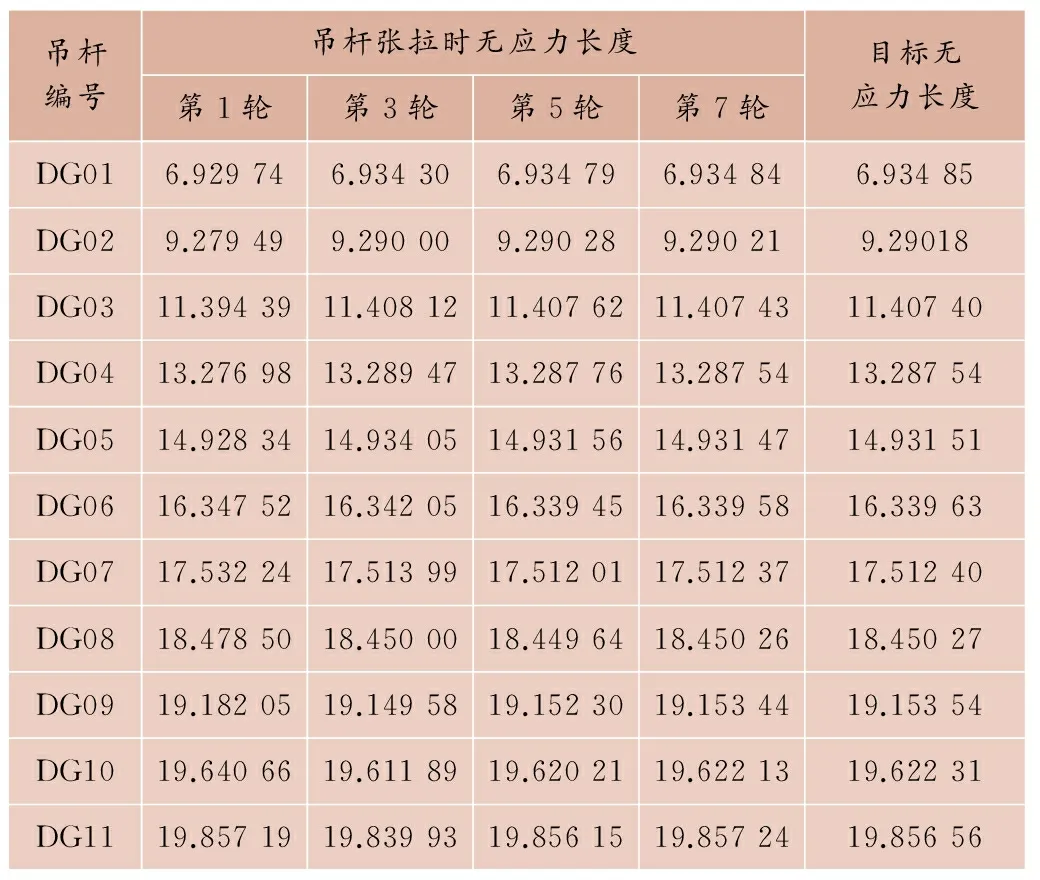
表3 各轮张拉过程吊杆无应力长度 m

各轮张拉过程中成桥吊杆力与成桥状态吊杆力目标值误差百分比见图3。

图3 各轮成桥吊杆力与成桥状态吊杆力目标值误差百分比

由于本桥主梁采用满堂支架现浇，随着吊杆张拉，支架会逐步脱架，也就是在张拉过程中，结构体系在不断发生变化；另外同倒装—正装迭代法不同的是该方法首轮控制张拉力采用成桥吊杆力目标值，与最优吊杆控制张拉力相比偏差较大，因此在张拉过程中支架脱架位置及时间也会和采用最优吊杆控制张拉力张拉时的情况不同，因此出现前几轮DG03、DG07～09、DG10等吊杆张拉过程成桥吊杆力与成桥吊杆力目标值误差相对较大的情况；逼近最优吊杆控制张拉力的速度也较慢，但经过5轮迭代除个别吊杆外，成桥吊杆力与成桥吊杆力目标值误差基本都控制在1%之内。如果按倒拆—正装迭代法的首轮控制张拉力作为无应力状态的首轮控制张拉力，得到的第2轮成桥吊杆力与倒拆—正装迭代法第2轮结果比较见图4。由图可知，第2轮过后无应力状态法成桥索力误差可以达到2%之内，部分吊杆成桥吊杆力与目标值误差还小于倒拆—正装迭代法结果。

图4 倒拆—正装迭代与无应力状态法结果比较

2.3 影响矩阵法

吊杆张拉影响矩阵计算取各吊杆张拉力为1 kN,经过1轮正装计算后求得。第1轮吊杆张拉力以成桥吊杆力目标值作为初始值，各轮张拉过程的吊杆控制张拉力见表4。

表4 各轮吊杆控制张拉力

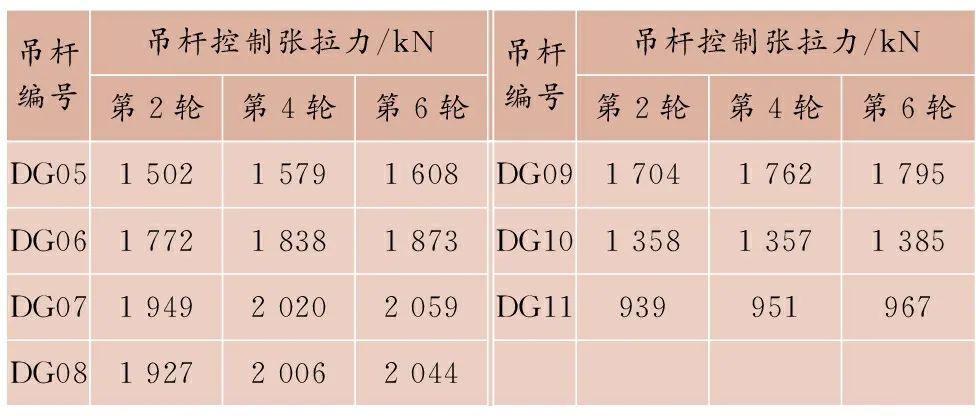
续表

各轮成桥吊杆力值与成桥状态吊杆力目标值误差百分比见图5。

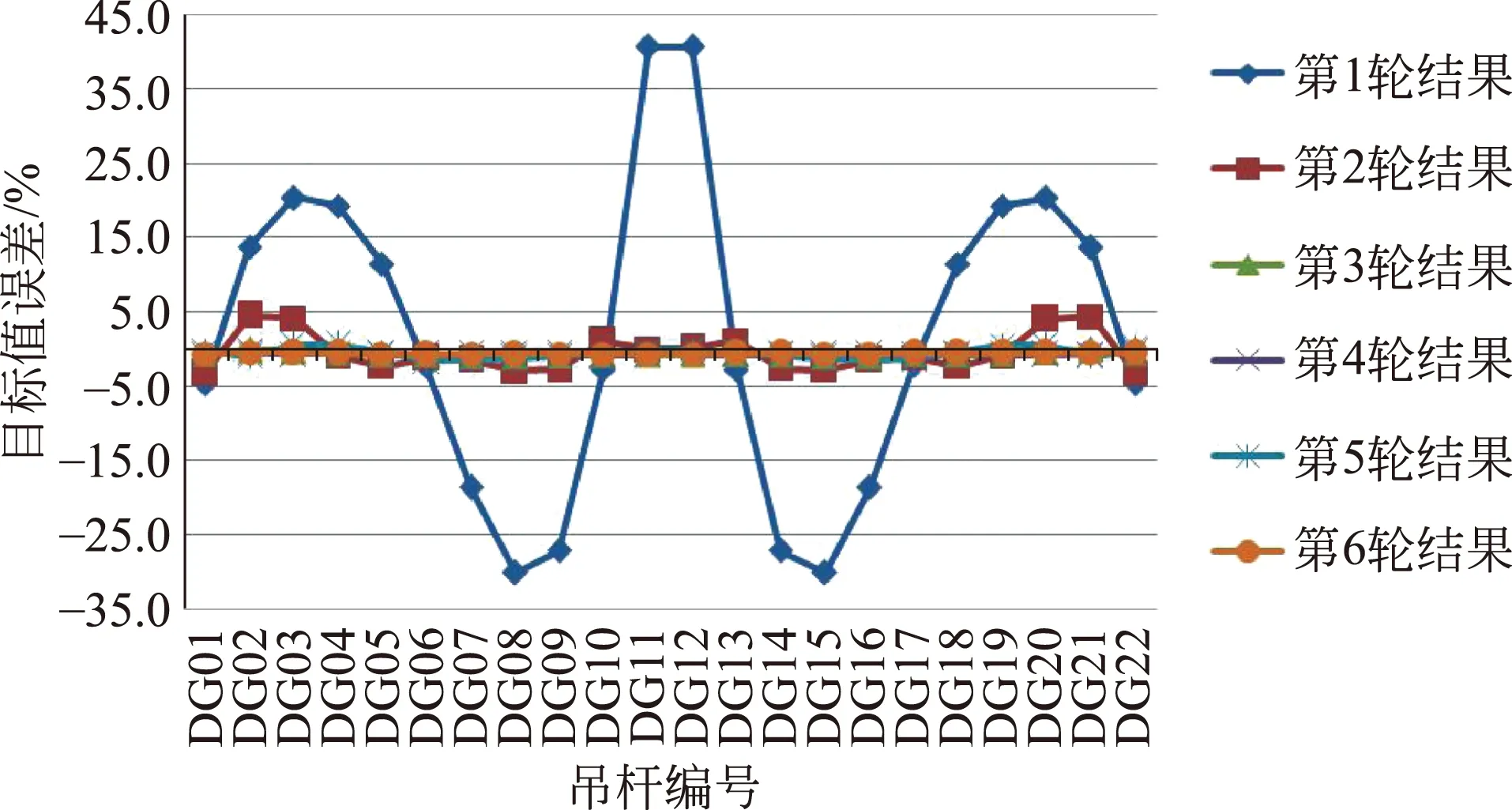
图5 各轮成桥吊杆力与成桥状态吊杆力目标值误差百分比

由上述结果可知，经过4轮迭代后各吊杆成桥吊杆力与成桥状态吊杆力目标值误差都控制在1%之内。由于吊杆张拉相互影响，该方法随迭代次数的增加，各吊杆张拉误差并未递减，而是在一定范围内摆动。另外,同无应力状态法一样，由于首轮控制张拉力选用成桥吊杆力目标值，因此前几轮成桥吊杆力误差相对较大。

3 吊杆张拉顺序研究[3-10]

合理施工状态的研究内容之一是要保证在施工过程中结构要处于一个相对合理的受力状态，而在不同吊杆张拉顺序下，主梁、拱肋、吊杆等受力状态并不一致，因此，有必要研究在不同吊杆张拉顺序下各构件受力情况，一是保证各构件在张拉施工过程中处于安全受力状态，二是还要尽量使张拉过程中结构内力变化幅度较小。下面针对3种不同的吊杆张拉顺序方案进行研究。

方案1：吊杆从拱脚向跨中依次对称张拉，即DG01(DG22)—DG02(DG21)…DG10(DG13)—DG11(DG12)。

方案2：吊杆从跨中向拱脚依次对称张拉，即DG11(DG12)—DG10(DG13)…DG02(DG21)— DG01(DG22)。

方案3：吊杆从1/4跨向两侧依次对称张拉，即DG06(DG17)—DG05(DG18)—DG07(DG16)—DG04(DG19)—DG08(DG15)—DG03(DG20)—DG09(DG14)—DG02(DG21)—DG10(DG13)—DG01(DG22)—DG11(DG12)。

各方案控制张拉力均取各方案正装—倒拆第3轮的结果。各方案吊杆张拉过程中吊杆应力见图6，吊杆应力变化趋势图见图7。

图6 各吊杆应力

图7 吊杆应力变化趋势

从图7可以看出：在吊杆张拉过程中，最大吊杆应力以方案3最大，方案2最小，而且各吊杆应力相对平均。方案1、2吊杆应力变化曲线平滑，方案3吊杆应力变化曲线呈跳跃式变化，变化幅值也较大。

各方案在吊杆张拉过程中拱肋关键截面上缘应力变化趋势图见图8(考虑结构对称仅示出左侧拱肋结果)，应力符号受拉为正，受压为负。

图8 拱肋应力变化趋势

从图8可以看出：方案1三拱肋1/2截面应力变化幅度较大，方案2 1/4截面应力变化幅度较大，3个方案应力幅绝对值相差不大；方案1、2拱肋应力变化曲线平滑，方案3拱肋应力变化曲线呈跳跃式变化。方案1拱肋各截面应力基本都从接近零开始逐步增加，方案2、3都存在部分截面拱肋应力突然增大到一定数值的情况。另外，在张拉过程中拱肋最大压应力方案2最大，方案1最小；最大拉应力方案2最大，方案3最小，由于篇幅受限不再给出图示。

吊杆张拉过程中主梁均处于受压状态，3个方案应力相差不大。各方案在吊杆张拉过程中主梁主跨关键截面上缘应力变化趋势见图9。

图9 主梁应力变化趋势

本工程3个方案在吊杆张拉过程中吊杆、拱肋、主梁应力均满足规范要求，均可采用，但考虑到方案3张拉顺序复杂，吊杆、拱肋应力变化曲线波动相对较大，因此,选择拱肋受力相对较好的方案1。

4 结论

通过上述研究，得出以下几点结论：

1) 对于吊杆控制张拉力的确定方法，倒拆法最为简单，但单纯的倒拆方法无法达到理想的合理施工状态；

2) 正装—倒拆迭代法也相对简单，尤其对于先梁后拱施工方案的梁拱组合体系，从吊杆张拉到成桥状态过程中徐变等非线性影响较小，另外首轮吊杆控制张拉力采用倒拆结果，因此通过次数不多的迭代后，基本可求出合理的吊杆张拉力；

3) 采用无应力状态控制法，当首轮吊杆控制张拉力选用成桥吊杆力目标值时，在张拉过程中支架脱架位置、时间与采用最优吊杆控制张拉力张拉时情况不同，因此逼近最优吊杆控制张拉力的迭代次数会增多，而且前几轮误差会相对较大；

4) 影响矩阵法同无应力状态法一样，迭代的次数及前几轮误差也受首轮吊杆控制张拉力选用的影响；同时由于吊杆张拉相互影响，随迭代次数的增加，各吊杆张拉误差不一定递减，而是在一定范围内摆动；

5) 由于非线性等原因的存在，上述方法都需通过迭代计算来达到较为满意的结果；

6) 在不同吊杆张拉顺序下吊杆、拱肋、主梁等各构件受力会出现一定程度的差别，由于本桥规模不算太大，不同吊杆张拉顺序下各构件均能满足设计需求，但对于体系较为复杂、规模较大的梁拱组合体系，在吊杆张拉过程中可能会出现部分构件受力超标现象，因此应重视吊杆张拉顺序的比选。

[1] 刘乐天.轨道交通特殊桥梁选项研究[J].都市快轨交通,2013,26(4):28-33.

[2] 刘乐天.高低塔斜拉桥静力性能研究及施工控制[D].长沙：长沙交通学院,2002:43-45.

[5] 秦顺全.斜拉桥安装无应力状态控制法[J].桥梁建设，2003(2):31-34.

[6] 朱小秀,孙久春.系杆拱桥吊杆各种张拉索力计算方法和比较[J].中国市政工程，2010(3):21-23.

[7] 李晓林,杨树萍.两种吊杆张拉方法的研究[J].工程与建设，2012,26(1):107-111.

[8] 隋云龙,刘波.系杆拱桥吊杆施工张拉力迭代算法研究[J].北方交通，2014(9):10-12.

[9] 梁海灵.大跨度单肋拱桥吊杆张拉过程分析[J].交通科技,2013(3)：5-8.

[10] 李新平,钟健聪.空间系杆拱桥吊杆张拉控制分析[J].华南理工大学学报(自然科学版), 2004,32(7):89-92.

(编辑：郝京红)

Suspender Tension Method of Beam-arch Combined Bridge with Beam-first-and-arch-next Construction Craft for Rail Transit

Liu Letian

(Beijing Urban Engineering Design and Research Institute Co., Ltd., Beijing 100037)

Four kinds of suspender tension methods (dismantling suspender tension in reverse order, remove-installation iteration method, no stress state control method and impact matrix method) of beam-arch combined bridge are studied, and implementation steps and the results of different methods are given. In addition, the stress states of structure in different tensioning sequence (from the arch foot to vaults, from vaults to the arch foot and from the quarter of the main span to both sides) are studied. The research provided the basis for the suspender tension behavior. The results show that the components can meet the design requirements in the sequence of different hanger rods, while for the complex and large-scale beam-arch combined bridge system, the tension of some members will exceed the specification in the tension process of the hanger rod. Therefore, it is necessary to pay attention to the suspender tension sequence.

urban rail transit; beam arch combined bridge; beam-first-and-arch-next; suspender tension; suspender tension sequence

10.3969/j.issn.1672-6073.2016.05.018

2016-03-23

2016-04-18

刘乐天，男，硕士研究生，高级工程师，从事轨道交通及市政桥梁设计，liuletian2002@126.com

U231

A

1672-6073(2016)05-0088-06