一类带扰动的风险模型的预警区问题
2016-11-28魏瑞雪余国胜熊昕
魏瑞雪,余国胜,熊昕
(江汉大学数学与计算机科学学院,湖北 武汉 430056)
一类带扰动的风险模型的预警区问题
魏瑞雪,余国胜,熊昕
(江汉大学数学与计算机科学学院,湖北 武汉 430056)
讨论带扰动的风险模型的预警区问题,此模型保费收入过程是复合Poisson-Geometric过程,两类理赔计数过程分别为独立的复合Poisson-Geometric过程和广义Erlang(n)计数过程,得到此模型的第一预警区的一个条件矩母函数所满足的积分-微分方程.
风险模型;第一预警区;条件矩母函数;积分-微分方程;Laplace变换
0 引言
研究保险精算风险理论中的预警区问题可以为保险公司决策者提供一个早期风险警示.于金酉等[1]讨论了常利率复合Poisson风险模型中的预警区问题.崔巍等[2]研究了一类推广的复合Poisson-Geometric风险模型的预警区问题.文献[3]中充分应用盈余过程的强马氏性,讨论了一类复合Poisson-Geometric风险模型的第一个预警区的一个条件矩母函数.文献[4]中对于一类常利率复合Poisson-Geometric风险模型的第一预警区问题进行了研究,得到第一预警区的一个条件矩母函数所满足的积分——微分方程,在指数理赔的特殊情况下给出精确解.赵明清等[5]在复合Poisson-Geometric风险模型的基础上,引入利率因素,研究了常利率复合Poisson-Geometric风险模型的预警区问题.文献[6]中得到了多险种多复合Poisson-Geometric常利率风险模型第一预警区的一个条件矩母函数所满足的积分-微分方程.近年来,带扰动的风险模型正越来越受到人们的关注.Chiu等[7]考虑了带扰动的经典风险模型.文献[8]中考虑带扰动的两类理赔风险模型的罚金折扣函数,两类理赔来到的计数过程分别为独立的Poisson过程和广义Erlang(n)过程.文刘震[9]等在文献[8]的基础上进行推广,研究了带扰动相关理赔下的风险模型的罚金折现函数.本文中在带扰动的风险模型下讨论预警区问题.这里我们对模型作进一步假设如下:
(1)

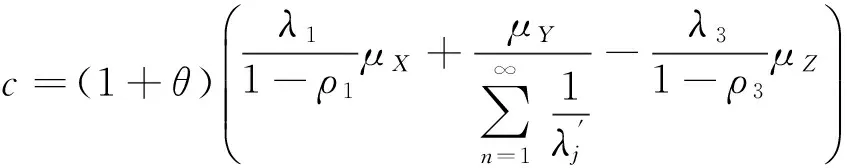


1 预备知识及引理
为此先介绍Poisson-Geometric过程的定义如下:
定义1.1[10]设λ>0,0≤ρ<1,称{N(t);t≥0}为参数λ,ρ复合Poisson-Geometric过程,如果满足:
i)N(0)=0;
ii) {N(t);t≥0}具有平稳独立增量;
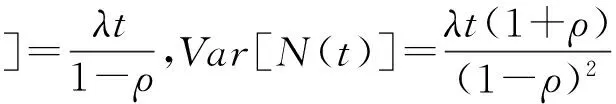
注1.1 由定义1.1,当ρ=0时,复合Poisson-Geometric过程就是Poisson过程.因此,复合Poisson-Geometric过程是Poisson过程的一种推广.
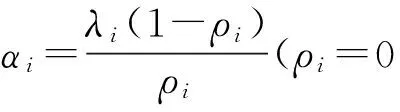
P{Ni(t)=0}=e-λit=1-λit+o(t),
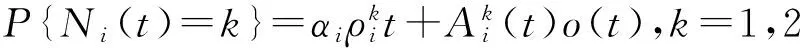
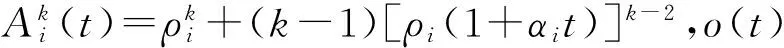
2 Φ(-z,0,r)所满足的积分-微分方程
定理2.1 记
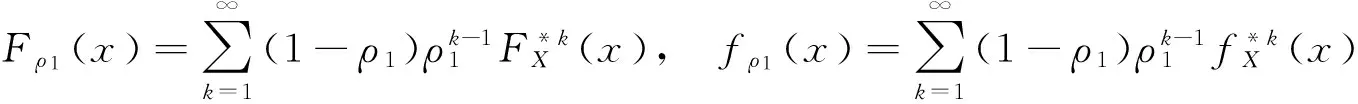
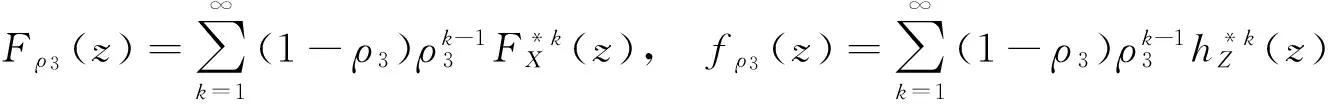
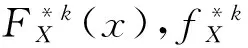
(2)
(3)
定理2.1的证明 在充分小的时间(T,T+dt]内考察风险模型,记
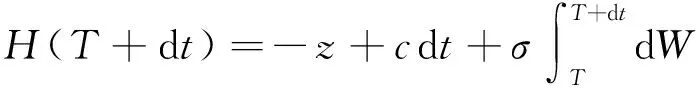
对j=1,2,…,n-1,则由全期望公式及引理1.1有
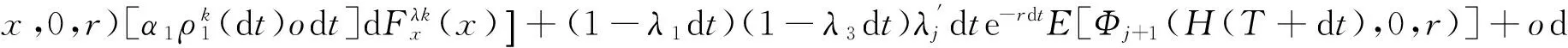
由泰勒展开式及Ito公式得
(1-λ1dt)(1-λ3dt)λjdte-rdtE[Φj+1(H(T+dt),0,r)]+o(dt).
对上式整理并令dt→0,化简得
(4)
对起始状态为n,有
(5)
对上式整理化简得
(6)
对上式整理并令dt→0,化简得
(7)
注2.1σ=0,n=0,ρ1=0,ρ3=0,λ3=0,则(2)式为文献[1]中的(2.1)式.
注2.2δ=0,σ=0,c=0,n=0,ρ3=0,则(2)式为文献[2]中的(3.1)式.
注2.3δ=0,σ=0,n=0,ρ3=0,λ3=0,则(2)式为文献[3]中的(3)式.
注2.4σ=0,c=0,n=0,ρ3=0,λ3=0,则(2)式为文献[4]中的定理1.
注2.5σ=0,c=0,ρ3=0,n=0,则(2)式为文献[5]中的(2)式.
3 Φj(-z,0,r)的Laplace变换
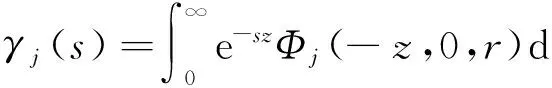

fρ1(x)是参数为α1=(1-ρ1)β1的指数分布的概率密度.同样道理可得fρ3(z)是参数为α3=(1-ρ3)β3的指数分布的概率密度.假设{Yi;i≥1}服从参数为α2的指数分布.则定理2.1为
(8)
(9)
将(8)式两边关于z求导,并将(8)式两边同乘-α1与之相加整理可得
(10)
将(9)式两边关于z求导,并将(9)式两边同乘-α1与之相加整理可得
(11)
对(11)式两边关于z求导,并将(11)式两边同乘-α2与之相加整理可得
λ3(α1+α3)(α2+α3)e-α3z=0
(12)
(13)
(14)
令
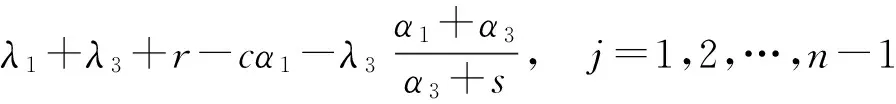
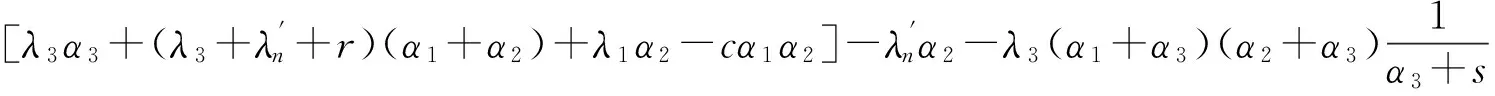
其余aij(s)=0.再令A(s)=(aij(s))n×n,γ(s)=(γ1(s),γ2(s),…,γn(s))T,b(s)=(b1(s),b2(s),…,bn(s))T,T表示转置.由(13)~(14)式可得
A(s)γ(s)=b(s)
(15)
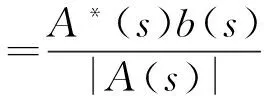
下面举一个例子:若假设{Xi;i≥1},{Yi;i≥1},{Zi;i≥1}均服从参数为1的指数分布.例如:取
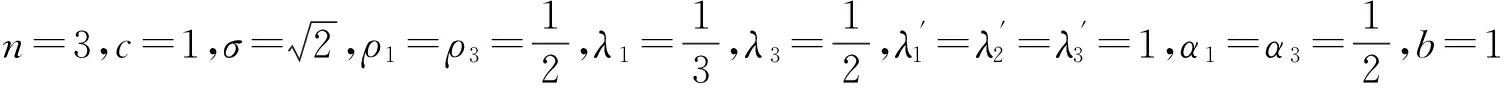
此时
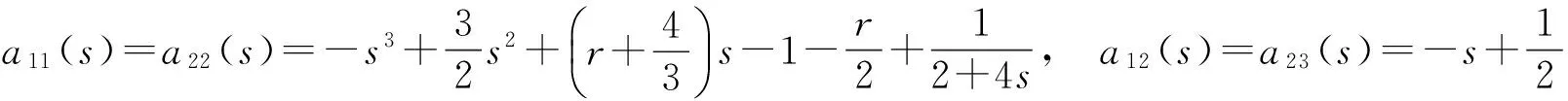
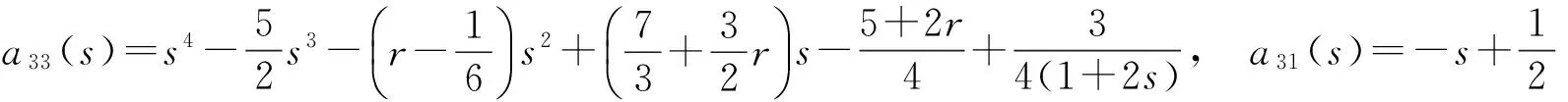
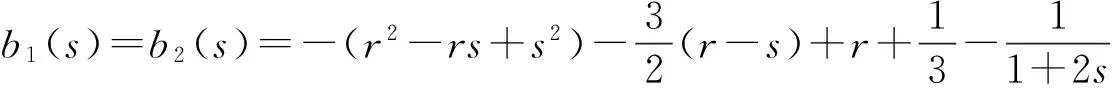
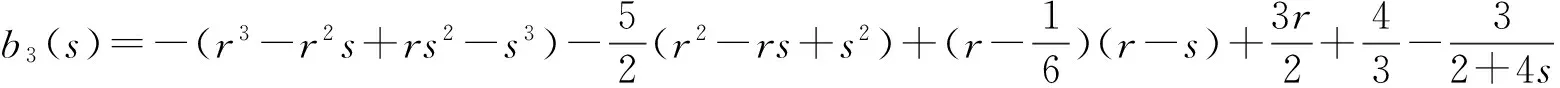
由(15)式可得

其中

[1] 于金酉,胡亦钧,韦晓.常利率复合Poisson风险模型中的预警区问题[J].数学物理学报,2010,30A(1): 1-17.
[2] 崔巍,余旌胡.一类推广的复合Poisson-Geometric风险模型下预警区问题的研究[J].数学物理学报,2012,32A(1): 27-40.
[3] 钟朝艳. 复合Poisson-Geometric风险模型的预警区问题[J].经济数学,2012,29(2):83-86.
[4] 钟朝艳.一类常利率复合Poisson-Geometric风险模型的预警区问题[J].西南师范大学学报(自然科学版),2014,39(3): 36-40.
[5] 赵明清,尚鹏,李田.一类推广的常利率复合Poisson-Geometric风险模型的预警区问题[J].经济数学,2015,32(1):1-5.
[6] 贺小丽,余国胜.多险种多复合Poisson-Geometric常利率风险模型预警区问题[J].湖北大学学报(自然科学版),2016,38(1):18-24.
[7] Chiu S N,Yin C C.The time of ruin,the surplus prior to ruin and the deficit at ruin for the classical risk process perturbed by diffusion[J]. Insurance: Mathematics and Economics,2003,33:59-66.
[8] 赵永霞,王春伟. 带扰动的两类索赔风险模型的罚金折扣函数[J].高校应用数学学报A辑:2010,25(3):263-272.
[9] 刘文震,王传玉. 带扰动的两类相关索赔风险模型的折现罚金函数[J].中国科学技术大学学报,2013,43(6):444-454.
[10] 毛泽春,刘锦萼.索赔次数为复合Poisson-Geometric过程的风险模型及破产概率[J].应用数学学报,2005,28(3):419-428.
(责任编辑 赵燕)
The analysis of the duration of negative surplus for a perturbed risk model
WEI Ruixue,YU Guosheng,XIONG Xin
(School of Mathematics and Computer Science,Jianghan University,Wuhan 430056,China)
We discussed the duration of negative surplus for a perturbed risk model.It was assumed that the income of insurance premiums was a compound Poisson-Geometric process and the corresponding claim computation processes were either independent compound Poisson-Geometric process or generalized Erlang(n) process.The integral-differential equations of a conditional moment generating function for the first duration of negative surplus had been obtained.Then the explicit expression about the Laplace transforms of the conditional moment generating function for the first duration of negative surplus is obtained when the premium and the claims are exponential distributions.Finally we gived an example to illustrate our results.
risk model; first duration of negative surplus;conditional moment generating function; integral-differential equation; Laplace transform
2016-04-27
武汉市教育局2015年市属高校教学研究项目(2015057)资助
魏瑞雪(1996-),女,本科生;余国胜,通信作者,讲师,E-mail:guosyujianghanun@126.com
1000-2375(2016)06-0488-07
O211
A
10.3969/j.issn.1000-2375.2016.06.004
当保单的价格,两类理赔额分布密度均服从指数分布的条件时,给出此模型的第一预警区的一个条件矩母函数的Laplace变换的表达式,并给出实例以说明所得结果.
