基于Lorenz超混沌理论的数字图像加密算法研究

张错玲,韦良芬

(安徽三联学院计算机工程学院,安徽 合肥,230601)



基于Lorenz超混沌理论的数字图像加密算法研究

张错玲,韦良芬

(安徽三联学院计算机工程学院,安徽 合肥,230601)

在经典的Lorenz混沌系统基础上经过一定的变换得到Lorenz 4D超混沌系统，接着描述Lorenz 4D超混沌系统的加密算法，并给出了仿真实验结果及对结果的安全性分析.

混沌；Lorenz系统；图像加密；4D超混沌系统

0 引言

随着计算机技术、信息技术和网络通信技术的迅速发展，利用网络来传输数字化的信息已经变得越来越普遍，这些信息不仅包括文本类信息，还包括声音、视频、图像等多媒体信息.然而，图像的信息量大、冗余度高等特点又给其加密带来了一定的困难，因此，传统的加密方式已不适合数字图像加密；而混沌系统的伪随机性、长期的不可预测性及对初值的极端敏感性等特点，使其非常适合于数字图像的加密[1].

目前关于Lorenz混沌系统的数字图像加密算法的研究基本上都是三维的，基于超混沌系统的图像加密算法的研究还相对较少，而本文中研究的内容就是基于4D超混沌系统的数字图像加密算法，该加密系统是在Lorenz系统中第二个线性方程中又加入一个控制器.这样的超混沌系统实际上是利用线性控制Lorenz[2]系统.在此加密算法中，一个来自外部的128 bit的密钥作为映射系统的参数，这些参数是产生混乱的二进制序列矩阵.此外，前一个子图像块的加密结果将被应用到下一个子图像块加密过程中.通过计算机的仿真结果表明，下面描述的算法具有一定的优越性和可取性，其可以实现一个较好的安全加密效果.

1 Lorenz超混沌系统

经典的Lorenz系统是洛兹在1963年提出的第一个混沌模型，Lorenz系统的线性方程描述如下[3]：

(1)

其中a,b,c是控制参数，且当a=10，b=8/3，c=28时，系统处于混沌状态.但为了获得超混沌状态，还要考虑一下两个重要条件[6]：

i) 嵌入一个超混沌吸引子相空间的最小尺寸应该至少有4个，这就明表最低需要4个一阶耦合自治的常微分方程.

ii) 引起不稳定耦合方程的数目应该至少有两个，其中至少有一个是非线性的.

通过引入公式(1)中第二个方程的非线性反馈控制系统，得到了以下的四维超混沌系统：

(2)

上式中k是一个待定常数.为了简化，在下面的内容中将式(2)称为4D超混沌Lorenz系统.试验的数值表明，当a=10，b=8/3，c=28时，4D系统具有两个正Lyapunov指数的混沌吸引子：λLE1=0.399 7，λLE2=0.311 3(另外两个是λLE3=0，λLE4=-14.3776).另外，实验结果还表明，当k∈[0,16.6]时，该系统是超混沌状态且有两个Lyapunov指数；而当k∈(16.6，21.75]时，该系统只是混沌系统且只有一个正的Lyapunov指数[4].由此可知，通过一些简单的控制输入，4D系统具有很强的产生复杂混沌与超混沌吸引子的能力,使系统具有更好的安全性.

图1 经典Lorenz系统的混沌吸引

2 基于超混沌系统的图像加密算法描述

在本节中提出的加密算法是基于Lorenz超混沌系统的，为了使算法的描述更容易理解，下面列出其中的一些数学符号及其含义：

K1,K2,…,K16：是128bit的密钥；iw,ih：分别表示图像的宽和高；

S>>α：表示S循环右移α位；K1⨁K2：表示K1和K2的异或运算.

具体算法描述如下：

Step1. 输入一个128 bit的原始图像和密钥,通过以下计算过程得到算法中的4个参数：

Step2. 通过以下方法确定(公式2)中的初始条件(x0,y0,z0,u0)，控制参数k及迭代次数N的值：

依据龙格-库塔方法[5]，让系统(式2)中从初始条件(x0,y0,z0,u0)开始遍历N次.为了避免瞬态效应，这里迭代从200次以后开始.

Step3. 让(xN,yN,zN,uN)表示系统(式2)中的N次迭代，使xN=0.b1(x)b2(x)…bi(x)…,且bi(x)表示如下：

Step4. 加密第i个原子图像块mib的公式如下：

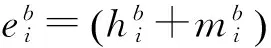
Step5.

如果所有的原子图像块都被加密，则算法结束，输出加密图像；否则，继续执行Step3到Step5.

对于以上的加密过程有以下几点说明：

① 控制参数k的取值范围为k∈[0,16.6],以确保在超混沌状态下有两个正的Lyapunov指数.

③ 很显然，生成的密钥流eib是依赖于密码体制和明文的，且在Step5的反馈机制中，流密码是更复杂和难以预测的.这就加强了密码系统的安全性.

3 算法仿真实验及安全性分析

对于图像加密来说，一个有效的加密算法应该具有抵御多种已知攻击的能力.下面针对提出的算法进行敏感性、密钥空间、直方图、信息熵和差分攻击几个方面做安全性分析[6]并给出相应仿真实验结果.

3.1 敏感性分析 对敏感度分析，主要是从密钥和被加密的明文两个方面来进行试验的.

假设原始图像“tree.jpg”的尺寸大小为256×256，取密钥K1=“Kab4547MN78xy”,K2=“Jab4547MN78xy”，图2则是基于此算法的实验结果.从结果可以看出：分别使用密钥K1和K2时，得到的加密图像(b)和(c)明显不同.将原图(a)中坐标为(50,50)的像素灰度值微小改变，而密钥依然为K1时，得到的加密图像为图(d)，显然图(b)和图(d)也是完全不同的.由此可以看出，该算法对密钥的敏感度比较高.3.2 密钥空间分析 密钥空间安全性分析使用的是穷举法，也就是对所有可能的密码进行逐一推测、验证和排除，直到找到正确的密码为止.因此，为了抵御穷举法对密码的破译，加密的密钥空间必须要足够大.本文中所提出的基于4D Lorenz超混沌算法中加密密钥Ki依赖的参数有{a,b,c,x0,y0,z0,u0,k,N}，而现代计算机的计算精度一般都可以达到15位有效数字，即使进行一次迭代，则密钥空间也可以达到1075.因此，此算法密钥空间足够大，使用穷举破译根本不可能实现.

3.3 直方图分析 图3为原始图像和加密后图像及各自对应的灰度直方图.由此可以看出加密后图像的直方图呈均匀分布，掩盖了原有图像的分布规律，说明此算法的加密效果是非常成功的.

图3 图像加密前后灰度直方

3.4 信息熵分析 众所周知，明文m的信息熵H(m)可以通过以下的公式得出：

(3)

其中p(mi)表示信息mi在图像中出现的概率，n的值取256.对于一个具有256级的灰度图像，如果每一个灰度值的概率是相等的，则信息熵为8，说明该图像是随机性较好.如果信息熵小于8时，说明该图像存在一定程度上的可预见性，则威胁图像的加密效果.因此，加密图像的信息熵越接近理想值，则越能抵御熵收到的攻击.

表1 原始图像与对应加密图像的信息熵

表1显示了4个不同原始图像和对应加密图像的信息熵计算结果，从结果不难发现：所有原始图像的信息熵都小于理想值，这说明实用信息源很难具有随机性；但每个加密后图像的熵非常接近于理想值，表示前面描述的加密算法是足够安全的，可以抗击熵的攻击.

3.5 差分攻击 为了检测原始图像中任一像素的变化对加密后整个图像的影响，通常采用两种测试方法，即NPCR(像素数量变化率)和UACI(统一平均变化强度)[7].NPCR测试的是两副图像之间像素数的不同，而UACI测量的是两副图像之间平均强度的差异，其分别定义如下：

(4)

(5)

其中，E1(i,j)和E2(i,j)分别表示两个加密图像在点(i,j)处的灰度值，W和H分别表示图像的宽度和高度.取一个与E1(i,j)和E2(i,j)同样大小的阵列D(i,j)，如果E1(i,j)=E2(i,j)，则D(i,j)=1；否则D(i,j)=0.

随机对原始图像上的一个像素值作微小变动，对修改后的图像加密，计算NPCR和UACI的值.取多次试验的平均值得到NPCR=99.2%、UACI=34.3%.实验结果表明，原始图像的任何一点改变都将会导致加密图像的巨大变化，所以说该加密方案具有非常优良的抵抗差分攻击的能力.

4 展望

目前，混沌技术应用于数字图像加密领域还有很多问题亟待解决，要实现其广泛的应用还有很长的路要走.笔者拟在以下几个方面继续进行研究：

1)当前，利用混沌来构造公开密钥密码的研究成果还较少，笔者认为对此方向的研究应该具有一定的现实意义.

2)如何实现混沌加密技术和数字图像压缩技术的完美融合.由于数据量大、冗余度高的特点使得直接添加压缩功能的图像加密非常诱人.如能实现两者的有机结合，则数字图像加密一定会有一个美好的前景.

[1] 秦明甫.基于混沌理论的数字图像加密研究[D].重庆：重庆大学计算机学院，2009.

[2] 王光义，郑艳，刘敬彪. 一个超混沌Lorenz吸引子及其电路实现[J].物理学报，2007(6):3113-3120.

[3] 刘式达，梁福明，刘式适，等.自然科学中的混沌与分形[M].北京：北京大学出版社,2003.

[4] 梁美灵，王则柯.混沌与均衡纵横谈[M].大连：大连理工大学出版社，2008.

[5] 禹思敏，林清华，丘水生.四维系统中多涡卷混沌与超混沌吸引子的仿真研究[J].物理学报，2003，52(1)：25-33.

[6] Wong Wai-Kit ,Lee Lap-Piu, Wong Kwork-Wo.A modified chaotic cryptographic method[J].Computer Physics Communications，2001，138(3):234-236.

[7] Chen G,Mao Y,Chui C.Symmetric image encryption scheme based in 3D chaotic cat ps[J]. Chaos，Solitons & Fractals，2004,21(3):749-761

[8] 廖建华.基于混沌理论的数字图像加密技术研究[D].湖南：中南大学，2010.

[9] Somaya Al-Maadeed,Afnan Al-Ali,Turki Abdalla,et al.A new chaos-based image-encryption and compression algorithm[J]. Journal of Electrical and Computer Engineering，2012.

[10] 谭琳.基于DNA序列和混沌的图像加密算法[J].信息系统工程,2014(11):90-92.

[11] 蔡俊，陈昕，向旭东.一种基于混沌的代换-置换结构图像加密算法[J].计算机科学,2014(09):158-164.

(责任编辑 江津)

Research on digital image encryption algorithm base on Lorenz hyper chaos

ZHANG Cuoling,WEI Liangfen

(Department of Computer Science,College of Anhui Sanlian,Hefei 230601,China)

On the basis of classic Lorenz chaos system, we obtained the Lorenz 4D hyper chaos system by the certain transform，then described the Lorenz hyperchaos system of 4D encryption algorithm，and gave the simulation experiment results and security analysis.

chaos; Lorenz system;image encryption; 4D hyper chotic system

2016-02-18

安徽省教育厅自然科学重点项目(KJ2016A252)资助

张错玲(1982-)，女，硕士，讲师；韦良芬，通信作者，副教授

1000-2375(2016)06-0551-06

O211.4

A

10.3969/j.issn.1000-2375.2016.06.014