理清来龙去脉 分析临界状态

宋浩杰

高中物理涉及到临界的问题学生往往比较头疼。什么是临界问题呢？当物体由某种状态转变成另一状态的过程中，中间某个质变的转折点则可对应为临界状态，物理学上有关临界状态的问题研究就称为临界问题。教师引导学生处理相关问题时，切忌让学生对临界条件死记硬背，而要帮助学生通过对量变过程的分析，来认识质变的必然。笔者以高一阶段的几个典型临界问题为例，谈谈自己对此类内容进行教学时的思考。

1有关速度的临界问题

运动学的临界问题经常出现在追及情形中。追及问题就是讨论两个物体在运动过程发生追赶或相遇的问题。此类问题中的物体都有不同的运动状态，这就导致彼此间距离的变化需要进行定量的计算分析，再因为初态二者间的距离或大或小，则会发生没有追上或追上的可能。这时就会有一个临界状态的讨论，此类问题的难点在于，学生不仅要对两个物体的不同运动状态进行分析，还要对物体的空间关系、速度关系进行研究。

例1 现有货车甲从某地沿直线以20 m/s的速度向前匀速行驶，轿车乙在甲出发了200 m之后，从同一位置由静止状态开始，以加速度2 m/s²向前匀加速去追赶甲车。求轿车在追上货车之前二者之间的最大的距离。

分析

本题处理的关键在于学生必须理顺两辆汽车之间的空间位置的变化关系，一项重要的辅助手段是画出汽车行进的示意图（如图1所示）。s₀是乙车出发时，甲车已经领先的距离，此时乙车速度为零，它还有一段逐渐加速的过程，在乙车速度小于甲车的阶段，二者的距离会逐渐变大；随着乙车的速度不断增加，当乙车速度超过甲车后，二者距离逐渐减小；因此甲乙二车速度相等的时刻就是彼此距离增大和缩短的分界点，也就是我们所说的临界状态。所以，解题步骤为两个部分，第一求出乙车速度增加至20 m/s所对应的时间，第二在这段时间里甲车和乙车分别发生的位移，二者相减之后再加上原有的200 m的距离，即为答案。

进一步的思考：本题的处理还有相对运动法、图象法以及二次函数求极值的方法，笔者认为前两种方法属于物理思维的积极体现，第三种方法需要学生建立数学模型来进行处理，也是当下物理教学的一个重要方面——培养学生用数学语言描述物理过程，用数学方法处理物理问题的相关能力。但是引导学生用此类方法进行处理时，依然要和学生结合函数关系分析出具体的物理情境，不能简单地将物理问题数学化。

2有关时间的临界问题

高一阶段常常会涉及到最短时间的问题，行程类问题和小船渡河问题中都涉及到最短时间的问题。

例2 有一汽车沿着平直的公路从甲地静止出发驶向相距为s的乙地，已知汽车先做匀加速直线运动，加速度为a₁，接着做匀速运动，最后做匀减速直线运动停于乙地，加速度为a₂，那么，该汽车从甲地运动到乙地最短时间是多少？

分析

对于运动学问题，很多学生会想到建立方程组进行求解，其实利用图象研究物理问题也是一种常用的数学方法，借助于图象简单、直观等优点帮助学生分析物理过程，找到问题中涉及到的临界条件，接着再计算得出结论。本题做出汽车的v-t图象如图2所示，四边形OABC的面积表示甲乙两地的距离s，动态作图，为了保证面积不变，可以发现改变加速时间会导致总时间的变化，继而找到临界，即先加速接着减速时间最短。

3有关摩擦力的临界问题

高中阶段的摩擦力主要是两类：静摩擦力和滑动摩擦力。其中静摩擦力具有应变性以及一定的取值范围；而滑动摩擦力的产生条件是发生摩擦的两个物体之间要存在相对滑动。当物体的运动状态和受力情形发生变化的时候，就可能导致静摩擦力或滑动摩擦力发生变化，自然也就有对应摩擦力临界状态的发生。传送带模型经常与此类问题结合在一起成为问题设计的情境。

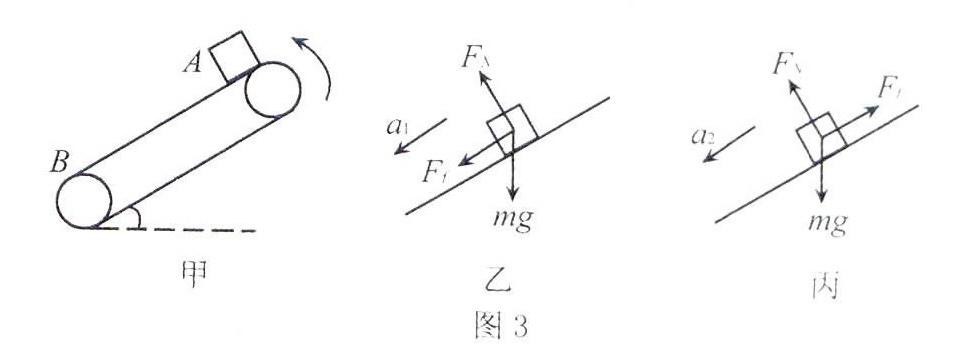
例3 一个如图3中甲图所示的倾斜传送带长度为16 m。其倾角为37°，现在正以10 m/s的速度逆时针匀速运转。某质量为0.5kg的物体从其上端由静止状态释放，已知物体与传送带之间的动摩擦因数为0.5，求物体从上端A运动到底端B所需要的时间。

分析 本题的解题关键在于学生要能分析出物体下滑16m过程中的运动状态，具体操作如下：

①对初始状态的物体进行受力分析，除重力和支持力之外，考虑到初阶段物体即使要加速，其开始阶段的速度也要小于传送带的速度，亦即物体相对于传送带有向上的速度，则滑动摩擦力向下，完整受力如图3中的乙图所示：

②第一阶段受力情形会一直持续到物体的速度增加到与传送带速度相等的10 m/s，其后有一个判断，物体在这段时间内加速的位移为多少。通过计算可得，这一阶段加速时间为1s，对应位移5 m，即尚有11 m的位移需在第二阶段走完。

③第二阶段的受力是何特点呢？考虑到物体速度已经达到与传送带一致，则有两种可能，可能随传送带一起匀速下降，也可能继续加速。但由于最大静摩擦力小于重力沿斜面方向分量，即物体的静摩擦力无法抗衡重力的影响，物体会继续加速，而其速度一旦大于传送带速度，则其滑动摩擦力会沿斜面向上，受力情况如图3中丙图所示，结合第二阶段的加速度求解和剩余位移11 m的已知，可求出第二段时间也为1 s，则全段时间2 s。

进一步的思考：本题涉及到的临界状态在于物体与传送带速度相等的时刻，这一时刻是物体运动形式切换的分界点。如果本题中的动摩擦因数较大，大于或等于传送带倾角的正切值，物体会匀速下滑；而如果动摩擦因数小于倾角的正切值，则与本题所出现的情形一致，物块继续加速，但是要区分前后阶段滑动摩擦力方向上的差别。此外这也体现了滑动摩擦力作用上的区分：前阶段滑动摩擦力充当动力；后阶段滑动摩擦力起到阻力的效果。

4有关弹力的临界问题

弹力也属于应变力，而且其方向都有严格的限制。例如，绳子的力就只能沿其收缩的方向；支撑面上的力肯定是垂直于表面向外的推力。当外界的影响达到一定程度，使得绳子或支撑面上的力逐渐减小到零之后，这些地方的力是不会出现为负值的，因为矢量的正负往往具有方向的含义，即它们的力不会反向：绳子不可能起到支撑作用；支撑面也不会反过来进行吸附。此类情况经常出现在竖直平面里圆周运动的相关问题中一

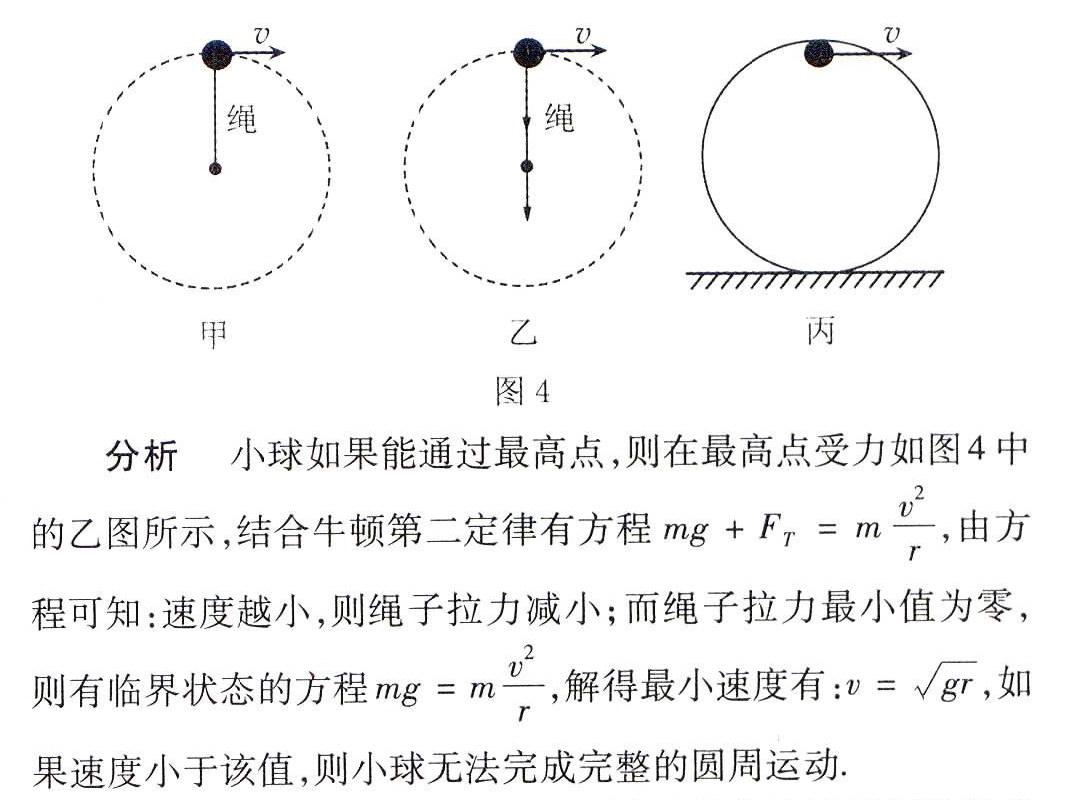
例4 绳子拉动的小球在竖直平面里做半径为r的圆周运动，如图4中的甲图所示。求进行完整的圆周运动对小球通过最高点的速度有何要求。（自由落体运动加速度为g）

进一步的思考：本例题还可以用水流星作为情境创设的背景，得出最高点速度的范围。此外如果是如图4中丙图的圆形轨道模型，在最高点提供给小球的力类似于绳子，只能提供往下的力，而不能提供向上的力，因此，临界状态与上述情形完全一致。

综上所述，教师引导学生对临界问题进行处理时，不应该将学生的视线束缚在临界状态这一点上，而应该结合过程进行动态的分析，思考临界情形发生的根源，这才有助于学生能力的真正提高。当然，从方法上看，求解这类问题较多用到数学方法，在分析清楚了过程和临界条件的基础上运用数学知识解决物理极值问题，不仅易被高中学生接受，而且能培养学生处理信息和应用数学知识解决物理问题的能力。