基于非理想CSI的下行MU-MIMO鲁棒波束成形
2016-11-25李瑜锋
曹 杰,廖 勇,王 丹,周 昕,李瑜锋
(1.重庆大学飞行器测控与通信教育部重点实验室,重庆 400044;2.西安电子科技大学综合业务网理论及关键技术国家重点实验室,陕西西安 710071;3.重庆邮电大学通信与信息工程学院,重庆 400065)
基于非理想CSI的下行MU-MIMO鲁棒波束成形
曹 杰1,2,廖 勇1,2,王 丹3,周 昕1,李瑜锋1
(1.重庆大学飞行器测控与通信教育部重点实验室,重庆 400044;2.西安电子科技大学综合业务网理论及关键技术国家重点实验室,陕西西安 710071;3.重庆邮电大学通信与信息工程学院,重庆 400065)
在下行多用户多入多出(MU-MIMO)系统中,基站(BS)所获得的非理想信道状态信息(CSI)会导致频分双工(FDD)系统预编码性能变差.现有的MU-MIMO鲁棒预编码算法虽然可以对抗非理想CSI所导致的系统性能损失,但其只考虑其中一种或两种信道误差的鲁棒性,因此系统性能提升有限.本文通过建立包含信道估计误差、量化误差和延时误差的联合信道误差模型,推导出具有集中式特性的基于最小均方误差(MMSE)的鲁棒波束成形矩阵的闭式解;随后将这种信道条件应用到分布式通信系统,并推导出具有分布式特性的基于信号泄露的MMSE的鲁棒波束成形矩阵的闭式解.数值分析表明,本文所提的集中式和分布式MU-MIMO波束成形算法,与只考虑量化误差的鲁棒MMSE算法相比,具有更优的系统和速率与误码率,补偿了上述三种信道误差所导致的预编码性能损失.
多用户多入多出;信道状态信息;频分双工;信道误差;波束成形;最小均方误差
1 引言
多入多出(Multiple Input Multiple Output,MIMO)技术能够有效提升频谱效率和传输速率,已经被大量应用在现代通信系统中,如多用户通信系统等.多用户MIMO(Multiuser MIMO,MU-MIMO)下行系统中基站(Base Sta-tion,BS)在同一时频资源上与多个用户进行通信,用户不可避免地将受到多用户干扰.为了消除这种干扰,通常选择在BS端进行波束成形.
早期波束成形算法假设BS能够获得理想信道状态信息(Channel State Information,CSI).但是在实际通信应用中,BS无法获得理想CSI:如在时分双工(Time Division Duplexing,TDD)系统中,BS可以根据上下行链路的互易性,通过上行信道进行信道估计获得CSI,但是由于估计的不准确性,会导致信道估计误差;而在频分双工(Frequency Division Duplexing,FDD)系统中,BS一般通过用户端的信道估计和有限反馈的方式获得CSI,但有限反馈会导致量化误差,且信道反馈过程会带来延时误差.因此非理想CSI下的多用户下行鲁棒波束成形设计成为了研究热点[1,2].
文献[3]研究了非理想CSI下的下行多用户多入单出(Multiple Input Single Output,MISO)系统中的鲁棒最小均方误差(Minimum Mean Square Error,MMSE)波束成形问题,但是其只考虑了信道量化误差;文献[4]扩展了非理想CSI信道误差模型,考虑了信道量化和延时误差同时存在的情况,提出了针对这两种误差的鲁棒MMSE波束成形算法;但上述算法均只适用于MISO系统,并不适用于用户多天线的情况,具有一定的局限性.文献[5]针对用户多天线环境,提出了针对信道量化误差的下行多用户认知MIMO鲁棒MMSE预编码算法;文献[6]研究了延时和估计误差存在下的下行MU-MIMO鲁棒MMSE波束成形设计.而实际上基于FDD的MU-MIMO通信系统中,BS获得的CSI同时存在估计、量化和延时误差.因此,本文考虑FDD下,在估计、量化和延时误差同时存在下的下行MU-MIMO鲁棒波束成形问题.
本文研究了非理想CSI下的下行MU-MIMO鲁棒波束成形设计,主要贡献在于:(1)建立MU-MIMO系统中,包含信道估计、量化和延时误差的联合信道误差模型;(2)推导基于BS发射功率约束下的MMSE鲁棒波束成形解,该波束成形针对三种信道误差均具有鲁棒性;(3)提出一种基于信号泄露的MMSE鲁棒波束成形设计,并给出求解算法.
2 系统模型
考虑下行MU-MIMO系统,BS在同一时频资源上为K个用户服务,BS配置M根发送天线,每个用户配置N根接收天线.假设从BS到用户k的信道矩阵用M×N的矩阵Gk表示,其元素相互独立且为零均值、单位方差的复高斯随机变量.令W和x分别为M×KN的预编码矩阵和KN×1的发送信号向量.第k个用户接收到的信号可以表示为:
(1)
其中,nk表示用户k所接收到的加性高斯白噪声的N×1向量,其元素相互独立且为零均值、单位方差的复高斯随机变量,(·)H表示矩阵的共轭转置.所有K个用户接收到的信号为:
y=GWx+n
(2)

BS和用户间CSI与信号传输过程如图1所示,主要分为三个步骤:(1)BS向用户发送信道训练序列;(2)用户接收训练序列并进行信道估计,对信道估计矩阵进行量化,通过有限反馈向BS发送信道量化矩阵;(3)BS获得信道量化矩阵,根据所获得CSI设置预编码矩阵,并向用户传输数据.上述估计、量化、反馈的过程分别会带来信道估计、量化和延时误差,BS基于这种非理想CSI,确定预编码矩阵W,并向K个用户同时发送信号.

3 信道误差模型
为了设计同时存在信道估计、量化和延迟误差下的鲁棒性下行MU-MIMO波束成形,需要建立尽可能逼近真实信道的信道误差模型,本节我们将在分析上述三种信道误差模型的基础上,提出联合信道误差模型.
3.1 估计信道误差模型
假设Hk为用户k对原始信道矩阵Gk进行信道估计后得到的估计信道矩阵,有以下信道估计模型[7]:
Gk=Hk+Δk
(3)

3.2 量化信道误差模型

(4)
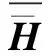
(5)
3.3 延时信道误差模型
延时信道误差建模采用平稳遍历高斯马尔科夫块衰落方法[9],表示如下:
Hk[n]=ρkHk[n-1]+Ek[n]
(6)
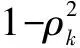
3.4 联合信道误差模型
在信道估计、量化和延时误差同时存在的情况下,根据式(3)、(5)和(6),第n个时刻BS到用户k的信道矩阵Gk[n]建模为:

+Ek[n]+Δk[n-1]
(7)
将式(7)写成矩阵形式,假设G=(G1,…,GK)H,得到:

(8)
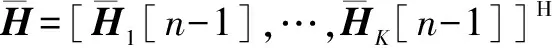
E=[E1[n],…,EK[n]]H,
D=diag(ρ1,…,ρK),


A=DΛC,B=DΛZ,diag(·)表示对角矩阵.
4 集中式波束成形设计
基于有限反馈的传统波束成形设计中,一般直接将量化的CSI代替真实的CSI用于波束成形设计[10],并没有考虑补偿量化误差对系统性能的影响,在量化误差环境下性能较差;或者只是考虑某两项误差因素,如量化和延时误差[4]或延时和估计误差[11]下的鲁棒波束成形算法.本节所提算法充分考虑信道量化、延时和估计三个因素对波束成形矩阵的影响,根据MMSE准则设计波束成形矩阵,以期获得更好的鲁棒性.

(9)

minε(W,β)
s.t. tr(WWH)≤P
(10)
上述设计不具有鲁棒性,只适用于理想CSI环境中.将MSE的条件期望作为优化函数,根据联合信道误差模型,集中式鲁棒波束成形设计为:
s.t. tr(WWH)≤P
(11)
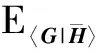
+KN
=μ(W,β)
(12)
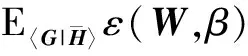
问题式(11)为凸优化问题,其全局最优解能够通过KKT(Karush-Kuhn-Tucker)条件获得[12].采用拉格朗日算子法解决式(12)提出的凸优化问题,拉格朗日函数表示为:
l (W,β,λ)=μ(W,β)+λ[tr(WWH)-P]
(13)
其中,λ为拉格朗日算子.假设最优波束成形矩阵为W*,β的最优解为β*,分别对W,β求一阶导数,根据KKT条件,最优解处对应的一阶导数为零,即:
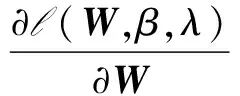
=0
(14)
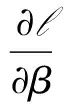
=0
(15)
由式(14)可以得到:
(16)
由式(16)可知,若λβ2已知,即可获得W的闭式解.为了求出λβ2,将式(15)进一步化简如下:
(17)
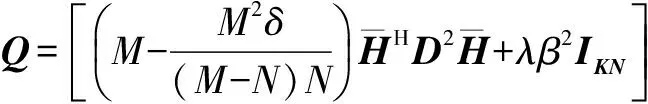
(18)
对式(17)的左边化简,并且将式(18)代入可以得到:
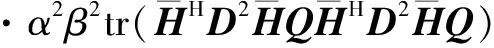
=λβ2·tr(WWH)
=λβ2P
(19)
由式(17)、(19)得:
(20)
将式(20)代入式(16),波束成形矩阵表示为:

(21)

(22)
至此,集中式系统最优的波束成形矩阵为:
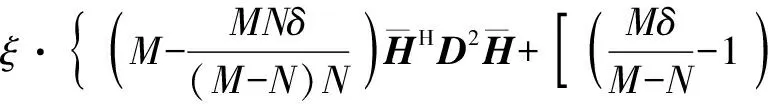
(23)
5 分布式波束成形设计
第4节分析了基于MMSE的下行MU-MIMO鲁棒波束成形设计,其综合考虑了信道估计、量化和延时误差三种因素的影响,但其只适用于集中式通信系统,这不便于BS实际应用.本节将其推广到偏向于实用的分布式波束成形设计,即BS为每个用户单独设计预编码矩阵.为此,本节定义了基于信号泄露的MMSE表达式,并且考虑BS所获得的CSI存在信道估计、量化和延时误差的情况,推导出具有鲁棒性的分布式波束成形的闭式解.
将式(1)写成如下形式:
(24)
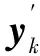

(25)
由此,我们得到基于信号泄露的MMSE鲁棒波束成形设计问题:

(26)

(27)
文献[13]阐述了基于信号泄露的MMSE表达式为凸函数,因此问题(26)为凸优化问题,可以用KKT条件求解,构建式(26)的拉格朗日函数如下:
(28)
式(28)中的l (Wk,β,λk)对Wk,β分别求偏导数:
=0
(29)
=0
(30)
根据式(29),可以得到用户k的波束成形矩阵Wk:
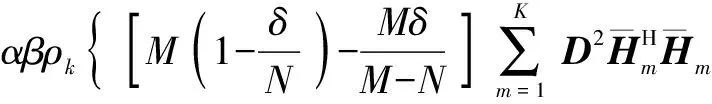
(31)
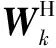

=0
(32)
(33)
将式(33)代入式(31)得到:
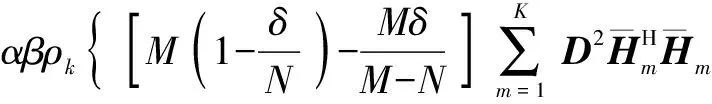
(34)
为了求得β,令
(35)

(36)
因此分布式系统最优波束成形矩阵为:
(37)
其中

(38)
6 数值分析

首先我们仿真了上述5种算法的系统和速率性能.系统和速率可由下式得到:
(39)
图2设定延时归一化参数fdTs=0.1、估计误差σ2=0.1、反馈比特数B=16bit,给出了系统和速率与信噪比(Signal to Noise Ratio,SNR)的关系.可以看出:(1)算法1和算法2明显优于鲁棒MMSE,并能够克服MMSE在高SNR下性能下降的问题.这是因为算法1和算法2考虑补偿三种误差,而鲁棒MMSE只补偿了量化误差,MMSE和BD算法无鲁棒性,在同样的SNR条件下,本文所提两种算法比鲁棒MMSE、MMSE和BD算法,经过波束成形后,用户接收到的残留干扰更小,信干噪比(Signal to Interference Plus Noise Ratio,SINR)更大,因此系统和速率更高;(2)算法2的系统和速率比算法1稍差.这是因为,算法2虽然也考虑了补偿三种误差,但是其不是所有用户总均方误差最小算法,因此其系统和速率比算法1稍差.

表1 主要仿真参数


图3给出了误码率(Bit Error Rate,BER)性能与反馈比特数的关系.设定延时归一化参数fdTs=0、估计误差σ2=0.可以看出,在仅存在信道量化误差的应用场景中,算法2的BER比算法1稍差,鲁棒MMSE算法的BER和算法1近似相同,都明显优于MMSE和BD算法.其原因是,BS获知的CSI存在量化误差,若没有对量化误差进行相应补偿,BER增加.
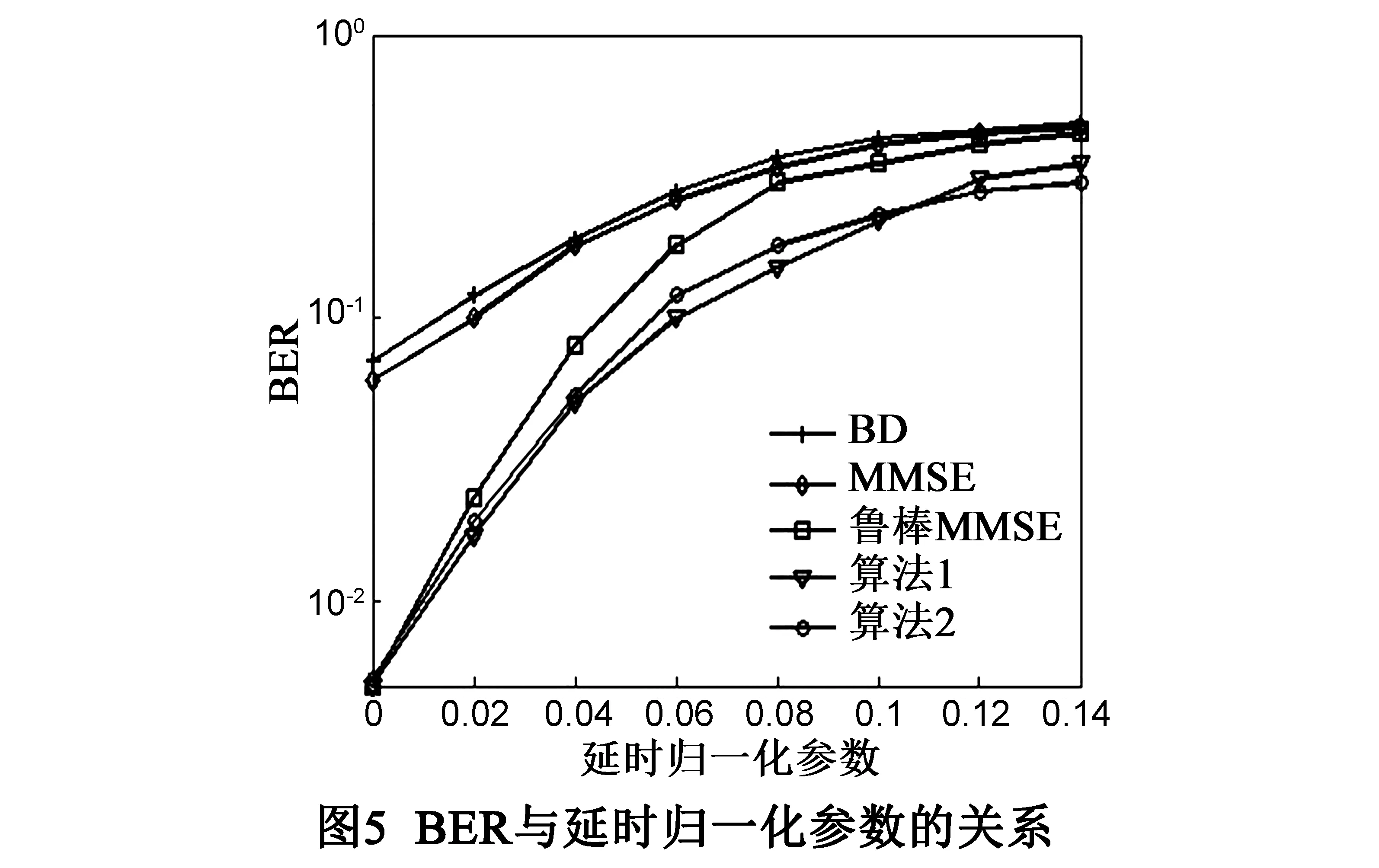
图4给出了反馈比特数B=18bit、fdTs=0时的BER与估计误差的关系.不难得到:随着估计误差增加,算法1和算法2的BER上升平缓,鲁棒MMSE误码率性能恶化快,但是稍优于MMSE和BD算法.其原因是:当估计误差小时,反馈比特数占主导因素,因此算法1、算法2和鲁棒MMSE算法的BER性能优于MMSE和BD算法;随着估计误差增大,对估计误差无鲁棒性的波束成形算法,残留干扰增多,SINR增加,BER性能恶化严重,因此算法1和算法2的BER性能优于其它三种算法.图5仿真比较了σ2=0、B=18bit时,系统BER与延时的变化关系.由图5可知:延时增大,BER性能下降严重;在相同的延时情况下本文所提算法的BER性能优于其它算法.其原因是:信道延时增加,信道相关性增强,信道准确性下降严重,因此干扰残留功率增大,造成BER下降;而此时考虑了延时的鲁棒性波束成形设计,能够提高BER性能.

7 结束语
本文研究了非理想CSI下的下行MU-MIMO鲁棒波束成形设计.首先根据FDD系统实际存在的信道估计、量化和延时误差,建立了联合信道误差模型,并在此模型基础上提出基于MMSE的集中式鲁棒波束成形设计;然后定义了一种基于信号泄露的MMSE的分布式鲁棒波束成形设计,并求得波束成形矩阵的闭式解.数值结果表明在非理想CSI环境中,本文所提两种算法比传统MMSE算法性能更优;相对而言,分布式波束成形算法比集中式波束成形算法性能稍差,但是其能为单个移动用户独立设置波束成形矩阵,适用于更为实用的分布式通信系统.
[1]孙昕,张钦,马鹏飞.一种下行多用户MIMO系统中的鲁棒波束形成算法[J].电子学报,2009,37(3):444-448.SUN Xin,Zhang Qin,Ma Peng-fei.An algorithm of robust beamforming in the downlink multiuser MIMO system[J].Acta Electronica Sinica,2009,37(3):444-448.(in Chinese)
[2]LI C G,YANG L X,ZHANG W P.A two-way MIMO relaying scheme with partial channel state information[J].Wireless Personal Communications,2013,72(4):1949-1968.
[3]ZHANG C H,XU W,CHEN M.Robust MMSE beamforming for multiuser MISO systems with limited feedback[J].IEEE Signal Processing Letters,2009,16(7):588-591.
[4]DAI B B,XU W,ZHAO C M.Optimal MMSE beamforming for multiuser downlink with delayed CSI feedback using codebooks[A].Global Telecommunications Conference[C].Houston,USA:IEEE,2011.1-5.
[5]GUI X,KANG G X,ZHANG P.Linear precoding design in multi-user cognitive MIMO systems with cooperative feedback[J].IEEE Communications Letters,2012,16(10):1580-1583.
[6]ZHANG Q,HE C,JIANG L,et al.Robust per-stream MSE based transceiver design for MIMO interference channel[A].Global Telecommunications Conference[C].Atlanta,GA:IEEE,2013.3990-3995.
[7]CHUNG P J,DU H Q,GONDZION J.A probabilistic constraint approach for robust transmit beamforming with imperfect channel information[J].IEEE Transactions on Signal Processing,2011,59(6):2773-3782.
[8]RAVINDRAN N,JINDAl N.Limited feedback-based block diagonalization for the MIMO broadcast channel[J].IEEE Journal on Selected Areas in Communications,2008,26(8):1473-1482.
[9]ZHANG J,KOUNTOURIS M,ANDREWS G,et al.Multi-mode transmission for the MIMO broadcast channel with imperfect channel state information[J].IEEE Transactions on Communications,2011,59(3):803-814.
[10]LEE N,SHIN W.Adaptive feedback scheme onK-cell MISO interfering broadcast channel with limited feedback[J].IEEE Transactions on Wireless Communications,2011,10(2):401-406.
[11]XU Y S,HE C,LI J.A robust AMSE-minimization game in multicell multiuser wireless system[A].Global Telecommunications Conference[C].Atlanta,GA:IEEE,2013.4175-4180.
[12]OH D,LEE H,LEE Y.Power control and beamforming for femtocells in the presence of channel uncertainty[J].IEEE Transactions on Vehicular Technology,2011,60(6):2545-2554.
[13]SUN F,CARVALHO D.A leakage-based MMSE beamforming design for a MIMO interference channel[J].IEEE Signal Processing Letters,2012,19(6):368-371.
[14]SHEN H,LI B,TAO M X,et al.MSE-based transceiver designs for the MIMO interference channel[J].IEEE Transactions on Wireless Communications,2010,11(9):3480-3489.

曹 杰 男,1990年出生于江西省九江市.重庆大学飞行器测控与通信教育部重点实验室硕士研究生.主要从事下行MIMO预编码、多小区协作等领域研究.
E-mail:cjnanchangedu@126.com

廖 勇 男,1982年出生于四川省自贡市.2014年毕业于重庆大学,获博士学位,现为该校副研究员,从事宽带无线网络通信、飞行器测控与通信等领域研究工作.
E-mail:liaoy@cqu.edu.cn
Robust Beamforming for Downlink MU-MIMOBased on Imperfect CSI
CAO Jie1,2,LIAO Yong1,2,WANG Dan2,ZHOU Xin1,LI Yu-feng1
(1.KeyLaboratoryofAerocraftTT&CandCommunication,MinistryofEducation,ChongqingUniversity,Chongqing400044,China;2.TheStateKeyLaboratoryofIntegratedServicesNetworks,XidianUniversity,Xi’an,Shaanxi710071,China;3.SchoolofCommunicationandInformationEngineering,ChongqingUniversityofPostsandTelecommunications,Chongqing400065,China)
The channel state information (CSI) at base station (BS),obtained from users in the multiuser multiple input multiple output (MU-MIMO) system,leads to precoding performance degradation in frequency division duplexing (FDD) system.Existing robust beamforming precoding algorithms in MU-MIMO can reduce the performance loss caused by imperfect CSI.However,these algorithms only take one or two robustness channel errors into consideration,as a consequence,the system performance is limited to be improved.By establishing joint channel error model including channel estimation error,quantization error and delay error,we derive the closed-form solution of robust beamforming matrix based on minimum mean square error (MMSE).And then,we derive the closed-form solution of robust beamforming matrix based on MMSE of signal leakage with distributed characteristics while applying to distributed communication system.When compared to the traditional MMSE algorithm which only considers quantization error,numerical analysis shows that,the proposed centralized and distributed downlink MU-MIMO beamforming algorithms have better sum rate and bit error rate (BER),and reduce the precoding performance loss caused by the above three channel errors.
multiuser multiple input multiple output;channel state information;frequency division duplexing;channel error;beamforming;minimum mean square error
2015-01-12;
2015-06-09;责任编辑:覃怀银
国家自然科学基金(No.61501066);重庆市前沿与应用基础研究计划项目(No.cstc2015jcyjA40003);西安电子科技大学综合业务网理论及关键技术国家重点实验室开放基金(No.ISN16-03);中央高校基本科研业务费重点基金(No.CDJZR165505)
TN925.5
A
0372-2112 (2016)09-2093-07
��学报URL:http://www.ejournal.org.cn
10.3969/j.issn.0372-2112.2016.09.011
