基于多任务贝叶斯压缩感知的稀疏可重构天线阵的优化设计

沈海鸥,王布宏,李龙军

(空军工程大学信息与导航学院,陕西西安 710077)



基于多任务贝叶斯压缩感知的稀疏可重构天线阵的优化设计

沈海鸥,王布宏,李龙军

(空军工程大学信息与导航学院,陕西西安 710077)

建立方向图可重构天线的联合稀疏模型，基于多任务贝叶斯压缩感知理论提出一种稀疏可重构天线阵的优化设计方法.该方法在实现方向图精确重构的同时可以大幅减少天线数量，节省平台空间，降低设计成本.首先基于多任务贝叶斯压缩感知理论建立多目标方向图的稀疏优化模型，根据权值向量的先验概率分布，利用快速相关向量机估计超参数的最大后验概率来得到多组阵元位置及其激励，实时改变激励以获得不同方向图的稀疏逼近.仿真验证了该方法能够以较少的阵元个数和较高的方向图拟合精度快速实现方向图重构.

稀疏布阵；方向图可重构天线；多任务贝叶斯压缩感知；相关向量机

1 引言

近年来，阵列天线已经广泛应用于雷达、通信电子系统中，为应对多功能、多任务的需求，天线的数量和复杂程度大幅增加，对有限的平台空间和载荷、天线布局、成本、电磁兼容控制等问题提出了严峻的挑战.可重构天线[1～3]的发展应用为解决上述问题提供了有效的思路，它能够在同一天线孔径上实时改变某些结构完成天线性能的重构，通过切换天线的不同工作状态实现多个天线的功能.方向图可重构天线[2，3]作为一种重要的可重构天线，因其具有实时重构天线辐射方向图的特性而在现代超宽带、大容量、多功能集成信息系统中发挥着重大作用.以往的研究主要集中在改变辐射体的内在结构[4]或引入寄生辐射体[5]来实现方向图可重构，这种方式会增加天线单元的设计难度，不适合辐射体较小的情况.近些年，国内外学者在改变馈电结构[6～8]方面也研究取得了重要进展，如文献[9～12]提到的唯相位法，仅通过改变馈电相位的分布来实现不同方向图的控制，通常采用交替投影技术[9]或优化算法[10～12]来实现，因为非凸集的引入和目标函数的非线性约束使得交替投影法容易陷入局部最优解，而优化算法大大增加了计算复杂度.以上方法都采用简单的均匀布阵方式，并没有考虑阵元数量对多功能天线成本、性能的影响.非均匀稀疏布阵具有分辨力高，互耦效应利于抑制，成本低等优点，它在最小化旁瓣电平方面取得了一定研究成果[13～15]，但是由于稀布阵的波束赋形涉及较多的未知参数，使其在实现多方向图重构方面少有涉及.同时，现有方向图重构的目标通常仅仅对主瓣宽度和副瓣峰值电平等性能指标进行优化约束，而对天线方向图的精确赋形鲜有报道.综合上述分析，如何在同一孔径上快速有效地选择尽可能少的天线单元及相应激励，精确实现方向图可重构天线阵还有待深入研究.

伴随稀疏信号理论的发展，贝叶斯压缩感知(BCS，Bayesian Compressed Sensing)[16，17]在稀疏性、灵活性、精度等方面的优势使其具有重要的研究价值，由于BCS的有效性不依赖于矩阵的约束等距性，且不同的先验概率分布对应不同的重构算法，单任务BCS已被成功用于解决单个方向图的稀疏综合问题[18，19].但是当期望方向图非对称，激励为复数时，BCS只能得到仅有实部或仅有虚部的激励，效果并不理想.另外，如果利用该方法实现方向图可重构天线的稀疏优化，每一种方向图的拟合对应一个独立的单任务BCS，使得所需的布阵位置不同，很有可能导致阵元间距过小而无法工程实现，适用范围受限.同样被这一因素限制的还有矩阵束方法[20，21]和欠定系统局域解法[22].与此同时，分布式压缩感知[23，24]及多任务贝叶斯压缩感知[25，26]理论提到的“联合稀疏重构”概念对于解决上述问题具有指导意义.本文将方向图可重构天线设计建模为多任务联合稀疏重构，基于MT-BCS建立多目标方向图的稀疏优化模型，在同一孔径下通过选择尽可能少的阵元位置及其激励实现了不同方向图的稀疏逼近.现将本文主要工作归纳如下：

(1)通过详细分析方向图可重构天线的采样矩阵形式，使表征天线单元位置和激励大小的多组权值向量满足相同的先验概率分布，建立可重构线阵设计的联合稀疏模型.

(2)基于MT-BCS理论，在同一孔径下利用快速相关向量机估计超参数的最大后验概率，通过求解最稀疏的权值向量以获得不同方向图的稀疏逼近.

(3)文中对输入参数的选择和方向图重构性能进行了详细的仿真分析，验证了算法在阵列设计稀疏率、方向图精确拟合及其联合优化效率上的优越性.

2 基于MT-BCS的方向图可重构稀疏天线阵优化设计

假设长为L的天线孔径可以均匀分为N个阵元位置栅格，通过选择阵元位置，改变馈电电流可设计出可重构天线的M种工作状态，即产生M种不同的方向图.综合可得天线阵的第m种方向图：

(1)

对以上M种方向图进行Km(Km≪N)点采样可得其矩阵形式：

F(m)=Φ(m)w(m),m=1,…,M

(2)

Φ(m)

(3)

(4)

(5)

将矩阵表达式(5)的各项按实部和虚部展开得：

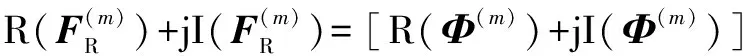
·[R(w(m))+jI(w(m))]+[R(e(m))+jI(e(m))]

=[R(Φ(m))R(w(m))-I(Φ(m))I(w(m))+R(e(m))]

+j[I(Φ(m))R(w(m))+R(Φ(m))I(w(m))

+I(e(m))]

(6)

(7)

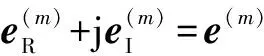
(8)

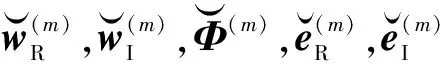
(9)

(10)

即满足：

(11)

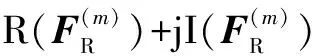
=[R(Φ(m))+jI(Φ(m))]·w(m)+[R(e(m))+jI(e(m))]

=[R(Φ(m))w(m)+R(e(m))]+j[I(Φ(m))w(m)

+I(e(m))]

(12)

有：

(13)

写成矩阵形式为：

(14)

(16)

(17)

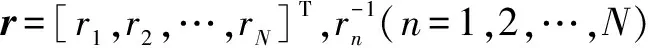
(18)

(19)

(20)

(21)

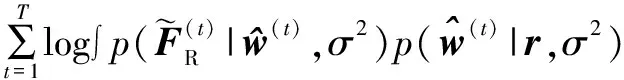
(23)

且有：

(24)

(25)

综上，给出方向图可重构稀疏线阵的实现步骤：

Step 5 参数输出.输出方向图可重构天线的实际阵元个数P及每种方向图对应的激励w(m).

3 仿真结果及分析

在实现方向图可重构天线的目标要求下，为了验证本文算法在阵元个数、拟合精度、计算时间方面的优势，基于MT-BCS多目标方向图稀疏优化模型，给出下面几组仿真验证.

3.1 调节参数的选择

实验1 以具有两种(M=2)方向图的可重构稀疏线阵为例研究不同输入参数对算法性能的影响，仿真采用L=14.5λ(PUNI=2L/λ)的天线孔径，期望波束形状为笔形波束和平顶波束，以调节参数为横坐标，以实际阵元个数P(右)和方向图归一化均方误差ξ(左)为纵坐标得双y轴仿真图，在权衡性能指标(P≤24且ξ≤2×10-4)，固定其他参数(a=7×102、b=8×101、σ2=1×10-3、N=500、{K1,K2}={70,62})的情况下，仿真P和ξ随某一调节参数(a、b、σ2、N、{K1,K2})的变化趋势，结果如表1所示.

图1(a)和图1(b)分别给出了先验参数a、b对性能指标的影响，参数从10-2变化到104，ξ1和ξ2的变化趋势大致相同，都随着a的增加而减小，随着b的增加而增加，而P的变化恰好与ξ的变化相反，因此，为了权衡阵列稀疏性和方向图匹配准确度两项指标，先验参数的选择范围可设置为a∈[1×102,1×103]，b∈[4×101,2×102].而噪声方差σ2对性能的影响可以由图1(c)得到，当σ2<1×10-2时，阵元个数及两个方向图的均方误差均稳定在较低的范围，具有优异的性能，因此，选择σ2∈(1×10-5,1×10-2).从图1(d)中可以看出，N>1×103之后，阵元个数P由于孔径栅格数的增多不断增大，计算复杂度也随之增加，而当N∈[1×102,1×103]时，ξ和P均能保持在较理想的范围.图1(e)给出P和ξ随方向图采样点数的变化趋势，从图中可以看出，方向图均方误差随K的增大而减小，直到K大于30时，在1×10-3以下波动，因此，{K1,K2}的值可在[50,80]的范围内选择以满足可重构稀疏线阵的性能要求.

表1 调节参数的选择

3.2 具有三种方向图的可重构稀疏线阵

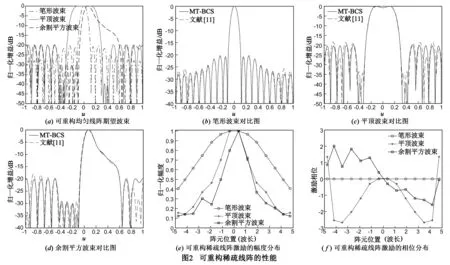
实验2 取天线孔径L=9.5λ(PUNI=20)，以可重构均匀线阵可实现的三种波束形状(笔形波束、平顶波束、余割平方波束)为期望方向图(如图2(a)所示)进行仿真实验，最大旁瓣电平设为-20dB，运算耗时1.3130s (CPU3.40GHz，3.46GBRAM，Matlab2012b).

图2(b)、(c)和(d)分别给出了本文算法与文献[11]算法重构得到的三种波束对比图，从图中可以看出，两种方法的方向图主瓣赋形区波束形状和旁瓣电平均能较好的满足设计需求，且本文方法具有更低的峰值旁瓣，对于精确赋形要求较高的应用场合，本文算法的优势更加明显，它能够实现方向图高精度拟合，能够重构出与三种期望方向图形状基本一致的波束方向图，归一化均方误差分别为9.6842×10-5、8.2149×10-5和9.5863×10-5，两种方法的方向图性能参数比较见表2.表3给出了本文可重构稀疏线阵的阵元位置分布，从表中可以看出，相比于等间隔排列的20元均匀可重构线阵，本文算法可稀疏30%的阵元，只需要14个阵元即可实现重构功能，且最小阵元间距为0.5605λ，平均阵元间距为0.7308λ.图2(e)和(f)分别给出了该稀布阵阵元激励的幅度分布和相位分布.

表2 可重构线阵方向图性能对比

表3 可重构稀疏线阵的阵元位置分布

4 结论

方向图可重构天线通过在同一天线孔径上实时改变某些结构来实现不同的天线方向图.本文结合非均匀稀疏布阵具有分辨力高，互耦效应利于抑制，成本低的优点，提出了一种方向图可重构天线的稀疏布阵方法.通过建立方向图可重构天线的联合稀疏模型，求解尽可能少的阵元和相应激励来获得不同方向图的稀疏逼近.仿真试验证明该方法能够以较少的阵元个数和较高的精度有效实现方向图重构，节省平台空间的同时大幅减少天线数量，降低载荷和成本.

[1]Haupt R L,Lanagan M.Reconfigurable antennas[J].IEEE Antennas and Propagation Magazine,2013,55(1):49-61.

[2]Kang W,Kim K.A radiation pattern-reconfigurable antenna for wireless communications[A].2011 IEEE International Symposium on Antennas and Propagation[C].Spokane,USA:IEEE Antennas and Propagation Society,2011.1545-1548.

[3]Wang B Z,Xiao S Q,Bai Y Y,Zhang G M.Researches on pattern reconfigurable antenna and its application in phase array[A].Proceeding of the 2011 International Workshop on Antenna Technology[C].HongKong,China:Agilent Technologies,2011.46-49.

[4]Kang W S,Park J A,Yoon Y J.Simple reconfigurable antenna with antenna with radiation pattern[J].IET Electronics Letters,2008,44(1):182-183.

[5]Rodriguez J A,Trastoy J C,Bregains J C,Ares F,Franceschetti G.Beam reconfiguration of linear arrays using parasitic elements[J].Electronics Letters,2006,42(3):131-133.

[6]Ding X,Wang B Z.A millimeter-wave pattern-reconfigurable antenna with a reconfigurable feeding network[J].Journal of Electromagnetic Waves and Applications,2013,27(5):649-658.

[7]Manica L,Rocca P,Martini A,Massa A.An innovative approach based on a tree-searching algorithm for the optimal matching of independently optimum sum and difference excitations[J].IEEE Transactions on Antenna and Propagation,2008,56(1):58-66.

[8]Folgueiras M A,Gonzalez A R,Pena F A.Optimal compromise among sum and difference patterns in monopulse antennas:use of subarrays and distributions with common aperture tail[J].Journal of Electromagnetic Waves and Applications,2009,23(17-18):2301-2311.

[9]Vescovo R.Reconfigurability and beam scanning with phase-only control for antenna arrays[J].IEEE Transactions on Antenna and Propagation,2008,56(6):1555-1565.

[10]Isernia T,Massa A,Morabito A F,Rocca P.On the optimal synthesis of phase-only reconfigurable antenna arrays[A].Proceedings of the 5th Conference on Antennas and Propagation (EuCAP)[C].Rome,Italy:IEEE Antennas and Propagation Society,2011.2074-2077.

[11]Morabito A F,Massa A,Rocca P,Isernia T.An effective approach to the synthesis of phase-only reconfigurable linear arrays[J].IEEE Transactions on Antenna and Propagation,2012,60(8):3622-3631.

[12]Mahanti G K,Chakraborty A,Das S.Phase-only and amplitude-phase-only synthesis of dual-beam pattern linear antenna arrays using floating-point genetic algorithms[J].Progress in Electromagnetics Research,2007,68:247-259.

[13]侯青松,郭英,王布宏,王永良.基于格理论的非均匀稀疏线阵旁瓣结构的分析方法[J].电子学报,2010,38(6):1459-1463.

Hou Qing-song,Guo Ying,Wang Bu-hong,Wang Yong-liang.Analysis of side lobe structure of nonuniform sparse linear array based on lattice theory[J].Acta Electronica Sinica,2010,38(6):1459-1463.(in Chinese)

[14]Oliveri G,Donelli M,Massa A.Linear array thinning exploiting almost difference sets[J].IEEE Transactions on Antenna and Propagation,2009,57(12):3800-3812.

[15]Sartori D,Oliveri G,Manica L,Massa A.Hybrid design of non-regular linear arrays with accurate control of the pattern sidelobes[J].IEEE Transactions on Antenna and Propagation,2013,61(12):6237-6242.

[16]Ji S,Xue Y,Carin L.Bayesian compressive sensing[J].IEEE Transactions on Signal Processing,2008,56(6):2346-2356.

[17]季云云,杨震.脉冲噪声环境下高斯稀疏信源贝叶斯压缩感知重构[J].电子学报,2013,41(2):363-370.

Ji Yun-yun,Yang Zhen.Bayesian compressed sensing for Gaussian sparse signals in the presence of impulsive noise[J].Acta Electronica Sinica,2013,41(2):363-370.(in Chinese)

[18]Oliveri G,Massa A.Bayesian compressive sampling for pattern synthesis with maximally sparse non-uniform linear arrays[J].IEEE Transactions on Antenna and Propagation,2011,59(2):467-481.

[19]Zhang W,Li L,Li F.Reducing the number of elements in linear and plannar antenna arrays with sparseness constrained optimization[J].IEEE Transactions on Antenna and Propagation,2011,59(8):3106-3111.

[20]Liu Y,Nie Z P,Liu Q H.Reducing the number of elements in a linear antenna array by the matrix pencil method[J].IEEE Transactions on Antenna and Propagation,2008,56(9):2955-2962.

[21]Liu Y,Liu Q H,Nie Z P.Reducing the number of elements in the synthesis of shaped-beam patterns by the forward-backward matrix pencil method[J].IEEE Transactions on Antenna and Propagation,2010,58(2):604-608.

[22]杨鹏,闫飞,张胜辉,杨峰.基于FOCUSS算法的稀疏阵列综合[J].电子科技大学学报,2014,43(2):203-206.

Yang Peng,Yan Fei,Zhang Sheng-hui,Yang-feng.Sparse array synthesis based on FOCUSS algorithm[J].Journal of University of Electronic Science and technology of China,2014,43(2):203-206.(in Chinese)

[23]Baron D,Duarte M F,Wakin M B,Sarvotham S,Baraniuk R G.Distributed Compressive Sensing[R].USA:Department of Electrical Engineering,Technion,2009.1-43.

[24]Sundman D,Chatterjee S,Skoglund M.A greedy pursuit algorithm for distributed compressive sensing[A].International Conference on Acoustics,Speech,and Signal Processing (ICASSP)[C].Kyoto,Japan:Inst Electr Electron Eng Signal Process Soc,2012.2729-2732.

[25]Ji S,Dunson D,Carin L.Multitask compressive sensing[J].IEEE Transactions on Signal Processing,2009,57(1):92-106.

[26]Viani F,Poli L,Oliveri G,Robol F,Massa A.Sparse scatterers imaging through approximated multitask compressive sensing strategies[J].Microwave and Optical Technology Letters,2013,55(7):1553-1558.

[27]Tipping M E,Faul A C.Fast marginal likelihood maximization for sparse Bayesian models[A].Proceedings of 9th International Workshop Artificial Intelligence and Statistics[C].Key West,FL:Mike Tipping,2003.1-13.

沈海鸥 女，1990年7月出生于甘肃省兰州市，现为空军工程大学信息与导航学院博士研究生，主要研究方向为阵列信号处理和雷达信号处理.

E-mail:haioushen1990@sina.com

王布宏 男，1975年12月出生于山西省太原市，现为空军工程大学教授、博士生导师，主要从事阵列信号处理、阵列校正等方面的研究工作.

E-mail:wbhyl@aliyun.com

Optimal Design of Sparse Reconfigurable Antenna Array Based on Multitask Bayesian Compressed Sensing

SHEN Hai-ou,WANG Bu-hong,LI Long-jun

(SchoolofInformationandNavigation,AirForceEngineeringUniversity,Xi’an,Shaanxi710077,China)

In light of the equivalent joint sparse learning model,an effective method based on multitask Bayesian compressed sensing (MT-BCS) is presented for the design of pattern reconfigurable antenna arrays.The method can dynamically reconfigure arbitrary radiation patterns with the exact pattern details and as fewer number of antenna elements as possible.Firstly,the sparse learning model of multiple reference patterns is built based on MT-BCS theory and priori assumption about the priori probability of weight vectors.Then fast relevance vector machine (RVM) is exploited to estimate maximum posterior probability of hyper-parameter and further to obtain array optimizing positions and excitations.By varying excitations and optimized element positions,different patterns with desired and precise particulars can be achieved.Simulation results validate the efficiency of the proposed method for the design of maximally sparse reconfigurable antenna.

sparse array;pattern reconfigurable antenna;multitask Bayesian compressed sensing;relevance vector machine

2014-12-24;

2015-04-21;责任编辑：梅志强

国家自然科学基金资助项目(No.61172148)

TN820

A

0372-2112 (2016)09-2168-07

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.09.022