声参量阵在测风速中应用研究

宋业强，陈 敏，靳银蕊，李兴勇

（电子科技大学 航空航天学院，四川 成都 611731）

声参量阵在测风速中应用研究

宋业强，陈 敏，靳银蕊，李兴勇

（电子科技大学 航空航天学院，四川 成都 611731）

声参量阵测风速系统中的信号预处理算法的目的是生成两个具有频率差的载波信号，两信号在空气中通过非线性交互作用自解调出原信号。然后对两个传声器阵列接收到的该信号通过PHAT加权的广义互相关算法进行时延估计，得到两列信号的时间差来测得风速。通过对常用的预处理算法对音频信号进行预处理，用其在空气中自解调出来的声参量阵信号进行广义互相关算法，并对其进行MATLAB仿真分析，比较几种调制算法测得时间差的精度。经过仿真对比分析知全载波单边带调制算法预处理测得的时间差精度最高，因此全载波单边带调制算法最适合对声参量阵测风速中的信号进行预处理，在此基础上设计了声参量阵测风速系统，通过实验对比证明了声参量阵测试系统的可行性。

声参量阵；预处理算法；广义互相关法；时间差精度

声参量阵是利用声波在空气中传播时会发生非线性交互作用的特性，使用两列沿相同方向传播的超声波信号在传播过程中获得具有高指向性的低频可听声的一种声源[1]。声波频率越高在空气中衰减的越快，因此声参量阵产生的低频声波比超声波传播的距离更远，可以大大提高风速测试的空间范围，实现大空间范围的风速测试。声参量阵预处理算法的目的是对超声波换能器驱动信号的一个预处理，它对自解调出的声频信号的声压、频率、谐波失真、指向性等性能参数具有很大的影响，进而将影响到时延估计的精度。因此，选择合理的预处理算法，能够有效减小自解调信号的谐波失真，提高自解调信号的指向性，从而更加有效的传播信息。

1 基本预处理算法

1.1 双边带(DSB)算法

DSB法[2-3]是最简单的一种声频定向系统信号处理方法，其自解调信号较少受实现系统的性能影响 (如数字系统采样造成的频域混叠等)，故可以通过该方法的理论分析结果对自解调理论模型及Berktay远场解进行实验验证，双边带幅度调制算法是目前通信技术领域中较为成熟的一种调制算法，原理简单，易于实现，所以可作为预处理算法对声参量阵信号进行预处理，该算法原理框图如图1所示。

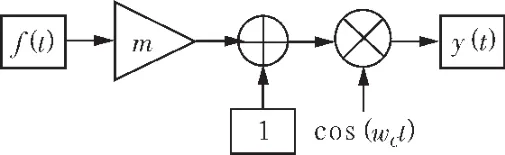
图1 双边带(DSB-AM)算法原理框图

音频信号f（t）的DSB已调制信号可以表示为：

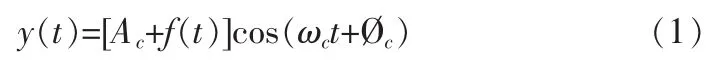
式中，Ac为载波幅度，ωc为载波频率，Øc为载波相位。为了方便描述，此处令Øc=0，当音频信号的幅度为A，即f（t）= Ag（t）时，由公式（1）可得：

其中，m=A/Ac为调制系数，Et=[1+mg（t）]Ac为已调信号的包络。

1.2 平方根法

由“Berktay远场解”[5]及自解调理论模型可知，在空气中发生非线性效应自解调出的音频信号的声压与已调制信号包络平方的二次时间导数成正比。因此，对原信号最直接的预处理方法是令调制信号的包络为，则输入的原波信号的声压公式为

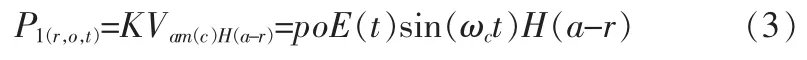
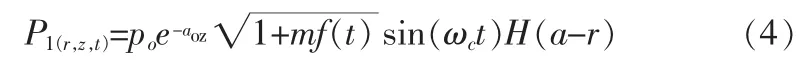
空气中自解调出的信号和原来的输入信号频率相同，没有出现其他的谐波成分，因此，在单频输入情况下，采用平方根法对信号进行预处理时得到的自解调信号不存在各种失真。

1.3 全载波单边带（SSB）算法

DSB调制算法存在效率低，带宽要求大，谐波失真大以及对后续功率放大器和超声换能器要求高等缺点。为了克服DSB算法的这些缺点，后来提出了单边带（SSB）调制算法。与DSB法相比，SSB法具有很多优点，主要表现在节约功率，节约带宽，削弱路径选择性衰落，减少噪声等方面。SSB法有抑制载波SSB法和全载波SSB法两种，但由于抑制载波SSB法不能满足无失真包络平方条件，不能作为声参量阵的预处理算法，在此不对其进行介绍，只介绍全载波 SSB法（Full carrier single sideband modulation algorithm）。目前，SSB法主要有韦弗法和希尔伯特变换法（Hilbert）两种实现方法，在此采用希尔伯特变换法[6]。其实现原理如图2所示。

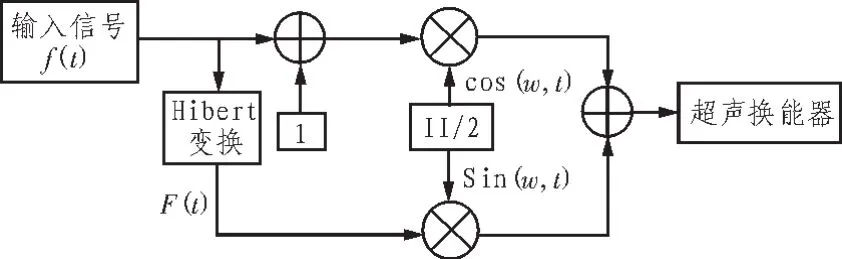
图2 单边带调制实现框图

图2 中F（t）为输入信号f（t）的Hilbert变换，sinωct和cosωct为一对正交的超声波载波，上下两路信号通过相加减分别得到下边带和上边带的信号。当输入为单频率信号时，采用全载波SSB算法调制完全满足无失真包络平方条件。自解调信号和输入信号相比频率没有发生变化，不会产生失真现象，所以理论上采用全载波SSB算法对输入信号进行预处理，最终得到的自解调信号不存在失真现象，可以代替平方根法对音频信号进行预处理，产生无失真、高指向性的声参量阵信号。

2 仿真分析

研究的重点是用声参量阵来进行风速风向测量中的预处理算法的选择，基于时差法的声参量阵风速测试系统的最终性能直接与声参量阵信号顺、逆风传播的时间差Δt的精度有关，需对两个传声器阵列接收到的声参量阵信号通过广义互相关时延估计算法求得时间差Δt，采用不同的预处理算法得到的声参量阵信号不同，则通过时延估计算法得到的的精度也将不同，经全载波SSB法预处理后的声参量阵信号的时延估计精度理论上应该是最高的，但还需进项仿真验证。对采用三种预处理算法得到的声参量阵信号进行时延估计仿真分析，最终选出精度最高的预处理算法[7-8]。

在MATLAB中进行仿真，采用2 kHz音频信号，40 kHz的载波信号，采样频率为100 kHz，调制系数为m=0.7。采用不同的调制算法对音频信号进行预处理，得到的自解调信号加入高斯白噪声后，进行PHAT加权的广义互相关法时延估计。加噪的自解调信号作为时延估计算法所需的信号x1，对x1延时0.01 s作为信号x2，对x1和x2进行基于PHAT加权的广义互相关算法，画出互相关函数图并标出峰值，峰值对应的时刻即为延迟点数，然后通过时间和采样频率的关系公式求出延迟时间Δt，最后对仿真结果进行分析。序列长度为N=100 000，0.01 s对应的延迟点数为1 000个采样点。延迟时间的计算公式为

式（5）中，d为延迟点数，fs为采样频率。

1）采用全载波SSB法作为预处理算法，仿真结果如图3所示。

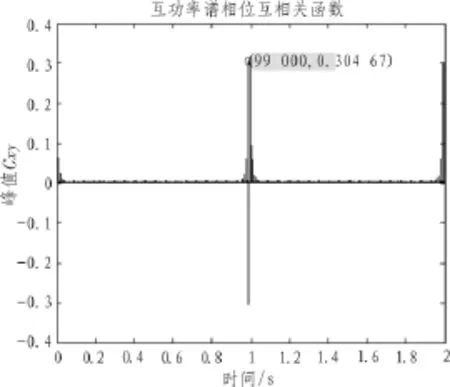
图3 基于PHAT加权的广义互相关函数波形（全载波SSB法）

由图3可看出，采用全载波SSB算法得到的互相关函数基本不受噪声干扰，函数波形很清晰，峰值十分突出，对应的时刻点数为n=99 000，则延迟点数为d=[99 000-100 000]= 1 000，进而由公式（3）求得延迟时间为Delay=1 000/100 000= 0.01 s，所求结果与预设延迟时间Δt=0.01 s相符合，说明预处理算法为全载波SSB法时，测得的时间差精度很高。

2）采用DSB法作为预处理算法时，仿真结果如图4所示。

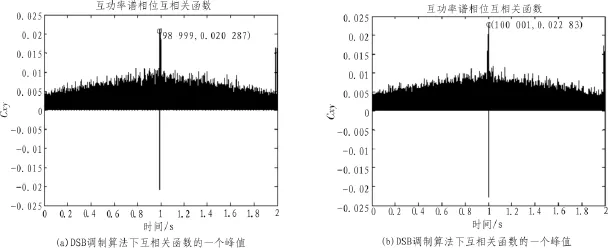
图4 基于PHAT加权的广义互相关函数波形图(DSB法)

由图4可以看出，采用DSB法做声参量阵系统的预处理算法时，每次仿真得到的峰值时刻在变化，仿真结果不太稳定，且受噪声影响较大，时延估计的精度不高，与预设延迟时间的误差较大。

3）采用平方根法作为预处理算法时，仿真结果如图5所示。

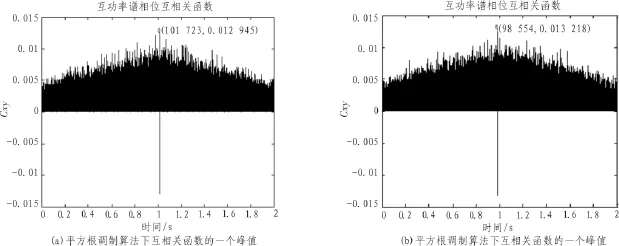
图5 基于PHAT加权的广义互相关函数波形图（平方根法）

由图5可以看出，采用平方根法作为声参量阵的预处理算法时，仿真结果受噪声影响很大，互相关函数的峰值几乎淹没在噪声中，很不突出，且峰值很不稳定，与预设值偏差很大，所以测得的时间差精度很低，误差比较大。

3 声参量测风速系统实验验证

根据建立的二维风速风向测量模型可知，整个测风系统中需要4个声参量阵发射接收阵，为了简化电路，提高系统的集成度，我们将发射阵和接收阵集合在一起，即将超声波换能器阵列和传声器阵列集合在同一面板上。参量阵风速测试系统的总体设计框图如图6所示。

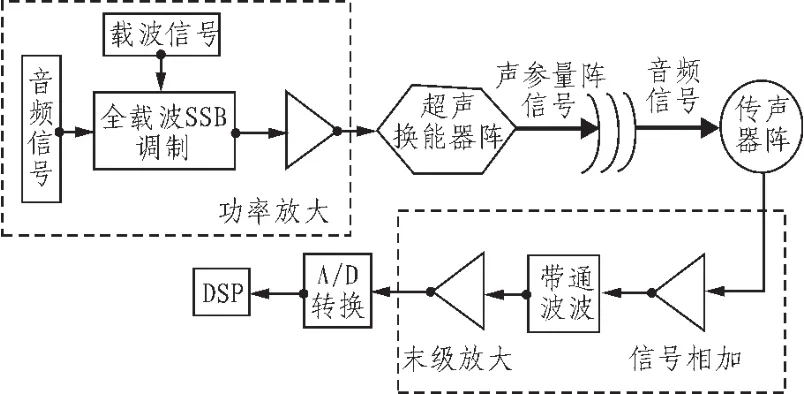
图6 参量阵风速测试系统总体设计框图

图6 中，超声换能器阵与传声器阵是分别用来发射超声波信号与接收音频声波信号的装置。在设计该阵列时需按照风速测试系统的性能要求选择适合的超声波换能器型号与传声器型号，参量阵测风速系统实物图如图7所示。

图7 声参量阵测风速系统的实物图

系统实验测试在声参量阵风速测试系统的设计中占有十分重要的地位，是对整个系统的性能和测量精度的实际验证。在无回声无风的空旷大厅中，将声参量阵风速测试系统和超声波风速风向仪进行对比试验，背景噪声约为10～35dB，并且音频信号的声压级高于背景噪声20dB以上，由信号发生器提供5 kHz的音频信号，BF533内部提供载波信号为40 kHz。由一台风力强劲的大型电扇提供实验所需的风场，将声参量阵风速测试系统和超声波风速风向仪放置在风场正中，分别记录它们测得的风速和风向值。电扇可以提供3个档位的风速。

超声波风速风向仪测量精度为0.2 m/s，分辨率为0.01 m/s，测风探头间距为20 cm，即超声波风速风向仪的测量空间范围大约为0.04 m2。声参量阵是两列具有一定频率差的已调超声波信号在空气中的传播过程中发生非线性效应而自解调出可听声的，所以，在其有效长度内，音频信号不断增强，在超出有效长度后则不断减弱。为了测得性能最好的可听声信号，测试距离需在接近声参量阵的有效长度处，该有效长度由I0=1/2a0决定。因为衰减系数a0载波的频率变化而变化，所以采用不同频率的载波时，最佳的测试距离也不同[9]。此处载波频率为40 kHz，则最佳测试距离为2 m，因此，设置声参量阵风速测试系统中的测风探头之间间距为2 m，则其风速测量范围大约为4 m2，是超声波风速风向仪测量范围的100倍，说明声参量阵风速测试系统可实现大空间范围内的风速测试。声参量阵风速测试系统的设计精度为0.1 m/s，分辨率为0.01 m/s。

实验数据如表1所示。

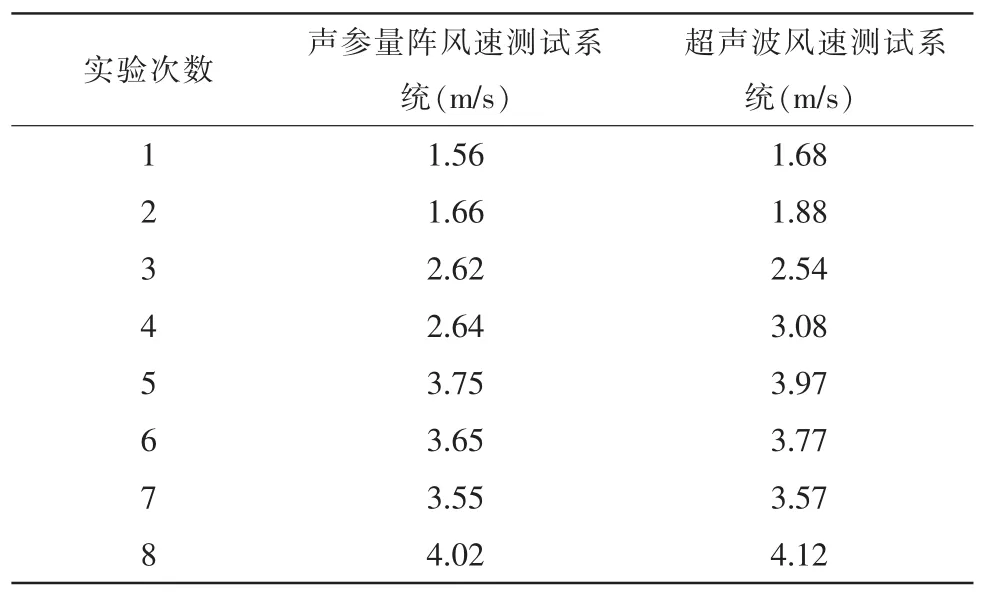
表1 实验数据对比表

从表1可以看出，在3个档位的风场中，声参量阵风速测试系统的分辨率为0.01 m/s，声参量阵风速测试系统测量风速时有0.1 m/s的跳变，超声波风速仪有0.2 m/s的跳变，由此可知声参量阵风速测试系统的测量精度为0.1 m/s，符合设计要求。声参量阵风速测试系统的测试结果比较稳定，且其测得的风速总是比超声波风速仪测得风速要低一些，符合理论分析情况，因为声参量阵测风系统测得的是2 m见方的空间内的平均风速，而超声波风速仪测得的是正对风扇的0.2 m见方的空间内的平均风速，所以前者的风速值理论上较小，实验结果也验证了这点。

4结 论

从理论和仿真两个层面阐述声参量阵测风速中信号预处理算法的选择，通过仿真结果分析可知，采用DSB法和平方根法作为声参量阵的预处理算法时，仿真结果易受到噪声的干扰，且峰值很不稳定，与预设值偏差较大，时延估计精度很低，不适合用于声参量阵风速测试系统；采用全载波SSB法作为预处理算法时，仿真结果很稳定，受噪声影响很小，与预设值一致，测得的时间差Δt很精确，时延估计精度很高。综合全载波SSB法的诸多优点及其对Δt的精确估计，采用全载波SSB法作为声参量阵风速测试系统的预处理算法，通过实验对比证明声参量阵测风速系统比超声波测风速系统测量空间更大，而且更加精确。

[1]刘圣军.声学参量阵技术研究[D].长沙:国防科学技术大学，2008.

[2]王亚丽.声学参量阵预处理算法研究及实现[D].重庆:重庆交通大学，2013.

[3]陈敏.声频定向系统理论与关键技术研究[D].成都:电子科技大学，2008.

[4]H.O.Berkay.Possible exploitation of non-linear acoustics in underwater transmitting applications[J].J.Sound Vib.，1965，2（4）:435-461.

[5]李学生.微型声频定向系统理论及关键技术研究[D].成都:电子科技大学，2012.

[6]宋朝晖，鲍可进.参量扬声器系统的探索与研究[J].电声技术，2005，（5）:28-30.

[7]罗中兴.基于 DSP的超声波风速风标测量系统研究[D].包头:内蒙古科技大学，2009.

[8]李广峰，刘防，高勇.时差法超声波流量计的研究[J].电测与仪表，2000，23（9）:13-16.

[9]张富东，周代英，陈敏.宽带水声参量阵指向性设计与实验验证[J].声学技术，2011，30（2），140-143.

Research on the application of acoustic parametric array to test wind speed

SONG Ye-qiang，CHEN Min，JIN Yin-rui，LI Xing-yong
（Institute of Astronautics and Aeronautics，University of Electronic Science and Technology of China，Chengdu 611731，China）

The signal pretreatment algorithm of acoustic parametric array wind speed test system is to generate two difference frequency carrier signals.The two signals via nonlinear interaction of self-demodulated to gain original signal in the air.Then make the two signals that received from microphone arrays through the PHAT weighted generalized cross correlation algorithm to estimate the time delay，and we calculate the wind speed by measure the time difference of the two signals.Preprocess the audio signal by the commonly used pretreatment algorithms，then the signals self-demodulation in the air to get parametric acoustic array signals and we analysis the results by MATLAB simulation.After the simulation analysis，full carrier SSB modulation algorithm got the highest precision of measured time，so full carrier SSB modulation algorithm is best suit for acoustic parametric array wind speed test system to preprocessing signal，we designed the acoustic parametric array wind speed test system，and the feasibility of the testing system is proved by experiments.

acousticparametricarray；pretreatmentalgorithm；generalizedcrosscorrelationmethod；timedifferenceaccuracy

TN911.7

A

1674－6236（2016）18-0050-04

2015-10-16 稿件编号：201510101

国家自然科学基金项目(61271286)

宋业强(1989—)，男，山东济宁人，硕士研究生。研究方向:非线性信号处理。