钨合金球形破片侵彻DFRP靶板的试验研究
2016-11-25毛亮王华姜春兰李明
毛亮, 王华, 姜春兰, 李明
(1.北京航空航天大学 宇航学院, 北京 100083; 2.北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081)
钨合金球形破片侵彻DFRP靶板的试验研究
毛亮1, 王华1, 姜春兰2, 李明2
(1.北京航空航天大学 宇航学院, 北京 100083; 2.北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081)
为研究钨合金球形破片对DFRP靶板的侵彻规律,利用弹道枪动加载设备,研究了两种质量的钨合金球形破片对不同厚度DFRP靶板的侵彻. 根据弹道试验结果,获得了弹道极限速度和靶板面密度的关系,并利用量纲分析法得到了弹道极限速度的经验关系式,其预测值与试验结果吻合较好;分析了DFRP靶板在钨合金球体高速撞击下的主要破坏模式及细观吸能机制,并且获得靶板面密度和钨合金球形破片的初始撞击速度对弹道吸能的影响规律.
钨合金球形破片;冲击侵彻;超高分子量聚乙烯纤维;弹道极限速度
超高分子量聚乙烯纤维(ultra-high molecular weight polyethylene fiber,UHMWPE)是一种由平均相对分子质量在100万以上的聚乙烯纺制而成的纤维,它是继碳纤维、硼纤维、芳纶之后的第4代纤维. 该纤维除了具有高比强度、比模量的特点以外,还具有良好的耐化学腐蚀、比能量吸收高、电磁波透射率高、摩擦因数低、优良的耐冲击和抗切割性能,以及不吸水、与生物相容性好等特点,并且是所有高性能纤维中相对密度最小的纤维. 因此,UHMWPE纤维复合材料是制作防弹装甲的极佳材料,在防弹领域具有广阔的应用前景[1-3].
钨合金球形破片具有最简单几何形状,而且密度大、保持速度和穿甲能力强,在预制破片杀伤战斗部中被广泛采用. 考虑到复合材料防护机理的复杂性,试验研究能直观地观测现象,揭示支配侵彻过程的主要影响因素和内在本质,因此,本文针对由荷兰DSM公司生成的UHMWPE纤维系列Dyneema UD75作为增强材料的层合板(dyneema fiber reinforced plastic,DFRP),进行了钨合金球形破片打靶试验,分析了钨合金球形破片侵彻DFRP靶板的作用过程及吸能机制,获得了不同质量钨合金破片垂直侵彻不同厚度DFRP靶板的弹道极限速度,并利用量纲分析法得到了弹道极限速度的经验关系式. 研究结果对杀伤战斗部和装甲防护结构的优化设计具有重要的应用和参考价值.
1 弹道试验
1.1 弹靶材料
本试验采用2 g和3 g(直径分别为6 mm和6.9 mm)两种质量的钨合金(93W-Ni-Fe)球体作为侵彻体,靶板用超高分量聚乙烯纤维增强树脂基复合材料为荷兰DSM公司生产的超高分子量聚乙烯纤维系列Dyneema UD75. 各材料具体性能参数如表1和表2所示. 表1中:ρp为钨合金球体密度;Yp为屈服强度;Tp为抗拉强度;δp为延伸率;ψp为断面收缩率;Ep为弹性模型;HRC为硬度;α为冲击韧性. 表2中:ρf为纤维材料密度;σbf为拉伸强度;Ef为拉伸模量;δf为延伸率.

表1 钨合金球体材料性能参数

表2 纤维材料性能参数
1.2 靶板制备
聚乙烯纤维增强树脂基复合材料层合板(DFRP)制备采用热压工艺,首先将Dyneema UD75预浸料按设计要求裁成一定尺寸,并正交铺层至所需厚度,放入模具中;然后将模具置于热压机上,升温速率为(2~3)℃/min,当温度稳定在120 ℃后,保温、加压;30 min后,自然冷却至室温、卸模. 根据所铺预浸料层数不同将会得到不同面密度的层合板.
1.3 试验装置
试验装置及其布置如图1所示,它包括弹丸专用发射器、防护装置、弹丸速度测试系统、靶架和残余体回收装置等. 弹丸专用发射器为12.7 mm的弹道枪,速度由发射药量控制. 为保证发射所必须的密封性和达到规定的速度,钨合金球被置于凹形的尼龙弹托中,待弹托飞离枪口后,在空气阻力作用下球与弹托分离,弹托自身也因受冲击而破碎,破碎后的弹托碎片会被防护板拦截,而球则通过防护板中心处小孔飞向靶板,球的撞靶速度及残余体速度分别由靶前和靶后的一组测速靶网和时间测试仪器来完成. 当撞击速度大于弹道极限速度时,球贯穿靶板后,其残余体和冲塞以及靶背面的崩落碎片将由残余体回收装置收容.
2 试验结果及分析
2.1 弹道极限速度分析
2.1.1 不同面密度靶板的弹道极限速度
弹道极限速度是衡量靶板在一定弹体侵彻下抗弹性能的重要指标,它指弹丸侵入靶板的最高速度和完全穿透靶板的最低速度的平均值,破片侵彻靶板的弹道极限速度可用v50或v100来表征. 大量实验证明,对于给定的弹靶系统,v50服从正态分布,当未贯穿数大于或小于贯穿数时,v50的计算公式分别为[4-5]
(1)
(2)
式中:vA为贯穿与未贯穿的混合区内所有速度的平均值;Np为混合区内未贯穿破片数;Nc为贯穿破片数;vpmax为未贯穿破片的最大速度;vpmin为贯穿破片的最小速度.
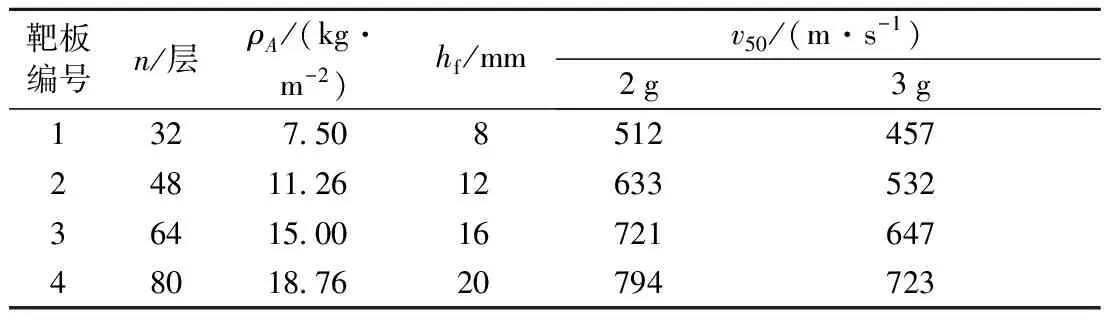
表3为试验得到的两种质量破片垂直侵彻不同厚度DFRP靶板的弹道极限速度值,表中:n为织物层数;ρA为面密度;hf为靶板厚度. 图2为其弹道极限速度值随DFRP靶板面密度的变化曲线.
表3 钨合金球形破片侵彻DFRP靶板的弹道极限速度
Tab.3 Ballistic limit velocity for tungsten alloy spherical fragment penetrating DFRP target plates
靶板编号n/层ρA/(kg·m-2)hf/mmv50/(m·s-1)2g3g1327508512457248112612633532364150016721647480187620794723
从图2中可以看出,随着靶板面密度的增加,钨合金球体侵彻DFRP靶板的弹道极限速度也增加. 对于相同面密度DFRP靶板,2 g钨合金球体的弹道极限速度要高于3 g钨合金球体.
2.1.2 弹道极限速度经验公式
由于复合材料的各向异性以及对材料在高应变率下的动态力学特性认识还不够清楚,关于破片侵彻复合材料靶板的许多问题至今利用解析法尚不能全部解决或者根本无法解决. 因此,需要在试验研究的基础上,建立起能满足实际应用的工程计算式.
钨合金球形破片垂直侵彻DFRP靶板的过程与许多参数有关,若忽略一切热效应,则弹道极限速度可表示为
(3)
式中:ρp,dp,εp,Cp,Yp,Ep,Gp,Hp分别为钨合金球形破片的密度、直径、特征应变、声速、屈服应力、弹性模量、剪切模量和硬化模量;ρf,hf,εf,Cf,Yf,Ef,Gf分别为DFRP层合板的密度、厚度、特征应变、声速、等效断裂强度、等效弹性模量和等效剪切模量.
根据量纲分析定理可得[6]
(4)
在球、靶材料不变条件下,钨合金球形破片侵彻DFRP靶板的弹道极限速度应遵从几何相似律,即球贯穿靶板的量纲一弹道极限速度仅是靶板厚度和球初始直径的函数. 于是,由式(4)可知,
(5)
式中K,α为待定常数.
对式(5)拟合,并利用弹道试验结果进行线性回归,从而可得到钨合金球形破片垂直侵彻DFRP靶板的弹道极限速度工程经验关系式为
(6)
式中v即为v50,由于式(6)是在量纲分析的基础上,根据试验结果拟合分析得到的,因此它适用于钨合金球形破片对DFRP靶板的侵彻贯穿,适用参数范围为v<1 200 m/s,1.16 表4 钨合金球形破片侵彻DFRP靶板的弹道极限速度的试验值与计算值的比较 Tab.4 Comparison between experimental and calculated values of ballistic limit velocity hf/mmdp/mmhf/dpv50/(m·s-1)试验值计算值相对误差/%8601335124990-2512602006336094-3716602677217022-2620603337947839-12869116457465917126917353256736616692306476529092069290723731911 从表4中的数据可以看出,对于钨合金球形破片-DFRP靶板系统,弹道极限速度计算值与试验值的相对误差平均值小于2.5%,最大单项误差为6.6%,满足工程应用要求. 2.2 破片侵彻过程分析 试验中发现,DFRP靶板在受到破片的高速撞击时,靶板的破坏过程呈现多阶段破坏模式,主要包含3个阶段,即纤维冲剪断裂(着弹面数层)-拉伸变形(隆起,分层)-纤维拉断贯穿,如图4所示. 图5为钨合金球体贯穿DFRP靶板后的靶板状态图. 当高速钨合金球体撞击DFRP靶板时,复合材料中的基体树脂在压应力作用下产生裂纹,聚乙烯纤维被软化,由于聚乙烯纤维具有高延伸率、高韧性的特点,它在破坏前发生较大程度的塑性变形,在靶板背面产生较大的隆起(鼓包),同时产生分层,钨合金球体继续侵彻靶板,当纤维变形达到最大应变时,纤维断裂. 同时,弹体冲击时产生大量热,使树脂软化、烧蚀. 此外,试验发现,钨合金球体侵彻DFRP靶板后没有发生明显的塑性变形,质量基本不发生变化,但其与靶板接触一面有明显烧蚀痕迹. 2.3 靶板吸能机制分析 2.3.1 DFRP靶板的吸能方式 DFRP靶板属于韧性复合材料靶板,由前述侵彻过程分析可知它的损伤破坏模式主要为分层及纤维断裂,因此,其吸能的细观机制主要包含分层、基体塑性变形、纤维脱黏、纤维拔出及断裂[7]. ① 分层. DFRP靶板在弹丸撞击加载作用下,局部将产生大的拉伸挠曲变形,同时产生分层破坏,分层将吸收一定的能量. ② 基体塑性变形. 当脆性纤维黏结在韧性基体中时,常常在裂纹前缘的纤维产生断裂,基体由于受力增大产生塑性变形,然后产生局部颈缩到最后全部断开. 这样表面能决定于使单位体积的基体产生塑性变形直到断裂所需之功. ③ 脱黏. 由于纤维的断裂应变比基体的断裂应变大,在基体材料开裂后,纤维继续被拉长. 同时,基体的开裂造成基体卸载、基体变形、变小. 这样,在纤维与基体之间,由于剪应力增加,而造成界面脱胶,这样一个过程将一直持续到纤维被拉断为止,一般认为脱胶所需的能量就是纤维拉长的附加应变能. ④ 纤维拔出. 纤维断裂时要使材料断开,必须把埋在基体中的纤维断口抽出来,抽出过程中必须首先破坏纤维与基体之间的界面,在这个过程中要吸收一定的能量. 此外,基体裂纹及应力重新分布也对能量吸收有贡献. 2.3.2 靶板面密度对弹道吸能的影响 由于钨合金球体的硬度远高于纤维增强复合材料的硬度,而且试验中也发现钨球贯穿DFRP靶板后基本不发生变形,因此可将钨球看成是一刚体,其侵彻与贯穿DFRP靶板的能量吸收可以由弹道试验结果,通过下式计算得到. (7) 式中:Ea为钨合金球形破片贯穿靶板过程中靶板吸收的能量;mp为钨合金球形破片的质量;vi为钨合金球形破片穿靶前的初始速度;vr为钨合金球形破片穿透靶板后的剩余速度. 在弹道极限速度时,vr=0,于是 (8) 若设γBPI为弹道性能指数,即单位面密度靶板吸收的能量;γEI为能量吸收指数,即单位厚度靶板吸收的能量,则γBPI=Ea/ρAD,γEI=Ea/hf. 表5给出了不同面密度ρA的DFRP靶板在弹道极限速度时靶板吸收的能量Ea、弹道性能指数γBPⅠ以及能量吸收指数γEI. 图6给出了靶板吸收的能量随靶板面密度的变化曲线. 表5 DFRP靶板在弹道极限速度时的弹道吸能 Tab.5 Ballistic absorbing energy of DFRP target plates on ballistic limit velocity hf/mmρA/(kg·m-2)Ea/JγBPI/(J·m2·kg-1)γEI/(J·mm-1)2g3g2g3g2g3g8750262313349417328391121126401425356377334354161500520628346418325393201876630784335418315392 从图6中可以看出,在弹道极限速度附近,DFRP靶板的能量吸收随着靶板面密度的增加而增加. 此外,3 g的钨合金球体贯穿DFRP靶板其能量吸收增加率明显大于2 g的钨合金球形破片,即随着靶板面密度的增加,靶板对大质量破片贯穿的吸能性增强. 对于相同面密度的靶板,3 g钨合金球体侵彻靶板所吸收的能量高于2 g钨合金球体,即大质量、大直径破片比小质量、小直径破片贯穿同样厚度的靶板需要较多的能量. 这是由于对于厚的DFRP靶板,直径大的钨合金球体所受的弹道阻力较大,更易于DFRP层合板产生拉伸破坏,从而有利于纤维应变率效应的充分发挥,导致靶板吸能增加. 从表5中可知,在弹道极限速度时,3 g钨合金球体侵彻靶板的弹道性能指数和能量吸收指数都明显高于2 g质量的钨合金球体,但与靶板面密度关系不大. 2.3.3 破片速度对弹道吸能的影响 钨合金球形破片侵彻DFRP靶板的过程是一个高速动态的过程,应变率效应不可忽视. 为了考察破片速度对DFRP靶板弹道吸能的影响,选取了厚度为8 mm和20 mm的DFRP靶板,利用2 g钨合金球体对其进行了不同初始速度下的弹道冲击试验. 表6给出了在破片不同入靶及出靶速度下两种不同厚度DFRP靶板的弹道吸能情况. 图7为两种不同厚度DFRP靶板的能量吸收随入靶速度的变化情况. 表6 DFRP靶板在破片不同撞击速度下的弹道吸能 Tab.6 Ballistic absorbing energy of DFRP target plates on different impact velocity h/mm820vi/(m·s-1)vr/(m·s-1)Ea/JγBPI/(J·m2·kg-1)γEI/(J·mm-1)6460376027636834580106250251334314854068402613483269670824025634132012030109402503333148347293461132530699774344806430403127548677874466437134159414913486457 从图7中可以看出,在钨合金球体贯穿DFRP靶板后,8 mm厚的DFRP靶板吸收的能量随入靶速度vi的增加变化不大,甚至略有降低,应变率效应不明显;而20 mm厚的DFRP靶板吸收的能量却随入靶速度vi增加而呈上升趋势,表现出明显的应变率效应. 试验结果表明,在薄板情况下Ea-vi关系与纤维复合材料的本身应变率效应不吻合. 这种不吻合的原因可以从弹击时靶板的破坏机理上得到解释. DFRP靶板由于纤维熔点低,在破片以较高速度撞击靶板时,摩擦生热瞬间无法耗散,导致DFRP靶板呈明显的多阶段破坏模式,即着弹面为冲塞破坏(垂直靶板面的剪切破坏),背面为拉伸破坏. 对于薄靶板,当速度超过最小穿透速度,达到一定值后,纤维来不及产生应变而破坏,造成因冲塞剪切破坏的纤维厚度增加,拉伸破坏的纤维减小,能量吸收值有可能下降,因而应变率效应不明显. 对于厚靶板而言情况则不同,在相同撞击速度条件下,靶板着弹面因冲塞破坏消耗了一定的破片动能,使钨合金球体速度降低,而背面仍有较多的纤维层产生拉伸破坏,因此随着弹速的提高,厚靶板背面产生拉伸破坏的材料产生的拉伸应变速率提高了,使得DFRP靶板的断裂强度、断裂应变均提高,钨合金球体穿透靶板的阻力增加,从而使靶板的弹道吸能Ea值也随之升高. ① 随着靶板面密度的增加,钨合金球形破片侵彻DFRP靶板的弹道极限速度也随之增加;且对于相同面密度的靶板,2 g的钨合金球形破片的弹道极限速度要高于3 g的钨合金球形破片. ② 利用量纲分析法得到了钨合金球形破片侵彻DFRP靶板的弹道极限速度计算公式,且利用该公式计算得到的预测值与试验值吻合较好,满足工程应用要求. ③ 分层和纤维断裂是DFRP靶板在高速钨合金球形破片侵彻下的主要损伤破坏模式,其吸能的细观机制主要包含分层、基体塑性变形、纤维脱黏、纤维拔出及断裂. ④ 在弹道极限速度时,DFRP靶板的能量吸收随着靶板面密度的增加而增加,3 g钨合金球体侵彻靶板的弹道性能指数和能量吸收指数都明显高于2 g质量的钨合金球体,但与靶板面密度关系不大. 此外,3 g的钨合金球体贯穿DFRP靶板其吸收的能量和能量吸收增加率要大于2 g的钨合金球形破片. ⑤ 钨合金球体贯穿DFRP靶板后,8 mm厚的DFRP靶板吸收的能量随入靶速度vi的增加变化不大,甚至略有降低,应变率效应不明显;而20 mm厚的DFRP靶板吸收的能量却随入靶速度vi增加而呈上升趋势,表现出明显的应变率效应. [1] 郑震,施楣梧,周国泰.超高分子量聚乙烯纤维增强复合材料及其防弹性能的研究进展[J].合成纤维,2002,31(4):20-26. Zheng Zheng, Shi Meiwu, Zhou Guotai. Progress in ultrahigh molecular weight polyethylene fiber reinforced composites and its bulletproof property[J]. Synthetic Fiber in China, 2002,31(4):20-26. (in Chinese) [2] 王晓强,朱锡,梅志远.高速钢质破片侵彻高强聚乙烯纤维增强塑料层合板试验研究[J].兵工学报,2009,30(12):1574-1578. Wang Xiaoqiang, Zhu Xi, Mei Zhiyuan. An experimental research on high velocity steel fragments perforation UHMEWPE FRP laminates[J]. Acta Armamentarii, 2009,30(12):1574-1578. (in Chinese) [3] 陈长海,朱锡,王俊森,等.高速钝头弹侵彻中厚高强聚乙烯纤维增强塑料层合板的机制[J].复合材料学报,2013,30(5):226-235. Chen Changhai, Zhu Xi, Wang Junsen, et al. Mechanism of high-velocity blunt-nosed projectiles penetration moderately thick UHMWPE fiber reinforced plastic laminate[J]. Acta Materiae Compositae Sinca, 2013,30(5):226-235. (in Chinese) [4] 王海福,刘志雄,冯顺山.钢球侵彻钛合金靶板弹道极限速度[J].北京理工大学学报,2003,23(2):162-164. Wang Haifu, Liu Zhixiong, Feng Shunshan. Ballistics limit velocity for spherical steel fragments penetrating titanium-alloy target plates[J]. Transactions of Beijing Institute of Technology, 2003,23(2):162-164. (in Chinese) [5] 美国陆军器材部.终点效应设计[M].李景云,习春,于骐,译.北京:国防工业出版社,1988:218-225. American Army Equipment Department. Design of terminal effect[M]. Li Jingyun, Xi Chun, Yu Qi,transl. Beijing: National Defense Industry Press, 1988:218-225. (in Chinese) [6] 欧阳楚萍,徐学华,高森烈.相似与弹药模化[M].北京:兵器工业出版社,1995:38-62. Ouyan Chuping, Xu Xuehua, Gao Senlie. Similar and ammunition modeling[M]. Beijng: Ordnance Industry Press, 1995: 38-62. (in Chinese) [7] 张双寅,刘剂庆,于晓霞,等.复合材料结构的力学性能[M].北京:北京理工大学,1992. Zhang Shuangyin, Liu Jiqing, Yu Xiaoxia, et al. Mechanical properties of composite material structure[M]. Beijing: Beijing Institute of Technology, 1992. (in Chinese) (责任编辑:刘雨) Experimental Research on Tungsten Alloy Spherical Fragment Penetrating DFRP Target Plates MAO Liang1, WANG Hua1, JIANG Chun-lan2, LI Ming2 (1.School of Astronautics, Beihang University, Beijing 100083, China; 2.State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology,Beijing 100081,China) Making use of ballistic gun equipment, the effect was studied that dyneema fiber reinforced plastic (DFRP) target plates with different thickness was impacted by two different tungsten alloy spherical fragments. Firstly, according to the ballistic experimental results, the relationship between ballistic limit velocity and target plates area density was obtained. Besides, the empirical formula of ballistic limit velocity was built according to the dimensional analysis method, and the predictive value with the empirical formula was consistent with the experimental results. Secondly, the main failure mode and energy absorption mechanism were analyzed for DFRP target plates impacted by tungsten alloy spherical fragments. Also, the influence of target area density and initial velocity of the tungsten alloy spherical fragment on ballistic absorbing energy was obtained. The research results are valuable for designing fragment warhead and light armor protective structure. tungsten alloy spherical fragment; impact and penetration; ultra-high molecular weight polyethylene fiber; ballistic limit velocity 2014-06-26 国家部委基础科研计划资助项目(A2220110003) 毛亮(1985—),男,博士后,E-mail:maoliang6419@163.com. O 385 A 1001-0645(2016)04-0348-06 10.15918/j.tbit1001-0645.2016.04.003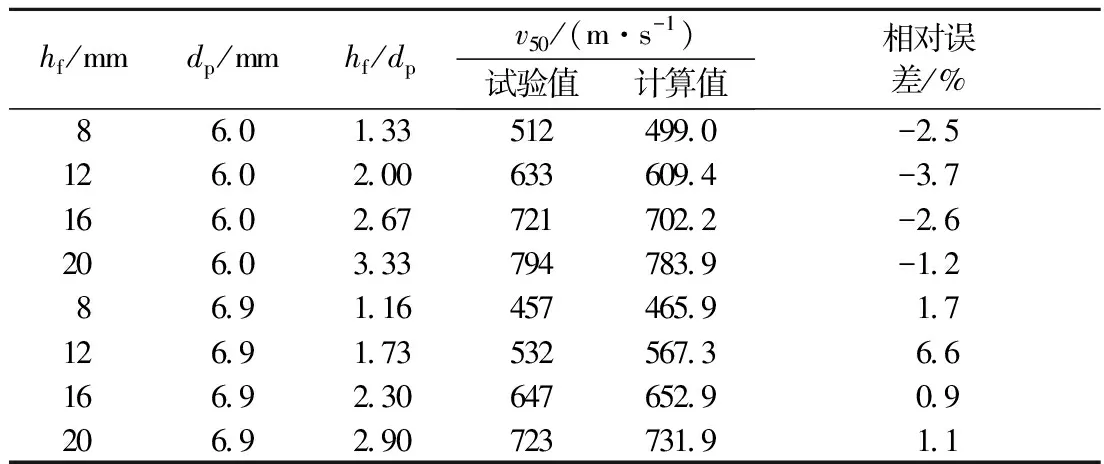
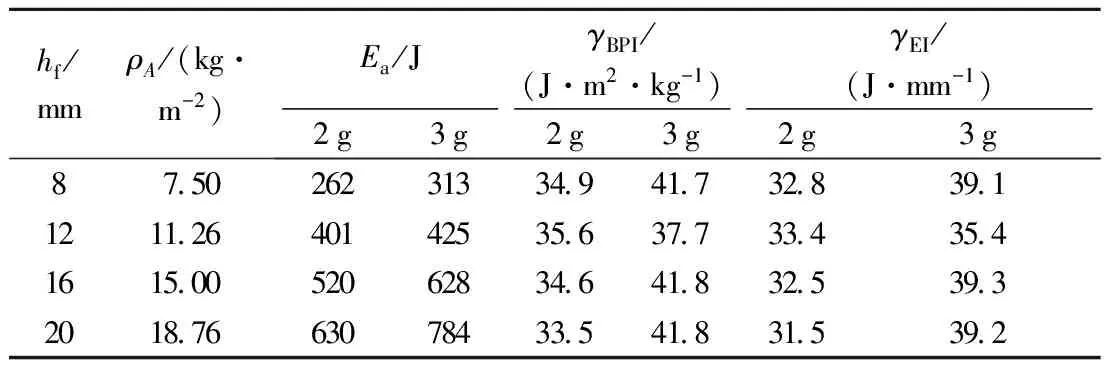
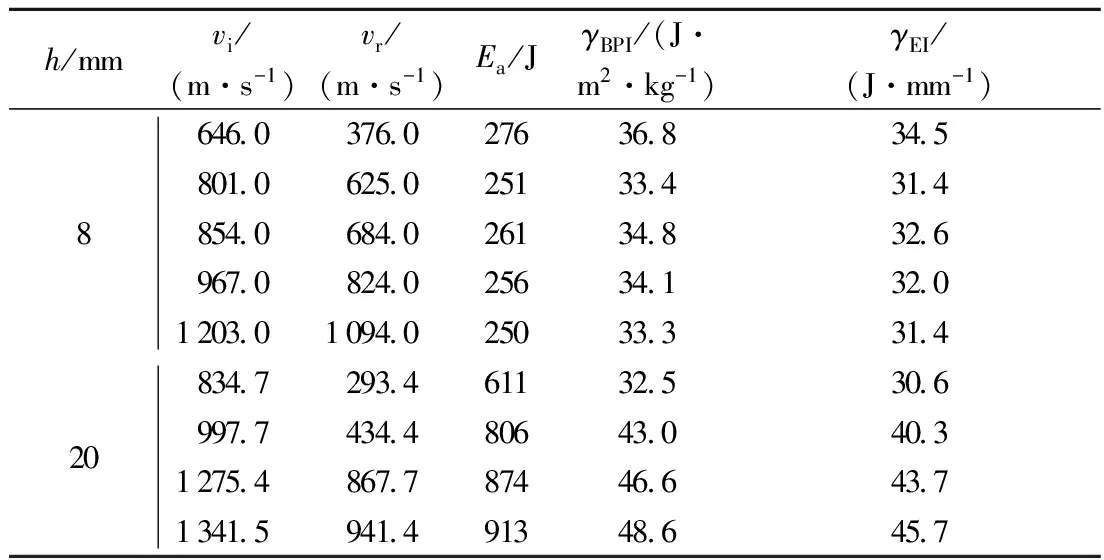
3 结 论
