SLAM中融合形状上下文和随机步进的图匹配数据关联算法

华承昊， 窦丽华， 方浩， 付浩

(1.北京理工大学 自动化学院，北京 100081；2.国防科技大学 机电工程与自动化学院，湖南，长沙 410073)



SLAM中融合形状上下文和随机步进的图匹配数据关联算法

华承昊1， 窦丽华1， 方浩1， 付浩2

(1.北京理工大学 自动化学院，北京 100081；2.国防科技大学 机电工程与自动化学院，湖南，长沙 410073)

提出了一种在非确定环境下求解SLAM数据关联问题的图匹配算法. 算法建立了SLAM中数据关联的图论模型，对图模型节点提取了不依赖位置信息的形状上下文特征(shape context，SC)，最后通过二次加权随机步进算法(reweighted random walks，RRW)得到图匹配问题的优化解. RRW&SC图匹配算法充分利用了路标间的拓扑结构关系以及路标间的形状结构，极大地扩展了数据关联时所依据的几何信息量. 仿真实验结果表明，与传统算法相比，该算法能有效处理SLAM中噪声干扰增加、机器人迷失、路标被动态遮挡等不确定程度高、歧义性大环境中的数据关联.

数据关联；图匹配；同步定位与建图

SLAM是移动机器人在未知环境中以起始出发点为原点，通过自身携带传感器测量的环境特征数据，在移动中不断自我定位同时逐步绘制出其经过环境地图的过程[1-2]. 数据关联则是机器人SLAM中保障地图绘制精准与鲁棒性的关键环节[3]. 经过多年的探索，依据机器人所携带传感器和所创建地图模型的不同，研究人员提出了众多的数据关联算法. 现有的SLAM算法依据地图表示类型可分为由传感器原始数据生成度量地图(metric map)或者栅格地图(grid map)的SLAM算法，和对传感器原始数据进行特征路标提取后的特征地图(feature map)的SLAM算法. 其中，特征地图匹配的数据关联算法可以分为两类.

第一类算法是以观测数据与已绘地图路标间的马氏距离(Mahalanobis distance)规则来求解数据关联问题. 典型方法包括独立相容的最近邻匹配(individual compatibility nearest neighbor， ICNN)[3]、 联合相容的分枝限界匹配(joint compatibility branch and bound， JCBB)[3]、多假设跟踪的数据关联算法(multi-hypothesis tracker， MHT)[4]及各自的衍生算法等. 这类算法计算复杂度低、有助于SLAM增强实时性，但也有因马氏距离含有的信息量低而难以解决错误数据关联的缺陷. 当SLAM进行闭环检测时，需采用较大的马氏距离阈值，因此易产生多重数据关联；而在环境特征相对密集时，需采用较小的马氏距离阈值从而易导致错误的数据关联. 郭帅等[5]指出：“多重数据关联问题和错误数据关联问题对马氏距离阈值提出了相互矛盾的要求，寻找一个合适的马氏距离阈值是一个复杂或者难以完成的任务. ”即使研究者们提出诸多可保留多种数据关联可能性的多假设算法[4，6-7]，也始终无法摆脱马氏距离规则几何信息含量少的根本缺陷，无法有效地解决多重数据关联和错误数据关联问题.

第二类算法则希望利用观测数据中蕴含的拓扑结构等更多的几何信息来求解数据关联问题. 如Bailey等[8]以环境特征的位置、特征间连线的距离、连线间的夹角以及特征到连线的垂直距离等拓扑关系，构成特征图. 通过在观测数据与已绘地图间寻找最大公共子图来获得数据关联. 该方法对错误关联有很强的抗干扰能力，但是未能很好地解决搜索最大公共子图这个不易求解的NPC(non-deterministic polynomial-complete)问题. Gamallo等[9]将匈牙利算法(Hungarian algorithm， HA)引入SLAM中的数据关联求解. 该算法是求解分配问题最常见的优化算法，其核心是以Hall定理为依据寻找增广路径求解二分图的最大匹配[9-10]. 文献[5]中则对环境特征采用轮廓角度、轮廓面积两个参数加以描述，提出了轮廓匹配规则的数据关联算法. 这类数据关联算法为避免错误关联、获得更鲁棒的关联结果提供了更广阔的思路，但对观测数据蕴含几何信息的运用仍不够充分，因而在机器人迷失等情形时难以有良好的表现.

在现实环境中，机器人常常面对各种非确定、突发状况的挑战. 比如，机器人传感器偶发故障或者因环境扰动影响带来的运动噪声或者观测噪声的增大，机器人被碰撞或者被人为突然转移带来的位姿迷失，机器人所在环境路标被其他动态移动物体遮挡等等. 面对环境中这些非确定状况时，仅依赖待匹配数据间的距离信息的数据关联算法就难以有良好的表现. 此时，待匹配数据中蕴含的拓扑结构信息就能为准确数据关联提供有效支持. 在应对这些非确定环境状况时，为了能更充分有效地运用观测数据中蕴含的几何拓扑结构信息，获得准确、鲁棒的数据关联结果，本文提出了一种结合二次加权随机步进[11]和形状上下文[12]的图匹配数据关联算法(RRW&SC). 该算法既使用了多个路标的形状结构和路标间构成的拓扑结构信息，也利用了传统数据关联算法中机器人观测数据与已绘地图路标位置信息提供的马氏距离差，极大地扩展了数据关联时所依据的几何信息量. 且RRW&SC算法可以独立于数据关联匹配的历史纪录.

为验证提出算法的有效性，设定了非确定环境里常见的3种复杂状况：运动与观测噪声增大、机器人迷失以及路标被动态遮挡. 并通过仿真实验将RRW&SC算法与马氏距离最近邻算法、匈牙利分配算法等两类经典数据关联算法进行了对比. 仿真结果表明，在不确定程度高、歧义性大的复杂非确定环境中，RRW&SC算法能更有效地求解SLAM的数据关联问题.

1 问题描述与建模

1.1 SLAM中的数据关联

数据关联是研究机器人SLAM、目标跟踪等诸多自主智能化问题中的重要环节. 以SLAM研究领域中创建的平面地图为例，在某一时刻t，移动机器人R获得了其观测范围内m个环境特征的观测数据集. 观测数据集中的每一个特征值zi，与来源于同一环境的历史观测数据集(从初始时刻到t-1时刻)所绘制环境地图的各个特征值lj之间，都可以按照某一个确定的映射关系f确定地得到一定的对应关系，表示为f:zi→lj. 在来源于同一环境特征值之间对应关系的映射对中，甄选出最佳对应匹配关系的过程，就是数据关联[13].

(1)

(2)

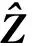
(3)

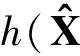
若Zt中的第i个特征与地图中的第j个特征对应实际环境中的同一个特征，那么它们间的马氏距离应服从自由度为m的χ2分布[5]. 以某一置信度(如95%)的χ2分布数值为阈值，即可作为SLAM中判断数据关联的依据. 通常，机器人在某时刻观测获得的环境特征有多个，多个特征间除了各自的位置信息外还有相互间的夹角、距离等拓扑结构信息. 若能将这些几何关系都用于求解数据关联，可有助于解决SLAM中多重数据关联和错误数据关联问题，增强SLAM的鲁棒性.

1.2 SLAM中数据关联的图论模型

图论里通常用一个4元组来描述一幅含有n个节点和m条边图的拓扑关系[15]，

式中：P为节点的集合；Q为节点间连通边的集合；G，H∈{0，1}n×m为拓扑关联矩阵，gic=hic=1表示第c条边是从i节点起始到j节点结束的.

图论模型中，机器人在其观测范围内对环境特征(如路标)的当前观测数据Z，与来源于同一环境中历史观测数据形成的已绘地图L，是同一环境中的两个节点集；而节点间的连线形成边集. 假定，已绘环境地图包含n个环境特征，其图模型Gtp1={P1，Q1，G1，H1}；当前观测信息含有m个观测特征值，其图模型Gtp2={P2，Q2，G2，H2}.

Gtp1和Gtp2间各节点相似度的仿射矩阵为

Gtp1和Gtp2间各边相似度的仿射矩阵为

假设n≥m，并按如下规则合并成Gtp1和Gtp2间拓扑相似度的仿射矩阵[10]为

(4)

式中:i1，i2∈(1，2，…，n);j1，j2∈(1，2，…，m);i1j1为K的行序号，i2j2为K的列序号.

给定Gtp1，Gtp2和K，SLAM中的数据关联就转化为求取Gtp1和Gtp2节点间的最佳匹配矩阵X*，使下面这个带约束的目标函数取极大值，

(5)

式(5)可视为求解SLAM中数据关联问题的一般化表示. 当Kp为马氏距离且Kq=0时，就可以采用基于马氏距离规则的算法求解. 若放宽式(5)的约束条件，则可以运用多假设数据关联算法求解. 若仅考虑只含有一阶拓扑信息节点位置的Kp，在机器人定位误差增大或者迷失等歧义性大的情形下，无法保证正确的数据关联. 因此需要引入边相似度仿射矩阵Kq. 引入Kq后，总相似度仿射矩阵K含有的拓扑信息就从一阶扩展为高阶. 这样则使得求解式(5)成为一个NPC问题. 因此需寻求一种有效鲁棒的求解方法.

2 RRW&SC图匹配数据关联算法

在建立SLAM数据关联图论模型的基础上，本文提出二次加权随机步进结合形状上下文的优化算法RRW&SC来求解式(5).

映射f:Gtp1Gtp2为Gtp1各节点进行了某种刚性的变动. 将Gtp1中某个节点与Gtp1和Gtp2各个节点所有可能的匹配(状态)视作是一个随机步进(random walks)运动.Gtp1和Gtp2间相似度仿射矩阵K中的非零元素描述了Gtp1和Gtp2节点与边之间的相似性. 如果对K按行归一化，这样就可得到一个随机步进矩阵. 一个随机步进矩阵对应的是一个遍历的Markov链，任意两个状态间按一定的转移概率随机步进.

求解式(5)就是找出随机步进中最符合仿射矩阵K的变动. 为此，本文引入了二次加权的随机步进(RRW)算法[11]. 该算法在文献[11]中被应用于对图形匹配问题的求解，本文将该算法进行改进，运用到了SLAM数据关联问题的求解中. 具体解法如下.

算法首先构造了可保持仿射关系K的随机步进状态转移矩阵

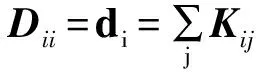
令

dmax=maxidi，

用dmax对仿射矩阵K行归一化，为

归一化的同时，为了表征dmax-di的差，并保证状态转移矩阵的收敛性，设计了一个带吸收态xabs的Markov链. 经过仿射关系保持的加权后，随机步进的状态转移矩阵P满足

(6)

式中x(n)为状态x的第n步状态转移.

式(6)是一个准稳态分布，可以证明其结果必然收敛[11]. 式(5)中除了仿射关系矩阵外，还需要满足匹配最多存在单一对应约束条件. 因此，通过再次加权的方式，将约束条件

加入到随机步进中，即在式(6)中添加了符合约束的状态匹配再加权跳转向量r. 构建r分两步：

① 令rT=exp(βx/maxx)，这可以使得概率值大的x更大，概率值小的x更小，式中β为膨胀系数；

② 对rT的行和列交替归一化，不断迭代，直至rT收敛. 可以证明rT必然收敛到满足式(5)约束条件的方阵[11].

在式(6)以及再加权跳转向量r的基础上，进一步假设，状态x以α的概率随机状态转移，以1-α的概率随机跳转. 就得到二次加权随机步进的状态转移公式为

(7)

迭代求解式(7)直至收敛，将得到的连续解离散化，即式(5)的优化解X*.

在现实环境中，特征的位置存在被遮挡、因机器人迷失或运动误差过大而被误测量等多种非确定情形. 此时，仅用位置信息描述环境特征，已难以保障SLAM过程中数据关联的准确性. 为了使环境特征属性的表示更具有鲁棒性，本文使用形状上下文算法[12]描述图节点的属性. 该算法使用特征点邻近区域所有节点与其相对位置信息来衡量该特征点的属性. 以Gtp1中某个节点pi为例，将pi为原点并覆盖其他所有节点的对数极坐标空间，按30°划分为12等分，再按对数距离lgρ将空间的半径划分为5部分，这样得到60个分块区域. 采用对数极坐标描述，可使与距离近的节点在描述属性上有更大的影响权重. 对整个空间记录除pi外的其余节点在这60个部分的分布数目的直方图hi，作为pi的属性描述

(8)

那么，来自于Gtp1的节点pi与来自于Gtp2的节点pj的相似度就可用下式描述

(9)

用形状上下文算法描述Gtp1和Gtp2间各节点相似度的仿射矩阵Kp，是通过提取节点集的形状模式来获得相似度匹配. 形状模式本身与图节点的位置无关，而且对于旋转等刚性变换具有固有的不变性. 同时，形状上下文算法所提取的形状模式，对于部分遮挡、少量噪声点等引起的图几何形变也有很好鲁棒性. 这些优点，都有助于非确定环境下的数据关联问题求解.

RRW&SC算法的主要流程如图1所示.

3 仿真实验与分析

在开源SLAM仿真程序的基础上[16]，创建了一个非确定环境下机器人SLAM数据关联的仿真平台. 在一个200 m×200 m的仿真空间内，放置了若干由星号表示的路标，机器人按预定轨迹匀速移动，如图2所示.

为了更好地检验、对比各个数据关联算法，设定机器人能观测到整个仿真环境. 机器人的运动噪声σv=0.3 m/s，σo=3°；测量噪声σρ=0.1 m，σα=3°.

实验分别模拟了以下3种情形.

① 模拟噪声干扰，逐倍增加机器人的运动误差和观测误差，来检验算法对大噪声的鲁棒性；

② 设置机器人的迷失情景，逐倍增加其距离的迷失并伴有朝向角度的随机迷失，测试算法能否实现迷失后恢复正确的数据关联；

③ 模拟机器人观测受到动态运动物体的遮挡，随着被遮挡路标数量的增加，测试算法在动态环境里的数据关联效果.

在仿真中，将本文的RRW&SC图匹配算法与马氏距离规则算法、匈牙利分配算法进行了对比. 实验结果和分析如下.

3.1 噪声干扰增加实验

当噪声从1倍逐倍增加至10倍，对每一种情形都重复进行了20次蒙特卡洛实验，结果见图3. 各个算法关联平均准确率的统计结果显示，本文提出的RRW&SC图匹配算法和匈牙利算法对大噪声干扰有很强的鲁棒性. RRW&SC算法能够始终保持完全正确的数据关联结果，匈牙利算法则有个别时刻出现少量的错误关联. 而基于马氏距离规则的算法只有在常规较小噪声时能得到完全正确的数据关联结果，随着噪声干扰的增加，其数据关联错误率呈增大趋势.

3.2 机器人迷失场景实验

在迷失情形下，设定机器人的初始迷失距离为4.6 m，并伴有朝向角的随机迷失. 逐倍增加机器人迷失的距离，最高至10倍即46 m. 对每一种情形都重复进行了20次蒙特卡洛实验，结果见图4. 各算法关联准确率的统计结果显示，RRW&SC图匹配算法在机器人迷失后，可以立即恢复正确的数据关联. 匈牙利算法的正确率出现大幅波动且很少能获得100%的准确关联，其在各次实验中的平均正确率都少于40%. 基于马氏距离规则的算法一旦遇到机器人迷失的情景，就基本无法有效地进行数据关联了. 这是由于该类算法仅依赖于位置信息所致，一旦机器人的定位出错，其观测的路标位置也随之出错. RRW&SC算法则能够在机器人定位出错的情形下，依靠观测数据中保留的拓扑图结构信息获得正确的数据关联.

3.3 动态遮挡情形实验

考察机器人观测受到动态运动物体的遮挡，且被遮挡路标数量不断增加的情形. 被遮挡路标数从2个逐步倍增到20个，对每一种情形都重复进行了20次蒙特卡洛实验，结果如图5所示.

各个算法关联准确率的统计结果显示，当数量不多的路标被遮挡时，RRW&SC图匹配算法能有效地应对，获得完全正确的数据关联结果. 可是当路标被遮挡多于一定数量时，RRW&SC算法也开始出现少量错误关联. 而匈牙利算法在路标有被动态遮挡时就无法获得完全正确的数据关联，算法的关联正确率随着路标遮挡数量的增加而明显下降，从95.68%降至为67.27%. 在动态遮挡的环境里，匈牙利算法的正确率很难满足SLAM的要求. 而基于马氏距离规则的算法，在动态遮挡环境下的有效性则表现出一定的差异. 在20次实验中，有14次的数据关联结果完全正确. 但出现错误关联时，该算法的正确率将大幅降低，且这些关联错误难以恢复，将导致SLAM完全发散. 在动态遮挡的情形下，将多假设算法结合马氏距离规则，应能使关联正确率提高并使得关联错误恢复得到较大改善.

仿真实验结果验证了RRW&SC图匹配数据关联算法大大超过马氏距离规则算法、匈牙利分配算法这两个SLAM经典数据关联算法的关联正确率. RRW&SC算法在模拟的3种不确定程度高、歧义性大的复杂情形下，仅在动态遮挡时图匹配算法出现了数据关联错误，且是在路标被遮挡数超过10个后. 相应于RRW&SC算法的优良性能，算法的计算复杂度也有增加.

4 结 论

提出了二次加权随机步进结合形状上下文的图匹配数据关联算法(RRW&SC). 算法的突出特点是：能更充分地利用机器人在SLAM过程中观测获得环境路标的位置信息和拓扑结构信息；克服了常用数据关联算法利用的信息含量低，在不确定程度高、歧义性大的非确定环境中难以保障关联结果正确性等缺陷. 实验结果显示，在面对噪声干扰增加、机器人迷失、路标被动态遮挡等环境中常见的非确定状况时，RRW&SC算法能有效地实现正确关联.

在动态遮挡环境中，当被遮挡路标数目较多时，RRW&SC算法出现了少量的错误关联. 若能更好地处理动态遮挡带来的拓扑信息变化，则能减少数据关联的错误. 相比于传统数据关联算法，本文算法提升了在非确定性环境中数据关联的性能，但因求解二次加权随机步进的复杂度较高，导致总的计算复杂度也有增加，后续研究可在这两方面有所改进.

[1] Durrant-Whyte H， Bailey T. Simultaneous localization and mapping: part I[J]. IEEE Robotics and Automation Magazine，2006， 13(2): 99-110.

[2]Wang Lu， Cai Zixing. Progress of CML for mobile robots in unknown environments[J]. Robot， 2004，26(4):380-384.

[3] Neira J， Tardos J. Data association in stochastic mapping using the joint compatibility test[J]. IEEE Transactions on Robotics and Automation， 2001，17(6):890-897.

[4] Jensfelt P， Kristensen S. Active global localization for a mobile robot using multiple hypothesis tracking[J]. IEEE Transactions on Robotics and Automation， 2001，17(5):748-760.

[5] Guo Shuai， Ma Shugen， Li Bin， et al. A data association approach based on multi-rules in VorSLAM[J]. Acta Automatica Sinica， 2013(6):522-527.

[6] Chen Baifan， Cai Zixing， Zou Zhirong. A multiple hypotheses data association method in mobile robot SLAM[J]. Journal of Central South University： Science and Technology， 2012，43(2):522-527.

[7] Kwok N， Dissanayake G. An efficient multiple hypothesis filter for bearing-only SLAM[C]∥Proceedings of International Conference on Intelligent Robots and Systems(IROS 2004). [S.l.]:IEEE， 2004：736-741.

[8] Bailey T， Nebot E M， Rosenblatt J K， et al. Data association for mobile robot navigation: a graph theoretic approach[C]∥Proceedings of the IEEE International Conference on Robotics and Automation. San Francisco， USA： IEEE， 2000：2512-2517.

[9] Gamallo C， Mucientes M， Regueiro C. Visual fastSLAM through omnivision[C]∥Proceedings of the Towards Autonomous Robotic Systems (TAROS 09). Derry， UK:[s.n.]， 2009:12-14.

[10] Vivet D， Checchin P， Chapuis R. Line-based SLAM with slow rotating range sensors: results and evaluations[C]∥Proceedings of 2010 11th International Conference on Control Automation Robotics & Vision (ICARCV). [S.l.]: IEEE，2010:423-430.

[11] Cho M， Lee J， Lee K M. Reweighted random walks for graph matching[C]∥Proceedings of Computer Vision-ECCV 2010. Berlin， Heidelberg: Springer， 2010:492-505.

[12] Belongie S， Malik J， Puzicha J. Shape matching and object recognition using shape contexts[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2002，24(4):509-522.

[13] Cheeseman P， Smith R， Self M. A stochastic map for uncertain spatial relationships[C]∥Proceedings of the 4th International Symposium on Robotic Research. [S.l.]: IEEE， 1987:467-474.

[14] Li Y， Meng M Q， Liang H， et al. Particle filtering for WSN aided SLAM[C]∥Proceedings of IEEE/ASME International Conference on Advanced Intelligent Mechatronics. [S.l.]: IEEE， 2008:740-745.

[15] Zhou F， Torre F D L. Deformable graph matching[C]∥Proceedings of 2013 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). [S.l.]: IEEE， 2013，9(4):2922-2929.

[16] Bailey T， Nieto J. SLAM package of tim bailey[EB/OL]. [2013-10-21]. http://openslam.org/bailey-slam.html.

(责任编辑：李兵)

Graph Matching Algorithm for the Data Association Problem of Simultaneous Localization and Mapping in Ambiguous and Dynamic Environments

HUA Cheng-hao1， DOU Li-hua1， FANG Hao1， FU Hao2

(1.School of Automation， Beijing Institute of Technology， Beijing 100081， China; 2.College of Mechatronic Engineering and Automation， National University of Defense Technology， Changsha，Hu’nan 410073， China)

Proposed a graph matching approach RRW&SC to tackle the data association problem inherited in the SLAM. In our framework， the graph theory was utilized to build a mathematical model for data association firstly. Then the shape context feature was extracted for each node. Reweighted random walks was lastly adopted as the optimization engine to obtain the optimal solution for the graph model. The topology structure of the landmarks and the shape of the landmarks was used by RRW&SC algorithm， thus the geometric information of the environment was greatly enhanced which facilitates the data association. Simulation results show that， compared with traditional algorithms， the proposed data association algorithm can effectively handle a variety of complicated scenarios which might occur in SLAM， including enlarged observation noise， robot being kidnapped， or dynamic occlusion.

data association; graph matching;simultaneous localization and mapping (SLAM)

2015-09-28

北京市教育委员会共建专项资助项目(XK100070532)

华承昊(1983—)，男，博士生，E-mail:huachenghao@bit.edu.cn.

TP 242.6

A

1001-0645(2016)04-0405-07

10.15918/j.tbit1001-0645.2016.04.013