混合混沌多进制扩频系统的蒙特卡罗分析

郭淑霞，董文华，张磊，高颖

(1.西北工业大学 无人机特种技术国防重点实验室，陕西，西安 710065；2.西北工业大学 航海学院，陕西，西安 710072)



混合混沌多进制扩频系统的蒙特卡罗分析

郭淑霞1，董文华1，张磊1，高颖2

(1.西北工业大学 无人机特种技术国防重点实验室，陕西，西安 710065；2.西北工业大学 航海学院，陕西，西安 710072)

多进制扩频可以很好地提高通信抗干扰能力，但是其要求扩频码的数量要足够多，针对这一问题，提出了采用混沌映射序列的多进制扩频抗干扰方法. 针对单个低维混沌映射产生的混沌序列存在抗攻击能力差、密钥空间小、保密性不理想等缺点，产生了新的混合混沌序列，并且和基于m序列、Gold序列的传统直接扩展频谱系统的抗干扰能力进行对比. 仿真结果表明，混合混沌多进制扩频系统具有很好的抗干扰性(16进制混合混沌序列扩频系统抗干扰能力比传统直扩系统优10 dB)，且其解决了传统序列数量不足的问题.

混合混沌序列；多进制扩频；抗干扰；蒙特卡罗

传统直扩系统是一种有效的抗干扰通信体制，在军事通信中一直倍受关注，其抗窄带干扰性能好、可靠性高，但传信效率不高. 相比较，多进制扩频具有频谱利用率高、进入接收机前端的外部干扰少、抗多径能力强、传信速率快、码间串扰少和通信距离远等优点，是一种实现高效传信的有效途径[1]. 虽然多进制扩频通信效率高，但是它需要扩频码的数量要足够多. 传统的满足三值特性的m序列优选对很少，限制了m序列、Gold序列可用作扩频码的数量[2]，而混沌序列对初值很敏感，使其数量巨大. 因此，很多学者已将注意力集中到用混沌序列代替传统m序列、Gold序列等的研究上[3].

国内外关于混沌扩频系统已做了很多研究[4]，如：抗欺骗性和保密性. 但是在电子对抗中，衡量系统性能优劣的关键因素是它的抗干扰性. 作者发现国内对多进制扩频抗干扰方法的研究，大多都是基于传统伪随机序列的，还未有人研究采用混沌序列的多进制扩频的抗干扰方法.

鉴于此，本文研究了混沌多进制扩频抗干扰方法. 由于单个低维混沌映射产生的混沌序列抗攻击能力差、密钥空间小、保密性不理想等，因此作者将单个低维混沌映射产生的混沌序列组合产生了新的混合混沌序列，并仿真分析了其统计特性，再将混合混沌序列应用到多进制扩频系统中，不仅增强了系统的抗干扰能力，还解决了传统序列数量不足的难题.

1 混合混沌序列生成及其特性分析

1.1 混合混沌序列生成

单个低维混沌映射迭代产生的序列数量多，不但没有周期性，而且频谱宽、类随机、相关性好[5-7]. 然而，其存在抗攻击能力差、密钥空间小、保密性不理想等缺点. 因此，作者将单个低维混沌映射产生的混沌序列组合产生了新的混合混沌序列. 该序列由改进型Logistic映射和Chebyshev映射组成.

ω阶的Chebyshev映射定义为：

xn是当前时刻的状态，xn+1是下一时刻的状态. 分形参数ω≥2时，该映射具有遍历性和混沌性.

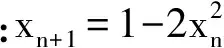
产生混合混沌序列的步骤如下：①Chebyshev映射迭代得到序列f1，将f1当作改进型Logistic映射的初值，得到序列f3；② 改进型Logistic映射迭代得到序列f2，将f2当作Chebyshev映射的初值，得到序列f4；③ 将序列f3和f4量化后进行异或最终获得混合序列f5. 图1所示为该混合混沌模型.

1.2 混合混沌序列统计特性

1.2.1 随机性分析

序列的随机性与信息的安全性成正比. 因此分析序列的随机性是很有意义的. 作者使用国际公认的FIPS PUB 140-2标准，检测混合混沌序列的随机性. 由FIPS PUB 140-2标准知，选取长为20 000的序列，可测试其单位、扑克、游程以及长游程. 选取5组由不同初始值得到的序列进行测试，表1即其测试结果.

表1 混合混沌序列FIPS PUB 140-2测试结果

由表1可知，5组任意的二值伪随机序列完全通过了FIPS PUB 140-2标准规定的4项测试，则该混合混沌映射序列具有很好的随机性.

1.2.2 平衡性分析

序列的不平衡会导致信息的载波泄露、传输的信息丢失、误码率增大. 因此，分析序列的平衡性也是很有意义的. 若文中产生的混合混沌序列中“-1”和“1”的数目分别是M和N，则其平衡度E=(M-N)/T，其中T为序列的码元总数.

以式(2)为依据，仿真分析文中生成的混合混沌序列的平衡性. 若ω=20，由图2平衡性曲线可知，该序列平衡度E<0.02，符合要求.

1.2.3 相关性分析

序列的相关性影响了扩频系统的通信误码率. 因此，其要求序列具有良好的相关特性. 图3仿真了ω=20，初值是0.32时序列的自相关特性；图4是序列初值分别取0.320 000 00、0.320 000 01时的互相关特性.

由图3、图4的仿真结果可知，该混合序列的相关特性很好，能很好地解决扩频系统的同步问题.

2 混合混沌多进制扩频抗干扰分析

2.1 AWGN干扰时系统性能

混合混沌多进制扩频中将输入速率是1/Tb的数据按k个比特进行分组，每个数据组(宽度为T0=kTb)选取混沌扩频序列集合(该集合由M=2k个相互正交的混沌扩频序列组成)中的一个码序列PN(t)作为发射序列，经过BPSK调制(为了方便，忽略脉冲成型)，形成发射信号：

(1)

式中：P为载波功率；ci(t)为扩频伪随机码PNi脉冲成型后波形信号. 其中扩频码集合包含了M个长度是N的扩频伪随机码{PN1，PN2，…，PNM}，且这M个伪随机码两两准正交. 发出信号经AWGN干扰后，最终接收到的信号可表示为

(2)

式中：τ为传输延迟；n(t)为均值等于0的AWGN. 经过数字正交下变频及低通滤波，并进行定时及载波同步后可以得到

(3)

那么相关器的输出为

(4)

(5)

由正交性可知，发送端码序列为PNi时，Ri才会很大. 其中，Vi，I(t)服从高斯分布，Ri(i=1，2，…，M)正确判决码的概率为

(6)

由文献[8]知:

(7)

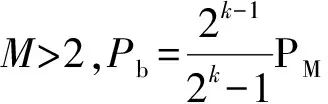
(8)

2.2 单频干扰下的性能

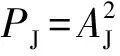
(9)

式中:R为信息传输速率；W为扩频序列带宽；TB为码元间隔；TC为扩频码片间隔；N为扩频码片个数. 由式(9)知单频干扰的功率被消减W/R.W/R即扩频系统的处理增益. 因此，单频干扰影响有用信号时，误码率近似为

(10)

2.3 脉冲干扰下的性能

(11)

当干扰机工作时，干扰功率远大于噪声功率，使噪声可以忽略，那么式(11)可以近似为

(12)

3 仿真结果与分析

采用蒙特卡罗的思想来仿真分析混合混沌多进制扩频系统抗干扰的能力，其基本原理是：首先将产生的随机信息序列串并转换，通过转换后的数据选择伪码序列，经过BPSK调制后，送到加有高斯白噪声(AWGN)的信道中，在接收端与多路伪码进行相关，寻找最大相关值的支路，确定伪码序列，并根据其对信息序列解扩、解调，进而获得最终信号. 最后将发送的信息和接收到的信息进行对比分析，计算出相对误码率. 仿真思路如图5所示. 下面主要仿真分析混合混沌多进制扩频系统的抗AWGN干扰和抗单频干扰能力.

信息速率相同时，采用m序列、Gold序列的扩频系统和采用混合混沌序列的多进制扩频系统的抗AWGN干扰和抗单频干扰能力相比结果分别如图6、图7所示.

由图6、7的结果可知，误码率为10-3时，2进制混合混沌序列扩频系统抗高斯白噪声干扰、抗单频干扰的能力与m序列、Gold序列扩频系统相差不大，4进制、8进制、16进制混合混沌序列扩频系统抗干扰能力分别比m序列、Gold序列扩频系统优5、8、10 dB.

4 结 论

文中将单个低维混沌映射产生的混沌序列组合产生了新的混合混沌序列，并将其应用到多进制扩频中，分析混合混沌多进制扩频的抗AWGN干扰和抗单频干扰能力. 通过仿真分析可知，该混合序列平衡性高、类随机、相关性好；且混合混沌多进制扩频比传统直扩系统的抗干扰能力更好，进制数越高抗干扰能力越强. 所以，使用混合混沌多进制扩频系统在提高信息传输效率、抗干扰能力的同时，满足了系统对扩频码数量的要求.

[1] 李瑞芳，李仁发.一种 Ad Hoc 网络信道接入退避算法及仿真分析[J].系统仿真学报，2007，19(1):141-144.

Li Ruifang，Li Renfa. Backoff algorithm and simulation for channel access in Ad Hoc networks[J]. Journal of System Simulation，2007，19(1):141-144. (in Chinese)

[2] 曾兴雯，刘乃安，孙献璞.扩展频谱通信及其多址技术[M].西安：西安电子科技大学出版社，2004.

Zeng Xingwen，Liu Naian，Sun Xianpu. Spread spectrum communication and its multiple access technology[M]. Xi’an: Xidian University Press，2004. (in Chinese)

[3] 王航，郭静波，王赞基.混沌多进制直接序列扩频信号的盲解扩[J].清华大学学报：自然科学版，2009，49(1)：14-16.

Wang Hang，Guo Jingbo，Wang Zanji. Chaotic M-ary direct sequence spread spectrum signals blind dispreading[J]. J Tsinghua Univ: Sci & Tech，2009，49(1):14-16. (in Chinese)

[4] 刘嘉兴，文吉.Ka频段混沌扩频测控系统的设想[J].电讯技术，2009，49(5)：33-37.

Liu Jiaxing，Wen Ji. Conception for a Ka-band chaotic spread spectrum TT&C system[J]. Telecommunication Engineering，2009，49(5):33-37. (in Chinese)

[5] Kohda Tohur，Tsuneda Akio. Pseudonoise sequences by chaotic nonlinear maps and their correlation properties[J]. IEICE Trans Commun，1993，E97 B (8):855-862.

[6] Li T Y，York J A. Period three implied chaos[J]. Amer Math Monthly ，1975，82(12):985-992.

[7] Rao Nini. A class of Chaotic spreading codes for A-CDMA system[J]. Journal of University of Electronic Science and Technology of China，2000，29(5):465-468.

[8] 樊昌信，曹丽娜.通信原理[M].6版.北京:国防工业出版社，2009.

Fan Changxin，Cao Lina. Principle of communication[M]. 6th ed. Beijing: National Defence Industry Press，2009. (in Chinese)

[9] 何世彪，谷诚，罗冬梅.混沌序列与Gold序列抗干扰性能仿真分析[J].计算机工程与设计，2011，32(2):623-727.

He Shibiao，Gu Cheng，Luo Dongmei. Performance simulation and analysis of anti-jamming of chaotic sequences and Gold sequences[J]. Computer Engineering and Design，2011，32(2):623-727. (in Chinese)

(责任编辑：刘芳)

Monte Carlo Analysis of Mixed Chaotic M-ary Direct Sequence Spread Spectrum System

GUO Shu-xia1，DONG Wen-hua1，ZHANG Lei1，GAO Ying2

(1.Science and Technology on UAV Laboratory，Northwestern Polytechnical University，Xi’an, Shanxi 710065，China;2.School of Marine Science and Technology，Northwestern Polytechnical University，Xi’an, Shanxi 710072，China)

M-ary direct sequence spread spectrum(DSSS) system does well in improving anti-jamming ability of communication，but it puts forward higher requirements to the spread spectrum code number. In order to solve this problem，M-ary DSSS anti-jamming scheme with chaotic mapping sequence was proposed. However，the chaotic sequence of single low-dimensional chaotic mapping has some shortcomings in terms of anti attack ability，key space and security. A new mixed chaotic sequence was presented，and the anti-jamming performance with traditional direct sequence spread spectrum system based onmsequence and Gold sequence was compared. Results of performance analysis and simulation indicate that the mixed chaotic M-ary DSSS system has strong anti-jamming(the anti-jamming ability of the 16-ary mixed chaotic direct sequence spread spectrum systems is 10 dB better than traditional DSSS systems)，and can meet the requirement for spread spectrum code number.

mixed chaotic sequences; M-ary DSSS; anti-jamming; Monte Carlo

2015-10-12

国家自然科学基金资助项目(61571368)；国防技术基础科研项目(2014607B006)

郭淑霞(1965—)，女，博士，副教授，E-mail:guoshuxia@sina.com.

董文华(1991—)，女，硕士生，E-mail:dongwenhua1022@sina.com.

TN 975

A

1001-0645(2016)07-0760-05

10.15918/j.tbit1001-0645.2016.07.019