湿式离合器接合过程摩擦振颤的影响因素

杨立昆，马彪，李和言

(北京理工大学 车辆传动重点实验室，北京 100081)



湿式离合器接合过程摩擦振颤的影响因素

杨立昆，马彪，李和言

(北京理工大学 车辆传动重点实验室，北京 100081)

针对湿式离合器在接合过程中的摩擦振颤问题，通过建立四自由度动力传动系统动力学模型及推导由摩擦效应引起的综合导入阻尼，基于特征值分析，获得系统的稳定性条件. 通过Matlab/Simulink仿真研究了摩擦因数、控制油压历程、转动惯量和传动轴刚度等对离合器摩擦振颤的影响.结果表明：由摩擦因数和控制油压历程决定的综合导入阻尼为负时，系统失去稳定性.同时，控制油压先快后慢的上升方式、增大离合器从动部分转动惯量及增加输出轴刚度均可不同程度地抑制摩擦振颤.

湿式离合器；摩擦振颤；综合导入阻尼；影响因素

湿式离合器是车辆传动系统的重要组成部件，其接合品质和使用寿命直接关系到传动系统的整体性能.在车辆起步和换挡过程中，湿式离合器可能出现摩擦引起的振颤现象.而摩擦振颤的发生会破坏离合器的接合稳定性，加速摩擦表面的磨损，进而造成离合器早期失效.

目前针对离合器摩擦振颤的研究相对较少，其主要理论来源于制动器的摩擦啸叫研究. 摩擦振颤是一种由摩擦引起的自激振动，其特性受到诸多外部因素的影响[1-2]. 与制动器啸叫不同，离合器摩擦振颤为低频振动，其频率范围大约为5～20 Hz[3]. 离合器的摩擦因数随主从动部分相对速度的变化被认为是引发摩擦振颤的主要原因. 基于特征值分析，不同学者得出一致结论，当摩擦因数随相对滑动速度呈负斜率变化时，离合器或制动器会产生不稳定的振动现象[4]. 而摩擦因数的变化并不是引发摩擦振颤的唯一因素，摩擦界面法向压力的变化会直接导致切向摩擦力的变化，进而也能够引起不稳定的摩擦振颤行为，这一理论在一些研究中也得到了证实[5-6].

文中通过建立4自由度动力传动系统动力学模型，基于特征值分析确定离合器综合导入阻尼对湿式离合器接合稳定性的影响，并通过Matlab/Simulink数值仿真，分析不同因素对离合器摩擦振颤的影响，为湿式离合器的优化提供理论依据.

1 离合器接合过程动力学模型

在起步和换挡过程中，车辆依靠离合器的滑摩实现动力的传递. 本文作者将动力传动系统简化为4自由度动力学模型分析离合器的接合过程，如图1所示. 其中J1为发动机与飞轮等效惯量，J2为离合器主动部分的等效惯量，J3为离合器从动部分及变速器于离合器从动部分之后的等效惯量，J4为变速器输出轴之后的传动环节及整车质量转换到输出轴的转动惯量.

(1)

式中：θ1，θ2，θ3，θ4分别为各惯量的绝对角位移；c1，c2，c3，c4为各部分的等效黏性阻尼；k12,k34分别为变速器输入轴和输出轴扭转刚度；Ti为发动机输出转矩；To为外部阻力矩；Tf为离合器摩擦转矩，可表达为

(2)

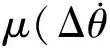
(3)

(4)

式中：a、b和c均为常数，主导控制油压历程；pmax为控制油压最大值.

2 基于综合导入阻尼的稳定性分析

(5)

(6)

式中：Tf0=Nμsp(t)Are，为离合器静摩擦转矩；cf=-Np(t)Areδ(μs-μk)，根据相应定义，cf可看作离合器滑摩过程综合导入阻尼，而该阻尼特性由摩擦因数特性和控制油压历程共同决定[8].

(7)

式中：A为系统矩阵；b为控制矩阵；u为输入向量；C为常数矩阵. 其中系统矩阵A一般用于分析系统的稳定性. 上述诸矩阵与向量的构成分别为

通常，系统的动态响应由自然响应与系统输入引起的响应所构成. 基于Lyapunov稳定性理论，对于线性定常系统，若系统矩阵A的所有特征值的实部均小于0，则系统稳定，其自然响应最终会趋于平衡状态；否则，只要存在一个实部大于0的特征值，系统将失去稳定性，即其自然响应会呈发散的趋势. 用于稳定性分析及后续仿真分析的系统参数主要基于某重型车辆通过等效计算而得，如表1所示.

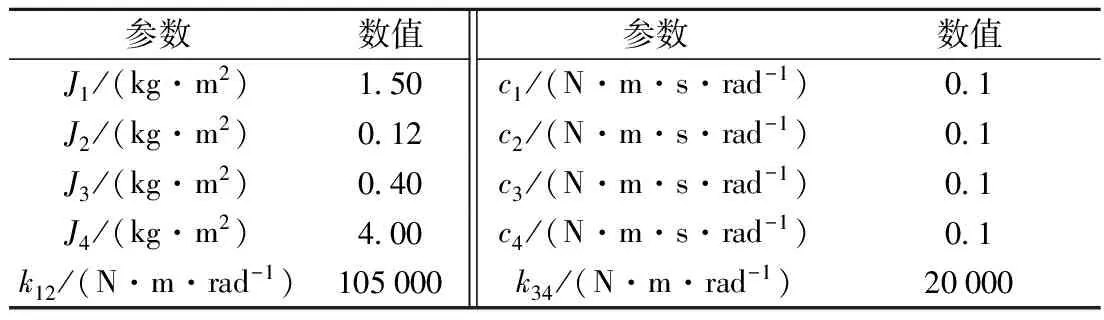
表1 稳定性分析及仿真所用相应参数

假设综合导入阻尼的变化范围为-15～15 N·m·s/rad，通过特征值分析获得系统稳定性与综合导入阻尼的关系如图2所示.

3 仿真与分析

基于Matlab/Simulink对前述的动力学模型进行仿真分析，仿真中离合器参数如下：摩擦副内径Ri为86 mm；外径Ro为125 mm；摩擦副数N为2；最大油压pmax为2.5 MPa，其它仿真条件和参数如下：

① 发动机输出转矩与转速的关系遵循某柴油机外特性，外部阻力矩To为500 N·m；

② 离合器主动部分初始转速为200 rad/s(约1 910 r/min)，从动部分初始转速为20 rad/s(约191 r/min)；

④ 假设控制油压变化历程有图3所示3种方式，初始零值代表摩擦副开始接触. 除特别说明，在后续的仿真计算中均采用油压历程1.

3.1 摩擦因数对离合器振颤的影响

根据综合导入阻尼的计算公式，摩擦因数是影响该值的主要因素之一. 为直观反映摩擦因数对离合器振颤的影响，将摩擦因数假设为以下3种情况：负斜率线性变化，即δ=0.01，如图4中情况2所示；保持不变，μ=0.15；正斜率线性变化，δ=-0.01，通过仿真获得离合器主从动部分角速度曲线如图5所示.

图中相同格式的曲线在相交前表明离合器尚未接合完成，上半部分表示离合器主动部分角速度，下半部分表示从动部分角速度；而当曲线相交时表明离合器接合完成，离合器主从动部分同速运转，其后各图含义均与此相同. 由图5可以发现仅当摩擦因数负斜率变化时，离合器出现明显的振颤行为. 因为当δ=0.01时，综合导入阻尼cf为负值，根据稳定性分析的结果，此时系统不稳定. 而在其它两种情况下，综合导入阻尼为零值或正值，系统保持稳定.

3.2 油压历程对离合器振颤的影响

除摩擦因数外，另一个影响综合导入阻尼的变量为控制油压. 为分析油压历程对离合器摩擦振颤的影响，本文构建了如图4所示的3种油压历程，不同的过程均在t=0.5 s时达到最大值. 此外，在湿式离合器实际运行过程中，摩擦因数多以式(6)所示的非线性形式变化，所以该部分同时分析了摩擦因数线性变化和非线性变化的振颤情况.

显然，与图6相比，在有振颤存在的情况，离合器角速度波动幅值更大，这主要因为摩擦因数线性变化时的负梯度更大；且在图7中，与油压历程1相比，在油压历程3的情况下，振颤显著加强. 其物理解释为：控制油压的变化速率直接关系到综合导入阻尼的变化速率. 而研究证明，离合器的摩擦振颤主要发生在接合后期[9]，这也能够从图中的曲线得到证实. 如果控制油压在后期的上升速率偏大，则导致综合导入阻尼也快速增大，造成系统不稳定加剧. 因此在离合器的控制油压历程的设计上应遵循先快速增加后缓慢增加的原则，这不但能够抑制离合器振颤，还能够有效缩短离合器接合时间，进而减少滑摩产生的热量.

3.3 转动惯量对离合器振颤的影响

可见随从动部分转动惯量增大，从动部分角速度波动明显减小，离合器振颤显著减弱. 进一步仿真表明，当两转动惯量J2与J3同比例增大时，从动部分角速度波动幅值也会减小，离合器振颤也能够得到改善. 但是根据离合器的设计准则，增加从动部分转动惯量会引发换挡过程冲击的增大. 所以从动部分转动惯量对离合器振颤和换挡冲击的影响是矛盾的.

3.4 传动轴刚度对离合器振颤的影响

4 结 论

建立了动力传动系统4自由度动力学简化模型，推导了离合器滑摩引起的综合导入阻尼，通过特征值分析确定当综合导入阻尼为负值时，系统失去稳定性. 当摩擦因数随相对滑动速度负斜率变化时，综合导入阻尼出现负值，离合器振颤发生，且摩擦因数线性负斜率变化时的振颤幅值大于摩擦因数非线性变化的情况. 当控制油压初始快速上升而后缓慢上升时，离合器振颤能够被一定程度地抑制，且离合器接合时间缩短. 离合器主动部分转动惯量和变速器输入轴刚度的变化对振颤的影响较小，但变速器输出轴刚度的增大可以减小离合器振颤的幅值. 此外，增大离合器从动部分转动惯量虽然可以有效地削弱其振颤的强度，但却会引起换挡冲击增强，所以在实际应用中增大从动部分转动惯量并不可行.

[1] Sinou J J，Jezequel L. Mode coupling instability in friction-induced vibrations and its dependency on system parameters including damping[J]. European Journal of Mechanics A/Solids，2007，26(1):106-122.

[2] Popp K，Rudolph M. Vibration control to avoid stick-slip motion[J]. Journal of Vibration and Control，2004，10(11):1585-1600.

[3] Centea D，Rahnejat H，Menday M. Non-linear multi-body dynamic analysis for the study of clutch torsional vibrations (judder)[J]. Applied Mathematical Modelling，2001，25(3):177-192.

[4] 胡宏伟，周晓军，杨先勇，等.离合器结合过程中抖动及其影响因素的分析[J].浙江大学学报(工学版)，2009，43(3)：535-539.

Hu Hongwei，Zhou Xiaojun，Yang Xianyong, et al. Analysis of clutch engagement judder and its influence factors[J]. Journal of Zhejiang University (Engineering Science)，2009，43(3):535-539. (in Chinese)

[5] Duan Chengwu，Singh R. Transient responses of a 2-dof torsional system with nonlinear dry friction under a harmonically varying normal load[J]. Journal of Sound and Vibration，2005，285(4-5):1223-1234.

[6] Duan Chengwu，Singh R. Influence of harmonically varying normal load on steady-state behavior of a 2dof torsional system with dry friction[J]. Journal of Sound and Vibration，2006，294(3):503-528.

[7] Astrom K J, Canudas-de-wit C. Revisiting the LuGre friction model[J]. IEEE Control Systems Magzine，2008，28(6):101-114.

[8] 陈俐，王昊松，习纲.离合器接合过程抖振机理与控制研究[J].系统仿真学报，2011，23(7)：1451-1458.

Chen Li，Wang Haosong，Xi Gang. Clutch engagement control based on stability analysis[J]. Journal of System Simulation，2011，23(7):1451-1458. (in Chinese)

[9] Ost W，De-baets P，Loccufier M，et al. Torsional vibrations of wet clutches: influence of mechanical parameters[J]. Meccanica，2010，45(3):341-353.

(责任编辑：孙竹凤)

Influence Factors of Friction-Induced Oscillation During Wet Clutch Engagement

YANG Li-kun，MA Biao，LI He-yan

(National Key Laboratory of Vehicle Transmission, Beijing Institute of Technology, Beijing 100081, China)

A simplified 4 degree-of-freedom (DOF) power-train dynamic model with an integrated damping induced by the friction effect of a wet clutch was developed to investigate the friction-induced oscillation (judder) during engagement, which may worsen the clutch engagement quality and result in the clutch failure. The stability criteria were obtained based on the eigenvalue analysis method. The numerical simulation in Matlab/Simulink was performed to evaluate the influence of different parameters such as the coefficient of friction, the variation process of control oil pressure, the moment of inertia of the clutch and the stiffness of drive shafts on the clutch judder. The results indicate that the system instability occurs when the integrated damping, which is determined by the coefficient of friction and the oil pressure, is negative. The results further show the clutch judder attenuates with the increase of the moment of inertia of the clutch driven component and the rise of the stiffness of the transmission output shaft. When the oil pressure rises rapidly at the early stage then followed by a slow rate, the amplitude of the friction-induced oscillation decreases.

wet clutch; friction-induced oscillation; integrated damping; influence factors

2014-12-04

国家自然科学基金资助项目(51175042)

杨立昆(1989—)，男，博士生，E-mail:maikiyang@bit.edu.cn.

马彪(1964—)，男，教授，博士生导师，E-mail:mabiao@bit.edu.cn.

TH 132.2

A

1001-0645(2016)07-0673-06

10.15918/j.tbit1001-0645.2016.07.003