基于改进奇异谱分析的信号去噪方法
2016-11-25戴豪民许爱强孙伟超
戴豪民,许爱强,孙伟超
(海军航空工程学院 飞行器检测与应用研究所,山东,烟台 264001)
基于改进奇异谱分析的信号去噪方法
戴豪民,许爱强,孙伟超
(海军航空工程学院 飞行器检测与应用研究所,山东,烟台 264001)
传统的去噪方法,比如小波阈值去噪,它只对高斯噪声有效,对于脉冲噪声却无能为力. 近年来发展起来的奇异谱分析方法可以在高信噪比的条件下很好地滤除上述两类噪声,但该方法降噪过程涉及了一定的主观因素,并且受矩阵扰动理论的限制,该方法随着信噪比的降低,去噪能力也随之下降. 针对上述情况,提出一种改进算法,将矩阵秩最小化理论应用于奇异谱分析方法中. 仿真结果表明,改进算法去噪效果明显,能够最大限度降低信号均方误差,提高信噪比,增强奇异谱分析方法的通用性.
奇异谱分析;奇异值分解;矩阵扰动理论;秩最小化理论
信号的产生、采集和传递都不可避免地会受到噪声的干扰,因此在信号预处理时进行去噪是十分必要的. 传统的去噪方法,比如基于谱分析的滤波器和小波去噪,先将原始信号从时域变换到频域,通过去除信号的某些频段成分的方法实现降噪. 通常,噪声表现为高频小幅值信号,信号通过低通滤波或小波阈值处理即可去除高频成分. 然而,有些情况下噪声的频带会分布在整个频率轴上,这样传统的方法就很难将有用信号和噪声的频谱区分开. 因此,传统方法具有一定的局限性. 近年来,在奇异值分解的基础上发展起来的奇异谱分析(singular spectrum analysis,SSA)技术已经应用于信号的去噪处理中[1],由于该技术独立于信号模型,并且具有不受噪声频谱分布影响的特点,所以能够达到自适应降噪的效果[2]. 但SSA亦有其不足之处,降噪过程涉及了一定的主观因素. 当原始信号受到轻微随机高斯噪声污染时,可以通过人为设定阈值,提取原信号轨迹矩阵的较大奇异值集合构成信号子空间,较小奇异值集合构成噪声子空间,实现信噪分离. 当原始信号被噪声严重污染,即使是极少数的大噪声,也会使该方法分析失效,尤其在复杂背景噪声环境中,噪声可能既包括轻微高斯噪声,又包括非平稳冲击噪声. 为此,针对SSA固有缺陷问题,本文提出一种改进SSA算法,将矩阵秩最小化理论应用于SSA中,实现信噪分离,增强SSA的通用性.
1 奇异谱分析
SSA是一种全局分析法,利用相空间重构的基本思想,通过奇异值分解以达到识别原始信号成份(如趋势、周期或准周期、噪声等)的目的[3]. 该方法包括分解和重构两个阶段,分解阶段包括嵌入操作和奇异值分解,重构阶段包括分组和对角平均化,其具体步骤如下:
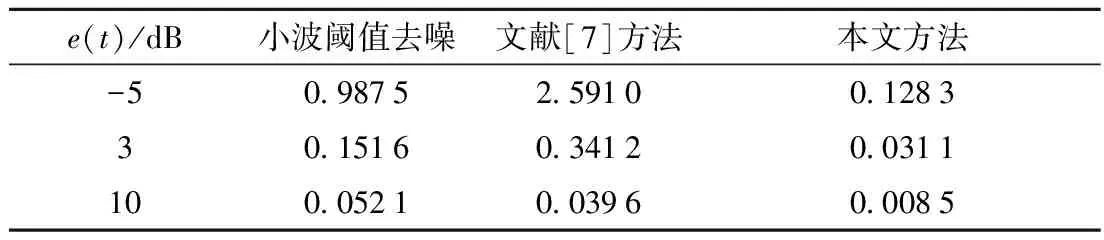
① 嵌入. 嵌入操作可以视为一维序列向多维序列的映射. 设长度为N的一维实序列FN=(f1,f2,…,fN),正整数L为滑动窗口长度,1 Xj=[fjfj+1… fj+L-1]T∈RL, 其中K=N-L+1,j=1,2,…,K. 映射的结果形成轨迹矩阵 X=[X1X2…XK]∈RL×K, 该轨迹矩阵是Hankel矩阵,可以表示为 (1) ② 奇异值分解. 对轨迹矩阵X进行奇异值分解,得到 (2) 其中d为X的非零奇异值个数,显然d=rank(X)≤min(L,M),λ1,λ2,…,λd为按降序排列的X的奇异值,Ui和Vi分别是X的左右奇异向量. ③ 分组. 分组的目的是分离信号中的加性成分. 如果对原始信号进行降噪处理,那么分组操作就是将原始序列FN构造的轨迹矩阵X表示成有用信号S和噪声E之和,即X=S+E. 在信号处理领域,通常认为前r(r (3) 2.1 窗口长度L的选择 上述SSA过程中,涉及到两个待定参数,即窗口长度L和重构信号的奇异值数目r. 由于窗口长度分别为L和K=N-L+1的轨迹矩阵奇异值分解是对称的,所以窗口长度L超过N/2是没有必要的. 同时,窗口长度L越大,序列的分解就会越精细,过小的L往往会造成序列中可解释的成分(如趋势、周期或准周期、噪声等)混杂在一起,不利于这些成分的提取[4]. 如果轨迹矩阵的秩远小于L,那么过大的L也是无意义,反而会增加奇异值分解的运算时间. 现实中不同信号轨迹矩阵的秩往往不同,但有用信号矩阵S往往是低秩的,即rank(S) 对于完全由噪声序列构成的矩阵E,往往是满秩矩阵,并且所有的奇异值相差较小,奇异值衰减较慢. 所以选择大的L往往可以挖掘出隐藏在原始信号中的噪声成分. 文献[5]从重构序列各成分的分离性和重构误差的角度上推荐L取序列长度N的中值(如果N为偶数,取L=N/2). 文献[6]研究了轨迹矩阵的奇异值随窗口长度L的变化规律,从理论上证明了当L取N的中值时,对应的奇异值会取得最大值,同时该文献也推荐在大多数情况下L取N的中值是最佳的选择. 2.2 奇异值数目r的选择 分组过程中,如何客观选取奇异值数目r进行重构信号,目前还没有通用方法. 相关文献的选择方法往往具有一定的主观性. 文献[7]提出奇异值均值法,即将所有低于奇异值平均值的奇异值置0,该方法只对原始信号受到轻微随机高斯噪声污染时有效,此时原始信号的轨迹矩阵前10%甚至1%的奇异值的和就占了全部奇异值之和的99%以上了,去掉一些较小的奇异值,就可以最大程度逼近有用信号矩阵,这也与主成分分析的思想一致. 文献[8]利用信号快速傅里叶变换(fastFouriertransform,FFT)结果中主频率个数确定奇异值数目,该方法只对平稳信号有效,对于非平稳信号,如果信号经过快速傅里叶变换后主频特征不明显或者被噪声频率淹没,那么就无法正确判定主频率个数. 尤其在复杂噪声背景下,上述这些方法就会失效,接下来本文从矩阵扰动理论角度阐述失效的原因. 设含噪序列FN=(f1,f2,…,fN),其加法模型可以表示为FN=SN+EN,SN为有用信号序列,EN为噪声序列,N为序列长度. 设正整数L为滑动窗口长度,1 (4) 假设噪声与有用信号统计不相关,则 XXT=SST+EET. (5) (6) 其中I为单位矩阵. 令rank(SST)=r≤L,如果SST的特征值分解为SST=UΛUT,U为特征向量,那么矩阵XXT的特征值分解可以表示为 XXT=UΛUT+σ2eI=U(Λ+σ2eI)UT=UΣUT. (7) (8) (9) 所以选择前r个奇异值逼近有用信号矩阵是合理的. 但是,在低信噪比情况下或者信号受到稀疏大噪声污染,虽然可以通过截断奇异值移除部分噪声,但仍有部分噪声对含噪矩阵前r个奇异值产生扰动,重构信号也将产生较大误差. 相关文献[10-11]指出高维的冗余数据本质上位于低维的子空间,这样的高维数据可以认为是稀疏的,其稀疏性表现在低秩性上,即可以通过计算数据矩阵X的最佳低秩矩阵S获得其最佳逼近. 在工程领域,潜在的低秩矩阵S可能被轻微噪声E所污染,也可能被稀疏大噪声W所污染. 当矩阵元素被严重破坏,传统方法已经不能有效从污染的数据中恢复出“干净”的数据. 受到压缩感知理论的启发,John Wright提出了鲁棒主成分分析(robust principal component analysis,RPCA)算法,并且证明了通过解优化问题就能够从被严重污染矩阵中精确恢复出所需的低秩矩阵[12]. 当数据矩阵有非常良好的结构,即低秩的,并且只有很少一部分元素被严重破坏,即噪声是稀疏的但大小可以任意,矩阵去噪(或矩阵恢复)可用如下优化问题来描述: (10) (11) 这样就将求解矩阵秩的非凸问题转换到凸优化问题,使得这个问题具有唯一解. (12) 目前,求解上述最优化问题有多种算法,如迭代阈值法[16](iterativethresholding,IT)、奇异值阈值法[17](singularvaluethresholding,SVT)、加速近端梯度法[18](acceleratedproximalgradient,APG)、精确增广拉格朗日乘子法[19](exactaugmentedLagrangemultiplier,EALM)以及非精确增广拉格朗日乘子法(inexactaugmentedLagrangemultiplier,IALM)等. 从各算法的时间开销和误差精度角度上比较,IALM法最佳[20]. 在仿真实验中,本文就是利用IALM法解决式(12)和(13)中的优化问题,算法的详细描述及收敛性证明请参见文献[19]. 综合上述分析,为去除信号中的噪声干扰,将秩最小化理论应用于SSA中实现去噪的步骤如下: ① 通过嵌入操作,将长度N的含噪序列FN=(f1,f2,…,fN)映射为轨迹矩阵 X=[X1X2…XK]∈RL×K, K=N-L+1,L=N/2. ② 根据模型(13),利用IALM算法恢复出低秩矩阵S. ③ 将低秩矩阵S对角平均化,转化成所需的长度为N的有用信号序列,最终实现信噪分离. 为了验证改进SSA去噪效果,本文分别采用原始SSA和小波阈值去噪方法与之进行对比. 此外,为了考察本文方法的适用性,以文献[20]的调幅调频信号为例,分别通过3个实验考虑3种背景噪声环境下的去噪效果,同时,采用信号均方误差(meansquareerror,MSE)和信噪比(signaltonoiseratio,SNR)来衡量各种方法的优劣,其定义形式如下: (13) (14) 实验1 考察以下仿真信号: 0.2sin10πt)+sin80πt+e(t). 式中,e(t)分别为信噪比是-5,3和10 dB的高斯白噪声,原始SSA算法采用文献[7]提出的奇异值均值法确定奇异值有效阶次. 信号采样频率为1 024 Hz,采样时间1 s,表1和表2是各种方法去噪后的MSE和SNR. 从这两个表中可以看出,在低信噪比情况下,小波阈值去噪和文献[7]方法都不能有效的滤除高斯白噪声;在中等信噪比情况下,这两种方法的去噪效果均有所改善,小波阈值去噪方法更好;在高信噪比情况下,3种方法都可以很好地去除掉高斯白噪声. 但上述3种噪声背景环境,本文方法表现俱佳. 表1 3种方法去噪后的信号MSE 实验2 考察以下仿真信号: 0.2sin10πt)+sin80πt+w(t). 表2 3种方法去噪后的信号SNR 其中,w(t)为随机添加的17个脉冲噪声. 原始SSA算法采用文献[8]提出的方法,该文献指出重构信号所需的奇异值个数是仿真信号功率谱主频数目的2倍,从图1可以看出,仿真信号功率谱的主频数目是2,所以本文采用前4个奇异值恢复原始干净信号. 表3是各种方法去噪后的信号MSE和SNR. 在稀疏大噪声背景环境下,本文方法表现特别优秀,几乎完全恢复干净信号,其误差精度可以忽略不计. 文献[8]方法也能滤除稀疏大噪声的干扰,其MSE和SNR与本文方法比均有明显劣势. 小波阈值去噪方法则不能去除掉这种脉冲噪声. 从图2也可以看出,文献[8]方法恢复出的信号已经出现失真,而小波阈值去噪方法中脉冲干扰依然存在. 表3 3种方法去噪后的信号MES和SNR 实验3 考察以下仿真信号: (1+sin5πt)cos(20πt+0.2sin10πt)+ 式中:e(t)为信噪比是-5 dB的高斯白噪声;w(t)为随机添加的17个脉冲噪声. 文献[20]提出对信号进行中值滤波可以有效抑制脉冲干扰,原始SSA算法采用文献[20]和文献[8]相结合的方法,首先对信号进行中值滤波,然后采用FFT确定信号主频个数以及奇异值数目. 从图3可以看出,中值滤波后信号功率谱的主频数目是2,所以本文采用前4个奇异值恢复干净信号. 表4是各种方法去噪后的MES和SNR. 在这种复杂噪声背景环境中,中值滤波和FFT相结合的方法去噪效果较好,中值滤波起到了抑制脉冲干扰的作用,但中值滤波也会使信号变得更为光滑,从图4可以看出,该方法恢复出的信号与原始干净信号相比失真明显. 小波阈值去噪方法只对高信噪比的高斯白噪声有效,对于脉冲干扰几乎没有效果. 表4 4种方法去噪后的信号MES和SNR 复杂的噪声背景环境中,信号往往既被高斯噪声污染,又被脉冲噪声污染,传统的去噪方法比如小波阈值去噪只对高斯噪声有效,对于脉冲干扰却无能为力. 原始SSA方法结合中值滤波能够对脉冲噪声起到一定的抑制作用,但同时也会使原始信号严重失真. 本文将矩阵秩最小化理论应用于SSA中,从仿真结果上看,去噪效果明显,能够最大限度的降低信号均方误差,提高信噪比尤其对脉冲噪声,几乎可以完全实现信噪分离. 此外,由于仿真实验仅仅以高斯白噪声为参考,未涉及其他噪声类型的去噪效果,所以这也是本文下一步研究方向. [1] Hassani H,Mahmoudvand R,Zokaei M,et al. On the separability between signal and noise in singular spectrum analysis[J]. Fluctuation and Noise Letters,2012,11(2):1-11. [2] Zhigljavsky A. Singular spectrum analysis for time series: introduction to this special issue[J]. Statistics and Its Interface,2010,3(3):255-258. [3] Golyandina N,Zhigljavsky A. Singular spectrum analysis for time series[M]. [S.l.]: Springer,2013. [4] Hassani H,Mahmoudvand R,Zokaei M. Separability and window length in singular spectrum analysis[J]. Comptes Rendus Mathematique,2011,349(17):987-990. [5] Golyandina N. On the choice of parameters in singular spectrum analysis and related subspace-based methods[DB/OL]. [2010-07-20].http://arxiv.org/abs/1005. 4374. [6] Mahmoudvand R,Zokaei M. On the singular values of the Hankel matrix with application in singular spectrum analysis[J]. Chilean Journal of Statistics,2012,3(1):43-56. [7] 王益艳.基于特征均值的SVD信号去噪算法[J].计算机应用与软件,2012,29(5):121-123. Wang Y Y. Mean value of eigenvalue-based SVD signal denoising algorithm[J]. Computer Applications and Software,2012,29 (5) :121-123. (in Chinese) [8] 钱征文,程礼,李应红.利用奇异值分解的信号降噪方法[J].振动,测试与诊断,2011,31(4): 459-463. Qian Zhengwen,Cheng Li,Li Yinghong. Signal denoising method by means of SVD[J]. Journal of Vibration Measurement & Diagnosis,2011,31(4):459-463. (in Chinese) [9] Stewart G W. Perturbation theory for the singular value decomposition[R]. College Park: Computer Science Department,University of Maryland,1998. [10] Candès E J,Tao T. The power of convex relaxation: Near-optimal matrix completion[J]. IEEE Transactions on Information Theory,2010,56(5):2053-2080. [11] Candes E J,Plan Y. Matrix completion with noise[J]. Proceedings of the IEEE,2010,98(6):925-936. [12] Wright J,Ganesh A,Rao S,et al. Robust principal component analysis: exact recovery of corrupted low-rank matrices via convex optimization[C]∥The Twenty-Fourth Annual Conference on Neural Information Processing Systems. Vancouver:[s.n.],2009:2080-2088.[13] Candès E J,Li X,Ma Y,et al. Robust principal component analysis?[J]. Journal of the ACM ,2011,58(3):1101-1137. [14] 彭义刚,索津莉,戴琼海,等.从压缩传感到低秩矩阵恢复:理论与应用[J].自动化学报,2013,39(7):981-994. Peng Y G,Suo J L,Dai Q H,et al. From compressed sensing to low-rank matrix recovery: theory and applications[J]. Acta Automatica Sinica,2013,39(7):981-994. (in Chinese) [15] Zhou Z,Li X,Wright J,et al. Stable principal component pursuit[C]∥Proceedings of the IEEE International Symposium on Information Theory. Austin: IEEE,2010:1518-1522. [16] Ganesh A,Lin Z,Wright J,et al. Fast algorithms for recovering a corrupted low rank matrix[C]∥The third IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing. Radisson, Aruba: IEEE,2009:213-216. [17] Cai J F,Candès E J,Shen Z. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal on Optimization,2010,20(4):1956-1982. [18] Toh K C,Yun S. An accelerated proximal gradient algorithm for nuclear norm regularized linear least squares problems[J]. Pacific Journal of Optimization,2010,15(6):615-640. [19] Lin Z,Chen M,Ma Y. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices[DB/OL].2010-09-26. http:// arXiv preprint arXiv: 1009.5055. [20] 徐锋,刘云飞.基于中值滤波-奇异值分解的胶合板拉伸声发射信号降噪方法研究[J].振动与冲击,2011,30(12):135-140. Xu Feng,Liu Yunfei. Noise reduction of acoustic emission signals in a plywood based on median filtering-singular value decomposition[J]. Journal of Vibration and Shock,2011,30(12):135-140. (in Chinese) (责任编辑:刘芳) Signal Denoising Method Based on Improve Singular Spectrum Analysis DAI Hao-min,XU Ai-qiang,SUN Wei-chao (Institute of Aircraft Detection and Application,College of Naval Aeronautical and Engineering,Yantai,Shandong 264001,China) The traditional denoising method,such as wavelet threshold,is only valid for Gaussian noise,but is powerless for pulse jamming. Singular spectrum analysis developed in recent years can be a good filter at high SNR conditions of these two types of noises,but the process of noise reduction involves a certain subjective factors,and is subject to restrictions of matrix perturbation theory. Moreover,the ability of denoising will decrease with the lower SNR. For the above situation,an improved algorithm was proposed,which applied rank minimization theory to singular spectrum analysis. Simulation results show that denoising effect of the improved algorithm is obvious,which can maximize the reduction of the mean square error of the signals and improve signal to noise ratio; enhance versatility of singular spectrum analysis. singular spectrum analysis; singular value decomposition; matrix perturbation theory; rank minimization theory 2014-04-01 国家部委预研基金资助项目(9140A27020212JB14311) 戴豪民(1982—),男,博士生,E-mail:daihaomin521@163.com. 许爱强(1963—),男,教授,博士生导师,E-mail:1397245858@qq.com. TH 911 A 1001-0645(2016)07-0727-07 10.15918/j.tbit1001-0645.2016.07.013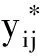
2 SSA的参数选择
3 矩阵扰动理论
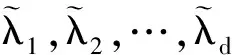
4 基于秩最小化理论的去噪方法
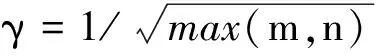
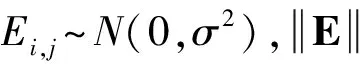
5 仿真实验




6 结 论
