基于频率步进的宽带分布式全相参雷达
2016-11-25殷丕磊闫路张宗傲杨小鹏曾涛
殷丕磊,闫路,张宗傲,杨小鹏,曾涛
(北京理工大学 信息与电子学院,北京 100081)
基于频率步进的宽带分布式全相参雷达
殷丕磊,闫路,张宗傲,杨小鹏,曾涛
(北京理工大学 信息与电子学院,北京 100081)
系统时间同步是宽带分布式全相参雷达的核心问题之一,但现有的时间同步技术无法满足其同步精度需求. 本研究基于频率步进信号提出了一种宽带分布式全相参雷达时间同步方法. 分析了时间同步误差对系统相参性能的影响;提出了采用频率步进信号代替线性调频信号的时间同步方法. 理论分析表明,该方法能够极大地减小时间同步误差对相参性能的影响,进而降低对时间同步精度的需求;通过仿真分析验证了本方法的有效性.
分布式全相参;步进频;时间同步误差;宽带
分布式全相参雷达是一种新体制雷达,被认为是下一代雷达的发展方向,它由多部可独立工作的小口径单元雷达和一部中心控制机组成,通过对单元雷达进行信号级的融合处理,能够实现多部雷达的孔径相参,从而达到等效大口径雷达的性能[1]. 一个由N部单元雷达组成的分布式全相参雷达系统,在全相参工作模式下可以获得N3倍于单部雷达的输出SNR增益[2]. 因此,分布式全相参雷达可代替传统大口径雷达,以解决其机动部署能力差、造价成本昂贵、器件制造工艺要求高等问题.
美国林肯实验室在2003年首先提出了分布式孔径全相参雷达的概念[3],并于2004年发表了分布式全相参雷达的年度研究报告,对其组成、原理及相参参数估计等问题进行了介绍[1]. 在此基础上,林肯实验室于2004年和2005年,分别在空军实验室及白沙导弹靶场,对由2部单元雷达组成的分布式全相参雷达的性能开展了实验验证,针对不同目标均取得了良好的结果[4-5]. 鉴于分布式全相参雷达的潜在优势和应用前景,目前,国内已逐步开展了相关的研究,其中,中国航天科工集团2院23所已开展了分布式全相参合成原理的验证试验[6]. 国内外的研究工作多集中在窄带分布式全相参雷达以及分布式全相参雷达原理的验证,然而,在宽带分布式全相参雷达中,各单元雷达的时间同步误差将导致时间差估计出现偏差,从而降低分布式全相参雷达的相参性能.
本文针对宽带分布式全相参雷达的时间同步问题,首先建立了时间同步误差的数学模型,分析了目标处两雷达信号的时间差和相位差. 针对时间差估计问题,分别提出了基于正交信号和基于相参信号的时间差估计方法. 分析了时间同步误差对系统相参性能的影响,指出了相参性能与脉压后的脉冲宽度有关. 因此,提出了采用频率步进信号代替线性调频宽带信号,利用频率步进信号的瞬时窄带特性减小时间同步误差对相参性能的影响,从而降低宽带系统的时间同步精度需求,使宽带系统的时间同步精度可实现[7].
1 时间同步误差的影响分析
为实现分布式全相参雷达的全相参工作,首先需要对目标处各单元雷达发射信号的时间差和相位差进行估计. 然后通过调整发射信号的发射时刻以及初始相位,以保证各单元雷达信号能够在目标处同时同相叠加以实现发射相参. 最后,对接收信号进行时延和相位的调整以实现接收相参,从而最终实现全相参.
然而,时间同步误差将影响时间差的估计精度,从而降低分布式全相参雷达的性能,下面分析时间同步误差对分布式全相参雷达相参性能的影响.
1.1 时间同步误差模型
在分布式系统中,由于各单元雷达分散布设且使用不同的时钟源,因此各单元雷达的时钟源会存在时间同步误差. 文中,为了简化表达,以两部单元雷达构成的分布式全相参雷达为例进行介绍. 两单元雷达的时间同步误差可以表示为
(1)
式中:ΔEa,Δf,ΔK分别表示两时钟源的初始时钟差、频率偏差、频率漂移率差;Δε(t)表示由噪声引起的两雷达的时间差. 则目标处两信号的时间差和相位差[8]分别为
(2)
(3)
式中:f0为发射信号的载频;t1=R1/c;t2=R2/c;R1、R2分别为两单元雷达与目标的距离;c为电磁波的传播速度.
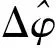
1.2 时间差的估计方法
为了实现系统的全相参工作,需估计目标处的时间差. 因此,分别提出了基于正交信号和相参信号的两种时间差估计方法.
1.2.1 基于正交信号的时间差估计方法
在接收相参工作模式下,各单元雷达发射正交信号. 利用正交信号的可分离性,在同一雷达上可分别获得单基地回波和双基地回波,从而得到时间差的估计值. 两单元雷达发射的正交信号可分别设为
(4)
(5)
式中:u1(t)=rect(t/τ),u2(t)=rect((t-Δτ)/τ)分别表示两正交信号的包络;s1(t),s2(t)为正交编码信号. 理想正交信号满足:
(6)
式中xcorr(,)表示对两信号做互相关运算. 单元雷达1、2接收到的目标回波信号分别为
y1(t)=x1(t-2t1)+x2(t-t1-t2),
y2(t)=x1(t-t1-t2)+x2(t-2t2).
利用两单元雷达的发射信号x1(t)、x2(t)作为每个单元雷达两路通道的匹配滤波器冲激响应,对回波信号分别进行匹配滤波. 在单元雷达1,两个匹配滤波器均以单元雷达1的时钟源为基准,分别为x1(t)和x2(t+Δτ). 因此,在雷达1处得到两路回波信号分别为
(7)
(8)
利用两路信号的峰值所对应的时刻估计时间差:
(9)
式中tmax(y)表示y取得最大值的时刻.
相同的,在单元雷达2,两个匹配滤波器分别为x1(t-Δτ)和x2(t),得两路回波信号分别为
(10)
(11)
得时间差估计值:
(12)
最后,为降低随机噪声的影响,对两估计值式(9)和式(12)进行加权处理得时间差的最终估计值:
(13)
通过比较式(13)与式(2)可知,该方法能够实现时间差的理想跟踪. 基于正交信号的时间差估计方法如图1所示.
1.2.2 基于相参信号的时间差估计方法
利用接收相参工作模式下得到的时间差估计值式(13)以及相位差式(3)对发射信号进行时延和相位调整,可实现目标处两相参信号的相参叠加,设叠加信号为
(14)
式中:A表示叠加信号的幅度;E表示叠加信号的起始时刻;θ为叠加信号的初始相位.
此时,单元雷达1、2接收到的回波信号(下变频后)分别为
单元雷达1、2的匹配滤波器单位冲激响应分别为
H1(t)=rect(-t/τ),H2(t)=rect(-(t+Δτ)/τ).
在两单元雷达上,对回波信号进行匹配滤波输出Z1(t)、Z2(t). 利用两路匹配滤波输出信号峰值处对应的时刻估计时间差:
(15)
通过比较式(15)与式(2)可知,由于时间同步误差Δτ的存在,导致时间差估计值存在估计偏差2Δτ. 基于相参信号的时间差估计方法如图2所示.
1.3 时间同步误差对相参性能的影响
由前面的分析可知,时间同步误差Δτ导致时间差估计值存在偏差,将会降低分布式全相参雷达的相参性能. 本节分析时间同步误差对相参性能的影响.
一般地,在宽带分布式全相参系统中,采用线性调频信号作为两单元雷达的发射信号:
(16)
(17)
式中:u1(t)=rect(t/τ)ejk1πt2,u2(t)=u1(t-Δτ)分别为两信号的复包络;τ为脉冲宽度;k1=B/τ为调频斜率,B为信号带宽;f0为信号起始频率.
首先,为了使两雷达的发射信号在目标处相参叠加,利用时间差估计值式(15)和相位差式(3)对雷达2的发射信号进行时延和相位的调整:
(18)
此时,单元雷达1、2接收到的回波信号(下变频后)分别为Y1(t),Y2(t).
然后,为了实现接收相参,对单元雷达2的接收信号进行时延和相位的调整:
(19)
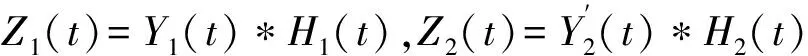
其中,运算“*”表示卷积运算.
最后,将两单元雷达的输出相叠加得到系统全相参输出为
(20)
式中τ′=1/B为脉压后的脉冲宽度. 从式(20)可以看出,时间同步误差Δτ导致全相参输出的两脉冲间存在2Δτ的时间差,从而导致能量损失. 定义由时间同步误差Δτ所引起的能量损失比LΔτ为
(21)
图3为能量损失比的仿真结果,其中,横坐标“时间同步误差”是以脉压后的脉冲宽度进行了归一化处理.
从仿真图中可以看出:
① 能量损失比随时间同步误差的增大而增大. 若要求分布式全相参雷达的能量损失比小于0.3 dB,则时间同步误差应小于0.065τ′,对于带宽为256 MHz的宽带系统,要求时间同步误差应小于0.27 ns,如此高的时间同步精度对于现有的同步技术是难以实现的;
② 当两单元的时间同步误差取值一定时,系统脉压后脉冲宽度(τ′)越大,能量损失比越小,即系统的相参性能与脉压后的脉冲宽度有关.
2 基于频率步进的分布式全相参雷达
为了减小时间同步误差对相参性能的影响,提出采用频率步进信号代替线性调频信号作为宽带分布式系统的发射信号,利用频率步进信号的瞬时窄带对时间同步误差的鲁棒特性降低系统的时间同步精度需求,从而使宽带分布式全相参雷达的时间同步工程可实现. 采用调频步进信号作为两单元雷达的宽带发射信号:
(22)
(23)
式中:u1(t)=rect(t/τ)ejk2πt2,u2(t)=u1(t-Δτ)分别为两频率步进信号的复包络;τ为发射子脉冲宽度;N为频率步进点数;Tr为脉冲重复周期;k2=Bτ/τ为子脉冲调频斜率;Bτ为子脉冲带宽;f0为调频步进信号的起始频率;Δf为频率步进阶梯.
为了使两雷达的发射信号在目标处同时同相叠加,对雷达2的发射信号进行时延和相位调整:
(24)

(25)
(26)
为了保证两雷达接收信号能同时同相叠加实现接收相参,对单元雷达2的信号进行时延和相位的调整:
(27)
将时间差估计值式(15)以及相位差分别代入式(25)和式(27),得
(28)
(29)
首先在两单元雷达上分别对回波信号的子脉冲进行快时间维的匹配滤波处理,然后将两单元雷达的滤波结果相加实现两单元雷达的相参叠加,最后进行慢时间维等距离采样点IFFT,并利用一定的抽取和拼接算法获得分布式全相参雷达的目标一维距离像.
单元雷达1、2的子脉冲匹配滤波器的冲激响应分别为
因此,在两单元雷达上,频率步进信号的子脉冲脉压输出分别为
将两单元雷达的匹配滤波器输出信号相加得
(30)
式中τ″=1/Bτ为脉压后的子脉冲宽度. 最后,对信号Z(t)进行脉间IFFT处理,然后进行目标的抽取和拼接,从而得到目标的一维高分辨距离像.
从式(30)可以看出,时间同步误差Δτ导致频率步进信号的子脉冲之间有2Δτ的时间差,从而降低系统的相参性能. 利用第2节的分析可以得出,若要求能量损失比小于0.3 dB,则时间同步误差应小于0.065τ″=0.065/Bτ≈N0.065/B. 因此,采用频率步进信号可以降低宽带系统的时间同步精度需求,恰当选择合适的步进点数N,可使宽带分布式系统的时间同步工程可实现.
3 仿真结果与分析
本节仿真验证频率步进信号对时间同步误差的鲁棒性. 设目标与雷达1的距离R1=10 km,线性调频信号参数及调频步进信号参数如表1和表2所示.
表1 线性调频信号参数
Tab.1 Parameters of linear frequency modulated (LFM) signal

参数取值参数取值起始频率f0/GHz1信号带宽B/MHz256脉冲宽度τ/μs10脉冲重复周期Tr/ms01

表2 调频步进信号参数
首先,设置时间同步误差Δτ=0.3τ′=0.3/B=1.2 ns,分别得到线性调频信号和频率步进信号的目标距离像,如图4所示. 从仿真结果中可以看出,在相同时间同步误差的情况下,频率步进信号的目标距离像幅度高于线性调频信号的目标距离像幅度;而且,线性调频信号的输出目标距离已经严重偏离了目标的真实距离. 仿真结果说明在相同的时间同步误差条件下,频率步进信号的相参性能高于线性调频信号的相参性能,即频率步进信号对时间同步误差具有鲁棒性.
然后,仿真能量损失比受时间同步误差的影响,仿真结果如图5所示. 从仿真图中可以看出,频率步进信号和线性调频信号的能量损失比均随着时间同步误差的增大而增大,当时间同步误差大于0.295τ′=1.15 ns时,线性调频信号的能量损失比趋于-6 dB,说明此时全相参雷达的输出幅度趋于单部雷达的输出幅度,即分布式全相参雷达相对于单部部雷没有性能的提高,因此该情况应予以避免. 若要求能量损失比小于0.3 dB,采用线性调频信号时需时间同步误差小于0.065τ′=0.27 ns,而采用频率步进信号时仅需时间同步误差小于4τ′=15.6 ns,时间同步精度指标放宽了约62倍(近似等于步进点数). 因此,仿真结果表明,频率步进信号能够降低宽带系统的时间同步精度需求,从而使宽带分布式全相参雷达的时间同步工程可实现.
4 结 论
在宽带分布式全相参雷达系统中,时间同步误差严重降低了系统的相参性能,然而现有同步技术难以满足宽带系统的时间同步精度需求,从而限制了宽带分布式全相参雷达的应用.
本文在分析时间同步误差对分布式全相参雷达相参性能影响的基础上,利用分布式全相参雷达的相参性能与脉压后脉冲宽度的关系,提出了基于频率步进信号的宽带分布式全相参雷达时间同步方法,从而降低了宽带系统的时间同步精度需求,使宽带分布式全相参雷达的时间同步精度达到工程可实现的水平. 仿真结果验证了所提方法的有效性. 本文的研究将为分布式全相参雷达的实现奠定一定的理论基础.
[1] Cuomo K M,Coutts S D,McHarg J C,et al. Wideband aperture coherence processing for next generation radar(NexGen)[R]. [S.l.]: MIT Lincoln Laboratory,2004:11-16.
[2] Fletcher A S,Robey F C. Performance bounds for adaptive coherence of sparse array radar[C]∥Proceedings of 11th Conference Adaptive Sensors Array Processing. Lexington,MA:[s.n.],2003.
[3] Ahlgren G W. Next generation radar concept definition team final report[R]. [S.l.]: MIT Lincoln Laboratory,2003.
[4] Coutts S D,Cuomo K M,McHarg J C,et al. Distributed coherent aperture measurements for next generation BMD radar[C]∥Proceedings of Fourth IEEE Workshop on Sensor Array and Multichannel Processing. Waltham,MA:[s.n.],2006:390-393.
[5] Brookner E. Phased-array and radar astounding breakthroughs-an update[C]∥Proceedings of IEEE Radar Conference. Rome,Italy:[s.n.], 2008:1-6.
[6] 曹哲,柴振海,高红卫,等.分布式阵列相参合成雷达技术研究与试验[J].现代防御技术,2012,40(4):1-11.
Cao Zhe,Chai Zhenhai,Gao Hongwei,et al. Technology and tests on distributed aperture coherence-synthesizing radar[J]. Modern Defence Technology,2012,40(4):1-11. (in Chinese)
[7] Yang Xiaopeng,Yin Pilei,Zeng Tao. Time and phase synchronization for wideband distributed coherent aperture radar[C]∥Proceedings of 2013 IET International Radar Conference. Xi’an,China:[s.n.], 2013:638-642.
[8] 殷丕磊,杨小鹏,曾涛.分布式全相参雷达的相位差跟踪技术[J].信号处理,2013,29(3):313-318.
Yin Pilei,Yang Xiaopeng,Zeng Tao. Tracking technology of phase difference for distributed aperture coherent radar[J]. Signal Processing,2013,29(3):313-318. (in Chinese)
[9] Yang Xiaopeng,Yin Pilei,Zeng Tao,et al. Phase difference estimation based on orthogonal signals for distributed coherent aperture radar[C]∥Proceedings of 2013 International Conference on Radar. Adelaide,Australia: [s.n.],2013:576-580.
(责任编辑:刘芳)
Wideband Distributed Coherent Aperture Radar Based on Step Frequency Signal
YIN Pi-lei,YAN Lu,ZHANG Zong-ao,YANG Xiao-peng,ZENG Tao
(School of Information and Electronics,Beijing Institute of Technology,Beijing 100081,China)
The time synchronization is the key issue of wideband distributed coherent aperture radar. However,current time synchronization technology could not meet the requirement of high accuracy of time synchronization for wideband distributed coherent aperture radar. In this paper,a time synchronization method based on step frequency signal was proposed. Firstly,the impact of time synchronization error on coherent performance was investigated. And then,a time synchronization method by using step frequency signal to replace linear frequency modulated signal was proposed. According to theoretical analysis,the effect of time synchronization error on coherent performance was reduced in our proposed method,which reduced the requirement of time synchronization accuracy into a realizable level. At last,the effectiveness of proposed method was verified by simulations.
distributed coherent aperture radar; step frequency signal; time synchronization error; wideband
2015-02-10
国家自然科学基金资助项目(61001198,61225005,61120106004,61301189)
殷丕磊 (1987—),男,博士生,E-mail:yinpilei@gmail.com.
杨小鹏(1976—),男,副教授,博士生导师,E-mail:xiaopengyang@bit.edu.cn.
TN 957.2
A
1001-0645(2016)07-0749-06
10.15918/j.tbit1001-0645.2016.07.017
