一种矩量法精度分析验证方法研究

刘燕婻，潘小敏，盛新庆

(北京理工大学 信息与电子学院，北京 100081)



一种矩量法精度分析验证方法研究

刘燕婻，潘小敏，盛新庆

(北京理工大学 信息与电子学院，北京 100081)

提出一种针对任意形状目标散射矩量法计算的精度验证方法. 根据等效原理，建立介质目标积分方程. 令介质分界面两侧的介质参数相同，推导出入射等效源在介质体外产生的场为0. 利用这种性质，对任意形状目标散射问题矩量法计算精度进行验证. 对球和正8面体等算例进行的数值实验，验证了不同奇异点处理方法下介质目标积分方程的精度. 数值实验证明了转移法和坐标变换法的精度优于提取法. 结果同时表明所提出验证方法的有效性和通用性.

矩量法；精度；奇异点

基于积分方程的矩量法广泛应用于电磁计算. 理论上讲，积分方程的建立过程没有任何近似，这保证了矩量法的精度. 从算法设计过程看，使用局域基函数来离散积分方程需要对目标进行剖分. 对面积分方程，剖分单元既可以是平面三角形、四边形及其组合，也可以是曲面的三角形、四边形及其组合. 无论采用哪种剖分单元，都会在矩量法的离散过程中引入一些误差. 更重要的是，当场源重合时，矩阵元素的计算会出现奇异积分，奇异点的处理对矩量法的精度有重要影响[1-3]. 如何进行精度分析，是矩量法研究的一个非常重要的方面. 对于有解析解的目标，例如球，可以将计算结果与解析解进行比较，验证矩量法的精度. 而对于复杂目标，则没有一种统一方法对矩量法精度进行验证. 目前普遍的方法是将数值解与实验测量值，或其他算法及商业软件计算结果进行比较. 显然，这种方法本身存在很多局限. 近年来，Ergül等[4]提到使用入射等效源不辐射的性质来验证算子的精度. 在这一思想的基础上，本文提出一种验证任意目标矩量法计算精度的方法，并将其用于验证不同奇异点处理方式的精度.

1 验证原理和方法

均匀媒质中的矢量波动方程为

(1)

(2)

并矢格林函数满足

××(r，r′)-k2(r，r′)=δ(r-r′).

(3)

假定某一均匀媒质中，k为常数. 区域V2被区域V1包围，S为V2的边界，V1和V2内部各有一个电流源J1和J2，如图1所示.

(4)

其中

(5)

(6)

对式(4)左边使用第二类矢量格林定理

(7)

(8)

V1中的总场E为V1中的电流源J1和V2中的电流源J2分别所产生的场的叠加. 而式(8)表明，E也可以表示为V1中的电流源J1与边界S上的一组等效源(Js，Ms)产生的场的叠加. 这样(Js，Ms)产生的场恰好代表了J2在V1中的场，这被称作是等效原理.

求解介质目标的散射，可以使用等效原理来建立方程. 设V1中介质参数为(ε1，μ1) ，V2中为(ε2，μ2).V1中的总场由入射场(E1，H1)与散射场(Es，Hs)叠加而成，即

(9)

(10)

则等效源(Js，Ms)可以分成两部分，分别称为入射等效源和散射等效源.

(11)

(12)

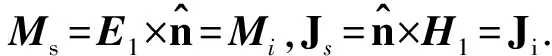
由此，式(8)化为

(13)

式(13)表明入射等效源在介质体外产生的场为0. 使用这一性质，就可以考察矩量法离散所产生的误差.

以均匀介质体的面积分方程CTF为例：

(14)

(15)

其中L和K算子定义为

(16)

(17)

(18)

令ε1=ε2，μ1=μ2，求解方程(14)和(15)得到入射等效源(Ji，Mi)的展开系数，并由此求得(Ji，Mi)在远处所产生的场值. 如取181个观察点，远场的均方根(RMS)可以按照下式进行计算为

(19)

从上面的分析中看到，在介质体外部Ji和Mi不应辐射，所以从式(19)中计算得到的RMS的值就直接反映了计算的均方根误差.

2 奇异点处理方法及数值算例

2.1 奇异点处理方法

在矩量法中，当场点和源点相距较近时，矩阵元素计算涉及到的被积函数变化剧烈，尤其是在场点和源点重合在一起的时候，被积函数是奇异函数，不能直接使用数值积分方法进行计算.必须要采用一些特殊方法来处理奇异点.

介质目标积分方程中包含L算子和K算子. 在本文中，只考虑L算子中的奇异点. 使用RWG基函数[6]进行离散，并使用伽略金法进行检验. 对于积分

(20)

有以下几种处理的方法：

方法1：提取法，从式(20)出发，对其中主值积分部分的G和G进行泰勒展开，对含有1/Rn项的积分通过极坐标变换进行处理[2,7-8]. 由于积分核中含有的G具有较高的奇异性，其计算精度可能会相对较差.

方法2：转移法，对式(20)使用矢量恒等式，将作用于格林函数G上的梯度算子转移到试函数上[2,6]，得到

降低了积分的奇异性. 理论上其计算精度应该比提取法高.

方法3：坐标变换法，使用等边参数空间变换，将奇异性分为共点、共线和共面3种情况分别处理，处理方法详见文献[3,9-10].

2.2 数值算例

以CTF为例，通过数值实验来研究和验证上述3种不同的L算子奇异点处理方法对矩量法计算精度的影响.下面实验中数据类型为双精度，迭代器为GMRES，迭代精度为10-8.

首先选择半径为0.5波长(λ)的球和边长为0.5λ的正8面体来验证算法. 入射波为沿-z方向入射，垂直极化的平面波，幅度为1.

分别计算了球和正8面体散射场的RMS. 图2中，分别给出了误差随不同网格剖分密度的变化情况. 其中网格剖分大小分别为λ/10，λ/20，λ/30和λ/40，球对应的未知数个数为972，4 332，10 092，18 252，正8面体对应的未知数个数为789，2 946，7 029，12 537. 从图中可以看到随着剖分逐渐变密，RMS值也逐渐减小，也即矩量法的误差逐渐减小. 同时，可以清楚地看到不同的奇异点处理方法下计算结果精度的差异. 方法1的误差明显大于另外两种方法，这与前面的分析相吻合. 而方法2和方法3则达到了类似的计算精度. 但是在计算稍复杂的正8面体时，方法3的精度略优于方法2.

为进一步验证本文提出方法的有效性和不同奇异点处理方式的精度，计算了几何构图如图3所示的圆柱腔. 入射波为沿-z方向入射的垂直极化平面波，幅度为1，频率为1.0 GHz. 图4给出了误差数据，未知数个数分别为3 039，6 705，16 998. 结果再次表明，方法1的精度差于方法2和方法3.

前面的算例中，使用入射等效源在外部不辐射的性质，验证了不同奇异点处理方式对于矩量法散射问题计算精度的影响，并得到了一些结论. 为进一步验证这些结论，计算了半径为0.5λ，相对介电常数ε为2.0的介质球散射场的雷达散射截面(RCS).和前面的算例相同，入射波为沿-z方向入射，垂直极化的平面波. 图5给出了以Mie级数解析解为参照的RCS均方根误差. 图中数据表明，方法2和方法3的精度优于方法1，即转移法和坐标变换法的精度优于提取法，与前面的结论相吻合.

3 结 论

对于任意形状目标，矩量法计算精度的验证非常重要. 根据等效原理，给出了一种具有明确参考基准，且适用于任意形状目标的精度验证方法. 使用这种方法对不同奇异点处理方法的精度进行了验证. 对球和正8面体等算例进行的数值实验，表明了所提出验证方法的有效性和通用性.

[1] Polimeridis A G，Vipiana F，Mosig J R，et al. DIRECTFN: fully numerical algorithms for high precision computation of singular integrals in galerkin sie methods[J]. IEEE Trans on Antennas Propagat，2013，61(6):3112-3122.

[2] 盛新庆.计算电磁学要论[M].2版.合肥:中国科学技术大学出版社，2008：23-24.

Sheng Xinqing. A brief treatise on computational electromagnetics[M]. 2nd ed. Hefei: Press of University of Science and Technology of China，2008:23-24. (in Chinese)

[3] Polimeridis A G，Yioltsus T V. On the direct evaluation of weakly singular integrals in galerkin mixed potential integral equation formulations[J]. IEEE Trans on Antennas Propagat，2008，56(9):3011-3019.

[4] Ergul Ö，Gurel L. Discretization error due to the identity operator in surface integral equations[J]. Computer Physics Communications，2009，180:1746-1752.

[5] Chew W C，Tong M S ，Hu B. Integral equation methods for electromagnetic and elastic waves[M]. [S.l.]: Morgan & Claypool，2009.

[6] Rao S M，Wilton D R，Glission A W. Electromagnetic scattering by surfaces of arbitrary shape[J]. IEEE Trans on Antennas Propagat，1982，30(3):409-418.

[7] Wilton D R ，Rao S M ，Glisson A W，et al. Potential integrals for uniform and linear source distributions on polygonal and polyhedral domains[J]. IEEE Trans. on Antennas Propag，1984，32(3):276-281.

[8] Graglia R D. On the numerical integration of the linear shape functions times the 3-D green’s function or its gradient on a plane triangle[J]. IEEE Trans on Antennas Propagat，1993，41(10):1448-1455.

[9] Polimeridis A G，Mosig J R. On the direct evaluation of surface integral equation impedance matrix elements involving point singularities[J]. IEEE Antennas and Wireless Propagation Letters，2011，10:599-602.

[10] Polimeridis A G，Tamayo J M，Rius J M，et al. Fast and accurate computation of hypersingular integrals in garlerkin surface integral equation formulations via the direct evaluation method[J]. IEEE Trans on Antennas Propagat，2011，59(6):2329.

(责任编辑：刘芳)

A New Method for Accuracy Analysis in Method of Moments

LIU Yan-nan, PAN Xiao-min, SHENG Xin-qing

(School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China)

A method to validate the accuracy of method of moments (MoM) for arbitrarily shaped targets was proposed. Based on equivalence principle，integral equations for dielectric objects were established. The non-radiating property of incident sources was derived by setting the medium on both sides of the interface the same. According to this property，the accuracy of MoM for arbitrarily shaped targets can be investigated. Numerical experiments were conducted on sphere and octahedron targets. It is validated that among three singularity treatments，nabla operator transfer and coordinate transformation perform better than extraction in terms of accuracy. The results also show that the proposed method is possessed of applicability and generality.

method of moments (MoM); accuracy; singularity

2014-03-06

国家教育部新世纪优秀人才支持计划(NCET-12-0045)；国家重点基础研究发展计划项目(2012CB720702)；国家自然科学基金资助项目(60901005，61371002)；北京市优秀人才培养资助项目(2012D0009011000002)

刘燕楠(1990—)，女，博士生，E-mail:ynliu1990@gmail.com.

潘小敏(1978—)，男，副研究员，E-mail:xman@bit.edu.cn.

O 441.4

A

1001-0645(2016)07-0723-04

10.15918/j.tbit1001-0645.2016.07.012