高考推理考点面面观

■山东省文登第一中学 崔 文

■山东省文登第一中学 侯宇虹



高考推理考点面面观

■山东省文登第一中学 崔 文

■山东省文登第一中学 侯宇虹

数学解题推理无处不在，演绎推理考查融于高考试卷大小题目之中，合情推理虽然不能用于数学证明，但可以发现数学规律，考查同学们的推理能力。

考点一：类比推理

类比推理是由特殊到特殊的推理，所得出的结论不一定正确。

解析：此题利用类比课本中推导等差数列前n项和公式的倒序相加法，尝试计算f(x)+f(1-x)为定值。

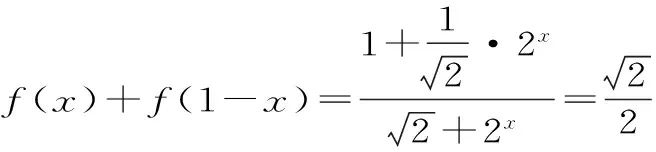
点评：高考中的类比一般包括概念之间的类比，形式之间的类比，性质之间的类比，数学方法之间的类比等。本例为数学思想方法类比。常见的命题载体有平面图形与立体图形，图形之间(如圆与椭圆)，等差数列与等比数列等。

考点二：合情推理与演绎推理综合运用

数学探索活动中，经常先用合情推理(归纳或类比)得出一个结论，然后用演绎推理进行证明，最终得出命题真假。

例2 (2013年福建卷)某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数。

(1)sin213°+cos217°-sin 13°cos 17°;

(2)sin215°+cos215°-sin 15°cos 15°；

(3)sin218°+cos212°-sin 18°cos 12°；

(4)sin2(-18°)+cos248°-sin(-18)°·cos 48°；

(5)sin2(-25°)+cos255°-sin(-25)°·cos 55°。

(Ⅰ)试从上述五个式子中选择一个，求出这个常数；

(Ⅱ)根据(Ⅰ)的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论。

sin2α+cos2(30°-α)-sinαcos(30°-α)

点评：“先推理，后证明”成为高考命题的一个方向。此类问题多与数学归纳法结合，先归纳得到一个结论，然后用数学归纳法进行证明。

(责任编辑 徐利杰)