聚焦《推理与证明》中的九类经典问题

■陕西省洋县中学 雍 康



聚焦《推理与证明》中的九类经典问题

■陕西省洋县中学 雍 康

推理与证明是在同学们已有知识的基础上完善了合情推理的两种方式——纳推理和类比推理，以及数学证明的主要方法——分析法、综合法、反证法等常用方法。上述推理方式和证明方法都是数学的基本思维过程，它们贯穿于整个高中数学的学习，能使同学们通过学习感受逻辑思维方式在数学以及日常生活中的作用。下面聚焦其经典问题，希望能有益于同学们的学习。

聚焦一：函数性质研究中的演绎推理

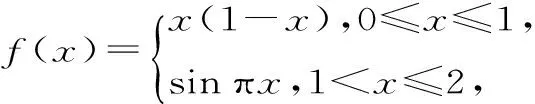
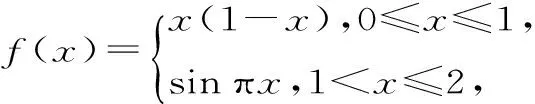
点评:已知周期函数在给定区间的解析式，可利用周期性和对称性将所求值化为在已知区间上求值。整个求解过程是从一般到特殊的推理过程，即演绎推理的过程，在大前提、小前提和推理形式都正确的前提下，得到的结论一定正确。

聚焦二：复合函数解析式中的归纳猜测

点评：归纳推理是由部分到整体，由特殊到一般的推理过程。在进行归纳时，通过取特殊值计算出几个结果，可以发现一般规律，从而做出合理的猜想，即合情推理。本题以复合函数解析式为载体,考查对递推关系的理解和应用,以及同学们的计算与归纳猜测能力。

聚焦三：“分裂数”中的归纳猜测

例3 (2015年山东淄博市高三模拟)对于大于等于1的自然数m的三次幂可用奇数进行以下方式的“分裂”：13=1，23=3+5，33=7+9+11，43=13+15+17+19，…。仿此，若m3的“分裂数”中有一个是2 015，则m____。

点评：解决这类问题时，首先观察式子的结构特点，其次观察式子中出现的字母之间的关系，再进行化简或运算。另外要注意对较为复杂的运算式，先不要化简，这样便于观察运算规律和结构上的共同点,有时还要借助等差或等比数列的性质简化求解。

聚焦四：等差与等比数列中的类比推理

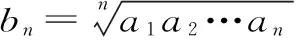
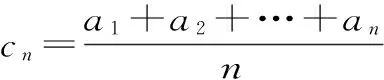
证明如下：设等差数列{an}的公差为d。

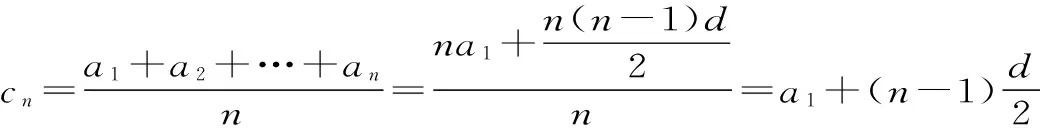
点评：把等差与等比数列进行类比，运用类比思想找出项与项的联系，应用等差、等比数列的性质是解决该题的关键。等差数列和等比数列有非常类似的运算和性质，一般情况下等差数列中的和(或差) 对应着等比数列中的积(或商)。

聚焦五：图形关系中的类比

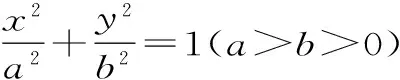
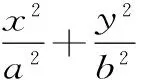
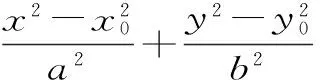
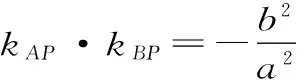
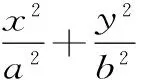
点评：图形关系中的类比，找两类对象的对应元素，找对应元素的对应关系，同时注意方法的类比。

聚焦六：数列推理中的综合法

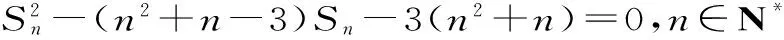
(1)求a1的值；

(2)求数列{an}的通项公式；

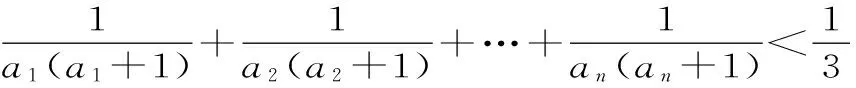
(Sn+3)[Sn-(n2+n)]=0。

因为an>0(n∈N*)，所以Sn>0。从而Sn+3>0，所以Sn=n2+n。

当n≥2时，an=Sn-Sn-1=n2+n-[(n-1)2+(n-1)]=2n。

又a1=2=2×1，所以an=2n(n∈N*)。

(3)对通项公式放缩变形重新改写，用裂项相消法求和，也可用观察法证明不等式。

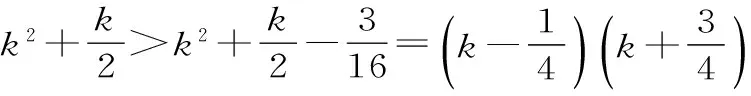
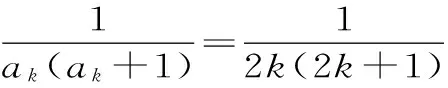
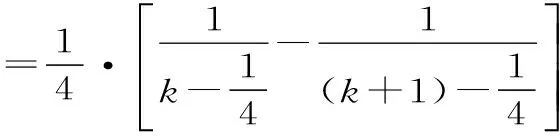
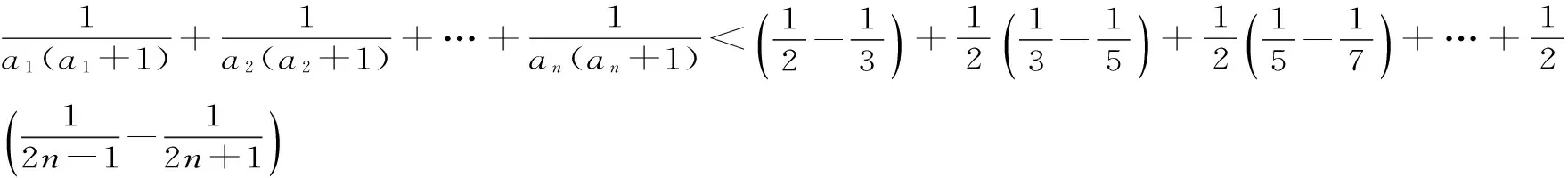
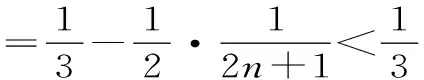
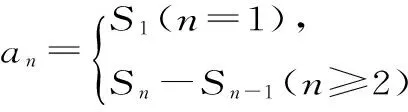
聚焦七：不等式证明中的综合分析

例7 设a,b,c均为大于1的正数，且ab=10。

求证：logac+logbc≥4lgc。

证明：单一运用综合法或分析法很复杂，本题若两者均用，效果更好。

a>1,b>1,故lga>0,lgb>0。

故原不等式得证。

点评：分析法与综合法各有优势，证明问题时，可结合使用，先以分析法为主寻求解题思路，再用综合法有条理地解答或证明。两者交替使用，较易成功。这种方法不仅在证明不等式时经常用到，在解决其他数学问题时也常常用到。

聚焦八：新定义问题中的合情推理

A．77 B．49 C．45 D．30

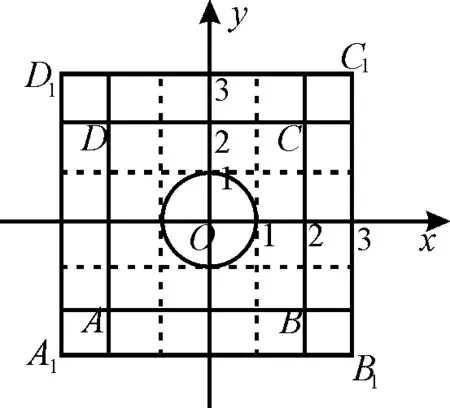
图1

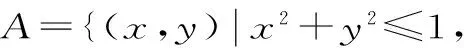
点评：这是一道与集合相关知识的新定义题型。通过给出一个新定义，或约定一种新运算，或给出几个新模型来创设全新的问题情景，要求同学们在阅读理解的基础上，依据题目提供的信息，联系所学的知识和方法，结合图形实现信息的迁移，达到灵活解题的目的。

聚焦九：先猜后证中的数学归纳法

(1)当n=1,2,3时，试比较f(n)与g(n)的大小关系；

(2)猜想f(n)与g(n)的大小关系，并给出证明。

解析：由特殊到一般，先猜再用数学归纳法证明。

(1)当n=1时，f(1)=1，g(1)=1，所以f(1)=g(1)。

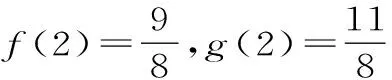
(2)由(1)猜想f(n)≤g(n)，下面用数学归纳法给出证明。

①当n=1,2,3时，不等式显然成立。

②假设当n=k(k≥3，k∈N*)时不等式恒成立，即：

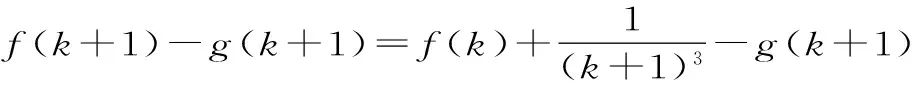
所以f(k+1)

由①、②可知，对一切n∈N*，都有f(n)≤g(n)成立。

(责任编辑 徐利杰)