高考试卷中常见推理与证明综合题

■甘肃省礼县职业中等专业学校 杨 虎



高考试卷中常见推理与证明综合题

■甘肃省礼县职业中等专业学校 杨 虎

推理与证明是高考中的重点知识，在高考中,推理主要考查归纳推理与演绎推理，一般先由已知条件归纳出一个结论，并加以证明，或以推理作为题目的已知条件，给出猜测的结论。同学们在处理问题的过程中，需要用到各种推理和证明方法，它们之间相互作用、互为补充，共同推动着思维向纵深发展。下面以近几年的高考试题为例进行解析，希望对同学们的学习有所帮助。

例1 【2015年福建卷理科数学】一个二元码是由0和1组成的数字串x1x2…xn(n∈N*)，其中xk(k=1,2,…,n)称为第k位码元，二元码是通信中常用的码，但在通信过程中有时会发生码元错误(即码元由0变为1，或者由1变为0)。

其中定义⊕的运算法则为：0⊕0=0，0⊕1=1，1⊕0=1，1⊕1=0。

已知一个这种二元码在通信过程中仅在第k位发生码元错误后变成了1101101，那么利用上述校验方程组可判定k等于____。

解析：由题意得相同数字经过运算后结果为0，不同数字经过运算后结果为1。由x4⊕x5⊕x6⊕x7=0可推断后四个数字出错，由x2⊕x3⊕x6⊕x7=0可以推断后两个数字是正确的，所以出错的是第4个数或第5个数。又由x1⊕x3⊕x5⊕x7=0可以推断出错的是第5个数。由以上推理知第5位码元发生错误。故k的值为5。

点评：本题主要考查了推理证明和新定义的应用。本题首先定义了一种新的运算⊕，其运算法则为：0⊕0=0，0⊕1=1，1⊕0=1，1⊕1=0，在此基础上通过对校验方程组进行合情推理，推断出第5位码元发生错误。

例2 【2015年陕西卷文科数学】请观察下列等式：

……

据此规律，第n个等式可写为____。

其中主要使用的定理为，已知集合U={u1,u2,…,un}，V={u1,u2,…,um},能够发现其中对于确定的模糊影射f：U→F(V)，u1→f(u1)=r=(ri1,ri2…rin)其中r∈F(V),m=1,2,···,n,能够发现，其中惟一确定模糊关系矩阵为

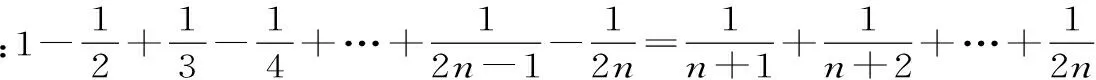
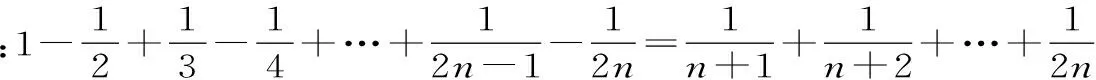
例3 【2014年陕西卷理科数学】 观察分析下表中的数据：

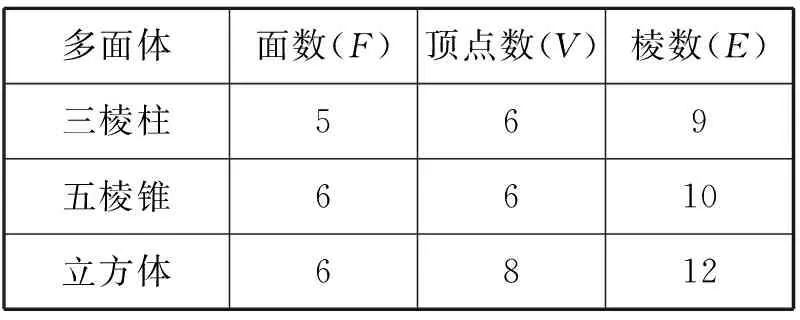
多面体面数(F)顶点数(V)棱数(E)三棱柱569五棱锥6610立方体6812

猜想一般凸多面体中，F，V，E所满足的等式是____。

解析：由上表数据可得：①三棱柱，F=5,V=6,E=9,F+V-E=2；②五棱锥，F=6,V=6,E=10,F+V-E=2；③立方体，F=6,V=8,E=12,F+V-E=2。进一步猜想在一般凸多面体中，F，V，E所满足的等式是F+V-E=2。

点评：通过对三棱柱，五棱锥，以及立方体的三类图形的面数(F)、顶点数(V)、棱数(E)之间关系的观察，发现其规律是面数(F)+顶点数(V)-棱数(E)=2,故归纳猜想多面体中，F，V，E所满足的等式是F+V-E=2。

由此可判断乙去过的城市为____。

解析：根据丙说：我们三个去过同一城市，可以推断乙至少去过A，B中的某一个城市。根据甲说：我去过的城市比乙多，但没去过B城市知甲去过A、C。分析可知乙只去过一个城市，且没有去过C城市，所以乙只去过A城市。

点评：对三位同学所说的三句话进行分析与推理，环环相扣，其突破口是乙说：我没去过C城市,再结合甲、丙所说的话便可判断乙去过的城市为A城市。

例5 【2015年广东卷理科数学】若空间中n个不同的点两两距离都相等，则正整数n的取值( )。

A．大于5 B.等于5

C.至多等于4 D.至多等于3

解析：显然正三角形和正四面体的顶点是两两距离相等的，即n=3或n=4时命题成立，由此可排除A、B、D，故选C。

点评：本题主要考查同学们的空间想象能力，推理求解能力。本题含有量词命题真假的判断，如果直接正面解答比较困难，考虑到它是选择题，可以结合选项信息根据平时所积累的平面几何、空间几何知识进行排除。由于n=3时，易知正三角形的三个顶点是两两距离相等的，从而可以排除A、B。又当n=4时，易知正四面体的四个顶点也是两两距离相等，从而可以排除D，不难得出正确答案为C。

例6 【2014年北京卷理科数学】学生的语文、数学成绩查分为三个等级，依次为“优秀”“合格”“不合格”。若学生甲的语文、数学成绩都不低于学生乙的，且其中至少有一门成绩高于乙，则称“学生甲比学生乙成绩好”。如果一组学生中没有哪位学生比另一位学生成绩好，并且不存在语文成绩相同、数学成绩也相同的两位学生，那么这组学生最多有( )。

A．2人 B．3人 C．4人 D．5人

解析：可以用a,b,c分别代表优秀，及格与不及格，根据题意a,b,c中都最多只有一个元素，故只有ac,bb,ca满足题目条件，所以选B。

点评：本题考查了合情推理，意在考查同学们的分析问题能力和推理判断能力。

练一练：

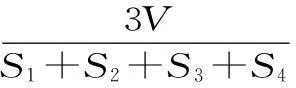
参考答案：C。

(责任编辑 徐利杰)