环Z4+uZ4+u2Z4上的循环码

王艳萍,刘 丽

(合肥工业大学 数学学院，安徽 合肥 230009)



环Z4+uZ4+u2Z4上的循环码

王艳萍,刘 丽

(合肥工业大学 数学学院，安徽 合肥 230009)

循环码;环同态;Gray映射;准循环码

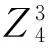
1 环R=Z4+uZ4+u2Z4

设环R=Z4+uZ4+u2Z4(u3=0),则R是一个特征为4的交换环,且其同构如下：

环R中元素z有如下形式:z=a+ub+u2d,其中a,b,d∈Z4;环R的单位为{±1+iu+ju2|i,j∈Z4},环R的非单位为{l+mu+nu2|l=0,2;m,n∈Z4}。显然环R的所有理想中,I2,u={i+ju+ku2|i=0,2;j,k∈Z4}是Z4+uZ4+u2Z4中唯一包含所有非单位的理想,因此I2,u是环R唯一极大理想且非主理想。

本文将环R的单位分成ο1和o2两组,即

则对∀b∈R,有

2 商环Rn及其性质

2.1 定义

设Q为有限环,Qn是分量属于Q的n元数组，环Q上长为n的线性码是Qn的Q-子模，Q[x]是系数属于Q的多项式环，商环Qn=Q[x]/〈xn-1〉。

定义1 对于任意的环Q,若N满足N(c0,c1,…,cn-1)=(cn-1,c0,…,cn-2),其中,ci∈Q,i=1,2,…,n,则称N是Q上的一个循环移位。

定义2 设C是环Q上长为n的线性码,若对∀(c0,c1,…,cn-1)∈C,都有N(c0,c1,…,cn-1)=(cn-1,c0,…,cn-2)∈C,则称C是Q上长为n的循环码。

定义映射:

则映射η是一一映射。容易验证。

引理1 环Q上长为n的线性码C是循环码，当且仅当η(C)是Q[x]/〈xn-1〉的理想。

2.2 环Rn的性质

为了研究环R上循环码的结构,首先要研究商环Rn=(Z4+uZ4+u2Z4)[x]/〈xn-1〉的结构。

引理2 环Rn不是主理想环。

证明 由文献[11]知,对任意有限环Q,Q[x]/〈xn-1〉≅QM,QM是群环,M是一个n阶循环群M=〈m:mn=1〉。定义满同态如下:

μ:QM→Q,

μ(u0+u1m+…+un-1mn-1)=u0+u1+…+un-1。

因此,可以定义同态映射如下:

显然映射μ为满同态。又因为环R的理想I=〈2,u〉不是主理想,可以令K=μ-1(I),显然K是Rn的一个理想。又因为μ是满射,所以μ(K)=μ(μ-1(I))=I。若K是主理想,则μ(K)=I也是主理想,这与I不是主理想矛盾。所以K不是主理想,从而环Rn不是主理想环。

命题1 当n=2ks(s为大于1的奇数)时,环Rn是非局部环。

证明 由文献[12]知,一个环是局部环，当且仅当环的所有非单位构成它的唯一极大理想。当n=2ks(s是大于1的奇数)时,在Rn中,有

令h1(x)=x2k(s-1)+x2k(s-2)+…+1,则h1(x)是Rn的非单位。

又因为s是大于1的奇数,所以

令h2(x)=x2k(s-2)+x2k(s-3)+…+1。因为μ是环同态映射,所以h2(x)是非单位。因为

所以μ(h1(x)+h2(x))=1+2(s-1)=1,从而h1(x)+h2(x)是Rn的单位,即在Rn中,非单位与非单位的和为单位。由此推出Rn的所有非单位不能构成Rn的一个理想,结论成立。

命题2 若环Rn中的元素a不是0也不是单位,则a是Rn的零因子。

证明 设0≠a∈Rn是一个非单位,则

从而

于是存在b1,b2∈Rn,b1≠b2,使得：

b1a=b2a,

即

由此可得a是Rn的零因子。

定理1 若n=2k(k≥2),则环Rn是局部环。

证明 一个环是局部环当且仅当该环的所有非单位构成它的唯一极大理想。而在R2k中非单位乘以其任意一个元素都不可能是单位,因此只需证R2k的所有非单位构成其一个加法子群。在环Rn中,若λ是环R的非单位,则δ+λf(x)是Rn中的单位(其中δ∈R)当且仅当δ是环R中的单位。

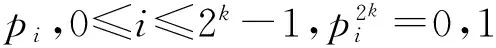
若Δ={1,3,1+2u2,3+2u2}，则Δ可以表示成Δ=1+2z的形式。

若Δ={0,2,2+2u2}，则Δ可以表示成Δ=2z的形式,其中z∈R。

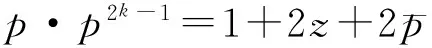
因此,元素p=p0+p1x+…+p2k-1x2k-1是一个非单位当且仅当存在偶数个pi是单位,也就是有偶数个pi是非单位。又因为在环R中,非单位与非单位的和为非单位,单位与单位的和为非单位,单位与非单位的和为单位。由此推出所有包含偶数个pi是单位的元素p构成了R2k的一个加法子群。证毕。

2.3 Rn中单位和非单位的特点

用循环矩阵来表示RM，即:

由文献[13]知,对于任意的ε∈Rn是单位当且仅当det(δ(ε))在环R中是单位,其中det表示循环矩阵行列式。

命题3ε=c0+c1x+…+cn-1xn-1是Rn中的单位当且仅当det(δ(ε))在R上是单位;ε∈Rn是非单位当且仅当det(δ(ε))∈I2,u。

例如,当n=4时,

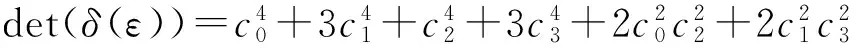
ε在R4中是单位当且仅当det(δ(ε))在环R上是单位;ε在R4中是非单位当且仅当det(δ(ε))∈I2,u。

3 环R上循环码结构

记

S=Z4+uZ4,

R=Z4+uZ4+u2Z4,

为了寻求R4上循环码的生成元,需要求出Sn上循环码的生成结构。首先,给出Z4[x]/〈xn-1〉的结构。

引理3 设D为Z4[x]/〈xn-1〉中的循环码[14],则有：

(1) 若n为奇数,则Z4[x]/〈xn-1〉为一个主理想环,D=〈g(x),2a(x)〉=〈g(x)+2a〉,其中,g(x),a(x)∈Z2[x]/〈xn-1〉,且a(x)|g(x)|(xn-1)mod 2。

(2) 若n为偶数,且g(x)=a(x),则D=〈g(x)+2p(x)〉,其中，g(x),p(x)∈Z2[x]/〈xn-1〉,且g(x)|(xn-1)mod 2,g(x)|p(x)((xn-1)/g(x))；g(x)≠a(x),则D=〈g(x)+2p(x),2a(x)〉,其中,g(x),a(x),p(x)∈Z2[x]/〈xn-1〉,且a(x)|g(x)|(xn-2)mod 2,a(x)|p(x)((xn-1)/g(x))，degg(x)> dega(x)>degp(x)。

定义映射φ1:R→S,使得φ1(a+ub+u2d)=a+ub,易证φ1是同态映射,且kerφ1=u2Z4。此映射可扩展为多项式环上的一个同态映射Ψ1:

设C是R上长为n的循环码,则C是Rn的理想。将Ψ1限制在C上,则Ψ1(C)在循环移位下也是不变的，因此C在Ψ1下的像Im (Ψ1)为S上的循环码,而ker (Ψ1)是u2Z4上的循环码。

同样定义映射φ2:S→Z4,使得φ2(a+ub)=a。易证φ2是同态映射,kerφ2=uZ4,扩展映射如下:

设F是S上的循环码,则F是Sn的理想。将Ψ2限制在F上,则Ψ2(F)在循环移位下也是不变的，因此F在Ψ2下的像Im(Ψ2)是Z4上长为n的循环码,而ker(Ψ2)是u2Z4上的循环码。

定理2 设F是Sn上的循环码,则

(1) 若n为奇数,则有：

ug2(x)+2ua2(x)〉,

其中gi(x),ai(x)∈Z2[x]/〈xn-1〉,ai(x)|gi(x)|(xn-1)mod 2,i=1,2,b(x)∈Z4[x]/〈xn-1〉。

(2) 若n为偶数,则有：

2a1(x)+ub2(x),

ug2(x)+2up2(x),2ua2(x)〉,

其中,gi(x),ai(x),pi(x)∈Z2[x]/〈xn-1〉,bi(x)∈Z4[x]/〈xn-1〉,满足：

若gi(x)=ai(x),则有：

ug2(x)+2up2(x)〉,

其中,gi(x)|pi(x)((xn-1)/gi(x)),i=1,2；b3(x)∈Z4[x]/〈xn-1〉。

证明 (1) 若n为奇数,则Z4[x]/〈xn-1〉中的理想D′=〈g(x),2a(x)〉=〈g(x)+2a(x)〉。

因为Im(Ψ2)是Z4上的循环码,所以

其中,a1(x)|g1(x)|(xn-1)mod 2。又因为ker(Ψ2)是uZ4上的循环码,所以

其中,a2(x)|g2(x)|(xn-1)mod 2。结论成立。

(2) 若n为偶数,则Z4[x]/〈xn-1〉中的理想D″=〈g(x)+2p(x),2a(x)〉。

因为Im(Ψ2)是Z4上的循环码,所以

又因为ker(Ψ2)是uZ4上的循环码,所以

其中,gi(x)、ai(x)、pi(x)∈Z2[x]/〈xn-1〉,且满足ai(x)|pi(x)((xn-1)/gi(x)),ai(x)|gi(x)|(xn-1)mod 2。结论成立。

定理3 设C为Rn中的循环码,

(1) 若n为奇数,则有：

ug2(x)+2ua2(x)+u2d2(x),

u2g3(x)+2u2a3(x)〉，

其中，gi(x),ai(x)∈Z2[x]/〈xn-1〉,ai(x)|gi(x)|(xn-1)mod 2,i=1,2,3，b1(x),d1(x),d2(x)∈Z4[x]/〈xn-1〉。

(2) 若n是偶数,则

2a1(x)+ub2(x)+u2r2(x),

ug2(x)+2up2(x)+u2r3(x),

2ua2(x)+u2r4(x),

其中,gi(x),ai(x),pi(x)∈Z2[x]/〈xn-1〉,i=1,2,3；bj(x),rk(x)∈Z4[x]/〈xn-1〉,j=1,2;k=1,2,3,4,满足ai(x)|pi(x)((xn-1)/gi(x)),ai(x)|gi(x)|(xn-1)mod 2。

若gi(x)=ai(x),则有：

ug2(x)+2up2(x)+u2r6(x),

其中,gi(x)|pi(x)((xn-1)/gi(x));b3(x),rk(x)∈Z4[x]/〈xn-1〉,k=5,6。

证明 (1) 若n为奇数,则环Sn中的理想F′=〈g1(x)+2a1(x)+ub1(x),ug2(x)+2ua2(x)〉。

因为Im(Ψ1)是环S上的循环码,所以Im(Ψ1)=〈g1(x)+2a1(x)+ub1(x),ug2(x)+2ua2(x)〉。又因为ker(Ψ1)是u2Z4上的循环码,所以有：

其中,ai(x)|gi(x)|(xn-1)mod 2,i=1,2,3,4。

综上可得环Rn上的长为n的循环码为:

ug2(x)+2ua2(x)+u2d2(x),

u2g3(x)+2u2a3(x)〉。

(2) 若n为偶数,证明方法同上。

例 当n=7时,x7-1=(x+1)(x3+x+1)(x3+x2+1)mod 2。取

则环Sn上的循环码如下:

环Rn上的循环码如下:

2u(x3+x+1)+u2(2x+3),u2(x3+

4 环R上循环码的Gray像

定义3 设C是环R上长度为n=ml的线性码，若对任意(c0,c1,…,cn-1)∈C,有

其中,下角标作模n运算,则C称为R上的l-准循环码。

定义映射:

其中,a、b、d∈Z4。

显然映射ξ为双射。映射ξ可扩展为:

定义4 定义R上的Lee重量wL为:

wL(a+ub+u2b)=wL(d,d+b,a+b+d),

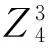
环Rn中码字的Lee重量为其码元的Lee重量之和,2个码字c、c′的Lee距离为c-c′的Lee重量,因此可得以下定理。

引理4 设N是一个循环移位,则

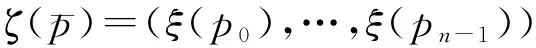
综上可得ξ∘N=N3∘ζ。

定理5 若P是R上长为n的线性码且码字个数为K,则ξ(P)是Z4上长为3n的线性码且码字个数也为K。

证明 由定理4可知ζ是保距映射。由ζ的定义知,ζ(P)的长度为3n。令

对于0≤i≤n-1,有

于是

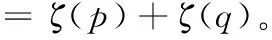
若α∈Z4,p∈R,则有：

由上可知,ζ保持线性运算。又因为ζ是双射,所以P和ζ(P)有相同的码字。

定理6 若P是R上长为n的循环码,则ζ(P)是Z4上长为3n的3-准循环码。

证明 设P是R上的循环码,则N(P)=P。由引理4得:

结论成立。

5 结 论

本文主要对环Z4+uZ4+u2Z4上任意长度的循环码进行了研究,得到了循环码的结构,并研究了环Z4+uZ4+u2Z4上循环码的一个Gray像。对于有限非链环上循环码理论的研究,本文具有一定的推广价值及借鉴意义。环Z4+uZ4+u2Z4上常循环码或负循环码的结构与性质,将是进一步研究的方向。

[1] HAMMONS A R,KUMAR P V,CALDERBANK A R,et al.TheZ4-linearity of Kerdock,Preparata,Goethals,and related codes[J].IEEE Trans Inform Theory,1994,40(2):301-319.[2] WOLFMAN N J.Negacyclic and cyclic codes overZ4[J].IEEE Trans.Inform.Theory,1999,45(7):2527-2532.

[3] PLESS V,SOLE P,QIAN Z.Cyclic self-dualZ4-codes[J].IEEE International Symposium on Intromation Tehory,1997,3(1):48-69.

[4] BLACKFORD T.Cyclic codes overZ4of oddly even length[J].Discr Appl Math,2003,128(1):27-46.

[5] BONNECAZE A,UDAYA P.Cyclic codes and self-dual codes overF2+uF2[J].IEEE Trans Inform Theory,1999,45(4):1250-1255.

[6] QIAN J F,ZHANG L N,ZHU S X.Cyclic code overFp+uFp+…+uk-1Fp[J].IEICE Transactions on Fundamentals of Electronics,Communications and Computer,2005,E88-A(3):795-797.

[7] ABUALRUB T,SIAP I.Cyclic codes over the ringsZ2+uZ2andZ2+uZ2+u2Z2[J].Designs, Codes and Cryptography,2007,42(3):273-287.

[8] 王立启,朱士信.环F2[u]/(u4)上的一类常循环码及其Gray像[J].电子与信息学报,2013,35(2):499-503.

[9] YILDIZ B.KARADENIZ S.Cyclic codes overF2+uF2+vF2+uvF2[J].Des Codes Cryptogr,2011,58(3):221-234.

[10] YILDIZ B.KARADENIZ S.Linear codes overF2+uF2+vF2+uvF2[J].Des Codes Cryptogr,2010,54(1):61-81.

[11] ABUALRUB T.Cyclic codes over the ring of integers modm[D].Lowa:University of Lowa,1998.

[12] HUNGERFORD T W.Algebra[M].New York:Springer,1974:389-428.

[13] HURLEY T.Group rings and rings of matrices[J].Inter J Pure Appl Math,2006,31(3):319-335.

[14] ABUALRUB T.Reversible quaternary cyclic codes[C]//Proceedings of the 9th WSEAS International Conference on Applied Mathematics Istanbul,Turkey,May 27-29,2006:441-446.

(责任编辑 朱晓临)

Cyclic codes over the ringZ4+uZ4+u2Z4

WANG Yanping,LIU Li

(School of Mathematics, Hefei University of Technology, Hefei 230009, China)

cyclic code; ring homomorphism; Gray map; quasi-cyclic code

2015-04-15

国家自然科学基金资助项目(11201107；11401154)

王艳萍(1989-),女,安徽太和人,合肥工业大学硕士生;

刘 丽(1965-),女,安徽枞阳人,博士,合肥工业大学教授,硕士生导师.

10.3969/j.issn.1003-5060.2016.10.027

TN911.22

A

1003-5060(2016)10-1432-06