微分博弈下政府税收与企业再投资的互动策略研究

徐 晟,夏宝藏,唐庭正

(合肥工业大学 管理学院,安徽 合肥 230009)



微分博弈下政府税收与企业再投资的互动策略研究

徐 晟,夏宝藏,唐庭正

(合肥工业大学 管理学院,安徽 合肥 230009)

文章以Solow增长模型中的新古典生产函数为基础,结合随机微分理论和动态博弈理论,将政府税率和企业再投资率设为内生变量,构建了政府-企业博弈系统,分析了政府税收和企业再投资最优策略,并通过数值方法分析了现实经济问题。

随机过程;微分博弈;政府税收;再投资率

0 引 言

市场在资源配置中的决定性作用有利于最大限度地激发市场主体企业的创新活力,更好发挥政府作用有利于建设高效的服务型政府,从而加快我国经济转型升级，构建开放型经济新体制。本文从企业和政府角度出发,探讨政府税收行为和企业再投资行为间的博弈问题,以期在获得经济持续增长的同时,推动社会财富得到公平分配。

本文以Solow增长模型中的新古典生产函数、随机微分理论和动态博弈理论为基础展开研究[1-2]。文献[3-4]讨论了人力资本和物质资本在生产部门以及在经济增长中的最优配置问题,但是均没有考虑到创造力对经济增长的贡献。文献[5-6]将创造力以及人力资本作为参数引入模型以解决经济增长问题,进而建立了一个内生经济增长模型,但是在寻求内生经济增长模型均衡解时没有考虑到厂商和员工间的博弈问题。文献[7]建立了一种基于微分博弈理论的经济增长模型,但没有考虑现实世界中的不确定性。鉴于此，本文构建了政府-企业博弈系统,并将政府税率和企业再投资率设为内生变量,据此分析政府税收和企业再投资最优策略,并通过数值方法分析了现实经济问题[8-13]。

1 模型与假设

根据Solow理论原理,生产函数可表示为:

(1)

其中,t为时间;Y为产出;K为资本;A为技术的水平;L为劳动力。

设F为生产函数的固定回报,同时令k(t)=K/AL为每单位有效劳动的资本量。因此,可将单位有效劳动的产出写成单位有效劳动的函数，具体公式如下:

(2)

政府目标:

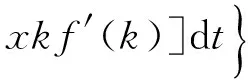
(3)

企业目标:

(4)

资本积累的动态系统可表示为:

(5)

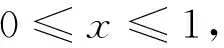
其中，k为单位有效劳动资本;x为税率;s为被企业控制的再投资率。

2 博弈均衡及数值分析

2.1 政府和企业最优策略

政府-企业微分博弈构成了一个开环的纳什均衡。开环微分博弈的纳什均衡解决方案应该是一个策略集,包含政府最优策略-最优税率和企业最优策略-最优再投资率,具体可表示为{x*(k),s*(k)},从而得到政府和企业的最优策略集分别为:

政府策略:

(6)

企业策略:

(7)

其中，a=s(x-1)[f′(k)+kf″(k)]-c；

bG=-xf′(k)+(1-x)kf″(k)；

bF=(s-1)(1-x)[f′(k)+kf″(k)]；

其中,n为人口的增长率;g为技术的增长率;δ为资本-有效劳动力的自然衰减率;c=n+g+δ>0。

证明 这个模型是无限期贴现的优化问题,策略集{x*(k),s*(k)}应满足哈密顿方程。政府和企业的哈密顿方程HG和HF分别为:

(8)

(9)

将(5)式代入(8)式和(9)式可得:

(10)

(11)

因为这是一个bang-bang问题,所以政府哈密顿方程HG和企业哈密顿方程HF的最大值在政府的控制变量x和企业的控制变量s满足以下条件时得到:

(12)

(13)

为了得到这个模型的开环纳什均衡解,还应该满足(5)式及以下偏微分方程组:

(14)

(15)

政府与企业的哈密顿函数的共态参数方程可表示为以下动态形式:

(16)

(17)

解上述常微分方程可得:

(18)

(19)

其中，NG和NF为待定系数,将终止条件代入(18)式和(19)式可得Ni=0，i=G,F。由此可知，政府与企业的共态参数可以表示为:

(20)

(21)

据此可以得到政府与企业的最优策略集。

2.2 最优策略的经济解释

当λF>e-ρ t时,企业的策略s*=1,即企业将所有的投资利润投入到再生产过程中。在这种情况下政府的策略包含2种情况:

(1) 当λG>e-ρ t/s时,政府选择策略是x*=0。这种策略表现为:政府将不会对企业征收任何的税款,同时企业选择将所有的投资利润投入到再生产过程中,即策略集为{0,1}。

(2) 当λG

莫莉是个小资女人，有给首长看病的大夫爸爸，有留洋的官二代男友，仿佛什么都有了。唯独没有归属感。赶上三连连长，愣头青的沐建峰，干柴猛火，挡不住。其后，沐建峰和赵益勤爱情、娶亲，莫莉也在他的生存中来往自若。

当λF

(1) 当λG>e-ρ t/s时,政府选择的策略是x*=0。这种策略表现为:政府将不会对企业征收任何的税款,同时企业没有将任何的投资增值投入到再生产过程中,即策略集为{0,0}。从逻辑上分析,这种策略既没有保证经济长期的增长,也没有获得公平的二次分配,因此这种策略{0,0}是不稳定的。

(2) 当λG

综上所述,政府与企业的均衡只会出现2种策略集,即{0,1}和{1,0}。

2.3 数值分析

政府与企业的策略集分4种情况,假设各参数取值分别为:a=0.9,ρ=0.08,k0=100,c=0.03。由于数值分析不能取到无穷时间点,本文将时间终止点选在T=100处。程序中具体表示见表1所列,数值分析结果如图1所示。

表1 政府-企业策略集符号

图1 确定条件下政府-企业策略及资本积累

由图1可知,若政府与企业在博弈的开始阶段就选择了{1,0}策略,则经济出现了持续的负增长,显然这种选择对经济增长是不利的。

3 模型改进

为了使经济得到不断增长,必须保证企业获得足够收益，那么政府最大税率必然不会选择为1,同时为了保证社会公平得到体现,政府的最小税率也必然不会为0。因此,本文将模型中政府税率的区间修改为[xmin,xmax],其中0

3.1 模型设立

政府目标:

(22)

企业目标:

(23)

0≤s≤1,

k(0)=k0。

解(14)式、(15)式微分方程可得:

(24)

(25)

由此可以得到政府与企业的最优策略集,具体表达式如下。

政府策略:

(26)

企业策略为:

(27)

3.2 数值分析

假设参数取值分别为:a=0.7，ρ=0.08，k0=100，c=0.06，xmin=0.1，xmax=0.5，博弈终止时间T=60。若在某种情况下,政府与企业的策略具有多种选项,假设各种被选的策略概率相同。

程序中具体表达仍见表1所列,通过数值模拟可得政府与企业的策略以及资本的积累关系如图2所示。

由图2可知,t的范围在[0,31]左右的阶段,政府与企业采用的是混合策略即{0.1,1}和{0.5,1},经济处于起步阶段。无论政府采用最大税率政策还是最小税率政策,企业采取的策略都是将投资收益投入到再生产过程中,从而推动经济的发展。

当t达到31左右时,政府与企业都采用单一的策略{0.1,1},属于经济腾飞阶段。政府采取低税率政策,企业将所有的资本积累投入到再生产活动中,从而推动经济的高速发展。但是,这一阶段社会贫富差距也在加大,这一过程大概持续8a左右。

当t达到39左右时,经济发展达到了顶峰。在t∈[39,48]时,政府与企业都采用了混合策略{0.1,1}和{0.5,0},经济出现了缓慢下滑。当政府税率低时,企业还可能将收入用于投资,但是当政府的税率过高时,企业选择了消费。本文假设这2种情况概率相当,因此经济虽然出现了下滑,但是部分企业的投资保证了经济下滑不那么明显。

图2 政府-企业策略及资本积累

在最后的12 a时间里,政府与企业的策略为单一的{0.5,0},企业选择将所有的财富用于消费,而政府显然既不会不顾及经济的增长,又不顾社会的公平,因此这个阶段经济出现持续衰退。

4 结 论

本文通过构建政府与企业的动态博弈模型,运用开环纳什均衡解法求解政府-企业最优策略集。为了使模型更加符合经济现实,本文对模型进行了改进,并使用数值分析方法较好地模拟了经济发展现实。本文研究结果表明,在经济发展的不同阶段,政府与企业应采用混合或单一的互动策略,充分发挥市场主导、政府服务作用,以保证经济持续增长,实现资源优化配置。未来的研究可以从以下方面进行扩展:考虑到政府与企业在博弈系统中并不是平等的博弈参与者,政府作为领导者,企业作为追随者,可以采用反馈斯坦伯格均衡解法。

[1] SOLOW R M.A contribution to the theory of economic growth[J].Quarterly Journal of Economics,1956,70(1):65-94.

[2] SOLOW R M.Technical change and the aggregate production function[J].Review of Economics and Statistics,1957,39(3):312-320.

[3] LUCAS R E, J K.On the mechanics of economic development[J].Journal of Monetary Economics,1988,22:3-42.

[4] UZAWA H.Optimal growth in a two-sector model of capital accumulation[J].Review of Economic Studies,1964,31(1):1-24.

[5] ROMER P M.Endogenous technological change[J].Journal of Political Economy,1990,98(5):71-102.

[6] ROMER P M.Increasing returns and long-run growth[J].Journal of Political Economy,1986,94(5):1002-1037.

[7] LANCASTER K.The dynamic inefficiency of capitalism[J].Journal of Political Economy,1973,81(5):1092-1109.

[8] 杨友才.引入制度因素的经济增长模型与实证研究[D].济南:山东大学,2009.

[9] 周少波.随机优化方法在资源配置模型中的应用[D].武汉:华中科技大学,2006.

[10] 赵辉.资本积累、技术进步与劳动力市场动态:马克思经济增长理论与模型研究[D].天津:南开大学,2009.

[11] 柴洪辉.从马尔萨斯陷阱到平衡增长:统一增长模型[D].上海:上海交通大学,2009.

[12] 徐晟,徐媛,赵惠芳.负二项分布在区域自主创新评价中的应用[J].合肥工业大学学报(自然科学版),2010,33(1):138-142.

[13] 赵惠芳,杨苏,徐晟.专利最优保护期限的经济学分析[J].合肥工业大学学报(自然科学版),2008,31(7):1037-1041.

(责任编辑 万伦来)

Interaction between government tax and enterprise reinvestment based on differential game theory

XU Sheng,XIA Baocang,TANG Tingzheng

(School of Management, Hefei University of Technology, Hefei 230009, China)

Based on the new classical production function of Solow growth model, the stochastic differential theory and the dynamic game theory, the game system between the government and enterprises is built, in which the government tax rate and the enterprise reinvestment rate are set as endogenous variable. The optimal strategies of the government tax and the enterprise reinvestment are analyzed, and the economic reality is studied by using the numerical model.

random process; differential game; government tax; reinvestment rate

2015-04-10；

2015-06-12

徐 晟(1972-) ,男,湖北浠水人,博士,合肥工业大学副教授,硕士生导师.

10.3969/j.issn.1003-5060.2016.10.024

F275

A

1003-5060(2016)10-1416-00