改进的朴素贝叶斯增量算法研究
2016-11-24曾谁飞张笑燕杜晓峰陆天波
曾谁飞,张笑燕,杜晓峰,陆天波
(1. 北京邮电大学软件学院,北京 100876;2. 北京邮电大学计算机学院,北京 100876)
改进的朴素贝叶斯增量算法研究
曾谁飞1,张笑燕1,杜晓峰2,陆天波1
(1. 北京邮电大学软件学院,北京 100876;2. 北京邮电大学计算机学院,北京 100876)
提出了一种新增特征的朴素贝叶斯增量算法。在无标注语料增量样本的选择上,借助传统的类置信度阈值,构建一个最小后验概率作为样本选择的双阈值,当识别到增量语料中有新的特征时,会将该特征加入到特征空间,并对分类器进行相应的更新,发现对类置信度阈值起到很好的补充作用,最后利用了无标注和有标注语料验证所提算法。实验结果表明,改进的朴素贝叶斯增量算法较传统增量算法表现出了更优的增量学习效果。
朴素贝叶斯;增量算法;特征空间;评价指标
1 引言
伴随人工智能技术的快速发展,市场对智能机器人的热度持续升温,谷歌阿尔法狗大战、苹果Siri、IBM waston等更加推动了这一产业的深度发展,目前,市场上出现了各种各样的智能机器人。
智能机器人一方面给人们生活带来巨大的便利,另一方面也引出了一些新的技术课题,如问答系统、对话系统对文本分类算法。使用文本分类技术,能对大规模的文本信息进行处理,方便计算机对这些信息的学习。在文本分类算法中,朴素贝叶斯算法是经典的文本分类算法之一[1],近来,对朴素贝叶斯算法的研究热度不减,如 Escalante等[2]将增量朴素贝叶斯算法应用到视频的手势识别中,取得了较不错的效果;Dimkovski等[3]把朴素贝叶斯增量算法与神经网络进行相应的结合,提出了对生物学行为信号进行处理,并取得了预期的实验效果;Feng等[4]浅析了朴素贝叶斯增量算法基于词频关系集和主动学习理论,探讨了一种新的电子邮件分类方法,并通过在线应用证明了该理论的实用价值;董立岩等[5]分析了一种新的增量学习方法,通过将无标签文本加入到训练集中作为新的训练集,测试新训练集并训练所得的分类器有更好的分类效果,论证了该方法的有效性。这些最新的研究成果与关注说明了增量学习的朴素贝叶斯算法在相关领域依然有广泛的应用前景和研究焦点。
为了巩固和进一步强化朴素贝叶斯增量算法的研究,本文利用了朴素贝叶斯算法具有稳健性和简单高效的显著特点,这一算法的分类效果很大程度上依赖或受限于训练集样本的完备性。为了解决这一问题,学者们提出了一种增量学习方法[6~17],目的是提升朴素贝叶斯算法的分类效果与学习能力。当有新的样本出现时,可以通过增量学习对分类器进行更新,而不用重新对分类器进行训练。在充分利用与发挥朴素贝叶斯理论适应性前提下,合理应用增量学习算法属于动态的过程。在此基础上,本文提出了一种改进的朴素贝叶斯增量学习方法,将进一步提高增量学习的效果。此外,针对大量的未标注语料的增量学习,本文探讨了一个新的增量样本选择阈值,结合传统的增量样本选择阈值一起使用,使其起到更好的增量样本选择效果。
本文的主要贡献包括以下3个方面。
1) 在传统增量算法的基础上,提出一种对特征空间进行更新的改进增量算法,实验表明,改进的增量算法较传统的增量算法表现出更好的增量学习能力。
2) 在对无标注文档的增量样本选择中,提出了一个最小后验概率作为样本选择阈值,实验证明,该阈值结合类置信度阈值一起使用,能起到更好的增量样本选择效果。
3) 在对增量算法和增量样本选择方法的评价上,根据算法的设计目的和其他文献中的一些评价方法,总结并提出了增量算法和增量样本选择方法的几个评价指标,为衡量这些方法的效果提出了有效的评价方式。
2 相关方法与概念
为了后面章节内容的描述与算法及其理论应用,这里先介绍本文应用了的相关方法和概念,具体如下。
2.1 朴素贝叶斯算法
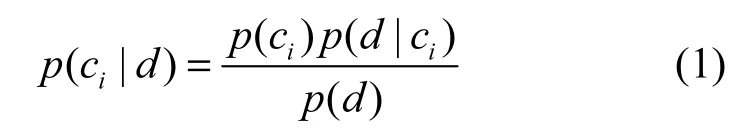
要确定文档d={t1, t2,…,tn}属于哪个类别,就计算d属于各个类别的概率。若哪个类别的概率较大,则d的分类结果就是对应的那个类别。在计算d属于各个类别的概率时,P(d)都是一样的。所以要使式(1)最大,只需要使分子最大即可。将其展开,结果所得如式(2)所示,这就是朴素贝叶斯分类器表达式。
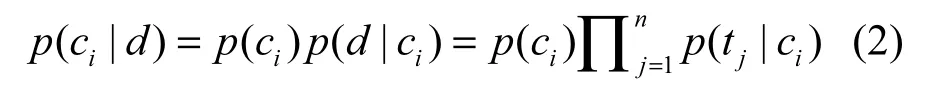
综合上述可知,在计算文档d属于哪个类别的概率时,只需要分别计算类别概率和特征的类条件概率。而目前主要有2种方法计算这2个概率,对应地分别产生了2种模型即多项式模型和伯努利模型。
2.2 多项式模型
因多项式模型的粒度是基于词的,其优点是考虑到每个词的出现次数,当对一个文档类别进行分类时,这个信息能够衡量与判断不同类别的文档关于词频率上的差异,因此,该模型对问句与文档分类有重要的参考价值。在使用多项式模型计算条件概率时,对应的 2个概率计算方法分别为式(3)和式(4)。类别概率为

特征的类条件概率为
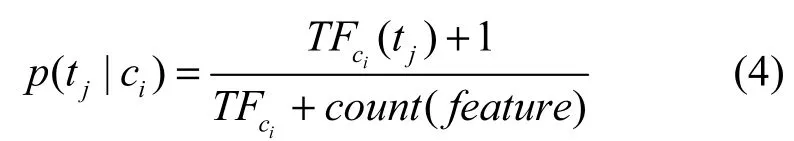
其中,count( ci )是类别ci的文档数,count( D) 是训练集的总文档数,TFci(tj)是特征tj在类别ci中出现的频次,TFci是类别ci的总词数,count(feature)是特征空间的维数。为了避免其他属性含有的信息在训练集中未出现的属性值被“抹去”,在计算概率值时通常进行“平滑”,则对分子加一和分母加特征维数都是对该概率计算的修正,以免出现分子或分母为0的情况。
2.3 伯努利模型
伯努利模型的粒度是基于文档的。伯努利模型的类别概率计算方式与多项式模型是一致的。不同的是特征的类条件概率计算方式。伯努利模型的特征类条件概率计算方式如式(5)所示。

其中,DFci(tj)是类别ci中出现特征tj的文档数,DFci是类别ci的文档总数。类似于多项式模型,分子上加0.01是对该概率计算的修正。本文改进的贝叶斯增量算法就是使用伯努利模型进行计算的。
2.4 朴素贝叶斯增量算法
朴素贝叶斯分类算法是一种有监督的学习分类算法,贝叶斯分类算法的预测能力与训练语料的完备程度息息相关,训练语料越完备,其预测能力越强,泛化能力也越强。在实际应用中,分类器的训练语料集有一个逐渐完备的过程,很难一蹴而就。对于这种情况,传统的做法是采用一批已经清洗和标注完成的语料对分类器进行训练,在训练集语料有更新的时候,就对分类器重新进行训练。但是这种做法导致时间与计算成本浪费较多。
针对朴素贝叶斯分类算法存在上述的不足,学者们提出了一种增量学习的朴素贝叶斯算法来进行弥补。增量学习算法一般有2种形式:1) 有标注语料的增量,在初次训练后,再次收集一批新的人工标注语料,然后将这批语料批量新增用于更新分类器;2) 无标注语料的增量,在分类器使用过程中,对未识别的语料进行分类,根据自动分类的类别将该语料加入到训练集以更新分类器。
在无标注语料的增量中,显然并不是所有的未识别语料都能用来更新分类器的,因为分类器初始分类效果不好,肯定会有分类错误的情况出现,用分类错误的语料更新分类器只会使分类效果更差。因此,需要对这些分类语料进行合理筛选,筛选用于更新分类器的语料。对此,本文方法借鉴了罗福星[6]提出的置信度阈值,根据该阈值判断某文档是否适合进行增量学习。置信度阈值也叫类置信度,也就是在分类完成时,计算所得该文档属于每个类别的概率。要使该文档属于分类结果类别的概率大于属于其他类别的概率和的某个倍数,才是可信、可增量的。倍数越大,要求越严格,此倍数在本文中称为增量系数。一般来讲,当初始训练样本较少时,分类效果一般,可以将增量系数设置地较大,以筛选更为可信的样本;当训练样本较多时,分类效果更好,可以将增量系数设置得较小,也可以筛选出可信的样本,以扩大样本数量。本文参考和借鉴罗福星等[6~17]的计算公式,如式(6)所示,iθ是语料属于类别i的概率,tθ是分类器分类结果类别的概率。

在筛选所需要进行增量更新的样本后,将该样本添加到训练集中,并对分类器进行增量更新。假设增量的文本属于类别ci,需要更新各类的类别概率和特征的类条件概率计算式分别为式(7)和式(8)[6~17],文档数量更新定义为式(9)和式(10)。

其中,D为训练集文档总数,DC为类别C的文档数量,DC(tc)为类别C中出现特征tc的文档数量。本文仅对概率和文档数量进行更新的增量方法称为传统增量学习方法。
3 改进的朴素贝叶斯增量算法
现有的朴素贝叶斯增量学习算法在进行增量学习时,仅对类先验概率和原有的属性概率进行修改。但在新增的文本当中,非常可能会有新的特征存在,如“萌萌哒”一词是网络类文章非常好的一个辨别特征,如果在训练集中没有这个词的存在,这个词当然不会被选为特征的;而若增量的文本中含有这个词,这个词将对分类产生较好的影响,因此,有必要在增量时将这个词添加到特征列表中,然后对相关概率进行重新计算。
基于此,本文对现有增量学习算法进行改进和优化,在对类概率和原有属性概率进行修改的同时,将新出现的特征加入到特征空间。选择初次训练时没有考虑的优秀特征,扩大分类的特征空间,对全新语料有更好的适应能力,提高问句分类准确率,以其达到更好的增量学习效果。
3.1 新增特征选择
在改进的朴素贝叶斯增量算法中,本文所采用方法与其他研究方法的最大区别是对特征空间进行更新。本文对特征空间进行更新的增量方法称为改进的增量学习方法,对于新增特征的更新方法如下所示。
1) 在改进的增量学习算法中,需要分别更新类别概率、特征的类条件概率。假设增量的文本属于类别ci,类别概率、特征的类条件概率更新计算公式分别与式(7)~式(10)一致。
2) 若有新增特征选择,则更新新增特征的类条件概率。本文假设增量的文档含有新的特征,则该新特征的类条件概率计算式如式(2)所示。
下面分析在什么情况下进行更新。对于新增特征的选择,本文认为当分类器进行学习时,与特征选择的依据有关。在学习分类器时需要对新文本中的特征进行相应判断和筛选,若条件符合,则把新文本作为新特征加入特征空间。本文将以问题集语料作为实验数据进行验证,由于在对问题集分类的特征空间进行构建时,没有对特征空间进行降维处理,而对于特征的选择,与特征出现的频率或其文档频率无关。因此,在新的问题语料进入分类时,只需要判断处理后的语料是否存在特征空间中没有的特征。如存在,则进行特征空间的更新,再对相应的参数进行修改;否则,仅需对特定特征和类别的参数进行修改。
3.2 无标注增量文本选择
对于无标注语料中增量文本的选择,本文参考了罗福星[6]提出的置信度判断方法。该方法将贝叶斯分类器的分类概率作为判断依据,称为类置信度,类置信度的计算方法与公式详见2.4节。本文提出了一个以最小后验概率作为另一个阈值对文本进行筛选,使用了类置信度作为阈值筛选增量文本。最小后验概率的计算方法为式(11)。本文在借助类置信度阈值对增量文本进行筛选时,该方法不但充分地利用了类别区分度进行判断,而且解决了其他方法中未考虑单类别分类概率的不足与缺陷。

此阈值的计算方法是以贝叶斯分类器计算文本属于各类的后验概率公式为基础的。其中avg(maxIndexTermCount)是分类器所分类别的特征平均文档频次;termNum是待分类句子中含有特征空间中特征的数量;allcount是文档总数;class(maxIndex)是分类器所分类别的文档数量;β是最小后验概率方法的增量系数,通过β来调整阈值的大小。考虑到选择增量样本时,直接按照特征平均文档频次来进行计算显然是不够的,因特征的文档频次越高,样本属于该类的概率也就越大,所以将通过改变增量系数选择对应的样本进行增量学习。
3.3 无标注语料增量算法
本文提出的无标注语料增量算法思想与实现流程如下,参阅了张智敏等[7~16]的增量学习思路。
假设输入:训练集D,测试集Dt。
Step1使用训练集D贝叶斯分类器进行学习。
Step2使用学习好的贝叶斯分类器对测试集Dt的每个文本进行分类。若分类结果符合设定阈值,则转 Step3;否则,返回分类结果并进行下一个文本的分类。
Step3将新增文档表示为:d={t1, t2,…,tn, tn+1},t1至tn为原特征空间t={t1, t2,…,tn}存在的特征,tn+1为符合条件的新增特征。若tn+1不为空,则转Step4;否则,跳过Step4直接转Step5。
Step4将新增特征添加到特征列表中,计算该特征在每个类别中的条件概率P( tn+1|ci),并且后续分类语料需考虑新增特征的影响。
Step5分别更新测试集。文本中存在与原特征列表中特征的条件概率P(tn|ci)、类别概率P(ci)、训练文档数量和类别文档数量。
Step6算法结束。
3.4 有标注语料增量算法
本文构建的有标注语料增量算法思想与实现流程如下,参阅了张智敏等[7~16]的增量学习思路。
假设输入:训练集D,增量集Dt。
Step1使用训练集D对贝叶斯分类器进行学习。
Step2对于增量集Dt文档逐个进行处理,执行 Step3~Step5。
Step3将增量集Dt文档表示为:d={t1,t2,…,tn, tn+1},t1至tn为原特征空间t={t1,t2,…,tn}存在的特征,tn+1为符合条件的新增特征。若tn+1不为空,则转Step4;否则,跳过Step4直接转Step5。
Step4将新增特征添加到特征列表中,计算该特征在每个类别中的条件概率P(tn+1|ci)。
Step5分别更新测试文本中存在与原特征列表中特征的条件概率P(tn|ci)、类别概率P(ci)、训练文档数量和类别文档数量。
Step6 算法结束。
3.5 增量算法评价指标
据悉,学术界至今未形成一套标准和规范化的增量算法评价方法,大部分研究者都是以增量算法的效率评价增量算法可行性,但未以增量算法的效果评价增量算法优越性。本文要评估增量算法的优劣性,需要从增量算法的设计初衷考虑。首先,增量算法在算法运行过程中对算法进行增量学习,因此,必须考虑算法的效率,否则将影响分类算法的运行效率。其次,在保证时间与空间效率的前提下,增量算法的运行效率采用尽可能多的信息对分类器进行优化,即使用增量算法进行增量是通过对原有算法的训练集进行扩展,从而提高分类器对更多待分类文本的识别能力,并提高分类器的泛化能力。本文从2个维度浅析增量算法的评价指标。
1) 有标注语料增量方法评价指标。首先,定义并说明如下概念与参数。① P(all)定义为直接用所有训练文档训练出的分类器对测试集进行分类所得的准确率。② P(orignal)定义为用部分训练集语料训练出的分类器对测试集进行分类所得的准确率。③ P(increment)定义为用初始训练后剩余的训练集语料对分类器进行增量学习后对测试集进行分类所得的准确率。
针对有标注语料增量方法评价指标,本文设计2个评价指标:① 比较使用增量算法进行增量学习前后对待分类信息的识别程度,通过计算增量学习前后的准确率的差值进行评价,本文称之为增量学习力(ILB, incremental learning ability),数学计算式表示为ILB=P(increment)−P(orignal)。ILB值越高,表示增量学习能力越强;② 比较使用增量算法进行学习和直接使用所有语料对分类器进行训练的信息差别,通过计算直接训练和增量学习分类准确率的差值进行评价,(DLB, difference learning ability),数学计算式表示为:DLB=abs(P(all)−P(increment))。DLB值越小,说明增量学习与直接训练得到的分类器越接近,表明增量学习丢失或损失的信息就越少。
通过本文实验验证和数据分析,本文发现第 1个评价指标直观反应了增量学习前后分类器的识别信息能力变化,但是忽略了分类器通过拟合可能性的存在,证明了增量学习对于初始训练集数据信息的过渡学习,但第2个评价指标能较好地避免出现此情况。因此,综合这2个评价指标,能较好和有效地对增量学习算法进行评价。
2) 无标注语料增量方法评价指标。本文采用阈值对未标注文本进行增量选择,这直接关系到未标注语料增量算法的准确率。为达到更好效果,需判断选择效果的优劣,首先需要考虑选择的文本是否准确,因为在进行增量学习时,使用阈值进行增量选择后再根据分类器对分类文本的类别划分,将文本增量学习到某个具体类别中。因此,需尽量选择分类器分类准确的文本进行增量学习。这样可以借用分类器中的2个通用概念即准确率和召回率对阈值的选择正确性进行判断。为了更好地与其他文献进行区分,本文将这2个具体概念称为增量准确率(用P表示)和增量召回率(用R表示)。

通过后面实验验证与数据分析可知,在选择增量文本时,增量准确率是首要考虑因素。在本文实验验证过程中,当一个文本被选为增量文本时,对比其增量目标类别和实际的类别(即标注的类别),若两者一致,则认为增量选择是正确的。如果在增量准确率一致的情况下,哪种方法的效果更好。在使用不同阈值对增量文本进行选择时,既要考虑到增量文本选择的准确性,又要保证增量召回率尽可能高。若增量召回率越高,则说明在同等情况下学习到的样本就越多,增量学习的效果就越好。因此,在同样增量准确率前提下,必须对增量召回率的大小进行比较。
4 实验方法与数据分析
传统增量算法普遍都是仅对概率和文档数量进行更新的增量算法,基于此,本文提出了改进的增量算法除了对概率和文档数量进行更新外,还对特征空间进行更新。为了证明本文改进的朴素贝叶斯增量算法优越性,本文分别设计了有标注语料增量算法实验和无标注语料增量算法实验这2组实验数据进行验证和分析,其中,有标注语料增量算法实验是通过增量算法进行增量学习的分类器和直接采用所有训练集进行学习的分类器差别与传统的增量算法和改进的增量算法的差别进行比较与分析;无标注语料增量算法实验是通过传统的增量算法与改进的增量算法的增量准确率和增量召回率进行比较与分析。
4.1 有标注语料增量算法验证
4.1.1 实验设计
本文使用哈尔滨工业大学的问题分类语料进行实验验证,根据哈尔滨工业大学信息检索实验室提供的数据,该语料共划分为7大类和85小类,总语料数达到6294条,其中,1314条为测试语料,4980条为训练语料。
本文就增量算法进行实验过程中直接训练是指将4980条语料全部作为训练集对分类器进行学习,而后使用1314条测试语料进行分类实验,从而得出分类准确率。而增量学习实验,以训练语料按照 9∶1比例进行划分而进行实验,实验随机对4980条语料按类均分为10份,其中,9份作为初始训练集,1份作为增量学习数据集,具体各类别语料数量如表1所示。实验先使用初始训练集对分类器进行学习,而后使用1314条测试语料进行测试实验,从而得出分类准确率。再分别使用传统增量和改进增量2种方法进行实验,使用增量学习数据集对分类器进行增量学习,然后再一次性使用1314条测试语料进行测试实验,从而得出增量学习后的分类准确率。在 1∶9比例进行划分中,1份作为初始训练集,9份作为增量学习数据集。
4.1.2 实验数据
采用 4.1.1节中的实验设计方法,采用多种训练语料进行比例划分,接着分别进行实验,各实验问句数量分布如表1所示。实验中使用各种方法进行分类所得的准确率如表2。将表2中实验数据绘制折线图则如图1所示,横坐标表示表2中的9个实验数据,数据顺序与表2一致。将初始训练、传统增量和改进增量分类准确率与直接训练所得分类准确率的差值如图2所示。
4.1.3 数据分析
实验设计的数据即如表1所示是按照初始训练语料数量由多到少进行排序的,从表1和图1中的初始训练数据文本发现,在使用朴素贝叶斯分类器进行分类时,初始训练语料越多,分类准确率越高,反之初始训练语料较少,则分类器的效果明显受到影响;在增量学习的分类器准确率与直接训练的越接近时,则说明了增量学习算法所得到分类模型与直接训练的分类模型越接近,增量效果越好。本文增量学习算法实验基于此前提进行验证和设计的。
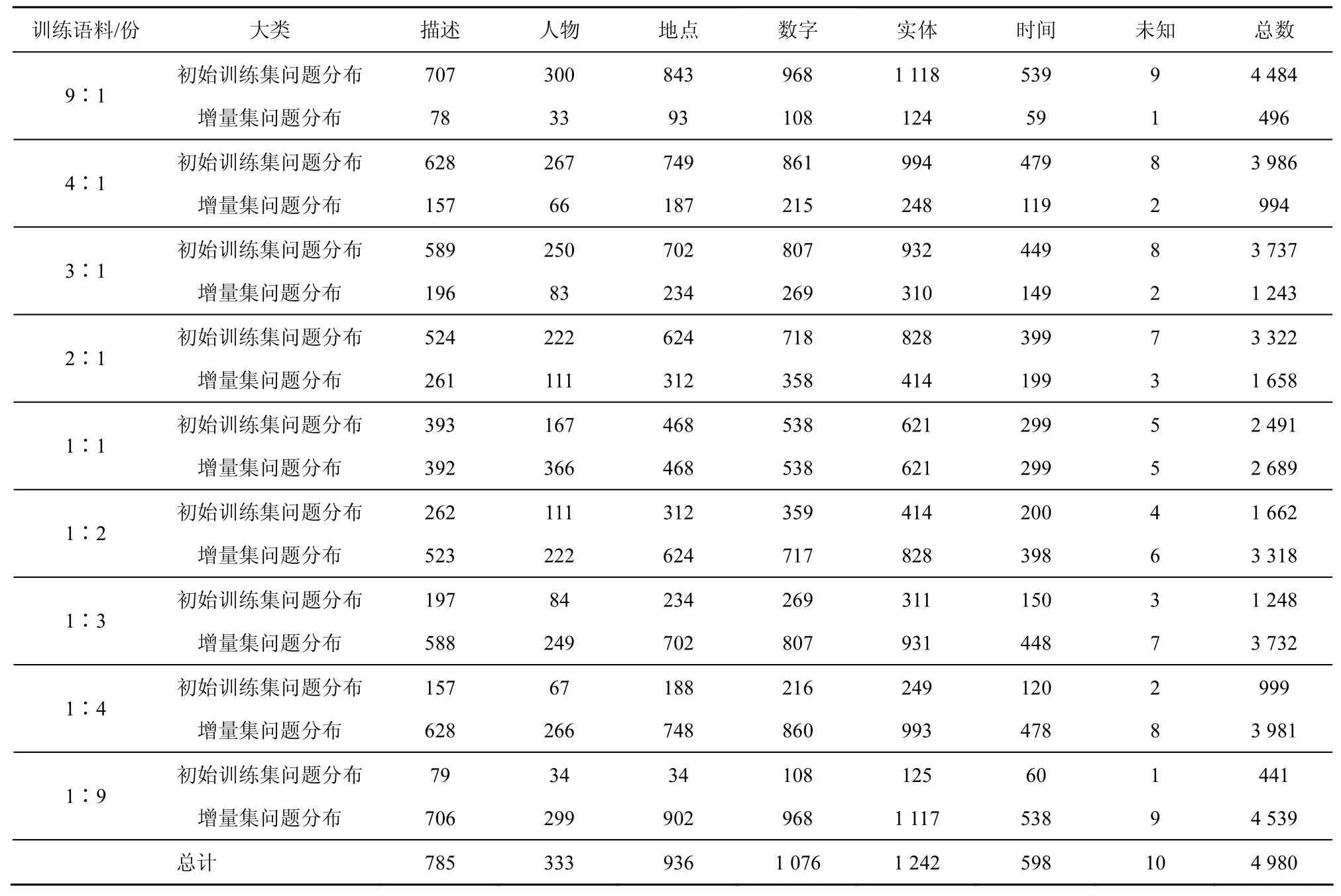
表1各实验问句数量分布
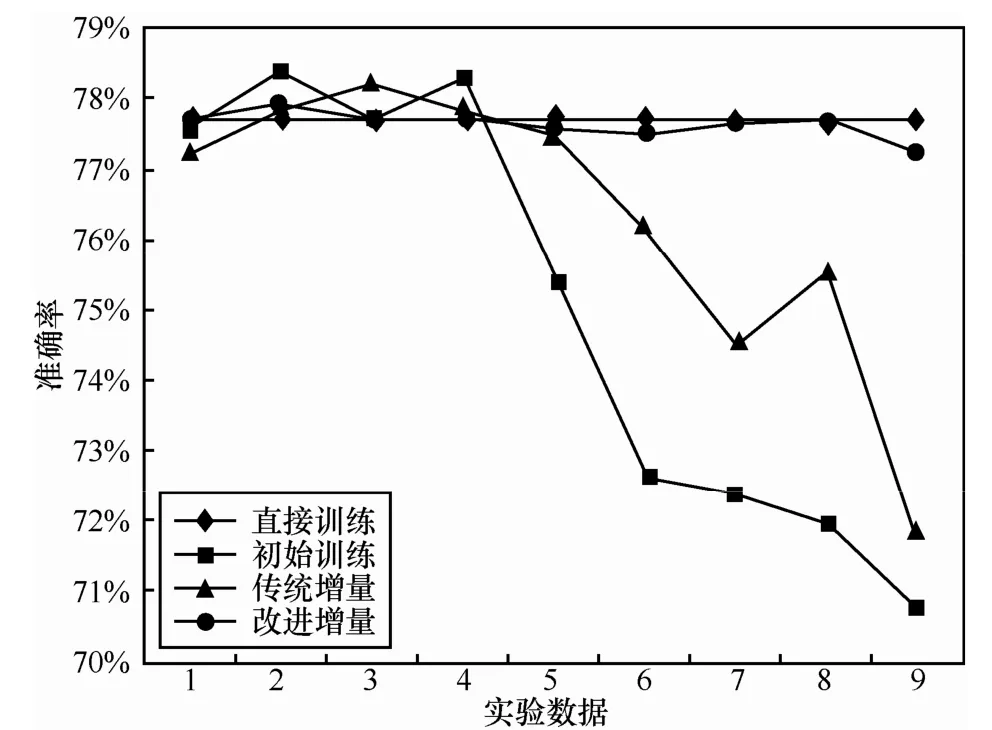
图1有标注语料增量学习准确率折线

表2有标注语料增量学习结果

图2分类准确率差值对比
首先,从第一个评价指标进行分析,根据表2和图1数据发现,对比2种增量学习算法增量后所得的分类准确率和初始训练所得的分类准确率。在初始训练集数量较少的时候,如表2后 5个实验和图1所示,每个数据的增量算法都对分类器起到了很好的增量学习效果,并且改进后的增量算法增量学习效果更佳,显然初始训练集语料越少,增量学习效果越明显。因此,说明了改进增量算法的增量学习效果较传统增量方法更好。
如表2前4个实验数据和图1所示,增量学习后分类器分类效果比初始训练分类器分类效果更差的数据,下面分析该现象导致的原因和第2个有标注语料增量算法评价指标。朴素贝叶斯分类算法的预测能力很大程度上依赖于其训练集的优劣,若训练集越优秀,其语料越丰富,贝叶斯分类算法的预测能力也就越强。但是在实际应用中,假设训练集的语料都是优质的,这样保证了所有训练分类器的分类效果尽可能得好,选择的语料也尽可能优秀。因此,优质语料越多,训练出来的模型就越好,泛化能力越强。在本组实验过程中,直接训练使用了全部的训练语料进行训练,则直接训练所得到的模型也是最优的。
其次,分析图2的初始训练、传统增量和改进增量方法与直接训练的分类准确率差值柱形图,差值是用直接训练所得的分类准确率减去其他方法所得的分类准确率。若差值为正值,则说明直接训练所得的分类准确率更高差值,若差值为负值,则说明非直接训练的分类准确率更高。上述已阐述了直接训练所得的模型是本组实验中最优的模型,其他模型与该模型的差距越小,则说明该模型越好,在图2中具体表现为柱形的长度越小,则说明该模型与最优模型的差距越小。从图2中发现:1) 改进增量方法与最优模型的准确率差值基本上是最小的,准确率差值均在0.05%以下;2) 传统增量算法对分类器起到较好的增量学习作用,在一定程度上缩小了使用部分训练集进行学习的分类器与最优分类器的差距,该结论在后面实验中表现效果更为明显。由此可见,改进的增量学习算法较传统的增量学习算法增量学习效果更好。
再次对训练语料 4∶1份和训练语料 9∶1份的 2个实验进一步分析并且可知,初始训练的语料数量较直接训练要少,所得分类准确率却更高,从图 2中发现对应的柱形是负值。但是假设直接训练的语料越多,其训练所得的模型应当是更好。由于直接训练的模型较初始训练的模型更好,初始训练所得的模型在测试实验中分类准确率却更高,则有可能是初始训练的模型对测试集产生了过拟合的现象,也就是初始训练的模型虽然在测试集测试中表现更好的预测能力,但是其泛化能力却有所欠缺。此时,增量算法对其进行纠正。虽然在实验中的增量算法分类准确率较初始训练要低,但是从图2中发现,增量学习后的模型与最优模型的差距较初始训练的差距已经缩小了。因此,说明了增量算法对朴素贝叶斯分类器的过拟合问题能起到较好的修正作用。同样表明,改进后的增量学习算法的修正作用较传统增量算法更好。
4.2 无标注语料增量算法验证
4.2.1 实验设计
本文同样使用哈尔滨工业大学的问题分类语料进行实验验证,根据哈工大信息检索实验室提供的数据,该语料共划分为7大类和85小类,总语料数达到6294条,其中,1314条为测试语料,4980条为训练语料。
在本组实验设计中,需要根据阈值选择的不同分别进行3个实验:1) 使用类置信度为阈值进行实验;2) 使用最小后验概率为阈值进行实验;3) 同时结合类置信度和最小后验概率为阈值(本文称为双阈值)进行实验。在各实验中,本文将对增量学习算法测试在各阈值就不同的取值情况下的增量准确率和增量召回率进行计算,然后对其所得的实验结果进行对应的分析。
4.2.2 实验数据
1) 使用类置信度为阈值进行实验。类置信度的计算如式(6)所示,本实验中对增量系数α选择不同的取值,则得到不同的增量样本选择结果,具体实验结果如表3所示。
2) 使用最小后验概率为阈值进行实验。最小后验概率的计算如式(11)所示,本实验中对增量系数β选择不同的取值,则得到不同的增量样本选择结果,具体实验结果如表4所示。
3) 同时结合类置信度和最小后验概率为阈值(即双阈值)进行实验。考虑到类置信度和最小后验概率这2个系数组合与选择有多种不同形式,本实验仅以其中一些组合为例进行验证,选择最小后验概率的增量系数β固定取值为3,类置信度的增量系数α随机定为不同的取值为例,具体实验结果如表5所示。
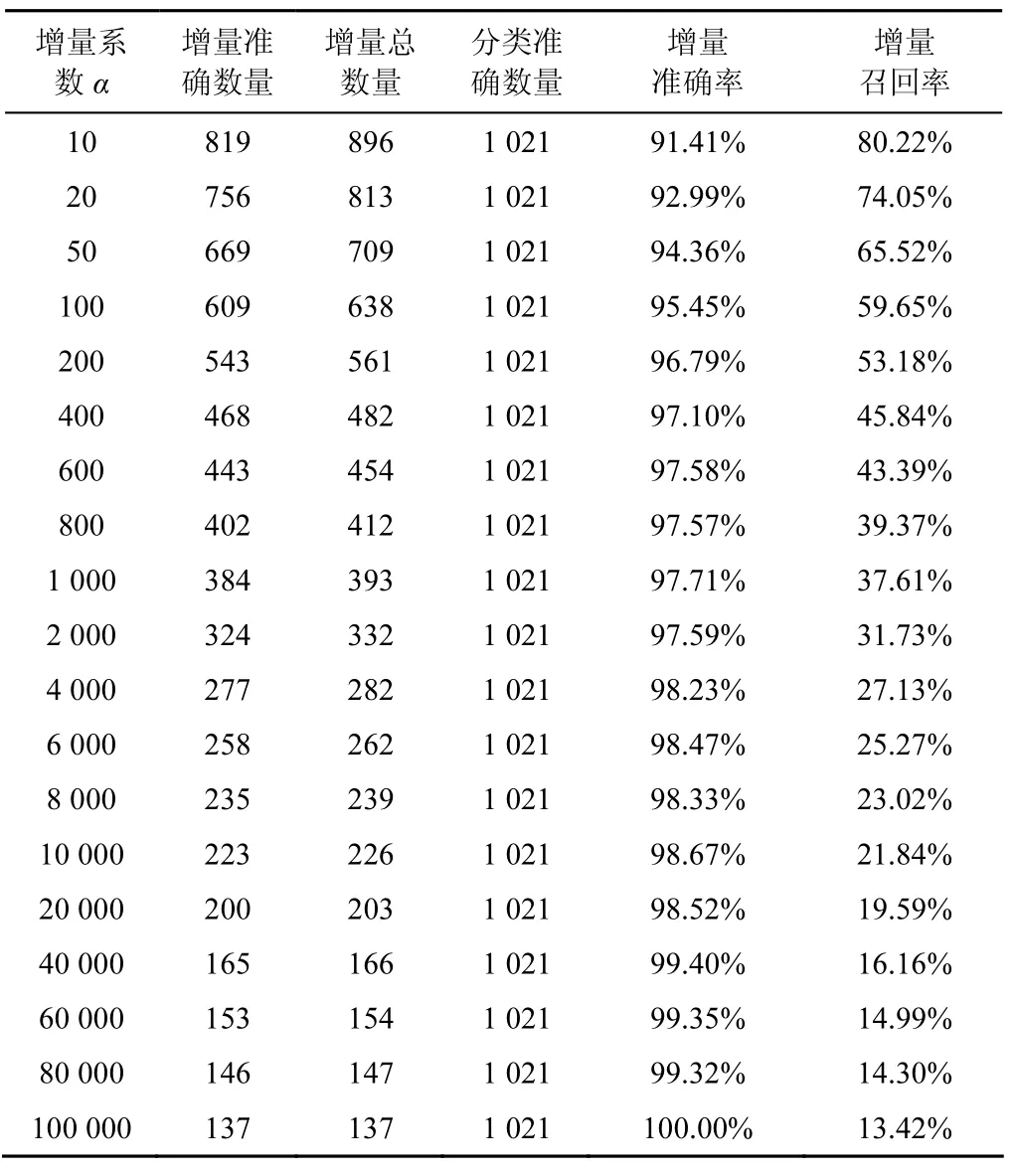
表3类置信度阀值增量样本选择情况

表4最小后验概率阈值增量样本选择情况

表5双阈值增量样本选择情况
4) 当类置信度、最小后验概率和双阈值的增量准确率分别达到 98%、99%和 100%进行实验时,其所得的最高增量召回率数据详见具体实验结果如表6所示。

表6增量召回率比较
4.2.3 实验分析
首先,从表3类置信度的实验数据发现,使用类置信度作为增量样本选择阈值起到较好的效果作用,使增量准确率较高和增量召回率保持在一个理想状态值。当增量系数达到一定值时,其增量准确率达到近 100%,这对增量样本的选择起到不错的效果,并且作为单独的增量样本选择阈值也起到较好的效果。
其次,从表4可以看出以最小后验概率作为样本选择阈值的实验数据可知,使用最小后验概率作为增量阈值选择增量样本的效果较类置信度阈值差,增量准确率大多数保持在 80%~90%。当增量准确率保持较高值时,其增量召回率下降较明显,但是当增量系数达到一定程度时,其增量准确率也达到100%。因此,说明最小后验概率本身可以单独作为一种增量阈值进行使用,仅是增量召回率不太理想。
再者,为了解决最小后验概率本身单独使用效果不理想的问题,本文一方面将采用最小后验概率与类置信度两者进行组合的方法解决该问题。现选择最小后验概率的增量系数 β=3,类置信度的增量系数α值为变量时的实验结果数据如表5所示,这2个增量阈值结合使用的效果较为理想,最低的增量准确率达到98.66%,并且对错误文本的选择有很好的识别效果。
本文另一方面也将采用双阈值的方法进行增量样本选择并且与类置信度单独使用作为阈值进行相比较。首先比较两者之间的增量准确率和增量召回率,当双阈值最低增量准确率为98.66%时,其增量召回率为28.80%,然而当单独使用类置信度阈值增量准确率为 98.67%时,其增量召回率为21.84%。反之,当选择以98%作为单独的一档时,并且单独使用类置信度阈值进行增量样本选择,所得的增量准确率达到 98%,增量召回率最高为27.13%,略低于双阈值的增量召回率。当选择使用双阈值进行增量样本选择时,一旦增量准确率保持99%以上,增量召回率也均保持20%以上,但是单独使用类置信度作为阈值增量召回率均低于20%。本文发现,在实验中对分类算法的增量样本进行选择时,增量准确率非常最重要,只要增量样本中有一个错误样本,则这个错误样本会一直伴随分类算法,对其分类结果产生副作用。当增量学习的样本选择增量准确率达到 100%时,再比较两者之间的增量召回率。从表6中的数据发现,当增量准确率达到 100%时,使用双阈值进行增量样本选择的增量召回率为最高且达到了18.61%,说明这个增量准确率值已取得非常好的效果并足以在实际业务中应用;而单独使用类置信度作为阈值的增量召回率达到13.42%;仅以最小后验概率作为阈值的增量召回率仅是1.76%,即该效果较不理想。
综合上述实验结果与分析表明,使用双阈值的增量样本选择方法效果最佳,比单独使用类置信度作为阈值对未标注语料增量算法的识别效果更好。即使以最小后验概率作为单独增量样本选择阈值效果较差,但是最小后验概率对类置信度仍起到较好的补充作用。当过滤含有极少部分类置信度的增量系数较小时不能识别的错误样本,并且采用不同的类置信度阈值的样本选择机制,将有效提高增量召回率。
5 相关工作
随着人工智能技术的快速发展,产业界对智能机器人的持续升温,为了提升问答系统准确率,作为高效而简单实用的算法之一,朴素贝叶斯增量算法作吸引了大量科研工作者的关注,并产生了一批与朴素贝叶斯增量算法相关的研究。
在朴素贝叶斯增量算法方面,Read等[17]提出了批量增量算法和单篇增量算法这2种对分类算法的增量方法,并将两者进行了相关比较,分析了2种增量算法的优劣特点与适用范围,对这2种增量方法的具体应用提出了有益的参考观点,本文的有标注语料增量算法即属于批量增量算法,而无标注语料增量算法则属于单篇增量算法。Gu等[18]分析了本文中除了特征词之外的其他信息,比如语义信息与语法信息,并且提出了在对分类器进行增量学习时,这些信息也需要考虑纳入范围之内,从而提高了增量学习的效果。
在增量样本和组合分类器方面,近几年,不但许多学者关注对机器学习组合分类器相关研究,而且对增量学习如何进行增量文本的选择研究也持续走高。Muhlbaier等[19]即使发现了一种新的组合分类器增量学习方法,而且有效地解决了原有增量方法存在的问题,特别是对无标注语料增量样本的选择起到更好的效果作用。Bouguelia等[20]应用了组合分类器理论,通过实验证明与发挥了组合分类器的优势。还有一些学者将研究内容与精力聚焦在增量学习算法的其他相关方面研究。比如Fong等[21]探讨了增量学习之前对增量学习内容进行预处理。他们关注了分类器训练前需要对训练内容进行预处理,同样也关注了增量学习前对增量学习的内容进行预处理的效果,并且提出了增量学习算法预处理的实用方法与注意事项。
但是,以上这些研究都有一定局限性,例如像Eyheramendy、Lewis、Madigan 等[22~26]对朴素贝叶斯分类器在某些假设情况下得到不错的性能与分类效果。然而,他们仅是侧重于增量学习算法本身的某个方面,并没有涉及到对特征空间的增量样本更新、无标注语料增量算法阈值选择策略的研究;在对增量算法进行实验验证与分析时,绝大多数实验分析仅是从分类的准确率角度进行比较,而没有从增量学习算法目的层面进行深入着手和深度分析。本文对上述内容进行了重点研究,这些研究对朴素贝叶斯增量算法对于自然语言处理技术应用于智能机器人这一工作将有重要的实用意义。
6 结束语
本文从朴素贝叶斯分类算法出发,寻找对其进行增量学习的改进方法。改进的增量学习方法在传统增量算法的基础上引入了新增特征的增量学习。实验证明,改进的增量学习方法在一定程度上解决了朴素贝叶斯分类算法的过拟合问题,增量学习接近与直接使用所有文本进行分类的分类器,学习效果较传统方法更好。
此外,本文针对无标注文本的增量学习,提出了以一个最小后验概率作为增量样本选择阈值。实验证明,虽然该阈值单独使用时增量召回率较低,效果较不理想,但是该阈值能对传统的类置信度阈值起到较好的补充作用,而且结合类置信度阈值,在同样达到 100%增量准确率情况下,使用双阈值进行增量样本选择增量召回率比单独使用类置信度阈值提高了5个百分点,取得了较好的效果。虽然朴素贝叶斯增量学习算法学术界研究起步早且取得一些成果,但是在适应性与产业化方面尚有更深入的研究空间,其中,对改进的增量学习方法,现有处理方法仅适用于问题分类中,对于使用特征选择用于特征空间进行处理的方法,是否包括不限于特征的增量选择还有待探讨。而对于未标注语料选择方面,如使用服务领域的航空常见问题集与答案集进行增量样本的选择,如何在保证增量准确率的同时提高增量召回率也是下一步研究的方向之一,这些研究将进一步巩固和延伸朴素贝叶斯增量算法的科研实用价值。
[1]CHRISTOPHER M. Pattern recognition and machine learning[M].New York: Springer, 2006.
[2]ESCALANTE H J, MORALES E F, SUCAR L E. A Naive Bayes baseline for early gesture recognition[J]. Pattern Recognition Letters,2016, 73: 91-99.
[3]DIMKOVSKI M,AN A. A Bayesian model for canonical circuits in the neocortex for parallelized and incremental learning of symbol representations[J]. Neurocomputing, 2015, 149: 1270-1279.
[4]FENG L,WANG Y,ZUO W. Quick online spam classification method based on active and incremental learning[J].Journal of Intelligent amp;Fuzzy Systems,2015,30(1):17-27.
[5]董立岩, 隋鹏, 孙鹏, 等. 基于半监督学习的朴素贝叶斯分类新算法[J]. 吉林大学学报: 工学版, 2016(03).DONG L Y, SUI P, SUN P, et al. Novel Naive Bayes classification algorithm based on semi-supervised learning[J]. Journal of Jilin University, Engineering and Technology Edition, 2016(03).
[6]罗福星.增量学习朴素贝叶斯中文分类系统的研究[D].长沙:中南大学,2008.LUO F X. Research on incremental learning naive Bayesian classification system[D]. Changsha: Central South University, 2008.
[7]张智敏. 基于增量学习的分类算法研究[D]. 广州: 华南理工大学,2010.ZHANG Z M. The study of classification based on incremental learning[D]. Guangzhou: South China University of Technology, 2010.
[8]侯凯. 加权贝叶斯增量学习中文文本分类研究[D]. 长沙: 长沙理工大学, 2013.HOU K. The weighted Bayesian incremental learning Chinese text classification study[D]. Changsha: Changsha University of Science amp;Technology, 2013.
[9]李金华, 梁永全, 吕芳芳. 一种加权朴素贝叶斯分类增量学习模型[J]. 计算机与现代化, 2010, 2010(5): 30-32.LI J H,LIANG Y Q, LV F F. An incremental learning model of weighted Naive Bayesian cassification[J].Computer and Modernization, 2010, 2010(5): 30-32.
[10]罗福星, 刘卫国. 一种朴素贝叶斯分类增量学习算法[J]. 微计算机应用, 2008, 29(6): 107-112.LUO F X,LIU W G.An incremental learning algorithm based on weighted Naive Bayes classification[J].Microcomputer Applications,2008, 29(6): 107-112
[11]宫秀军, 刘少辉, 史忠植. 一种增量贝叶斯分类模型[J]. 计算机学报, 2002, 25(6): 645-650.GONG X J,LIU S H,SHI Z Z. An incremental Bayes classification model[J]. Chinese Journal of Computers, 2002, 25(6): 645-650
[12]高洁, 吉根林. 一种增量式Bayes文本分类算法[J]. 南京师范大学学报(工程技术版), 2004, 4(3): 49-52.GAO J, JI G L. Incremental Bayes text categorization algorithm[J].Journal of Nanjing Normal University(Engineering and Technology),2004, 4(3): 49-52.
[13]王小林, 镇丽华, 杨思春, 等. 基于增量式贝叶斯模型的中文问句分类研究[J]. 计算机工程, 2014, 40(9): 238-242.WANG X L, ZHEN L H,YANG S C, et al. Chinese question classification research based on incremental Bayes model[J]. Computer Engineering, 2014, 40(9): 238-242.
[14]段华. 支持向量机的增量学习算法研究[D]. 上海: 上海交通大学, 2008.DUAN H. Study on the incremental learning algorithms for support vector machines[D]. Shanghai: Shanghai Jiao Tong University, 2008.
[15]姜卯生, 王浩, 姚宏亮. 朴素贝叶斯增量学习序列算法研究[J]. 计算机工程与应用, 2004, 40(14): 57-59.JIANG M S, WANG H, YAO H L. Studies on incremental learning sequence algorithm of Naive Bayesian classifier[J]. Computer Engineering and Applications, 2004, 40(14): 57-59
[16]ZHANG H, SHENG S. Learning weighted Naive Bayes with accurate ranking[C]//Fourth IEEE International Conference on Data Mining.2004: 567-570.
[17]READ J, BIFET A, PFAHRINGER B, et al. Batch-in cremental versus instance-incremental learning in dynamic and evolving data[C]// International Symposium on Intelligent Data Analysis. Springer Berlin Heidelberg, 2012: 313-323
[18]GU P,ZHU Q S,ZHANG C.A multi-view approach to semi-supervised document classification with incremental Naive Bayes[J]. Computersamp; Mathematics with Applications, 2009, 57(6): 1030-1036.
[19]MUHLBAIER M D, TOPALIS A, POLIKARO R. NC: combining ensemble of classifiers with dynamically weighted consult-and-vote for efficient incremental learning of new classes[J].IEEE Transactions on Neural Networks, 2009, 20(1): 152-168.
[20]BOUGUELIA M R, BELAÏD Y, BELAÏD A. A stream-based semi-supervised active learning approach for document classification[C]//201312th International Conference on Document Analysis and Recognition.IEEE, 2013: 611-615.
[21]FONG S, BIUK-AGHAI R P, SI Y, et al. A lightweight data preprocessing strategy with fast contradiction analysis for incremental classifier learning[J]. Mathematical Problems in Engineering, 2015, 2015:1-11.
[22]EYHERAMENDY S, LEWIS D D, MADIGAN D. On the Naive Bayes model for text categorization[J/OL]. https://core.ac.uk/display/21543464, 2003.
[23]PEDRO D, MICHAEL P. On the optimality of the simple Bayesian classifier under zero-one loss[J]. Machine Learning, 1997, 29:103-130.
[24]ANDREW M C, KAMAL N. A comparison of event models for Naive Bayes text classification[J]. In AAAI-98 Workshop on Learning for Text Catego, 2009, 62(2): 41-48.
[25]AY N, JORDAN M. On discriminative vs generative classifiers: a comparison of logistic regression and Naive Bayes[J]. Advances in Neural Information Processing Systems, 2002, 2(3): 169-187.
[26]ZHANG H. The optimality of Naive Bayes[C]//The Seventeenth International Florida Artificial Intelligence Research Society Conference. Miami Beach, Florida, USA, 2004: 562-567.
Improved incremental algorithm of Naive Bayes
ZENG Shui-fei1, ZHANG Xiao-yan1,DU Xiao-feng2, LU Tian-bo1
(1. School of Software Engineer,Beijing University of Posts and Telecommunications,Beijing 100876, China;2. School of Computer,Beijing University of Posts and Telecommunications,Beijing 100876, China)
A novel Naive Bayes incremental algorithm was proposed, which could select new features. For the incremental sample selection of the unlabeled corpus, a minimum posterior probability was designed as the double threshold of sample selection by using the traditional class confidence. When new feature was detected in the corpus, it would be mapped into feature space, and then the corresponding classifier was updated. Thus this method played a very important role in class confidence threshold. Finally, it took advantage of the unlabeled and annotated corpus to validate improved incremental algorithm of Naive Bayes. The experimental results show that an improved incremental algorithm of Naive Bayes significantly outperforms traditonal incremental algorithm.
Naive Bayes, incremental algorithm, feature space, evaluation index
TP181
A
10.11959/j.issn.1000-436x.2016199
2016-05-11;
2016-08-01

曾谁飞(1978-),男,江西广昌人,北京邮电大学博士生,主要研究方向为智能信息处理、机器学习、深度学习和神经网络等。

张笑燕(1973-),女,山东烟台人,博士,北京邮电大学教授,主要研究方向为软件工程理论、移动互联网软件、ad hoc和无线传感器网络。

杜晓峰(1973-),男,陕西韩城人,北京邮电大学讲师,主要研究方向为云计算与大数据分析。
陆天波(1977-),男,贵州毕节人,博士,北京邮电大学副教授,主要研究方向为网络与信息安全、安全软件工程和P2P计算。
