面向云存储容错系统的RS再生码

2016-11-24鄢喜爱张大方杨金民张波云

通信学报 2016年10期

关键词：云存储

鄢喜爱，张大方，杨金民，张波云

（1. 湖南大学信息科学与工程学院，湖南长沙 410082；2. 湖南警察学院信息技术系，湖南长沙 410138）

面向云存储容错系统的RS再生码

鄢喜爱1,2，张大方1，杨金民1，张波云2

（1. 湖南大学信息科学与工程学院，湖南长沙 410082；2. 湖南警察学院信息技术系，湖南长沙 410138）

面向云存储容错系统提出了一种RS再生纠删码，该编码继承了RS编码容多错的可靠性，又能实现容三错的高效性。对RS再生码中单节点故障混合修复方法进行了介绍，并求出了混合修复时磁盘读取数的理论下界。从理论上对RS再生码的存储开销、译码效率、修复带宽进行了性能评估。实验结果表明，RS再生纠删码比同类纠删码的修复性能有较大的提升，特别是采用混合修复算法以后，系统单故障恢复时间下降20.8%～28.2%。关键词：云存储；容错；纠删码；RS码；RDP码

1 引言

在云存储系统中，数据中心一般由非常多的数据节点组成，存储的数据达EB级甚至ZB级，数据失效已成为一种常态，构建云存储系统必须考虑容错机制。存储容错通常采取复制和纠删码2种方法。复制方法操作简单，故障恢复快，但存储开销成倍增长，并存在副本一致性维护难的问题；纠删码在故障恢复时会消耗更多的网络带宽，但在容错能力和存储空间上占有绝对优势[1,2]。由于云平台上存储的数据呈指数级增长，云存储系统的容错方法逐渐从复制向纠删码转换。

纠删码可分为阵列码和 RS（Reed-Solomon）编码两大类。阵列码只有简单的异或运算，运算速度快，但一般只能容单错或双错。常用的阵列码有EVENODD码、RDP码和X-Code码等[3～5]。RS编码是可以容多错的编码，并且具备MDS（maximum distance separable）性质，常用于对存储要求较高的存储系统中。目前一些主流的云平台（Microsoft Azure、Google、HDFS等）逐步采用了RS编码。

标准 RS编码建立在二元有限域G(2ω)上。在G(2ω)中，加法的运算只需利用简单的XOR实现；乘法的运算较为复杂，若ω很小，可通过查询对数表和反对数表获得，否则，必须通过反复的迭代计算才能获得[6]。对RS编码的性能优化主要体现在解决有限域上乘法计算难的问题，主要的相关工作如下。BURGISSER等[7]提出借助拉格朗日插值方法可使RS的运算复杂度大大降低，但限制了纠删码的长度，并且当数据量增大时，时间消耗量仍然很大。LACAN等[8]提出用2个Vandermonde矩阵来构造编码，比一个Vandermonde矩阵加一个单位矩阵的构造效率要高。Plank等[9]提出将Vandermonde矩阵变成Cauchy矩阵，将整个RS编码的运算全部转化为XOR运算，但编译码的时间复杂度仍是平方级，分别为 O(nlogn)和 O(n2)。KALCHER S等[10]针对 RS编码提出一个基于矢量的多项式乘法的实现算法，并采用GPU进行加速。KHANO 等[11]通过旋转和移位来降低RS编译码的复杂度，但更新和重构的效率都有不同程度的降低。李小兵等[12]提出了RS编码与X-code编码相结合生成再生码，在双错情况下采用X-code编码，有效地提高了修复效率，但X-code编码可扩展性不好，重构时必须按照一定的顺序进行迭代，不方便进行并行操作。

云存储属于归档式存储，对系统的容错能力、编译码效率、重构效率都有较高的要求。针对有中心的云存储系统，本文设计了一种 RS码与扩展RDP（ERDP）码相结合的RS再生纠删码。再生码兼顾了RS码与阵列码的优良特性，当节点故障在三错以上仍采用容错能力强的RS编码进行修复，当节点故障在三错以下，启用只有 XOR运算的ERDP编码进行修复；因单节点故障是云存储系统中的主要故障类型，本文讨论了RS再生纠删码中单节点故障的磁盘读取方法，求出了磁盘读取数的理论下界。从理论上对RS再生纠删码的存储开销、译码效率、修复带宽进行了分析，最后通过实验对系统性能进行了评估。

2 RS再生纠删码

2.1 RS编码

RS编码时，将每个存储节点被分为 t个存储单元，每个存储节点的字长是ωbit，假设数据盘有n个，分别{D1,D2,…,Dn}，校验盘有 m 个，分别为{C1,C2,…,Cm}，校验盘存储单元的数据的生成函数为F。

RS校验编码的生成矩阵一般采用 Vandermonde矩阵[13]，定义F为m×n的Vandermonde矩阵，其中，fi,j=ji−1，则编码的生成可转化为以下形式。

图1是当n=6，m=3时RS编码的生成框架。

图1RS编码生成框架（n=6, m=3）

2.2 标准RDP编码

标准 RDP编码是一种容双错横式阵列码，所有编码存放在一个(p−1)×(p+1)的阵列中，其中，p为大于2的素数，前p−1列存放的是原始数据块，后2列存放的是冗余校验数据[14]。RDP编码的生成公式如式(1)和式(2)所示，其中，式(1)生成的是行校验码，式(2)生成的是正对角线校验码。

ci,j表示第 i行第 j列数据位的值，式(2)中＜i−j＞p表示(i−j)mod p 。

图2是当p=5时，标准RDP编码的形成过程描述。

图2RDP码的形成过程描述（p=5）

2.3 RS再生码（RS-ERDP）构造

2.3.1 有限域上的计算加速处理

设F(x)=fxm+fxm−1+…+fx1+f 为不可

m m−110

约多项式，G(2ω)上 2个元素 A和 B可表示为：A(x)=am−1xm−1+…+a1x1+a0和B( x)=bm−1xm−1+…+b x1+b，其中，(f f…f )、(aa…

10mm−10m−1m−2

a1a0)、(bm−1bm−2…b1b0)的取值范围为{0,1}，则A( x)和B( x)在G(2ω)上乘积可表示为

对于不可约多项式有

根据式(4)和有限域上交换律，式(3)可改写为

将式(5)改写为矩阵形式

若用A(i)表示矩阵的列向量，则

根据式(6)和式(7)，对于矩阵 C的第 k行，当i≥ 1时，可得

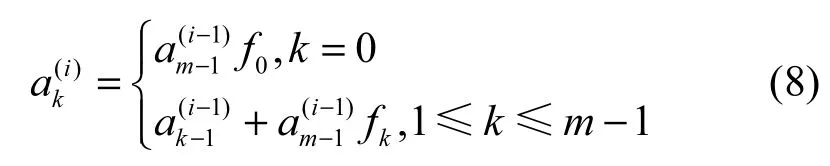
式(8)可进一步简化为

从式(9)可知，矩阵的第一列是(a0a1…am−1)，随后每一列是前一列左移一位，若前一列高位有溢出，则与(f0f1…fm−1)进行XOR运算。

根据以上的推导，有限域上的乘法就可演化为只含移位和XOR运算的计算，计算复杂度明显降低。后续标准的 RS编码和译码计算将按此方法处理。如在G(24)中，A=5，B=12，设定不可约多项式为F( x)=x4+x+1，则乘积C可通过下面方法获得。

A(0)=5=(a3a2a1a0)=(0101)2，=0，只需将A(0)左移1位，得A(1)=(1010)2；=1，将A(1)左移1位，再与(f0f1…fm−1)进行异或运算，A(2)=10100⊕10011=0111；因为=0，只需将A(2)左移1位，得A(3)=1110。计算结果与查询对数表和反对数表一致。

2.3.2 扩展RDP编码

为了增加 RDP编码的容错能力，本文构建了一种可扩展 RDP编码（ERDP）。编码过程中，增加一个校验节点，所有编码存放在一个(p−1)×(p+2)的阵列中，p为大于2的素数，前p−1列存放的是原始数据块，后3列存放的是冗余校验数据。在后3列中，前2列存放的编码与标准RDP的校验码一样，最后一列存放的编码为反对角线校验码，通过式(10)生成。

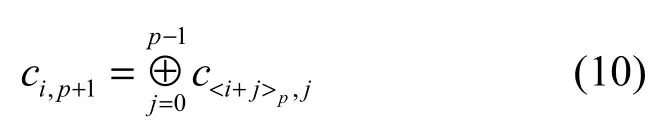
ci,j表示第i行第j列数据位的值，＜i+j ＞p表示(i+j)mod p 。

图3是当p=5时，ERDP编码的形成过程描述。

ERDP编码是一个可容三错的横式阵列码，在单错或双错情况下，解码方法与标准 RDP码完全相同，当出现三错时，启用反对角线校验码。假设3个失效盘为Dx、Dy、Dz，3个修复的校验算子分别为

图3ERDP码的形成过程描述（p=5）

2.3.3 RS再生码的生成

结合RS编码与ERDP编码的特性，本文构造了一种RS-ERDP的容错纠删码。为了能容忍多错，内部编码仍采用标准RS编码，为了达到3个错误以内高效地修复，外部采用只含 XOR运算的 RS再生码，即外部采用在 RS编码基础上生成的ERDP编码。由于RDP编码对磁盘数提出了要求（p为素数），为了不破坏RS编码对磁盘数无要求的优良特性，在生成RS编码之后，先分组再生成ERDP编码。

假设RS编码中数据盘数为n，RS编码校验盘数为m，ERDP编码磁盘数为p+2，RS-ERDP编码的构造步骤如下。

表1一个RS单元的ERDP编码生成过程

Step1将文件按条带分成 n块，利用Vandermonde矩阵生成RS编码，一个条带中会存在m+n个编码块。

Step2将条带分组，每组编码块的个数为p−1(p 为素数)，

Step3每组增加3个容错节点，将每一组的原RS编码生成ERDP编码。其中，p列存放行校验码，p+1列存放正对角线校验码，p+2列存放反对角线校验码。

表 1是 n=3，m=3，p=7时，一个 RS单元的ERDP编码生成情况。原始数据块存储在D0、D1、D2列，RS编码存储在D3、D4、D5列，ERDP编码存储在D6、D7、D8列。

3 RS-ERDP编码中单节点故障修复的读盘优化

在云存储系统中，单节点故障发生的概率占90%以上。一旦出现第1个失效节点，其他节点失效的概率会大大增加，更多节点失效会随后发生[15]。因此，当系统中出现单节点失效时，需要尽快修复至正常状态。影响单节点修复的关键因素是磁盘的读取，读取的磁盘数越少，则修复越快。如果失效节点是校验节点，因为生成校验时最多只参与了一次，所以只能重新生成编码，磁盘的读取没有优化空间；如果失效节点是数据节点，因为生成校验时可能参与了多次，所以磁盘的读取可以进行优化。

在 RDP编码中，传统的节点故障修复的方法是通过单一的行校验来进行修复，即读取行校验节点和存储节点的所有数据，数据节点的读取次数为(p−1)2。传统的修复方法忽视了对角线校验的存在，行校验与对角线校验会存在一些公共数据节点（同时参与了行校验与对角线校验）。对于公共数据节点，如果采用行校验和对角线校验进行混合修复，节点只需读一次就可以了，这样可以有效降低磁盘的读取次数。XIANG等[16]提出了一种容双错RDP编码中单节点故障的混合修复方法，行校验和对角线校验修复各取一半，得出数据节点的读取次数的理论下界为

在 RS-ERDP编码中，增加了一个反对角线校验，存在的公共数据节点会更多。下面本文来探讨容三错 RS-ERDP编码中单节点故障修复的读盘优化问题。

定义1

1) 设行校验集合为

2) 设对角线校验集合D为

3) 设反对角线校验集合B为

从定义可知|R|=|D|=|B|=p−1。

引理1

证明1) 根据定义1可知，当r=(i−j)mod p时，若0≤r≤p−2，有di,＜i−j＞p∈Ri若i+r≡i+(i−j)=j(modp)，有di,＜i−j＞p∈Dj，从而可推导di,＜i−j＞p∈Ri∩Dj，也即Ri∩Dj≠∅；由于 p是素数，有且仅有，即

2) 证明方法同1)。

假设在进行单节点修复时，选用3种校验方案进行混合修复，假设有λ个行校验组，ρ个对角线校验组，γ个反对角线校验组。又假设行校验组与对角线校验组公共节点数为SRD，行校验组与反对角线校验组公共节点数为SRB，对角线校验组与反对角线校验组公共节点数为SDB，总公共节点数为S。根据引理1，有

结合式(14)、式(15)有

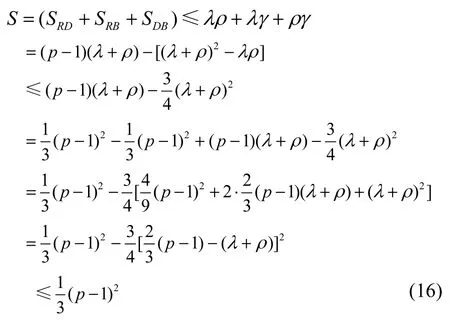
总公共节点数的理论上界为1(p−1)2设混合3，修复时节点读取数为W，单一修复数据节点的读取次数为(p−1)2，则W的理论下界为

由式(17)可知，当采用行校验、对角线校验、反对角线校验三者进行混合修复时，且3组的取值相近会逼近最少的磁盘读取数

4 RS-ERDP编码的性能分析

4.1 存储开销

假设原文件大小为1 MB，容错时若采用目前常用的3副本完全复制容错方式，则存储空间占用3 MB；若采用RS编码方式，每个编码块的大小为，则存储空间占用

若假设原文件大小为50 MB，3副本完全复制、RS编码、RS-ERDP编码3种容错的存储开销比较如图4所示。从图4(a)可看出，当p值固定，且m不变时，RS编码、RS-ERDP编码的存储开销都随着n的增大而降低，S趋向于；从图 4(b)可看出，当（n,m）固定时，RS-ERDP编码的存储开销随着 p的增大而降低，S趋向于

4.2 译码效率

为了便于比较，定义每个数据块的大小为1 bit，译码效率每个数据源信息块的平均异或次数（修复失效数据总异或次数与源数据比特数之比）。对容三错的RS-ERDP编码、RS编码、EVENODD编码的译码性能进行比较。

由文献[5]得知，容三错EVENODD编码异或的总次数为(4ld−2+3p)(p−1)−3。由文献[17]得知，基于XOR的RS编码异或的总次数约为krL2，k表示码的信息位，r表示冗余校验位长度，L表示有限域的大小，为了便于比较，取相同的冗余校验位r=3。

在容三错RS-ERDP编码中，根据式(11)～式(13)容易得知，3个校验算子总异或次数之和为3p2−11p+6，将校验算子作为方程组，通过消元计算出恢复三错中一个失效列总异或次数之和为3(ld−1)(p−1)+(p−2)，剩余两错按常规的RDP容双错处理，总异或次数之和为4(p−2)−1[18]，RS-ERDP译码总异或次数为上述3部分之和。

图4存储开销对比

数据源比特数为2(p−1)，RS-ERDP码、RS码、EVENODD码的译码效率如图5所示。

图5译码效率比较

从图 5可看出，当节点数量少（p＜11）时，RS-ERDP码的译码效率在略高于EVENODD码，但当节点数增长（p＞11）时，RS-ERDP码的平均异或次数较EVENODD码增长更缓慢，而且译码效率要高。RS码的译码效率最低，主要与有限域的大小相关，并且随着域的扩大而增加。

4.3 单节点故障修复带宽

假设每个编码块的大小为1 MB，在RS码中，根据RS（n,m）思想[19]，恢复一个失效数据块，需要获取n个数据块，一个节点含有p−1个数据块，所以期间若单节点发生故障其修复带宽为(p−1)nMB ，对于传统RDP码单故障修复带宽视p的大小决定，在RS-ERDP码单故障修复时，本文采用混合修复的方法，由于行、对角线、反对角线存在公共节点，修复带宽可进一步减少。RS码、RDP码、RS-ERDP码单节点故障修复带宽如表 2所示。RS-ERDP码只是局部单元修复组修复，一般p＜n，所以RS-ERDP修复带宽最低。

表2单节点故障修复带宽比较

5 基于RS-ERDP编码的云存储容错架构

基于 RS-ERDP编码的有中心云存储容错架构如图 6所示。存储客户端将待存储的文件生成RS-ERDP编码发至云端文件服务器。文件服务器包括元数据信息管理模块和心跳感知模块。元数据信息管理模块负责处理编码块的名字空间、索引记录、编码块到存储节点映射等方面的信息。心跳感知模块通过心跳感知存储节点是否发生故障，并根据故障节点数来决定采用RS编码还是RS-ERDP编码，并将相关信息反馈给元数据信息管理模块。心跳感知模块执行编码选择的方案如表3所示。文件读取时，客户端首先从服务器获取文件编码块的偏移信息，再从存储集群节点中读取，读取分为正常读取和故障读取2种方式。

表3编码选择方案

图6基于RS-ERDP编码的云存储容错架构

文件服务器是系统架构的核心部分，为增强其可靠性，本文采用双机热备的方式进行工作。两台同构的服务器同时加电工作，一个任务同时发送到主从服务器。正常情况下从服务器不指挥工作，当主服务器发生物理故障时才接管指挥工作。主从服务器周期性地做检查点并比较检查点结果（状态）是否相同，若相同，说明系统正常，若不相同，判定其中一台服务器发生软故障，主从服务器同时回卷到上一个检查点状态，重新执行工作。

6 实验性能评估

6.1 实验环境

本实验在开源的分布式存储系统NCFS中进行[20]。NCFS连接各存储设备,并根据配置的不同编码机制将数据分块并按照条带编码分散存储在相关的存储设备中。

实验的硬件环境如表4所示。

表4实验环境的硬件配置

6.2 节点故障修复时间比较

为了比较不同编码的修复性能，本文在 NCFS存储系统中分别实现了 RS码、RS-cauchy码、RS-ERDP码，为了便于比较，还构建了容三错的RS-EVENODD码。节点失效利用断电的方式离线处理。实验中通过调整p值的大小来比较系统的整体修复时间（下载数据时间、修复时间、写数据时间）。实验测试了不同编码在参数 p值不同的情况下的修复性能。实验结果如图7所示。

实验结果表明，在容三错的范围内，由于全部采用只含XOR运算的阵列码来容错，RS-ERDP码的恢复性能较 RS编码、RS-cauchy都有明显的提升，而且随着存储节点、故障节点的增多，优化性能越明显。此外，随着存储规模地增大，RS-ERDP码的修复性能变化平缓，非常适合于大规模的云存储容错。RS-ERDP码与RS-EVENODD码的比较结果是：节点数量小（p＜11）时，RS-ERDP码性能略低；当节点数量增多（p＞11）时，RS-ERDP码性能要高于RS-EVENODD码。这是由于RS-ERDP编码多一列参与对角线校验，节点数量少时，每比特译码的平均XOR次数略高于RS-EVENODD码，当节点数增多时，每比特译码的平均XOR次数会低于RS-EVENODD码，并且RDP的小写性能和数据读取平衡性优于EVENODD。

图7不同节点数情况下各类编码的恢复性能比较

6.3 单节点故障修复性能比较

针对于单节点故障修复，本文对传统的修复与混合修复进行了比较。实验测试了 RS-ERDP编码在参数p不同的情况下的修复性能。实验中数据块大小分别取值为 1024 KB、2048 KB，p∈{5,7,13,17,19,23}，传统修复只采用行校验，混合修复采用行校验、对角线校验、反对角线校验三者混合修复，且3组取值接近，实验结果如图8所示。

图8传统修复与混合修复在不同节点个数情况下的性能对比

柱状图顶端的数字表示优化百分比。实验结果表明，当数据块的大小为1024 KB时，数据修复时间减少20.8%～26.6%，当数据块的大小为2048 KB时，数据修复时间减少25.8%～28.2%；从变化趋势可看出，节点个数越多，优化效果越好，这是由于存在更多公共数据块的原因。理论的下界是减少33.3%，优化的结果离理论下界还有一定的差距，这是由于混合修复时磁头不是连续读，在寻道上有一定的延时。

7 结束语

云存储是大规模的海量存储，必须具有可靠而又高效的容错特性。本文设计了兼备RS码与阵列码优良特性的 RS-ERDP容错纠删码，当发生多个节点故障时可启用内部RS编码进行修复，当节点故障在3个以下时可启用只含XOR运算的ERDP码，并讨论了容三错ERDP码中单节点故障的磁盘读取问题，通过混合修复降低了磁盘读取数，求出了三容错中磁盘读取的理论下界。从理论和实验 2个方面对编码的容错性能维护开销进行了分析，结果表明 RS-ERDP容错纠删码通过少量的额外存储代价可获得准确高效的数据修复效果，适应于对实时性、可靠性要求较高的云存储系统。

[1]王意洁, 孙伟东, 周松, 等. 云计算环境下的分布存储关键技术[J].软件学报, 2012, 23(4): 962-986 WANG Y J, SUN W D, ZHOU S, et al. Key technologies of distributed storage for cloud computing[J]. Journal of Software, 2012, 23(4):962-986.

[2]谭鹏许, 陈越, 兰巨龙, 等. 用于云存储的安全容错编码[J]. 通信学报, 2014, 35(3): 109-115.TAN P X, CHEN Y, LAN J L, et al. Secure fault-tolerant code for cloud storage[J]. Journal on Communications, 2014, 35(3): 109-115.

[3]LUO J Q, MOCHAN S, XU L H, et al. Efficient encoding schedules for XOR-based erasure codes[J]. IEEE Transactions on Computers,2014, 63(9): 2259-2272.

[4]LI M, SHU J. On cyclic lowest density MDS array codes constructed using starters[J]. IEEE International Symposium on Information Theory, 2010, 41(3): 1315-1319.

[5]万武南, 吴震, 陈运, 等. 一种基于3容错阵列码的RAID数据布局[J]. 计算机学报, 2007, 30(10): 1722-1730.WAN W N, WU Z, CHEN Y, et al. A data placement based on toleration on triple failures array codes in RAID[J]. Chinese Journal of Computers, 2007, 30(10): 1722-1730.

[6]KVASHENNIKOV V V. Application of fast polynoamial transformations over GALOIS GF(2m) fields in Reed-Solomon coding and decoding[J]. Telecommunications and Radio Engineering, 2012, 71(10):85-90.

[7]BURGISSER P, CLAUSEN M, SHOKROLLAHI MA. Algebraic complexity theory[M]. Springer Verlag Heidelberg. 1996.

[8]LACAN J, FIMES J. Systematic MDS erasure codes based on Vandermonde matrices[J]. IEEE Communications Letters, 2004, 8(9):570-582.

[9]PLANK J S, XU L.Optimizing cauchy Reed-Solomon codes for fault-tolerant network storage applications [C]//The 5th IEEE International Symposium on Network Computing and Applications (IEEE NCA06). Cambridge, MA, 2006: 1-8.

[10]KALCHER S, LINDENSTRUTH V. Accelerating Galois field arithmetic for Reed-Solomon erasure codes in storage applications[C]//IEEE International Conference on Cluster Computing. 2011: 290-298.

[11]KHAN O, BURNS R, PLANK J S. Rethinking erasure codes for cloud file systems: minimizing I/O for recovery and degraded reads[C]//USENIX. FAST 2012: 10th USENIX Conference on File and Storage Technologies. San Jose, CA, 2012: 1-14.

[12]李小兵, 许胤龙, 林一施, 等. 再生码:一类适用于云存储的准确修复编码[J]. 计算机应用与软件, 2014, 31(8): 241-244.LI X B, XU Y L, LIN Y S, et al. X regenerating codes: a class of accurate repair codes for cloud storage [J]. Computer Applications and Software, 2014, 31(8): 241-244.

[13]PLANK J S. A tutorial on Reed-Solomon coding for fault-tolerance in RAID-like systems[J]. Software: Practice and Experience, 1997, 27(9):995-1012.

[14]CORBETT P, ENGLISH B, GOEL A, et al. Row diagonal parity for double disk failure correction [C]//Proceedings of the Third USENIX Conference on File and Storage Technologies. Berkeley, CA, USA,2004: 1-14.

[15]邱丽娜, 王芳, 李楚, 等. 一种容三盘失效纠删码的单数据盘失效快速重建方法[J]. 计算机学报, 2013, 36(10): 2041-2051.QIU L N, WANG F, LI C, et al．EDS: a novel scheme for boosting single disk failure recovery of triple erasure correcting code storage systems[J]. Chinese Journal of Computers, 2013, 36(10): 2041-2051.

[16]XIANG L，XU Y, LUI J C S, et al. Optimal recovery of single disk failure in RDP code storage systems[J]. ACM Sigmetrics Performance Evaluation Review[J]. ACM, 2010, 38(1): 119-130.

[17]BLOEMER J M, KALFANE M, KARPINSKI R. An XOR-based erasure-resilient coding scheme[R]. Technical Report at ICSI, 1995.

[18]万武南, 王拓, 索望. 一种三容错数据布局[J]. 电子与信息学报,2013, 35(10): 2341-2346.WAN W N, WANG T, SUO W, et al. A data placement based on toleration triple failures[J]. Journal of Electronics amp; Information Technology, 2013, 35(10): 2341-2346.

[19]LI J, LI B. Erasure coding for cloud storage systems: a survey[J].Tsinghua Science and Technology, 2013, 18(3): 259-272.

[20]HU Y, YU M C, LEE P P C, et al. NCFS: on the praticatity and extensibility of a network-coding based distributed file system[C]// International Symposium on Network Coding. Beijing, 2011: 1-6.

RS regenerating codes for cloud storage fault-tolerant system

YAN Xi-ai1,2, ZHANG Da-fang1, YANG Jin-min1,ZHANG Bo-yun2
(1. College of Computer Science and Electronic Engineering, Hunan University, Changsha 410082, China;2. Department of Information Technology,Hunan Police Academy, Changsha 410138, China)

RS(Reed-Solomon) regenerating erasure codes was proposed for cloud storage fault-tolerant system, which not only inherited the reliability of the RS encoding, but also achieved the high efficiency of tolerance three faults. Hybrid recovery method of the single fault node based on RS regenerating erasure codes was introduced. And the theoretical lower bound of the number of accessing disks was computed. In theory, the performance evaluation of the storage overhead, decoding efficiency, and repair bandwidth of the RS regenerating erasure codes was carried out. Experiments results show that the repair performance of RS regenerating erasure codes is improved greatly than the similar erasure codes, and the total recovery time of the system is reduced by 20.8%～28.2% using hybrid recovery algorithm in the case of single fault.

cloud storage, fault tolerance, erasure codes, RS encoding, RDP encoding

s:The National Natural Science Foundation of China(No.61472130，No. 61471169), The National Key Basic Research and Development Program of China (973 Program) (No.2012CB315805), Ministry of Public Security Public Security Theory and Soft Science Research Projects (No.2013LLYJHNST040), Hunan Provincial Science and Technology Department Research Projects(No.2014FJ3049), Hunan Provincial Key Laboratory of Network Investigational Technology Research Projects (No. 2016WLZC006)

TP391

10.11959/j.issn.1000-436x.2016197

2016-02-22；

2016-05-23

国家自然科学基金资助项目（No.61472130，No.61471169）；国家重点基础研究发展计划（“973”计划）基金资助项目（No. 2012CB315805）；公安部公安理论及软科学研究计划基金资助项目（No.2013LLYJHNST040）；湖南省科技厅科研基金资助项目（No. 2014FJ3049）；网络侦查技术湖南省重点实验室基金资助项目（No. 2016WLZC006）