均匀散射环境中物理层安全密钥容量分析
2016-11-24王旭金梁刘璐李明亮黄开枝
王旭,金梁,刘璐,李明亮,黄开枝
(国家数字交换系统工程技术研究中心,河南 郑州 450002)
均匀散射环境中物理层安全密钥容量分析
王旭,金梁,刘璐,李明亮,黄开枝
(国家数字交换系统工程技术研究中心,河南 郑州 450002)
物理层安全密钥容量受信道测量时差、终端移动和加性噪声等因素影响,在均匀散射环境中定量分析了上述因素对密钥容量的影响。在分析含噪窄带信道参数的时域统计特性的基础之上,推导了密钥容量时域闭式解,并且分别在均匀散射和非均匀散射环境中验证了推导结果的正确性和适用性。
物理层安全;物理层安全密钥;密钥容量;均匀散射环境
1 引言
随着移动通信应用领域的拓展,安全问题逐渐成为制约其发展的主要瓶颈之一。现有移动通信安全依靠高层密钥加密机制,但是在资源受限的新兴网络(如物联网等)中,高层密钥的分发和管理存在一定的安全隐患。而无线信道具有天然的密钥特征,通信双方通过测量同一无线信道提取相同的物理层安全密钥,可用于密钥分发并辅助高层密钥加密机制实现安全增强。现有物理层安全密钥研究[1,2]主要分为密钥提取技术[3~8]和密钥容量分析[9~11]。其中,密钥容量分析为密钥提取技术提供理论上界,具有重要理论研究价值。
Maurer[9]和 Csiszár[10,11]首先提出利用无线信道作为共享随机源提取密钥,并分析了密钥容量问题。物理层安全密钥提取的前提是无线信道的互易性,当通信双方同时测量同一无噪信道时,能够得到完全相同的信道参数,此时密钥容量无限大。但是大量文献研究表明,信道测量时差、终端移动以及热噪声等因素破坏了信道互易条件,限制了密钥容量。Patwari[12]指出实际系统中信道测量时差破坏了互易条件。为了降低信道测量时差对物理层安全密钥提取的影响,Shehadeh[13]利用一段时间内多次信道采样的平均值增加信道信息的一致性。与此同时,Shehadeh[13,14]指出终端移动带来的信道快变丰富了信道参数的随机性。除此之外,Nitinawarat[15]和Chou[4]等指出加性噪声对互易条件的破坏作用也不容忽视,并定量分析了加性噪声对密钥容量的影响。上述文献只考虑某一因素对密钥容量的影响,而 Wu[16]在均匀散射环境[17]中,综合考虑终端移动和加性噪声2个因素对密钥容量的影响,并给出了密钥容量的频域表达式。但是现有文献均只从部分因素入手分析密钥容量,未综合考虑信道测量时差、终端移动和加性噪声对密钥容量的影响。
针对上述问题,本文基于Csiszár[10]提出的Model S(source-type model),在均匀散射环境中定量分析了上述3个因素对密钥容量的影响。首先介绍均匀散射环境,分析了含噪窄带信道参数的时域统计特性;随后将密钥容量计算转化为随机变量的互信息计算问题,推导出密钥容量时域闭式解;在均匀散射环境中验证推导结果的正确性,并且仿真验证该结论在非均匀散射环境中同样适用。仿真结果表明,在具有大量散射体的环境中利用无线信道参数提取物理层安全密钥是可行的。该结论能够分析在密集散射场景中提取物理层安全密钥时的密钥容量。
2 系统模型
考虑一个具有丰富散射体的NLOS(无直达径)移动通信场景,单天线的基站Alice和移动终端Bob之间存在大量散射物。Bob从A点出发,按照移动速度v向B点方向移动。设Alice到Bob之间的无线信道为下行信道,Bob到Alice的信道为上行信道;同时,假设系统中存在单天线被动窃听者Eve,即Eve可以被动接收信号但是不能够发送信号干扰信息传输。由于建筑物或者其他人为或者自然散射体的存在,导致通信双方之间的电磁波(工作在超高频或者更高频段)产生大量的散射、反射、折射和衍射。均匀散射模型[17,18]能够建模这一典型移动通信场景的无线信道参数,包括幅度、相位、空间相关性、频域相关性等特性。如图1所示,在该模型中散射体均匀分布在以终端为圆心的圆周上,以保证入射功率[18](incoming power)来自各个方向。该模型假设终端周围有N个散射体,第n(n≤N)个散射体到达终端的角度为nΔθ,其中,相邻2个入射径的夹角为,且假设从各个散射体到达终端的电磁波衰减相同。
根据文献[19],在t时刻,Alice和Bob之间的窄带无线信道h(t)可用其等效复基带表示
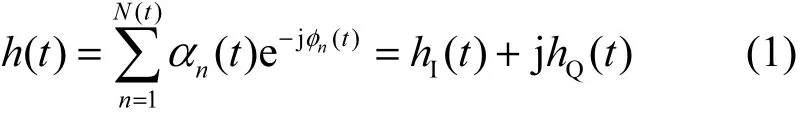
其中,hI(t)、hQ(t)表示信道参数的同相/正交(I/Q)分量;N(t)表示t时刻散射体数量;为信道衰减表示信道相位偏移。在均匀散射环境条件下与相互独立,由中心极限定理可得,当N(t)足够大时,h(t)服从零均值、方差为的高斯随机分布,即

图1 均匀散射环境
3 密钥容量分析
本文基于Model S[10]进行研究,将无线信道作为共享随机源,Alice和Bob通过测量获取具有一定相关性的信道信息。同时,Chen[20]指出当Eve到Alice和Bob距离大于几个波长时,可认为窃听信道(Eve与Alice和Eve与Bob之间的信道)与合法信道(Alice与Bob之间的信道)相互独立,此时Eve利用信道相关性窃取的密钥数可以忽略。因此,假设Eve与Alice和Bob距离均超过几个波长,此时可以利用Alice与Bob测量信道参数的互信息,代替存在Eve被动窃密时的条件互信息计算密钥容量[9,10]。本节首先分析均匀散射环境中含噪窄带信道参数的统计特性;随后推导利用信道参数提取密钥时,密钥容量的时域闭式解。
3.1 信道参数的统计特性
当Alice在t时刻对信道进行测量时,测得含噪
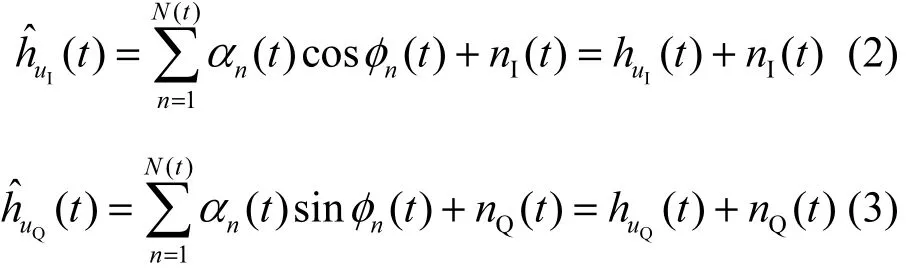
3.2 密钥容量时域闭式解
由3.1节分析可知,合法通信双方测量的信道参数是具有相关性的复高斯随机变量,下面对利用具有一定相关性的信道参数提取密钥时的密钥容量进行分析。由于I/Q分量地位等价且分析方法相同,因此,在不失一般性的情况下选用I分量对密钥容量进行分析。又密钥容量CS是双方测量信道参数的互信息,且高斯随机变量的互信息可通过相关系数表示[15,21]。所以,利用I分量提取的物理层安全密钥容量满足式(4)。

其中,ρ表示双方测量信道参数的相关系数。

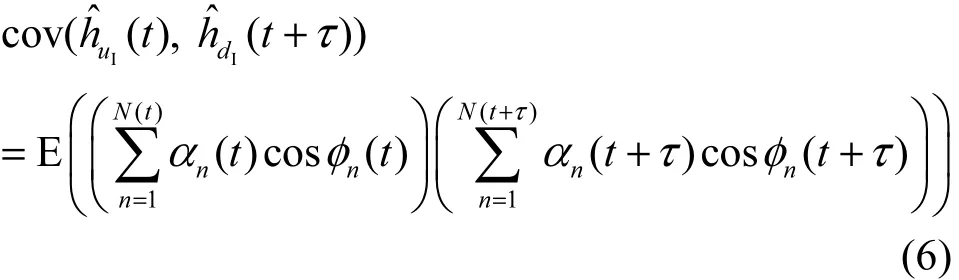
由于终端移动速度远小于光速,一次密钥提取过程中终端移动距离足够小,可认为在密钥提取时间内散射体数量、信道衰减、终端移动速度 v以及多普勒频移fDn保持不变。将(其中,τn为传播时延)代入式(6)得到式(7)。

又由于fcτn变化程度远大于fDnt和fDnτ,即τn变化很小就足以使接收信号的相位信息2π变化。故可认为在范围内为均匀分布,所以,进而有式(8)成立。
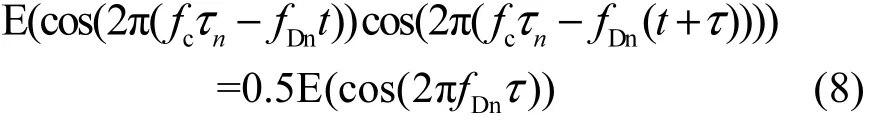
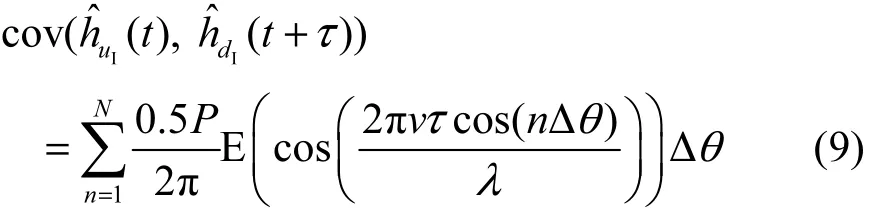
当N→+∞时,式(6)可进一步化简为
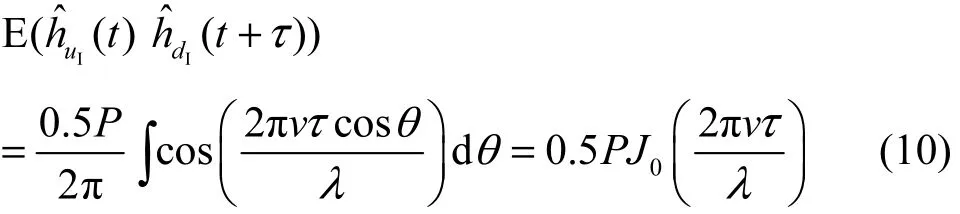



特别地,当vτ=0时

其中,

由上述分析可知,在均匀散射环境中窄带无线信道参数近似服从复高斯分布。且利用无线信道参数提取物理层安全密钥时,密钥容量可由信道测量时差、终端移动速度和信噪比定量表示。
4 仿真分析
仿真条件采用 Fontán[22]给出的典型均匀散射环境(如图2所示)的仿真条件;仿真方法采用文献[23~25]给出的 Copula熵估计算法,进行密钥容量估计;仿真数据通过105次独立的蒙特卡洛仿真实验得到。本节首先验证推导结果的正确性,并定量分析信道测量时差τ、终端移动速度v和SNR对密钥容量的影响;随后在非均匀散射环境中验证推导结果的适用性(适用性指式(13)对于均匀散射环境和非均匀散射环境均适用)。
4.1 正确性验证
在图2所示的均匀散射仿真环境中,通过105次蒙特卡洛实验得到仿真数据。仿真条件如下。
1) Bob的各角度入射功率相同,载波频率为2 GHz,且Alice和Bob之间没有直达径。
2) SNR∈[0, 20]dB 且 SNRA(t)= SNRB(t +τ)。
3) Bob沿着x轴正向移动,速度v∈[0, 200] m/s,信道测量时差 τ∈[0, 200] μs。
4) 每次仿真中Alice位置固定,1 000个散射点在以原点为圆心、半径为 200 m的圆周上按照[0,2π]的均匀分布随机产生。
仿真步骤如下。
1) 如图2所示,在以原点为圆心,200 m为半径的圆周上,按照[0, 2π]的均匀分布随机产生1 000个散射点。
2) 固定Alice位置在(−700, 700) m,在Bob以速度 v从原点沿着 x轴正向移动过程中,Alice和Bob分别在t和t+τ时刻测量无线信道,得到无线信道参数的一组仿真数据。
3) 重复步骤1)和步骤2) 105次,得到105组无线信道参数的仿真数据。
4) 利用仿真数据计算相关系数估计值,同时根据文献[25]处理仿真数据得到密钥容量估计值。

图2 均匀散射环境仿真示意
在图 2所示的均匀散射模型中进行仿真。图3(a)、图4(a)分别为τ=100μs条件下信道参数相关系数、密钥容量与移动速度和SNR关系;图3(b)、图4(b)为ν=100m/s条件下信道参数相关系数、密钥容量与测量时间差和SNR关系。
随着箭头指向,对应的6组曲线的SNR分别为 0 dB、5 dB、10 dB、15 dB、20 dB和+∞ dB(下同),图3中有噪理论值指式(11)计算的I(Q)分量的相关系数;I(Q)分量指在仿真条件下,利用仿真数据估计的I(Q)分量相关系数估计值。
图4中有噪理论值指式(12)计算的I(Q)分量的密钥容量理论值;I(Q)分量指在仿真条件下,利用仿真数据得到的I(Q)分量密钥容量的估计值。
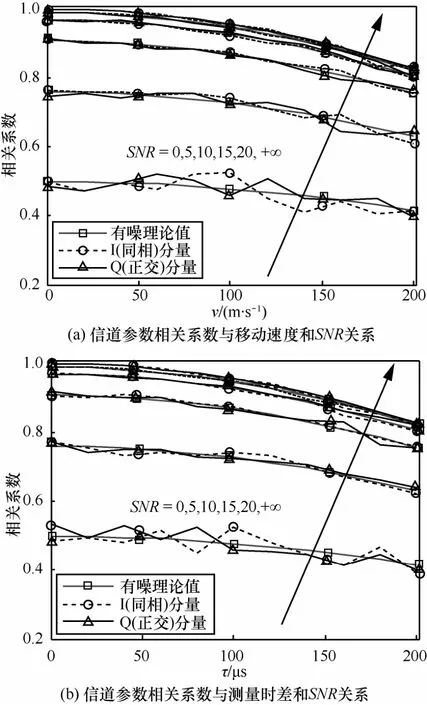
图3 均匀散射环境中信道参数相关系数变化曲线
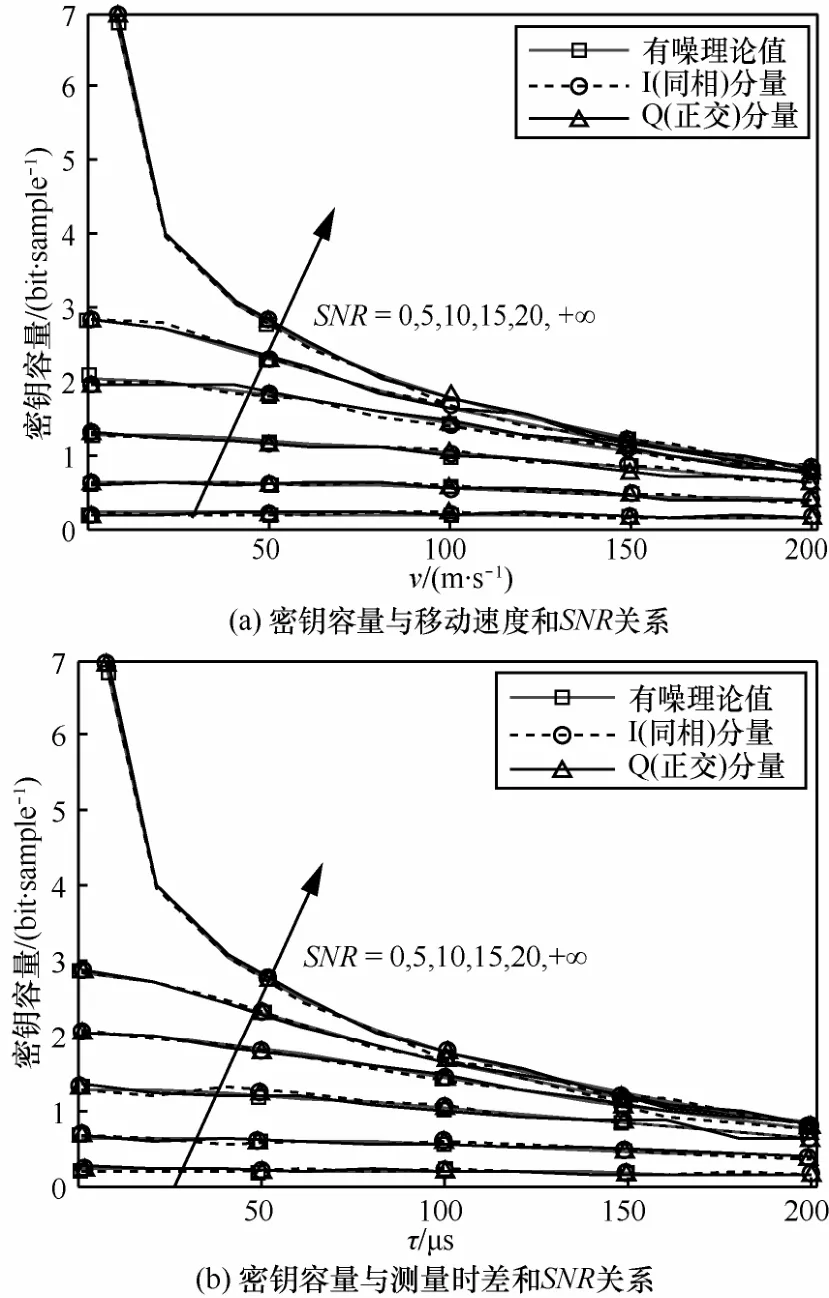
图4 均匀散射环境中密钥容量变化曲线
由图3可知,随着SNR的提高,信道参数的相关系数逐渐提高;且随着SNR的提高,利用仿真数据估计的相关系数与式(11)计算的理论值一致性逐渐增强。由图4可知,随着SNR提高,密钥容量逐渐提升。特别地,当SNR趋近于无穷大且Alice和Bob位置保持不动时,密钥容量趋于无穷大。
由图3和图4可得仿真估计值与式(11)和式(12)一致性较好,验证了推导结果的正确性。对比图3(a)和图3(b)、图4(a)和图4(b)可知,测量时间差τ与移动速度v对相关系数以及密钥容量的贡献相同。这是由于移动距离s=vτ,即v和τ共同作用,改变终端的空间位置,进而影响信道状态。
4.2 适用性验证
如图5所示,在非均匀散射环境中进行密钥容量估计,通过与式(12)计算的密钥容量理论值比较,论证推导结果的适用性。仿真结果通过105次蒙特卡洛实验得到,仿真条件如下。

图5 非均匀散射环境仿真示意
1) 电磁波衰减遵循自由空间路径损耗规律,每经历一个波长相位变化2π,Alice和Bob之间没有直达径,载波频率为2 GHz。
2) SNR∈[0, 20] dB,且 SNRA(t)= SNRB(t+ τ)。
3) Bob沿着x轴正向移动,速度v∈[0, 200] m/s,信道测量时差 τ∈[0, 200] μs。
4) 每次仿真中Alice位置固定,100个散射点在 x∈[-900, 200] m,y∈[−200, 900] m 内均匀产生。
仿真步骤如下。
1) 在x∈[-900, 200] m,y∈[-200, 900] m的矩形区域内,按照均匀分布产生100个散射点。
2) 固定Alice位置在(−700,700)m,在Bob以速度v从原点沿着x轴正向移动过程中,Alice和Bob分别在t和t+τ时刻测量无线信道,得到无线信道参数的一组仿真数据。
3) 重复步骤1)和步骤2) 105次,得到105组无线信道参数的仿真数据。
4) 利用仿真数据计算相关系数估计值,同时根据文献[25]得到密钥容量估计值。
图6(a)、图6(b)分别为在图5所示非均匀散射仿真环境中,当v=100m/s时,信道参数相关系数、密钥容量与信道测量时差和SNR关系。
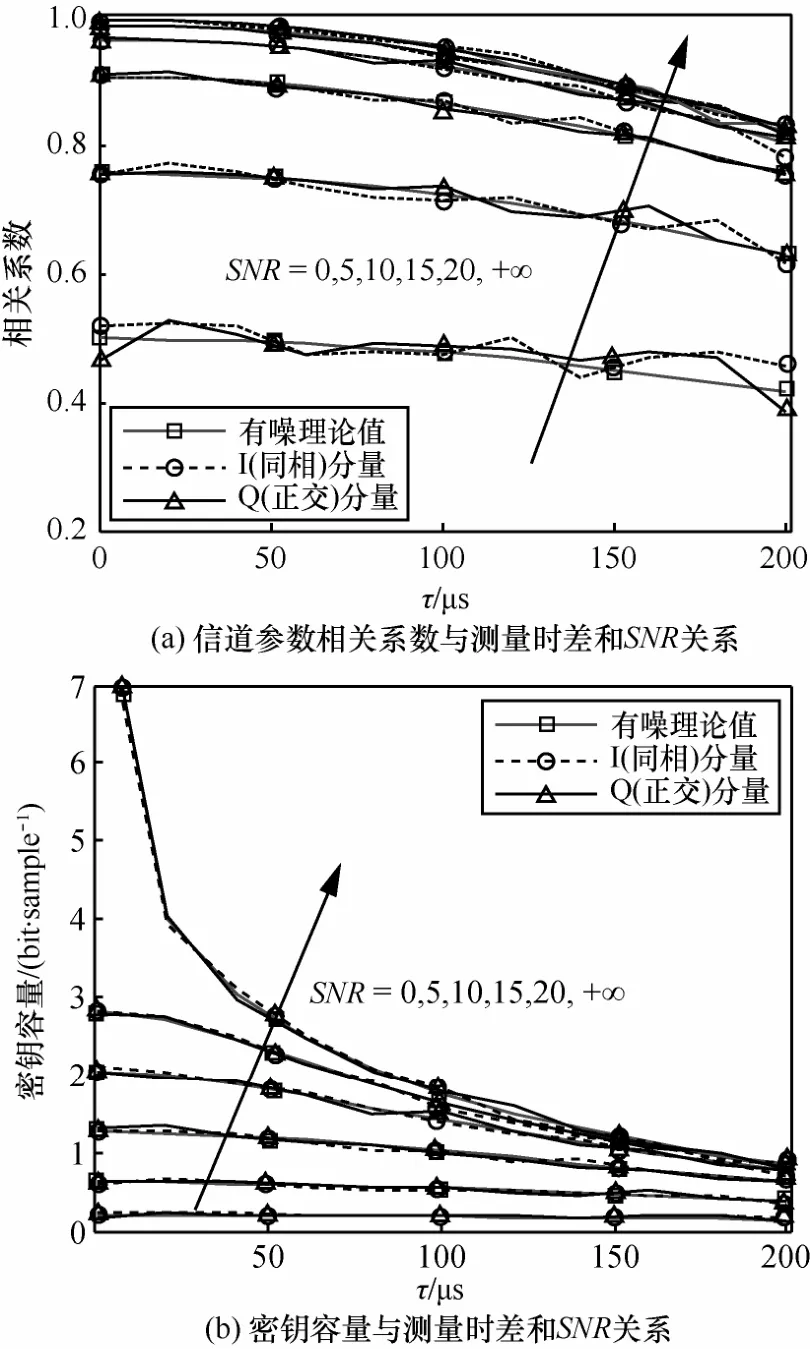
图6 非均匀散射环境中信道参数相关系数和密钥容量变化曲线
由图6可知,在图5所示的非均匀散射环境中,利用仿真数据估计的信道参数相关系数以及密钥容量,与分别利用式(11)和式(12)计算的信道参数相关系数和密钥容量较为吻合。这是由大数定理保证的,具体地,是因为密集分布的散射体能够保证Alice和Bob之间的信道参数仍可近似为复高斯分布。进而保证推导结果并不局限于均匀散射环境,对于存在大量散射体的非均匀散射环境依然适用。
综合4.1节和4.2节可知,利用式(13)能够分析在有大量散射体的环境中,利用无线信道参数提取物理层安全密钥时的密钥容量。
5 结束语
本文在均匀散射环境中,推导了利用无线信道参数提取物理层安全密钥时,密钥容量的时域闭式解,能够定量分析信道测量时差、终端移动和加性噪声对密钥容量的影响。本文首先分析了均匀散射环境中含噪信道参数的时域统计特性;随后将密钥容量计算问题转化为随机变量的互信息计算问题,推导了密钥容量时域闭式解;最后通过蒙特卡洛仿真,分别在均匀散射和非均匀散射环境中验证了推导结果的正确性和适用性。仿真结果表明,在有大量散射体的环境中,根据给定的信道测量时差、终端移动速度和信噪比可近似确定密钥容量。该结论可以为在散射丰富的移动通信环境中,提取物理层安全密钥提供理论参考。
[1] SHEHADEH Y E H, HOGREFE D. A survey on secret key generation mechanisms on the physical layer in wireless networks [J]. Security and Communication Networks, 2015, 8(2): 332-41.
[2] WANG T, LIU Y, VASILAKOS A V. Survey on channel reciprocity based key establishment techniques for wireless systems [J]. Wireless Networks, 2015, 21(6): 1835-46.
[3] THAI C D T, LEE J, QUEK T Q. Physical-layer secret key generation with colluding untrusted relays [J]. IEEE Transactions on Wireless Communications, 2016, 15(2): 1517-30.
[4] CHOU T H, DRAPER S C, SAYEED A M. Key generation using external source excitation: capacity, reliability, and secrecy exponent[J].IEEE Transactions on Information Theory, 2012, 58(4): 2455-74.
[5] PFENNIG S, FRANZ E, ENGELMANN S, et al. End-to-end key establishment with physical layer key generation and specific attacker models [M]. Physical and Data-Link Security Techniques for Future Communication Systems. Springer, 2016: 93-110.
[6] PREMNATH S N, JANA S, CROFT J, et al. Secret key extraction from wireless signal strength in real environments [J]. IEEE Transactions on Mobile Computing, 2013, 12(5): 917-30.
[7] TSOURI G R, WAGNER D M. Threshold constraints on symmetric key extraction from rician fading estimates [J]. IEEE Transactions on Mobile Computing, 2013, 12(12): 2496-506.
[8] 戴峤, 宋华伟, 金梁. 基于等效信道的物理层认证和密钥分发机制 [J].中国科学 信息科学, 2014, 44(12): 1580-92.DAI Q, SONG H W, JIN L, et al. Physical–layer authentication and key distribution mechanism based on equivalent channel[J]. Scientia Sinica Informationis, 2014, 44(12): 1580-1592.
[9] MAURER U M. Secret key agreement by public discussion from common information[J]. IEEE Transactions on Information Theory,1993, 39(3): 733-42.
[10] AHLSWEDE R, CSISZÁR I. Common randomness in information theory and cryptography. part I: secret sharing [J]. IEEE Transactions on Information Theory, 1993, 39(4): 1121-32.
[11] AHLSWEDE R, CSISZÁR I. Common randomness in information theory and cryptography part II: CR capacity [J]. IEEE Transactions on Information Theory, 1998, 44(1): 225-40.
[12] PATWARI N, CROFT J, JANA S, et al. High-rate uncorrelated bit extraction for shared secret key generation from channel measurements[J].IEEE Transactions on Mobile Computing, 2010, 9(1): 17-30.
[13] SHEHADEH Y E H, ALFANDI O, HOGREFE D. On improving the robustness of physical-layer key extraction mechanisms against delay and mobility[C]//IEEE Wireless Communications and Mobile Computing Conference. Limassol, Cyprus, 2012:1028-1033.
[14] SHEHADEH Y E H, ALFANDI O, HOGREFE D. Towards robust key extraction from multipath wireless channels [J]. Journal of Communications and Networks, 2012, 4(14): 385-95.
[15] NITINAWARAT S, NARAYAN P. Secret key generation for correlated Gaussian sources[J]. IEEE Transactions on Information Theory, 2012,58(6): 3373-3391.
[16] WU X, SONG Y, ZHAO C, et al. Secrecy extraction from correlated fading channels: an upper bound[C]//IEEE International Conference on Wireless Communications amp; Signal Processing. Nanjing, China, 2009.
[17] CLARKE R. A statistical theory of mobile‐radio reception [J]. Bell System Technical Journal, 1968, 47(6): 957-1000.
[18] JAKES W C, COX D C. Microwave mobile communications [M].New Jersey, USA: Wiley-IEEE Press, 1994.
[19] GOLD S A. Wireless communications[M]. Cambridge, UK: Cambridge University Press, 2005.
[20] CHEN C, JENSEN M. Secret key establishment using temporally and spatially correlated wireless channel coefficients[J]. IEEE Transactions on Mobile Computing, 2011, 10(2): 205-215.
[21] COVER T M, THOMAS J A. Elements of information theory [M].New Jersey, USA: John Wiley amp; Sons, 2012.
[22] FONTÁN F P, ESPIÑEIRA P M. Modelling the wireless propagation channel: a simulation approach with matlab [M]. New Jersey, USA:John Wiley amp; Sons, 2008.
[23] ZENG X, DURRANI T. Estimation of mutual information using copula density function [J]. Electronics Letters, 2011, 47(8): 493-494.
[24] MA J, SUN Z. Mutual information is copula entropy [J]. Tsinghua Science amp; Technology, 2011, 16(1): 51-4.
[25] 韩敏, 刘晓欣. 基于Copula熵的互信息估计方法[J]. 控制理论与应用, 2013, 30(7): 875-879.HAN M,LIU X X. Mutual information estimation based on copula entropy[J]. Control Theory amp; Applications, 2013, 30(7): 875-879.
Analysis of physical layer secret key capacity in the uniform scattering environment
WANG Xu, JIN Liang, LIU Lu, LI Ming-liang, HUANG Kai-zhi
(National Digital Switching System Engineering amp; Technological Research Center, Zhengzhou 450002, China)
Physical layer secret key capacity was affected by time difference of channel sounding, mobility of terminals,and additive noise. Effects on the physical layer secret key capacity were quantitatively analyzed in the uniform scattering environment. Based on the time domain statistical characteristics of narrow band wireless channel parameters with noise,a closed-form solution to physical layer secret key capacity in the time domain was derived. Afterwards, simulations in the uniform and non-uniform scattering environment were carried out to demonstrate its validity and applicability, respectively.
physical layer security, physical layer secret key, secret key capacity, uniform scattering environment
s: The National High Technology Research and Development Program of China (863 Program)(No.2015AA01A708), The National Natural Science Foundation of China (No.61171108, No.61471396); China Postdoctoral Science Foundation (No.2016M592990)
TN918.91
A
10.11959/j.issn.1000-436x.2016177
2015-11-04;
2016-07-26
金梁,liangjin@263.net
国家高技术研究发展计划(“863”计划)基金资助项目(No.2015AA01A708);国家自然科学基金资助项目(No.61171108, No.61471396);中国博士后科学基金资助项目(No.2016M592990)

王旭(1990-),男,河南郑州人,国家数字交换系统工程技术研究中心博士生,主要研究方向为无线通信网络与信息安全等。
金梁(1969-),男,北京人,博士,国家数字交换系统工程技术研究中心教授、博士生导师,主要研究方向为无线通信安全等。
刘璐(1988-),男,安徽宿州人,国家数字交换系统工程技术研究中心博士生,主要研究方向为无线通信网络与信息安全等。
李明亮(1988-),男,河南周口人,国家数字交换系统工程技术研究中心博士生,主要研究方向为无线通信网络与信息安全等。
黄开枝(1973-),女,安徽滁州人,博士,国家数字交换系统工程技术研究中心教授、博士生导师,主要研究方向为无线通信安全等。
