电源内阻对双向DC-DC变换器性能的影响

唐酿，盛超，刘昌，朱以顺，翁洪杰，黄辉，袁敞

(1．广东电网有限责任公司电力科学研究院，广东 广州 510080； 2．新能源电力系统国家重点实验室(华北电力大学)，北京 102206)



电源内阻对双向DC-DC变换器性能的影响

唐酿1，盛超1，刘昌2，朱以顺1，翁洪杰1，黄辉1，袁敞2

(1．广东电网有限责任公司电力科学研究院，广东 广州 510080； 2．新能源电力系统国家重点实验室(华北电力大学)，北京 102206)

为解决电源内阻对双向DC-DC变换器性能的影响问题，研究一种考虑电源内阻的双向DC-DC变换器的基础拓扑，建立其状态空间平均模型，并利用小信号分析法得到系统传递函数。通过伯德图分析电源内阻对双向DC-DC变换器控制器性能的影响，提出一种考虑电源内阻的双向DC-DC变换器控制器参数设计方法。以升压模式为例，在PSCAD/EMTDC中验证了电源内阻对双向DC-DC变换器输出电压波动性和暂态稳定性的影响。结果表明，电源内阻会对双向DC-DC变换器的控制性能产生影响，控制参数的设计必须考虑电源内阻。

双向DC-DC变换器；电源内阻；数学模型；小信号分析；控制器参数设计

双向DC-DC变换器是DC-DC变换器的一种，工作在降压和升压两种状态，可实现能量的双向传输，在需要能量双向流动的应用场合可以大幅度减小系统的体积和质量，降低成本，在分布式能源、电力系统、交通、航天航空、计算机和通信、家用电器、国防军工、工业控制等领域得到广泛应用[1]。

1 研究现状

2008年由美国北卡罗莱纳州立大学提出的未来可再生电能传输和管理(future renewable electric energy delivery and management，FREEDM)网络是一种新型的智能微网，其中基于DC-DC变换器的光伏发电拓扑[2]，以及其组网的关键设备固态变压器等都与DC-DC变换器密切相关[3]。

如图1所示，以直流能量池为核心的直流微网中，双向DC-DC变换器是直流电源、负荷、储能与直流母线间的重要媒介，完成了能量在发电侧、负荷侧、储能侧的传输，对促进分布式能源的应用意义重大。此外，由于蓄电池或燃料电池的比功率指标的限制，直接驱动电动机会造成电动机驱动性能恶化，而使用双向DC-DC变换器可将蓄电池组或超级电容器的电压稳定在一个相对较高的水平上，以明显提高电动机的驱动性能，当汽车制动时，逆变器和双向DC-DC变换器可将再生制动的能量存储到电池或超级电容器中[4]。

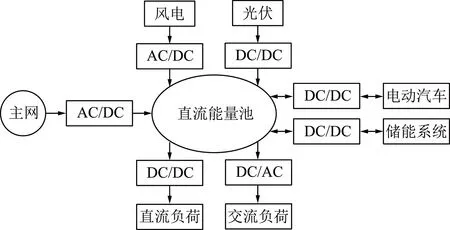
图1 直流微网

本文以图2所示的双向DC-DC变换器拓扑为研究对象，以带电阻的直流电压源等效代替储能电池。文献[5]测量标称为5 Ah的磷酸铁锂单体电池内阻约为10 mΩ。文献[6]考虑了元件等效寄生参数及电感电流纹波等因素，利用峰值电流模型建立了非理想Buck变换器的功率级小信号模型。文献[7]采用状态空间平均法建立了考虑寄生参数的DC-DC 降压开关变换器的数学模型，仿真结果揭示了考虑寄生参数建模的必要性。文献[8]给出了考虑寄生参数的升压斩波电路的模型、仿真及其比例积分微分控制器补偿网络的参数设计过程。文献[9]考虑了寄生参数对Buck-Boost主电路设计的影响，对非理想Buck-Boost电路的校正网络的设计方法和步骤进行阐述。考虑到DC-DC变换器运行的稳定性，文献[10]给出了电压控制型脉冲宽度调制(pulse width modulation，PWM)DC-DC 降压变换器输出阻抗的优化设计准则，并对输出阻抗作标准化定量规范，以确保系统集成后稳定可靠工作。文献[11-12]对双向DC-DC变换器的控制模型进行了研究。上述文献均未阐述电源内阻对双向DC-DC变换器性能可能产生的影响。

本文以图2所示的双向DC-DC变换器为基础，计及电源内阻，建立了图3所示的双向DC-DC变换器工作在电流连续状态下的状态空间平均模型和小信号模型。通过传递函数的幅值和相位裕量约束条件整定控制器参数，得到满足系统稳定要求的比例积分(proportional-integral，PI)参数域。以升压状态下穿越频率2 000 Hz、相位裕量60°为例，得出了双向DC-DC变换器输出电压和控制器受电源内阻影响的结论。总结出考虑电源内阻时双向DC-DC变换器控制系统参数范围整定的一套方法，为实际工程中双向DC-DC变换器的控制器设计提供理论依据。

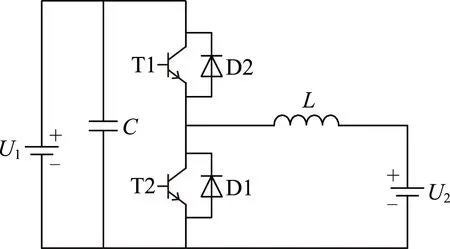
U1、U2—电源电压；C—电容；L—电感；T1、T2—开关晶体管；D1、D2—二极管。图2 双向DC-DC变换器拓扑

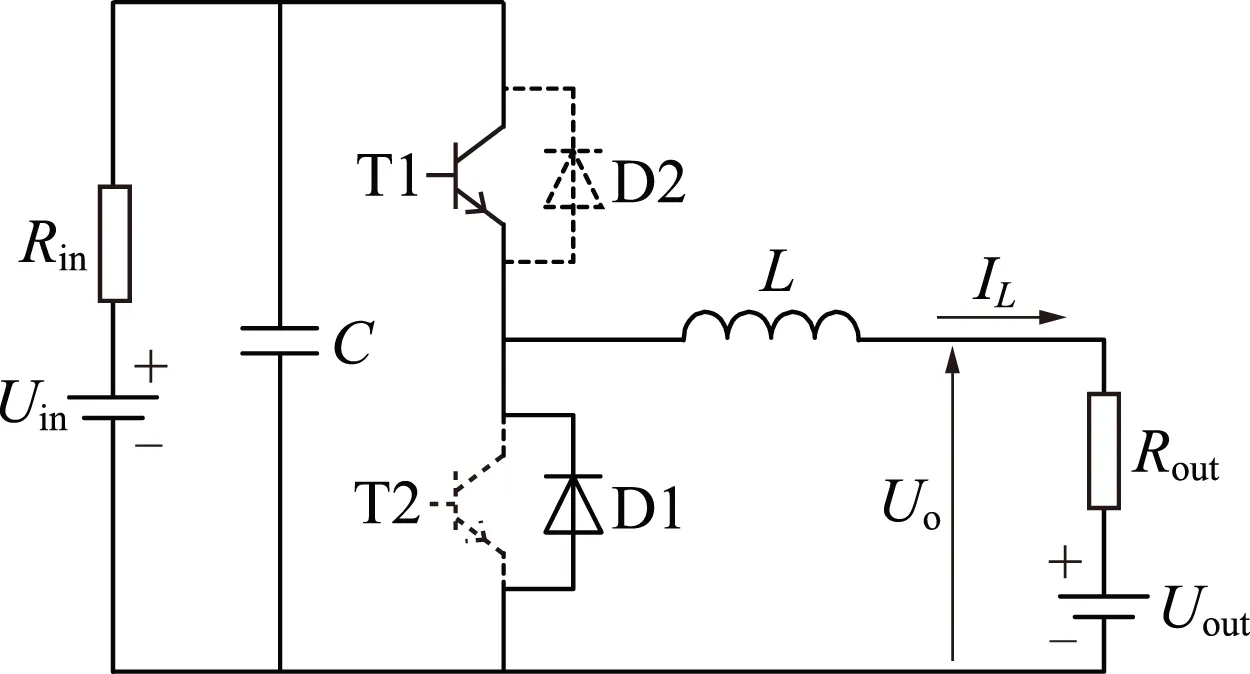
(a)降压状态

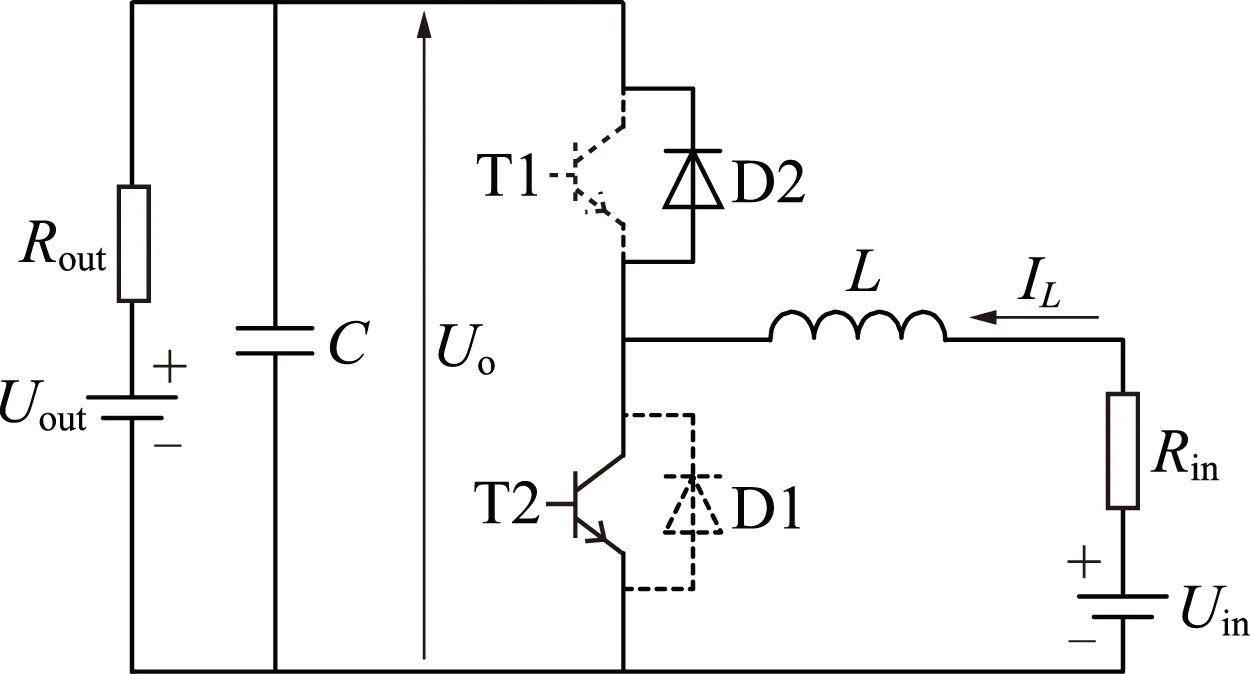
(b)升压状态Uin、Uout—电源电压；Rin、Rout—电源内阻；IL—电感电流；Uo—输出电压。图3 双向DC-DC变换器两种工作状态

2 考虑电源内阻的双向DC-DC变换器状态空间平均法建模

状态空间平均法是按照开关电路中功率开关器件导通和关断的两种状态，对含开关变换器的电路中的状态变量，如电容电压、电感电流的瞬时值在一个周期内进行平均，得到平均状态变量，从而将一个非线性、时变、分段的电路转化为等效的线性、时不变、连续的电路[13]。

对图3所示的双向DC-DC变换器进行状态空间平均建模[14]。为简化公式推导，作如下假设：

a)开关晶体管和二极管是理想器件，可瞬间导通和截止，导通时压降为零，截止时漏电流为零。

b)电感、电容是理想器件，电感工作在线性区且未磁饱和，寄生电阻为零，电容的等效串联电阻为零，仅考虑双侧直流电源存在的内阻。

c)与输出直流电压相比，输出电压中的纹波电压可忽略不计。

d)电感足够大，双向DC-DC变换器工作于电流连续的状态下。

2.1 降压状态

双向DC-DC变换器工作在降压状态，如图4所示，可分为开关导通和关断两种状态。

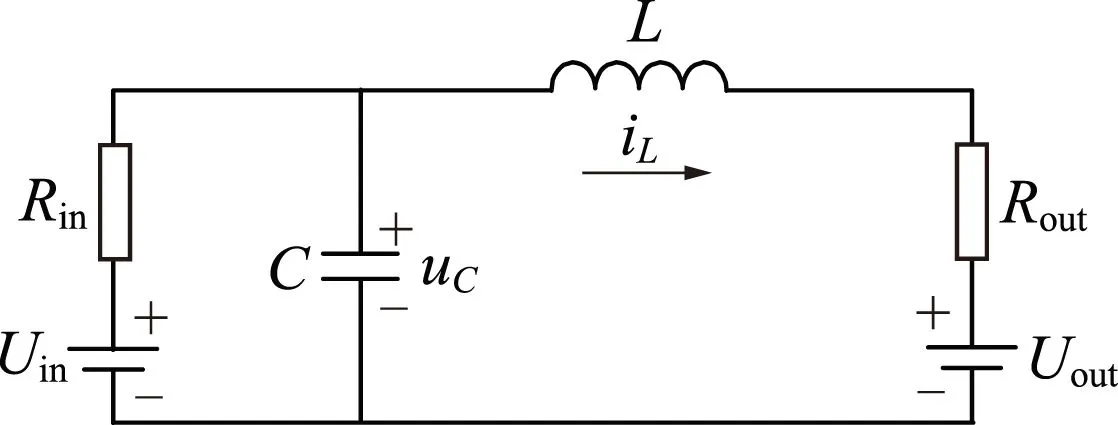
(a)开关器件导通

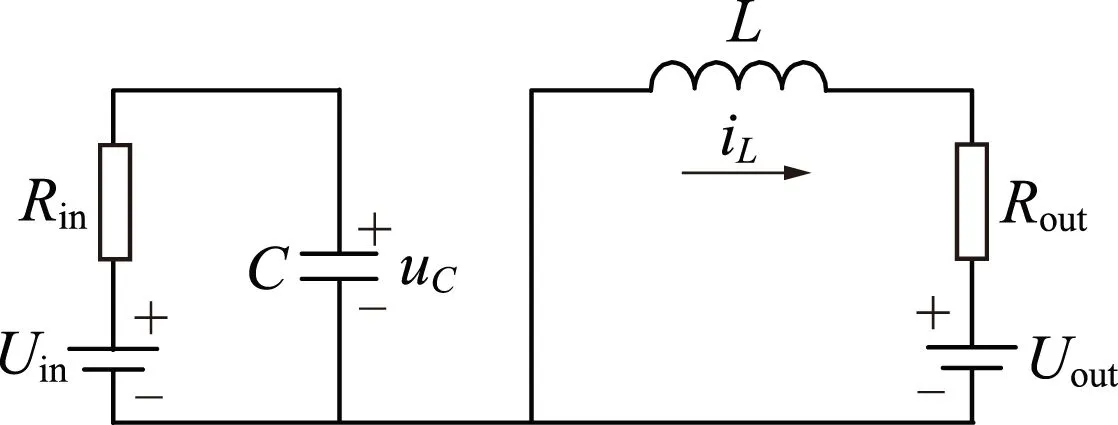
(b)开关器件关断iL—电感电流瞬时值；uC—电容电压瞬时值。图4 双向DC-DC变换器降压状态下的两种工作状态

分别对两种工作方式列写状态方程。开关器件工作于导通状态时，状态方程、输出方程为式(1)；开关器件工作于关断状态时，状态方程、输出方程为式(2)。

(1)

(2)

式(1)、(2)中：t为时间；uC(t)为电容电压瞬时值；iL(t)为电感电流瞬时值；uo(t)为输出电压瞬时值；uin(t)为输入侧电压源电压瞬时值；uout(t)为输出侧电压源电压瞬时值。

由上述方程建立小信号模型，即

(3)

式中：D为稳态时的占空比；d(t)为瞬时占空比；“^”表示各量的小扰动量。

将式(3)拉普拉斯变换后得到变换器占空比至输出电压的传递函数

(4)

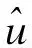
列写静态状态平均方程、输出方程为：

(5)

由式(5)得到稳态时的电感电流、电容电压、输出电压、占空比的表达式：

(6)

PWM调制器的传递函数

(7)

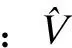
反馈分压网络传递函数

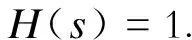
(8)

被控对象的传递函数

(9)

2.2 升压状态

双向DC-DC变换器工作在升压状态，同样可分为开关导通和关断两种状态，如图5所示。

我国为了缓解交通压力，建立了各种桥体，如城市立交桥、高架桥、过街天桥等。城市绿化的相关工作人员可以利用这一条件，在桥身和立柱上设计种植槽和垂挂吊篮。目前，在桥面与桥身上可以设置金银花、牵牛花等植物，在桥柱上则可以配置一些凌霄、爬山虎等攀援植物，这种绿化形式可以在不影响驾驶员驾驶的情况下，起到美化城市和净化空气的作用。

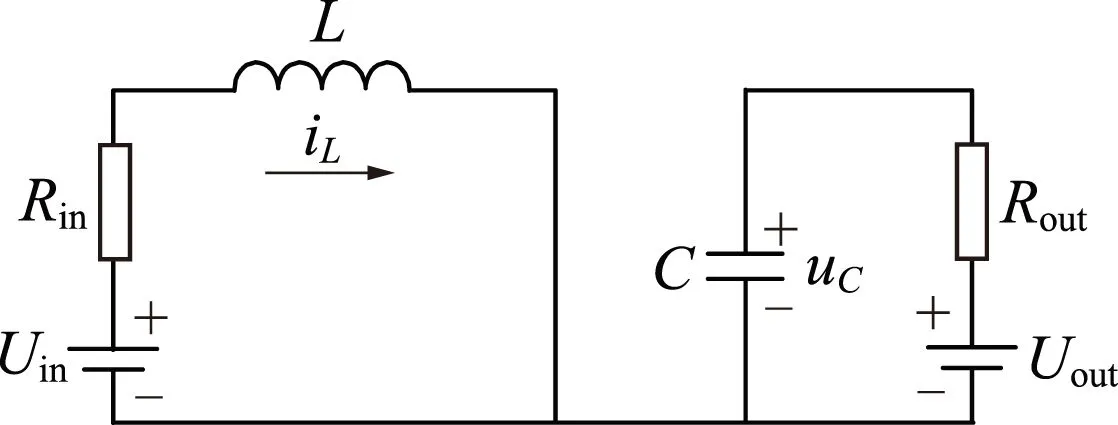
(a)开关器件导通

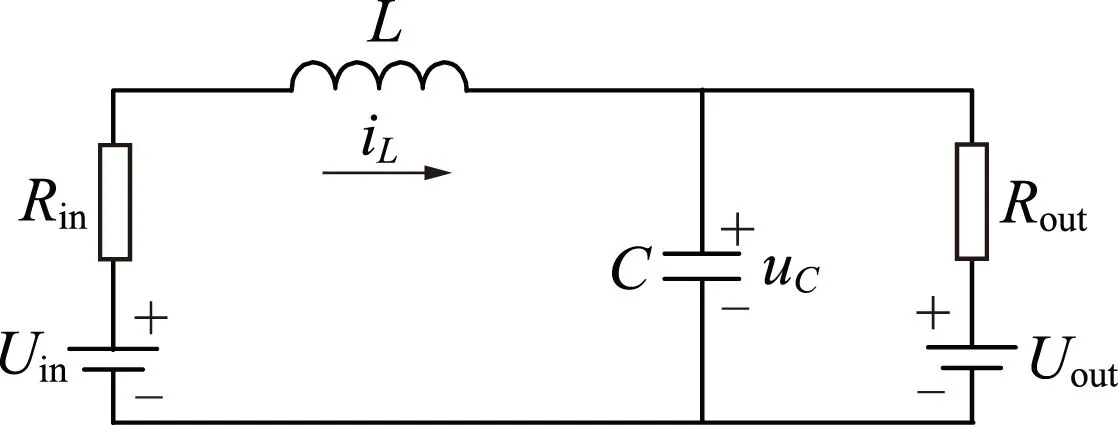
(b)开关器件关断图5 双向DC-DC变换器升压状态下的两种工作状态

下面分别对两种工作方式列写状态方程。开关器件工作于导通状态时，状态方程、输出方程为式(10)；开关器件工作于关断状态时，状态方程、输出方程为式(11)。

表1 双向DC-DC电路算例参数

工作状态Uin/VUout/VUo/Vfs/kHzL/mHC/μFfg/kHzRin/Ω考虑电源内阻不考虑电源内阻Rout/Ω考虑电源内阻不考虑电源内阻降压状态200809010147001～2100.0110.001升压状态8020022510147001～210.001100.01

注：fs为开关频率，fg为穿越频率。

图5 双向DC-DC变换器升压状态下的两种工作状态

下面分别对两种工作方式列写状态方程。开关器件工作于导通状态时，状态方程、输出方程为式(10)；开关器件工作于关断状态时，状态方程、输出方程为式(11)。

(10)

由上述方程建立小信号模型，即

(12)

式中D′=1-D。

将式(12)拉普拉斯变换后得到变换器占空比至输出电压的传递函数

(13)

(14)

由式(14)得到稳态时的电感电流、电容电压、输出电压、占空比的表达式：

(15)

PWM调制器的传递函数、反馈分压网络传递函数与降压状态相同，这里不再赘述。

被控对象的传递函数

(16)

3 双向DC-DC变换器控制系统参数设计

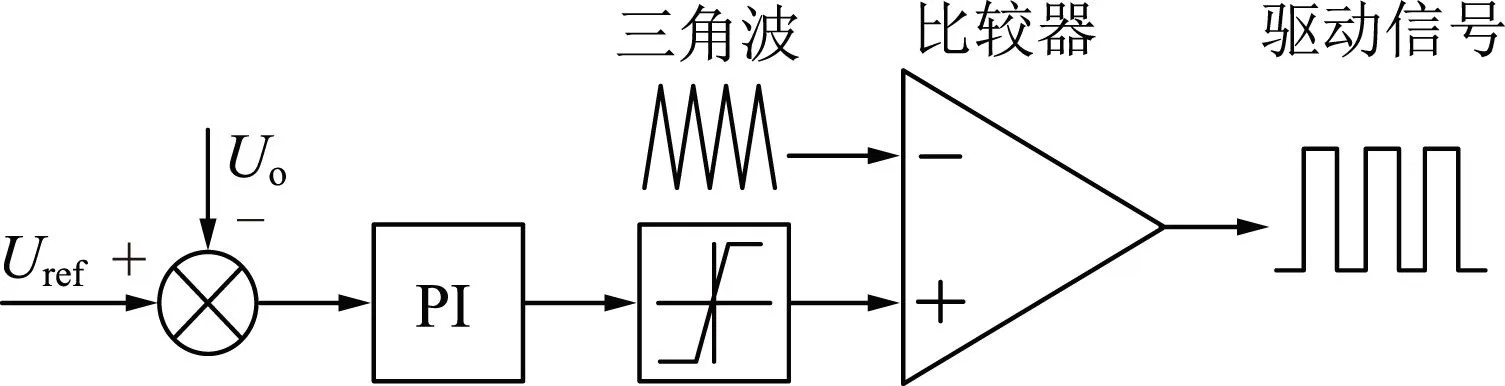
Uref—参考电压。图6 双向DC-DC电路控制系统

双向DC-DC电路算例参数见表1。

幅值裕量、相位裕量的约束条件为

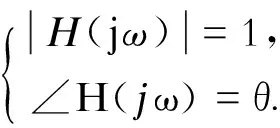
(17)

其中

(18)

式(17)、(18)中：ω为频率；H(jω)为包含控制器的被控对象传递函数；Go(jω)为被控对象传递函数；K为比例常数；T为积分时间常数；θ为相位裕量，θ的取值范围设置为π/4～π/3。

选择开关频率fs=10 kHz，穿越频率fg应小于1/5的开关频率，设置为1 000～2 000 Hz，可根据穿越频率和相位裕量的范围确定比例常数K、积分时间常数T的分布范围(如图7所示)。

由图7可以看出，不考虑电源内阻与考虑电源内阻的双向DC-DC变换器控制参数取值范围存在很大差异，实际工程中存在控制参数的选择问题。

4 仿真结果及对比分析

以升压电路为例，输出电压参考值Uref为225 V，分别对不考虑电源内阻状态和考虑电源内阻状态进行控制器性能分析及时域仿真，以相位裕量60°，穿越频率2 000 Hz为例，如图8所示。

考虑电源内阻的双向DC-DC变换器控制器在保证相位裕量60°、穿越频率2 000 Hz时的控制参数为K=23.808 5、T=32.2 μs，时域仿真和系统开、闭环传递函数分别为图8(c)、8(d)，其中相位裕量、穿越频率与理论值相符，输出电压范围224.9～225.2 V，误差为-0.044%～0.089%．不考虑电源内阻时满足相位裕量60°、穿越频率2 000 Hz时的控制器参数为K=0.001 37、T=0.73 μs，将其作为考虑电源内阻的双向DC-DC变换器控制器参数，得到时域仿真和系统开、闭环传递函数分别为图8(a)、8(b)，其中相位裕量121°，穿越频率203 Hz，与理论值不符合，输出电压范围223.2～226.6 V，误差为-0.8%～0.711%，误差最大为前者的18.18倍。

综上所述，由于实际双向DC-DC变换器中电源内阻的存在直接导致传递函数的变化，使得不考

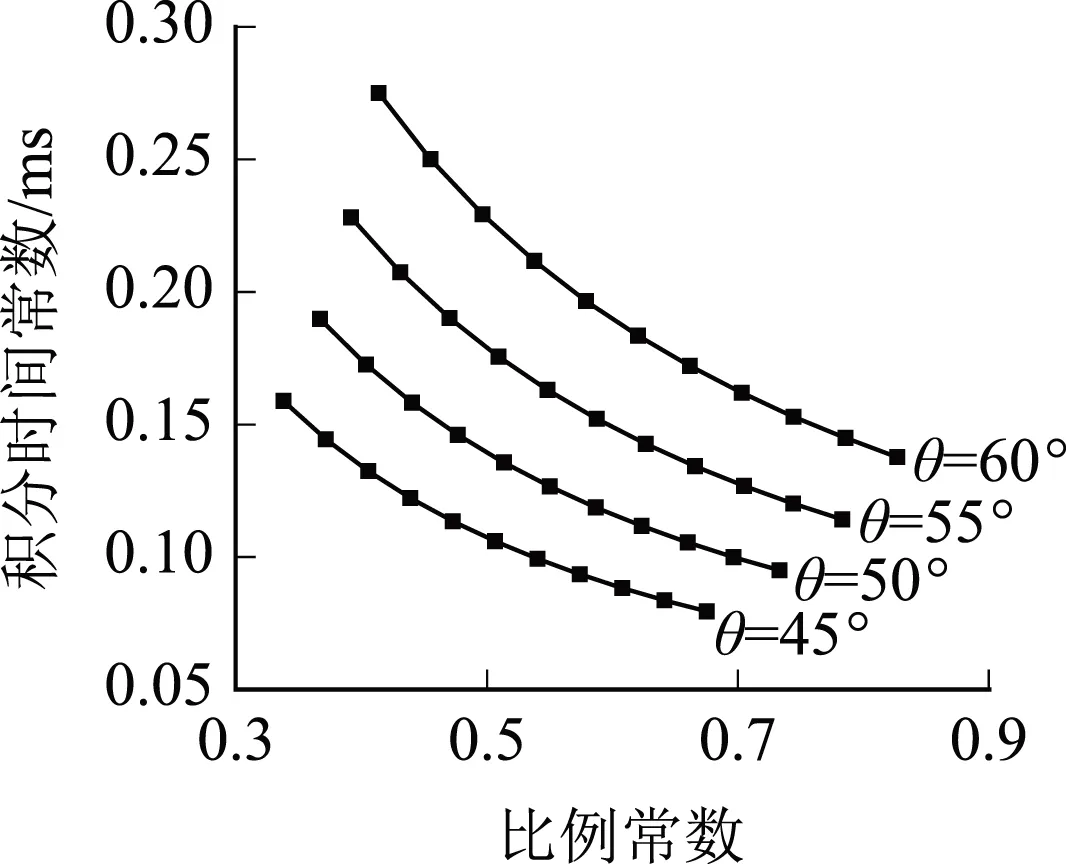
(a)降压状态(不考虑电源内阻)

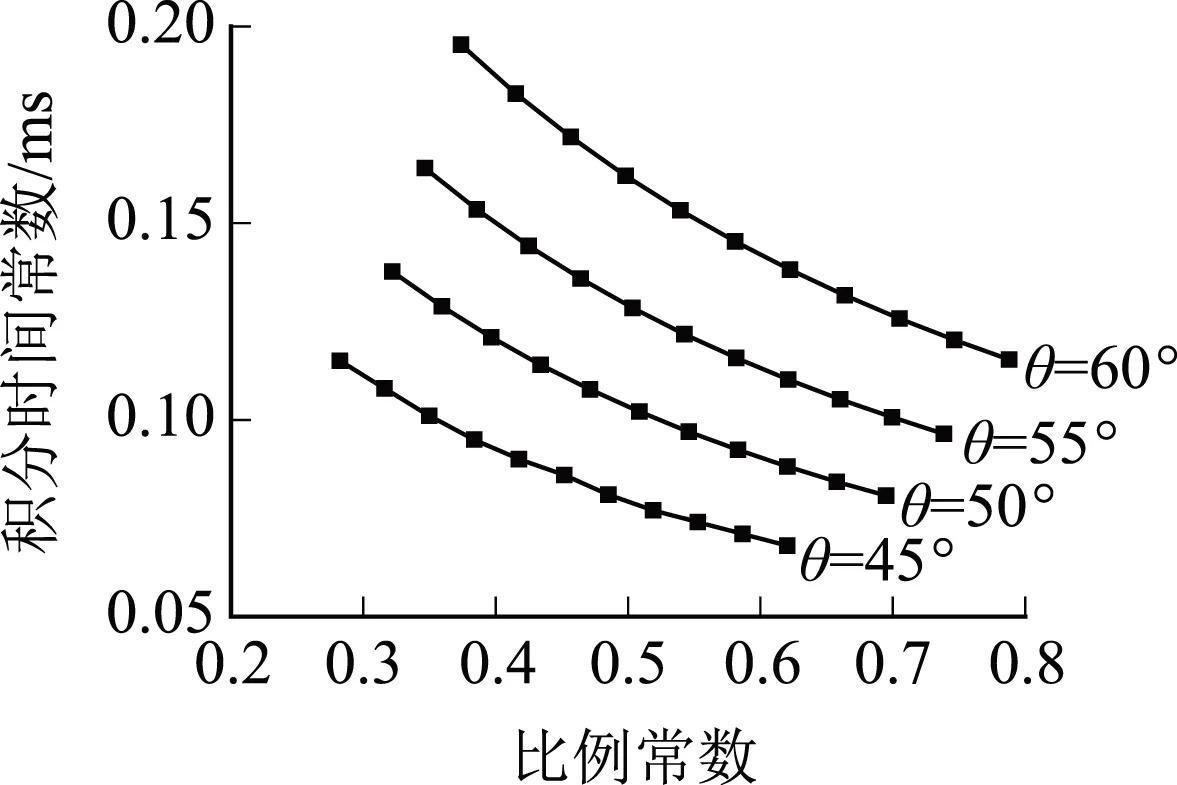
(b)降压状态(考虑电源内阻)

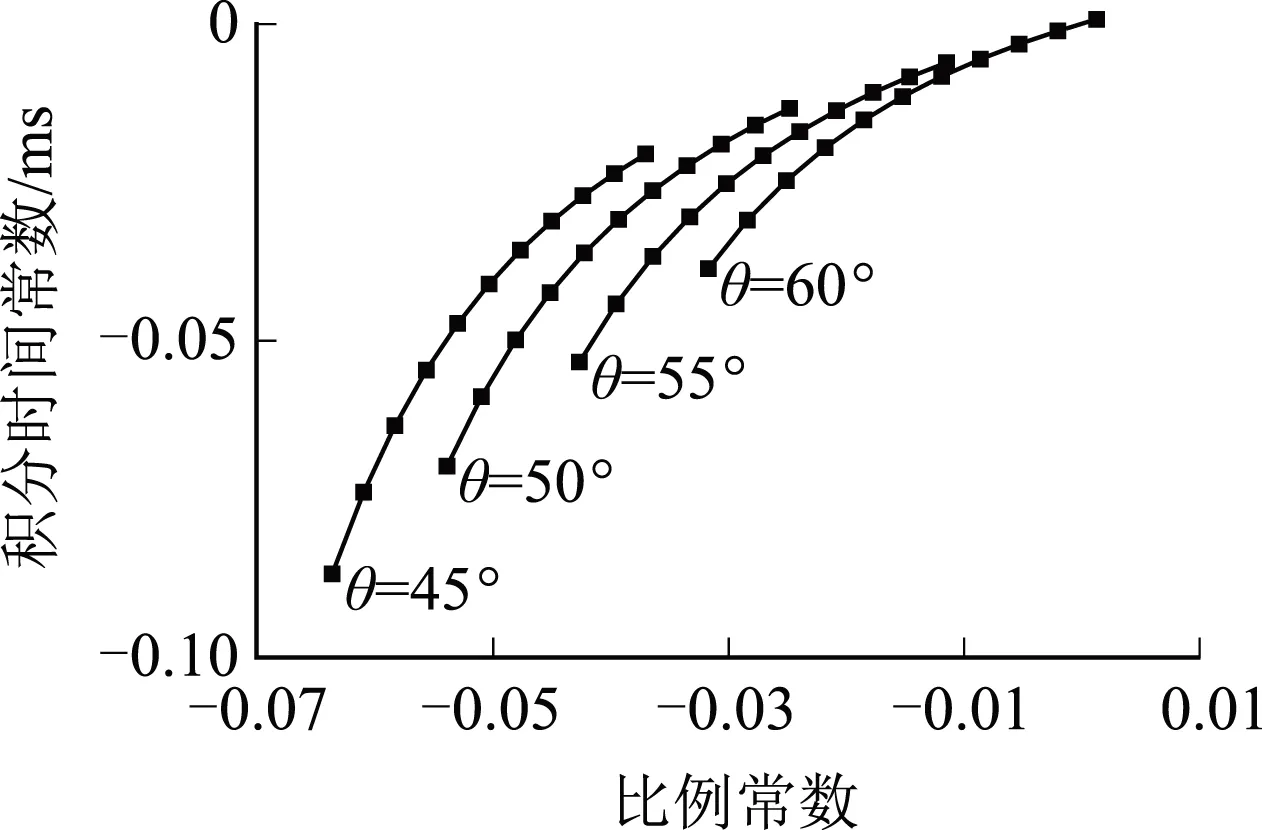
(c)升压状态(不考虑电源内阻)

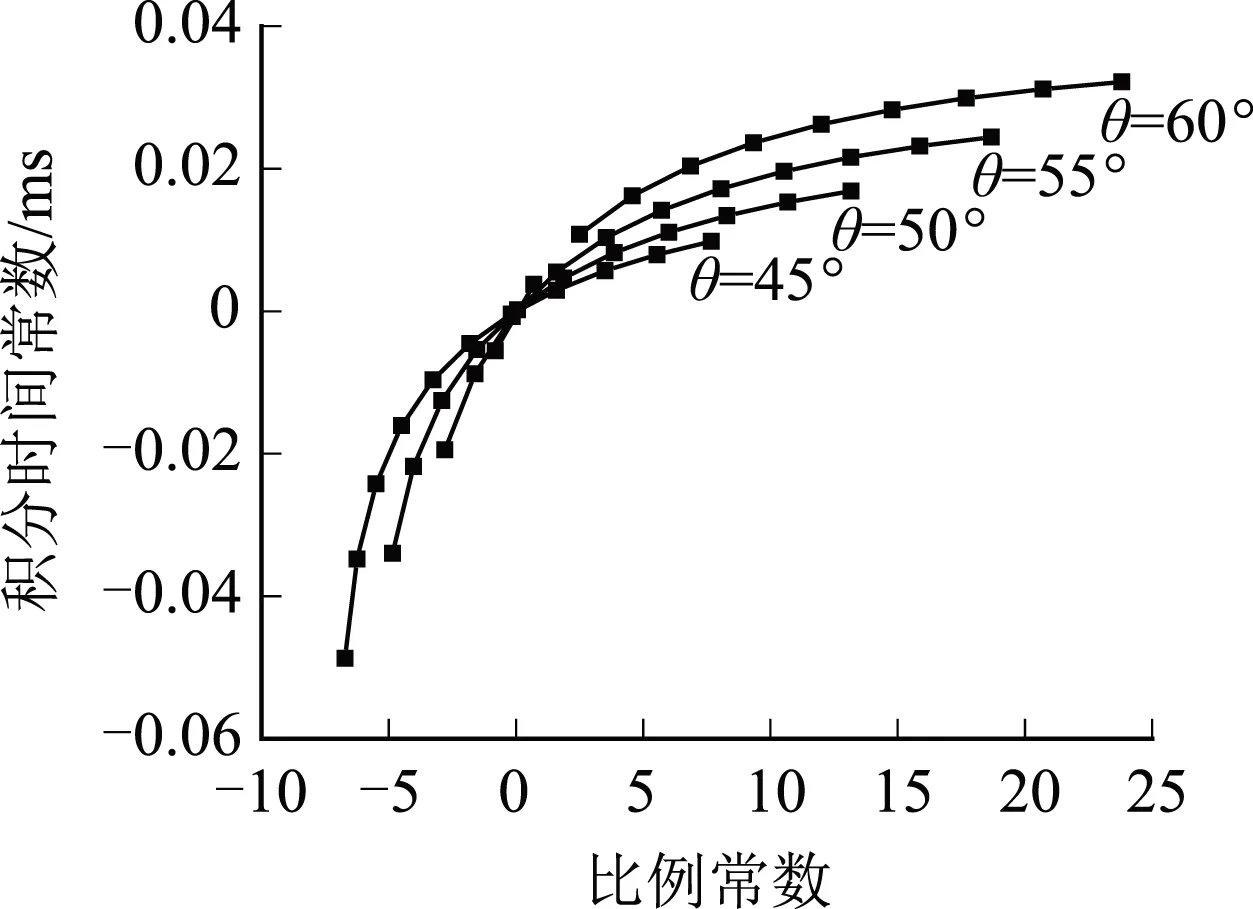
(d)升压状态(考虑电源内阻)图7 控制参数取值范围

虑电源内阻时设计的控制器参数无法满足考虑电源内阻的控制器的需要，由此可见双向DC-DC变换器控制器参数设计时考虑电源内阻的必要性。

时域仿真中，t=1.0 s时输入电压由80 V瞬时变为100 V，产生20 V的阶跃电压，如图9所示。图9(a)为不考虑电源内阻情况下设计的参数K=0.001 37、T=0.73 μs，稳定输出电压222.3～229.6 V，电压峰谷值差为7.3 V；图9(b)为考虑电源内阻情况下设计的参数K=23.808 5、T=32.2 μs，稳定输出电压222.8～227.4 V，电压峰谷值差为4.6 V。二者在一段时间后均达到稳定状态，由以上数据分析，不考虑电源内阻状态下设计的参数对这一阶跃电压的响应更为敏感，相反考虑电源内阻状态下的参数可以有效抑制电压突变，提高了输出电压的暂态稳定性，再次证明了实际工程中控制器设计考虑电源内阻的必要性。

(a)不考虑电源内阻控制参数(K=0.001 37，T=0.73 μs)输出电压

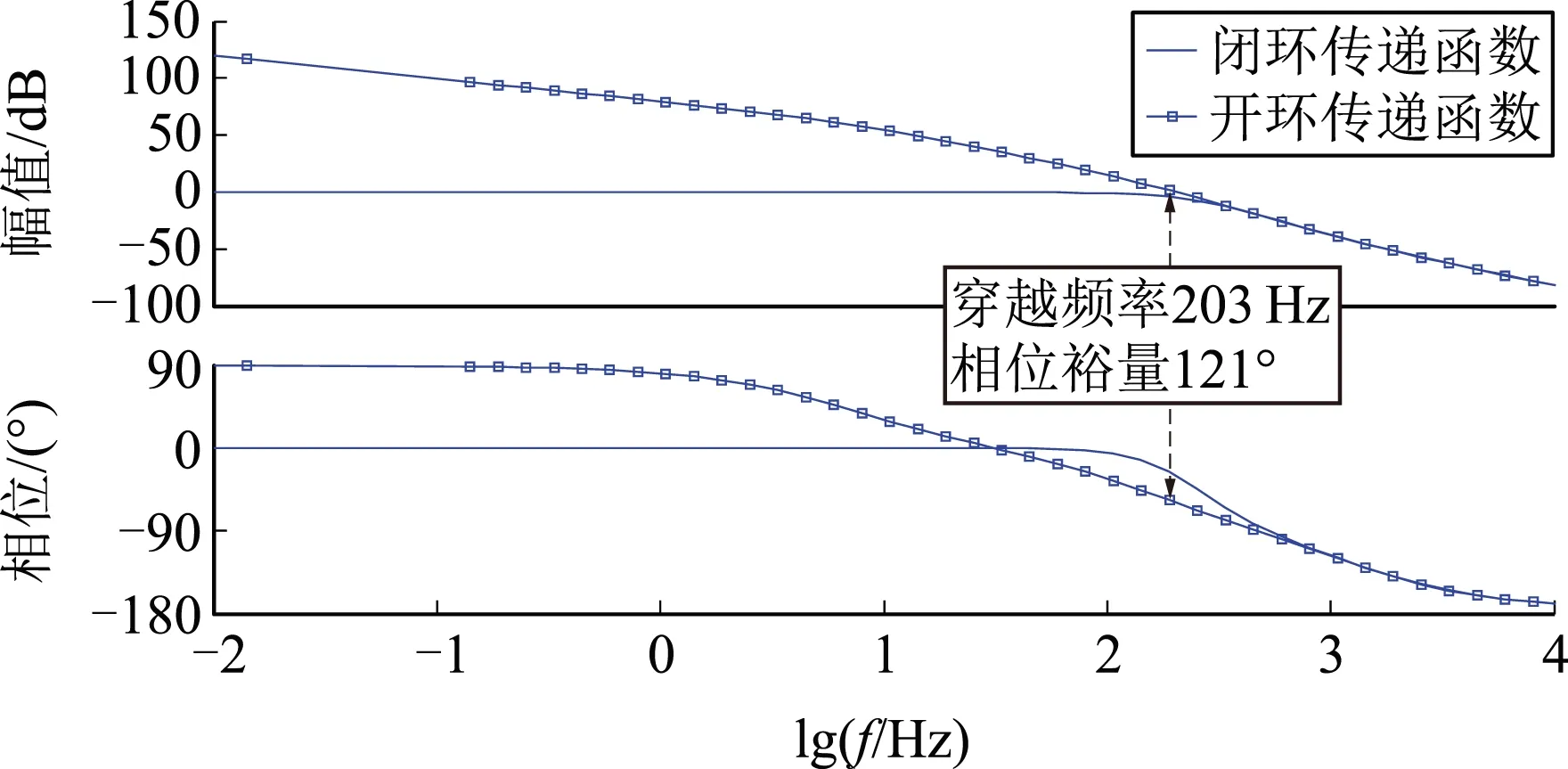
(b)不考虑电源内阻控制参数(K=0.001 37，T=0.73 μs)系统伯德图

(c)考虑电源内阻控制参数(K=23.808 5，T=32.2 μs)输出电压

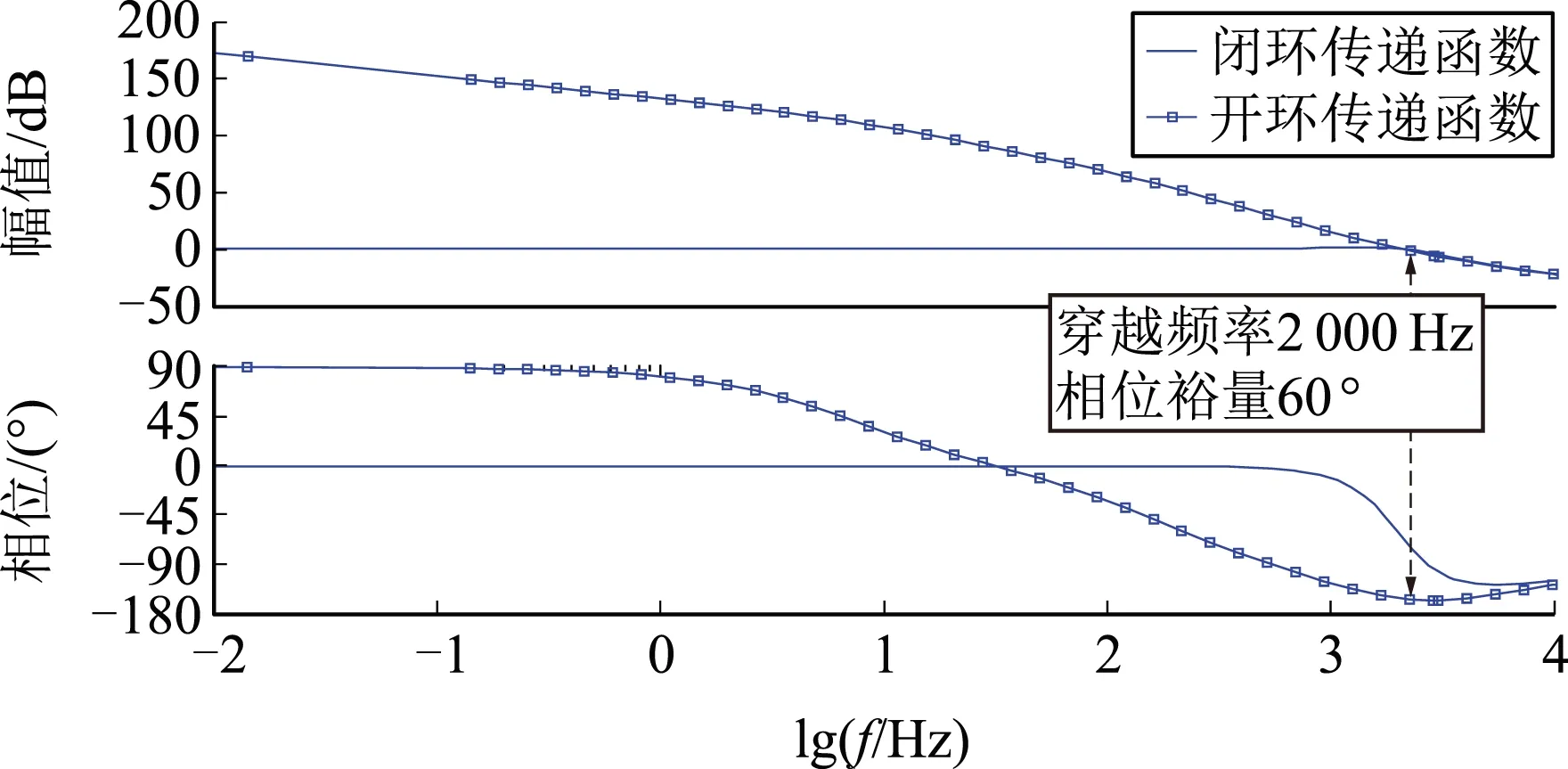
(d)考虑电源内阻控制参数(K=23.808 5，T=32.2 μs)系统伯德图f—输入信号频率。图8 参数仿真验证及伯德图

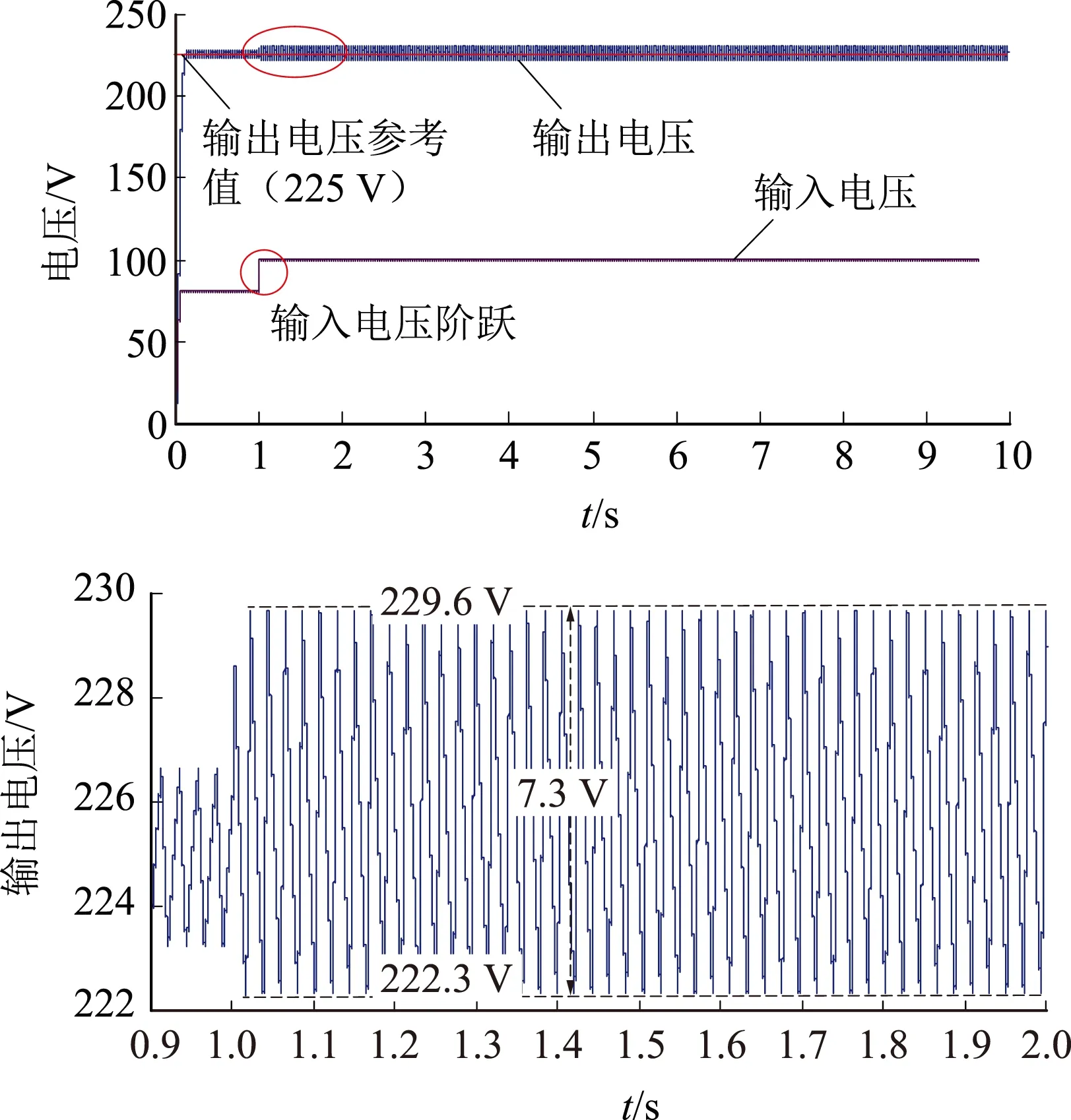
(a)不考虑电源内阻控制参数(K=0.001 37，T=0.73 μs)的输出电压

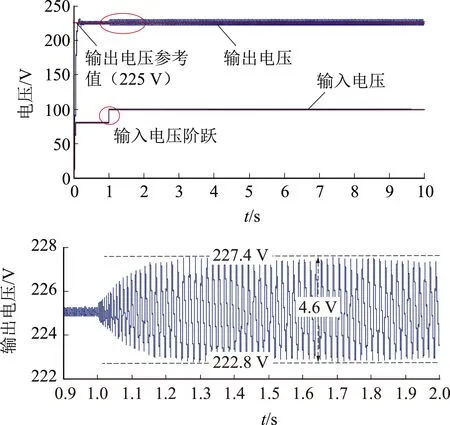
(b)考虑电源内阻控制参数(K=23.808 5，T=32.2 μs)的输出电压图9 输入电压阶跃时两组参数下的输出电压

5 结论

本文基于双向DC-DC变换器的基础拓扑，提出一种考虑电源内阻的双向DC-DC变换器控制器参数设计方法。通过对系统伯德图的分析，研究了电源内阻对双向DC-DC变换器控制器性能的影响，得到以下结论：

a)所提的控制器参数设计方法和系统伯德图可准确地分析出电源内阻对双向DC-DC变换器控制器性能的影响；

b)仿真和实验结果表明，电源内阻会对双向DC-DC变换器的控制性能产生影响，不考虑电源内阻时设计的控制器参数无法满足实际考虑电源内阻的控制器的需要，考虑电源内阻是十分必要的。

本文提供了一套考虑电源内阻的双向DC-DC变换器控制器参数设计方法，为其控制器设计和工程应用提供了理论参考。

[1] 张方华，朱成花，严仰光．双向DC-DC变换器的控制模型[J].中国电机工程学报，2005，25(11)： 46-49.

ZHANG Fanghua，ZHU Chenghua，YAN Yangguang. The Controlled Model of Bidirectional DC-DC Converter[J].Proceedings of the CSEE，2005，25(11)： 46-49.

[2] LIANG Z G，GUO R，LI J，et al．A High-efficiency PV Module-integrated DC/DC Converter for PV Energy Harvest in FREEDM Systems[J].IEEE Transactions on Power Electronics，2011，26(3)：899.

[3] SHE X，HUANG A Q，NI X J. Current Sensorless Power Balance Strategy for DC/DC Converters in a Cascaded Multilevel Converter Based Solid State Transformer [J]. IEEE Transactions on Power Electronics，2014，29(1)：17-22.

[4] 夏超英，刘奎，郭熠．电动汽车用全数字双向DC-DC变换器的实现[J].电力电子技术，2006，40(1)：70.

XIA Chaoying，LIU Kui，GUO Yi．Implementation of a Bi-directional DC/DC Converter in the Electric Vehicle[J]. Power Electronics，2006，40(1)：70.

[5] 潘进. 大容量储能系统电池管理技术研究[D].哈尔滨：哈尔滨工业大学，2012.

[6] 解光军，徐慧芳．峰值电流模式控制非理想Buck变换器系统建模[J]. 中国电机工程学报，2012，32(24)：52-58.

XIE Guangjun，XU Huifang．Modeling of Current Programmed Mode Non-ideal Buck Converter Systems[J].Proceedings of the CSEE，2012，32(24)：52-58.

[7] 葛茂艳，谢利理，吴喜华．非理想Buck变换器的建模及仿真[J].计算机仿真，2010，27(4)：333-336.

GE Maoyan，XIE Lili，WU Xihua. Modeling and Simulation of Unideal Buck Converter[J].Computer Simulation，2010，27(4)：333-336.

[8] 程心．非理想DC-DC开关变换器的建模分析与仿真[D].合肥：合肥工业大学，2009.

[9] 李宇．Buck-Boost变换器的研究[D].南京：南京航空航天大学，2006.

[10] 王建华，张方华，龚春英，等．电压控制型Buck DC/DC变换器输出阻抗优化设计[J]. 电工技术学报，2007，22(8)：18-23. WANG Jianhua，ZHANG Fanghua，GONG Chunying，et al. Study of Output Impedance Optimization for Voltage Mode Control Buck DC/DC Converter[J].Transactions of China Electrotechnical Society，2007，22(8)：18-23.

[11] 孙驰，毕增军，魏光辉．一种新颖的三相四桥臂逆变器解耦控制的建模与仿真[J].中国电机工程学报，2004，24(1)：124-130.

SUN Chi，BI Zengjun，WEI Guanghui．Modeling and Simulation of a Three-phase Four-leg Inverter Based on a Novel Decoupled Control Technique[J].Proceedings of the CSEE，2004，24(1)：124-130.[12] 林维明，黄是鹏，张冠生，等．具有快速负载动态响应的DC/DC开关变换器开环控制新策略[J].中国电机工程学报，2001，21(9)：78-81.

LIN Weiming，HUANG Shipeng， ZHANG Guansheng， et al． A New Open-loop Control Strategy for a DC-DC Switching Converter with Fast Load Transient Response[J]. Proceedings of the CSEE，2001，21(9)：78-81.

[13] TANG W，LEE F C，RIDLEY R B．Small-signal Modeling of Average Current-mode Control [J].IEEE Transactions on Power Electronics，1993，8(2)：112-119.

[14] 徐德鸿．电力电子系统建模及控制[M].北京：机械工业出版社，2006：25-32.

(编辑 彭艳)

Influence of Source Impedance on Performance of Bidirectional DC-DC Converter

TANG Niang1, SHENG Chao1, LIU Chang2, ZHU Yishun1, WENG Hongjie1, HUANG Hui1, YUAN Chang2

(1. Electric Power Research Institute of Guangdong Power Grid Co., Ltd., Guangzhou, Guangdong 510080, China; 2. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (North China Electric Power University), Beijing 102206, China)

In order to solve the problem of influence on bidirectional DC-DC converter(BDC) by source impedance, this paper studies a kind of fundamental topology considering source impedance, establishes an average model for its state space and uses small signal analysis method to get transfer function of the system. Based on bode diagram, it analyzes influence of source impedance on performance of the controller of BDC and presents a kind of design method for controller parameters of BDC considering source impedance. Taking boost mode for an example, it verifies influence of source impedance on volatility and transient stability of output voltage of BDC in PSCAD/EMTDC. Results indicate that source impedance has an effect on controlling performance of BDC and it is necessary to consider source impedance for designing control parameters.

bidirectional DC-DC converter; source impedance; mathematical model; small signal analysis; parameter design of controller

2016-05-03

广东电网有限责任公司科技支撑计划项目 (GDKJ00000045)

10.3969/j.issn.1007-290X.2016.10.005

TM46

A

1007-290X(2016)10-0024-07

唐酿(1984)，男，湖南湘潭人。工学博士，主要从事电力电子在电力系统中的应用方面工作。

盛超(1972)，男，安徽桐城人。高级工程师，工学硕士，从事FACTS技术、电能质量等方面的研究。

刘昌(1992)，男，山东济宁人。在读硕士研究生，从事电力电子在电力系统中的应用方面研究。