不同索径拉索风雨激励稳定性影响试验研究
2016-11-23葛耀君
常 颖, 罗 维, 赵 林, 葛耀君
(同济大学 土木工程防灾国家重点实验室,上海 200092)
不同索径拉索风雨激励稳定性影响试验研究
常 颖, 罗 维, 赵 林, 葛耀君
(同济大学 土木工程防灾国家重点实验室,上海 200092)
在实验室条件下采用人工模拟降雨成功重现了两种直径拉索的风雨激振现象,系统研究了风速、雨强、结构阻尼比等参数对风雨激振的影响以及螺旋线对拉索振动的抑制作用.试验表明,不同折算风速下拉索大幅振动的机理存在一定差异:在较高折算风速下拉索振动更类似限幅的准驰振振动;在低折算风速下拉索的振动与尾流中的低频涡关系更密切,即是一种涡致振动.
拉索; 风雨激振; 人工降雨试验; 螺旋线
拉索风雨激振是一种拉索在风雨共同作用下发生的大幅低频振动,是目前已知拉索振动中振幅最大、危害最严重的一种振动.日本的Hikami和Shiraishi[1]在主跨为405 m的Meiko桥上首次实测到了拉索的风雨激振,由此拉开拉索风雨激振研究的序幕,已有的现场实测[2-3]、风洞试验[4-7]、数值模拟[8-10]都对该现象进行了研究分析.根据已有文献可知,拉索风雨激振是一种限速、限幅振动,主要发生于有光滑PE 索套的斜拉索,直径范围约为80~200 mm.风雨振动的振动频率在3.0 Hz范围内,振动以低阶模态为主,发振时的风速范围在6.0~15.0 m·s-1之间,相应的折算风速Ur约在20~90之间,过高或过低的风速下不易发生风雨激振.
当拉索发生风雨激振时,拉索上下表面各有一条雨水形成的水线,沿倾斜的拉索向下流动,水线随着拉索振动在拉索表面振荡.顾明等[11]对带人工水线的三维拉索模型进行了测压试验,得到了不同风向角下拉索和水线的气动力系数,在此基础上建立了拉索风雨激振的理论模型.研究表明,拉索气动力存在突变区域,并对应于拉索风雨激振的大幅振动区域.陈文礼[12]用超声波测试系统对风雨激振过程中水线的动力特性进行实时监测,测得拉索表面上、下两条水线的等高线图时程,得到下水线相对稳定,上水线作周向振荡的现象,并且振荡主频与拉索振动频率非常接近,振幅较大.同时上水线振荡范围及其平衡位置位于气动力突变的区域,在该区域内,会给斜拉索附加气动负阻尼,二者结合易使拉索产生大幅度共振.许林汕[13]发现,在两种风雨条件下拉索容易发生风雨激振,高风速小雨量和低风速大雨量区域.低风速风雨激振时,雨水螺旋状滑落,无明显上水线,高风速风雨激振时,有明显上、下两条水线.
迄今为止关于拉索风雨激振的机理有不同的理论.水线驰振理论[14-15]认为,在水线位置及运动的影响下,拉索升力系数存在负斜率段或突变区,从而引起的类似驰振的限幅运动.李永乐[16]等通过数值计算,并从能量的角度出发证明了该种具有自激和限幅双重特性的准驰振振动.Matsumoto提出的以轴向流理论[16]为基础的高折算风速涡致振动理论[17-18]和卡门涡抑制理论[19-20]认为,轴向流对于风雨激振的产生非常重要.该系列理论的核心思想为,轴向流以及特定位置的水线会对卡门涡脱落产生影响,削弱卡门涡的强度,导致气动不稳定性,从而导致风雨激振的发生.大多水线驰振理论及其相应的模型,都忽略了轴向流的影响,这是与轴向流理论、高折算风速涡致振动理论以及卡门涡抑制理论的最大不同.另外,在水线的作用方面,一些水线驰振理论认为水线的运动是风雨激振的必不可少的条件[11,21],而高折算风速涡致振动理论以及卡门涡抑制理论着重于水线的位置对风雨激振的影响.
本文采用人工降雨的方式,重现了两种直径拉索的风雨激振现象.由于发生风雨激振的拉索直径范围为80~200 mm,该范围内小直径的拉索不易发生振动,选取中等粗细的139 mm直径的拉索以及较粗的200 mm直径的拉索进行风洞试验,以检验不同尺度拉索的气动稳定性.根据已有研究可知,对中等直径的拉索风雨激振的试验较多,而对于大直径的拉索人工降雨试验尚不足.随着斜拉桥向更大跨度发展,大直径拉索关于风雨激振方面的考虑是必要的.试验具有较好的重复性;同时还研究了结构阻尼比对风雨激振的影响,检验了螺旋线对风雨激振的抑制效果;最后,根据试验现象和现有理论,对风雨激振的产生机理进行探索.
1 风雨振试验
试验在同济大学土木工程防灾国家重点实验室TJ-1直流式边界层风洞的射流区进行.该风洞试验段截面尺寸为1.8 m×1.8 m(宽×高),风速调节范围为0.5~30.0 m·s-1.风洞尾部扩散段出口处接有射流喷管,形成自由射流区,其出口截面直径为2.4 m.
同济大学TJ-1风洞射流段出口处安装有全自动测控便携式模拟降雨机,采用3种不同规格的垂直全喷式雨滴模拟专用喷头,叠加成一个雨滴喷射组.这种组合既可有较大雨强变化,又可保证雨滴模拟效果,从而形成从小到大的雨强连续可调,雨滴形态,降雨均匀度与自然降雨相似的人工自动模拟降雨.图1为人工降雨系统示意图.

图1 人工降雨系统示意图
试验采用同济大学风洞实验室拉索悬挂支架作为拉索悬挂系统,并将其放在风洞射流区,支架中心位于风洞出口2 m处,降雨中心、风场中心、支架中心位于同一平面内,拉索通过弹簧与支架相连,选取合适的弹簧使得拉索模型轴线与支架上平面相平行,模型上端采用钢丝与支架轴向连接,布置图及模型空间位置示意图如图2与图3所示.

图2 试验悬挂支架图

图3 模型空间位置示意图
试验模型采用实际拉索节段,但由于其质量过大,仅取拉索外包护套,即抽出其钢丝部分.模型几何缩尺比为1∶1,试验风速比为1∶1,模型长度2 000 mm,拉索模型的Reynolds数和Strouhal数与实桥拉索一致,其中雷诺数取值范围为1.2万~13.4万.模型放宽了质量阻尼参数Scruton数的要求,以苏通大桥139 mm直径拉索为例,实桥拉索质量77.72 kg·m-1,模型质量3.65 kg·m-1,模型与实索的Scruton数比值1∶21.3.由于模型质量小于实桥拉索质量,模型Scruton数减小,模型振幅与实际拉索振幅相比,试验结果是偏于保守的.
当来流速度分别为10 m·s-1和15 m·s-1时,射流段风速在距出口截面2 m上的分布情况如图4所示.表1为风速统计数据,U为截面平均风速;σ为截面各点风速均方差;μ为截面各点风速标准差.

U=10 m·s-1

U=15 m·s-1
拉索节段模型具体参数如表2.拉索振动信号采用加速度传感器采集,频率为204.8 Hz.光索工况如表3所示.同时,研究了阻尼和螺旋线抑振措施对风雨激振的影响,抑振措施拉索试验工况如表4所示.

表2 拉索节段模型参数

表3 光索模型人工降雨试验工况安排

表4 带有螺旋线的拉索模型人工降雨试验工况
2 试验结果
2.1 Φ139拉索风雨激振试验
根据现场实测资料以及风雨环境试验结果可知,拉索仅在特定的空间姿态下发生风雨激振现象.试验中,在倾角α=25°、风偏角β=25°的空间姿态下,拉索发生了大幅风雨激振.在拉索发生风雨激振时,振动可以看作是等振幅的,且其振动频率与模型系统的固有频率非常接近.光索加速度时程及功率皮密度如图5所示.图6给出不同雨强下拉索振幅随风速的变化,图7给出4种风速下(6,7,8,9 m·s-1)拉索振幅随雨强的变化.
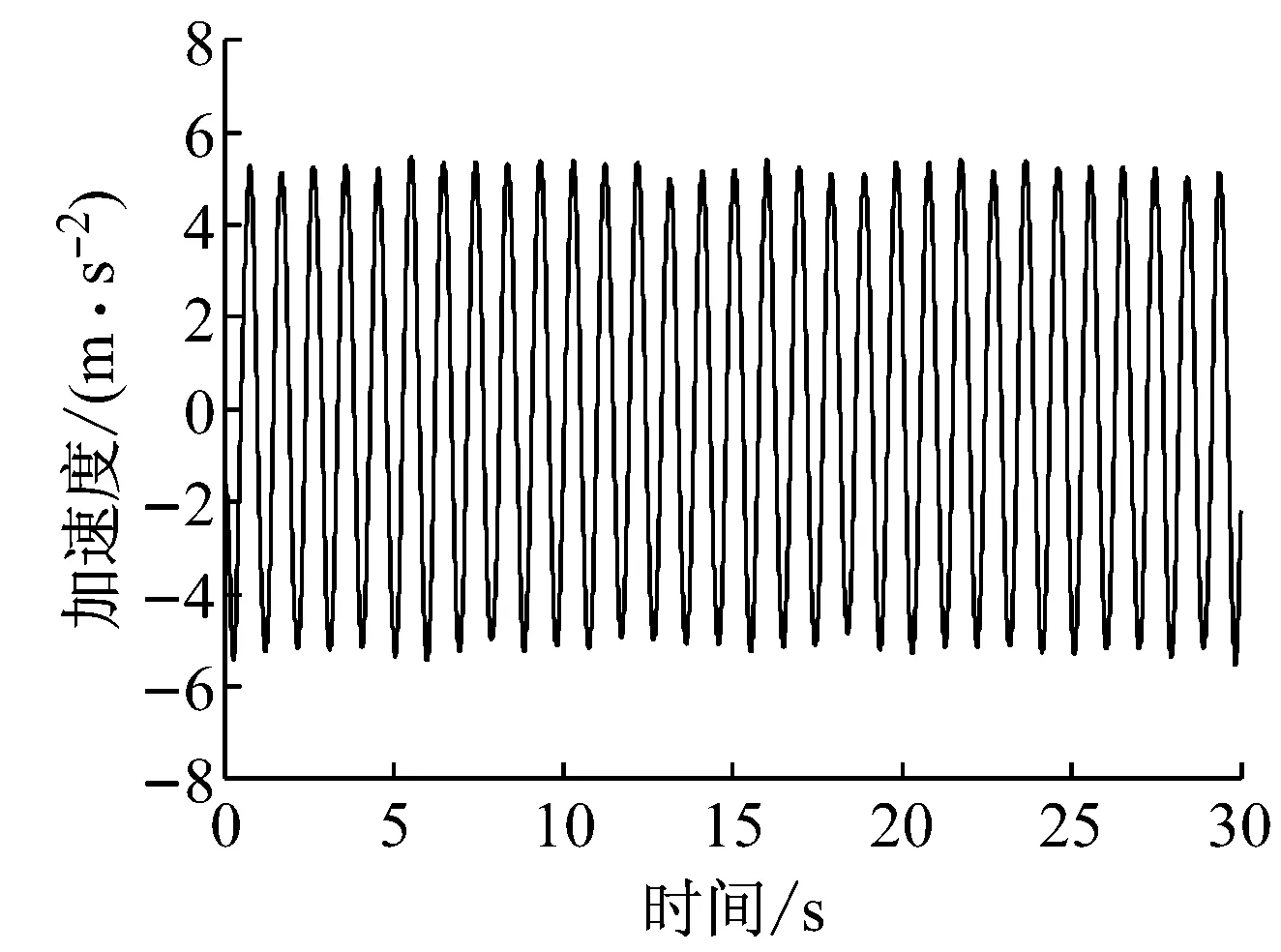
a 无降雨时加速度时程

b 无降雨时功率谱密度
图5 10 mm·h-1雨强下拉索加速度时程与功率谱密度(U=9 m·s-1,ξ=0.1%)
Fig.5 Time-history and PSD curves of acceleration with rainfall intensity 10 mm·h-1(U=9 m·s-1,ξ=0.1%)
由试验可知,对于不同的雨强,拉索有不同的振动风速区间,并有不同的振动幅值.拉索振动对雨强十分敏感,仅在特定的雨强区间发生振动,过大的雨强会抑制拉索风雨激振,各风速下拉索振幅最大值均在10 mm·h-1或20 mm·h-1雨强处取得.
对于拉索表面水线的形式,试验时观测发现,当风速达到7 m·s-1以上时,拉索下表面存在有稳定的水线,拉索上表面形成能明显观测到的上水线,但此时并非所有拉索发生风雨激振,风雨激振现象仅在上水线发生振荡时发生,其余状况下,上水线保持稳定的存在,但拉索并未发生风雨激振现象.

图6 不同雨强下拉索振幅随风速变化

图7 不同风速拉索振幅随雨强变化
通过阻尼圈调节结构阻尼,探究机械阻尼措施对拉索风雨激振现象抑制作用的有效性.图8给出在20 mm·h-1雨强下不同阻尼比时拉索振幅随风速变化规律.当阻尼比提高到0.50%时,风雨激振现象完全消失.由此可知,增加机械阻尼对于抑制拉索风雨激振有着十分显著的效果.

图8 不同阻尼比拉索振幅随风速变化
螺旋线被认为是抑制拉索发生风雨激振最有效的措施,对于3种螺旋线高度拉索模型,在所有风速、雨强的组合中均未发生大幅风雨激振.图9给出3种螺旋线索在8,20 mm·h-1雨强下振幅随风速变化.说明了螺旋线能有效的抑制拉索风雨激振,拉索1.5 mm高螺旋线已足够抑制其风雨激振现象.

图9 20 mm·h-1雨强拉索振幅随风速变化
2.2 Φ200拉索风雨激振试验
对于直径200 mm的光索模型,文献[23]给出在α=25°,30°且β=25°,30°,35°组合情况下斜拉索易发生雨振,其中心发振风速约为12 m·s-1,雨量为小雨甚至毛毛雨.由于试验条件原因,并没有再重现200 mm拉索模型在12 m·s-1风速下的风雨激振现象,而是当拉索处在倾角α=25°,风偏角β=25°的空间姿态时,在2 m·s-1风速下发生了大幅振动,且有雨和无雨时均发生振动,有雨时振幅较无雨时大.图10和图11分别给出2 m·s-1风速下,直径200 mm拉索在无雨时以及60 mm·h-1降雨下振动加速度时程和频谱图.
图12和图13分别给出直径200 mm光索在不同雨强下振幅随风速变化和在不同风速下振幅随雨强变化.由试验结果可知,拉索在2 m·s-1风速下发生振动,降雨后振幅增大,当雨强增大至超过70 mm·h-1后,振幅减小.整个低风速试验中,并没有发现拉索表面有成形的上水线,仅在表面附着水膜,且没有明显振荡现象.
螺旋线对拉索风雨激振的抑制效果如图14所示.两种高度螺旋线拉索结果相似,在降雨条件下,拉索振动被大幅度抑制.但在整个试验过程中,不论降雨与否,拉索模型均存在与光索在无降雨条件下振动幅值相似的振动.
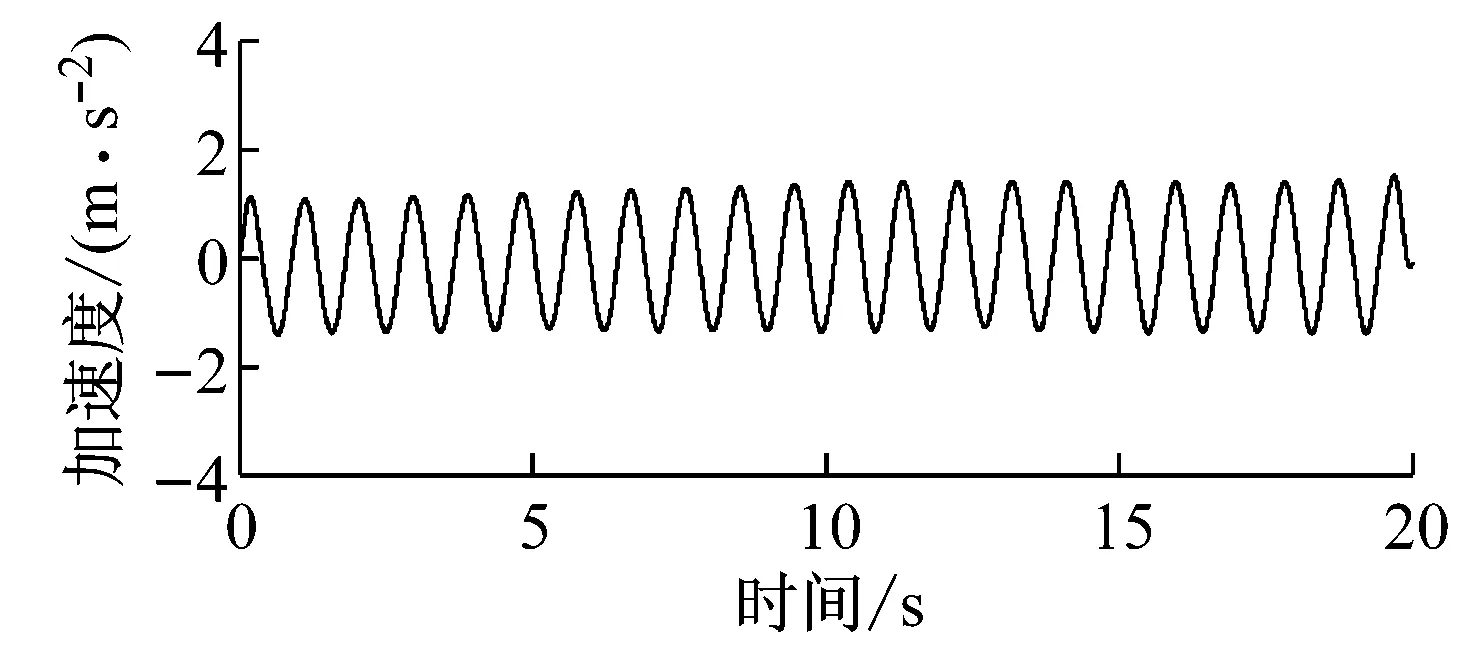
a无降雨时加速度时程

b无降雨时功率谱密度

a加速度时程

b功率谱密度
由于光索在风速2 m·s-1时发生大幅振动,对1~3 m·s-1风速区间内的风速,以0.5 m·s-1为风速变化步长,增加试验工况,得到2 m·s-1风速附近振幅随雨强的变化,如图15所示.由试验结果可知,风速在1.5、2、2.5 m·s-1时,干索均发生大幅振动.在2 m·s-1时,降雨时的拉索振幅明显大于无雨时的振幅,在雨强范围20 mm·h-1~60 mm·h-1时保持稳定的大幅振动.在1.5 m·s-1以及2.5 m·s-1时,降雨条件下拉索振幅波动较大,但振幅均小于2 m·s-1风速时拉索在降雨条件下的稳定大幅振动.
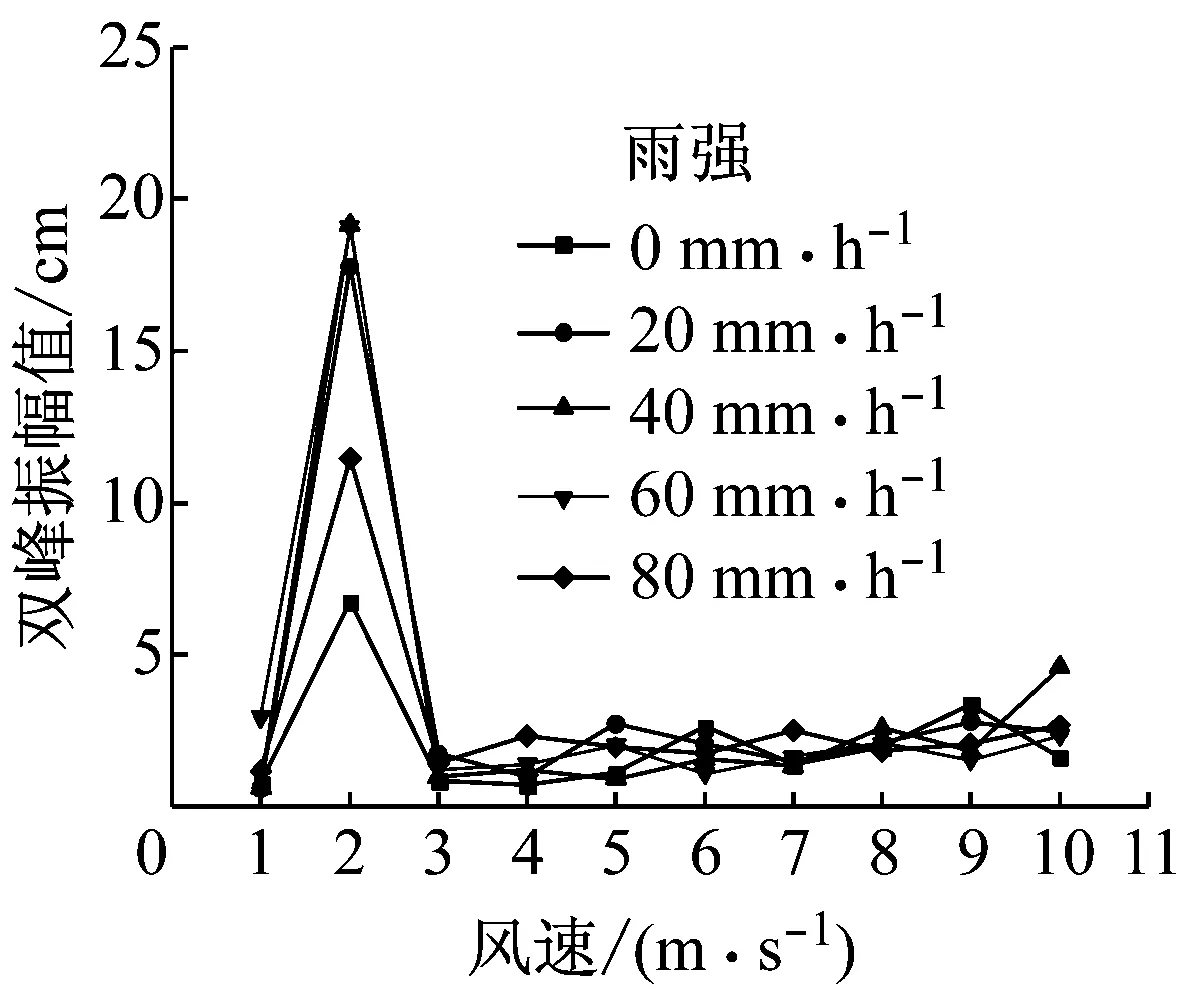
图12 不同雨强下振幅随风速变化图

图13 不同风速下振幅随雨强变化

图14 2 m·s-1风速下螺旋线振幅随雨强变化

图15 2 m·s-1风速附近振幅随雨强变化
3 机理分析
试验中两种不同直径(139 mm,200 mm)的拉索都发生了大幅振动,但发生振动的条件以及现象有所不同.139 mm的拉索在风速8 m·s-1、雨强为20 mm·h-1时振幅最大,且拉索表面有稳定振荡的上水线存在,在无雨时不发生振动.200 mm的拉索在风速为2 m·s-1时首先在无降雨条件下发生振动,进而在降雨的影响下振幅增大,且没有成形的振荡的上水线.139 mm的拉索的最大振幅大于200 mm拉索的振幅.根据许林汕[13]的试验研究,同一根拉索也会在不同的风雨条件下发生振动,且高风速小雨量时的振幅大于低风速大雨量时的振幅.因此,拉索在不同风速下发生大幅振动的成因可能会有差异.
Matsumoto[16]等人发现即使在无雨天气下,斜拉桥拉索也会发生不同于普通驰振和抖振的大幅度振动现象,通过风洞试验提出了轴向流理论.他认为激发拉索风雨激振的两个因素(上水线以及轴向流)可以独立的起作用.之后,Matsumoto提出了高风速涡致振动理论[17]和卡门涡抑制理论[19]来进一步解释拉索在无雨和有雨条件下的大幅振动,认为轴向流会和尾流相互作用,缓和卡门涡的脱落,导致拉索的气动不稳定性,且合适位置的水线会加剧该种涡致振动.
139 mm的光索在8 m·s-1风速下(折算风速U/fvD=57.55发生的大幅振动,且带有螺旋线的拉索在相同条件下不再发生振动,说明拉索的风雨激振和水线有关.多数研究结果均表明[14-15,21-23],水线和拉索的耦合运动会引发拉索准驰振限幅运动.因此,试验中139 mm的拉索振动很可能是驰振驱使的.
200 mm光索为圆柱截面,圆柱涡激振动的起振风速由Strouhal数(St=fvD/U)决定.对于该拉索模型,涡激振动的中心风速为1 m·s-1.然而在1 m·s-1时拉索并未发生大幅振动.风速在1.5,2.0,2.5 m·s-1时,干索均发生大幅振动.原因之一为是拉索发生了涡激振动,1 m·s-1风速太小,能量不足以使拉索发生大幅振动;另外一种可能是拉索受到了轴向流的影响.在降雨条件下,拉索在2 m·s-1的风速下(折算风速U/fvD=10)振幅增大.根据文献[24]可知,降雨对圆柱模型的涡振具有抑制作用.在实验中,降雨不仅没有使拉索振幅减小,反而增大了拉索振幅,因此不是传统意义上的涡激振动.
在2 m·s-1时,由Strouhal数可知卡门涡的频率为2 Hz.根据Matsumoto的卡门涡与轴向流的相互作用理论[18],如果实验中每两个卡门涡从拉索上脱落时,有一个轴向涡脱落,那么尾流中的1 Hz的频率会被加强,这将导致固有频率为1 Hz的拉索发生大幅振动,该假设示意图见图16.并且根据文献[20],均匀风场中索面没有水线和有水线的情况下轴向流强度的强度会有所不同,即索表面状态可能会影响轴向流的强度,这可能是适当的降雨条件下拉索振幅增大的原因之一.因此,200 mm拉索在无雨时和有雨时的大幅振动与轴向流和水线都有关系,是一种与准驰振不同的涡致振动.在加入抑制措施后,拉索的振动得到一定程度的抑制,但拉索模型均存在与光索在无降雨条件下振动幅值相似的振动,如图14所示.由此可以说明,利用螺旋线破坏拉索表面原有的状态,可以抑制水线对拉索振动的加剧作用.

图16 轴向流与卡门涡街示意图
综上所述,对于不同折算风速下的拉索振动,机理可能存在差异.对于139 mm直径的拉索,在8 m·s-1的风速下的振动是准驰振类型的限幅振动.200 mm拉索在2 m·s-1风速下的风雨激振现象是由轴向流和表面水线共同导致的,是一种涡致振动.具体的作用机理以及细节分析还需要进一步的研究确定.对于139 mm的拉索,螺旋线能够完全抑制拉索的大幅振动,而对于200 mm的拉索,螺旋线对拉索振动的抑制作用有限.因此在实际工程中,需要明确拉索大幅振动的机理,运用更合适的措施来防止拉索的大幅振动.
4 结论
利用高精度人工降雨装置,在风洞中成功再现了直径为139 mm以及200 mm拉索的风雨激振现象,并螺旋线抑制拉索风雨激振的有效性.通过一系列拉索模型的人工降雨试验,对比分析试验结果,可得到如下结论:
(1)拉索模型只在最不利空间姿态下发生大幅风雨激振,并且对风速和雨强敏感,存在使拉索发生最大振幅的风速与雨强的组合.
(2)阻尼比对拉索风雨激振有较大的影响.总体来说,阻尼比越大,拉索振幅越小,振动区间越小,当阻尼比达到一定值时,拉索风雨激振现象消失.
(3)对于不同折算风速下拉索发生大幅振动的原因可能有所差异.在高风速下,拉索的振动更类似限幅的准驰振振动;在低风速下拉索的振动与涡致振动的关系更密切.
(4)螺旋线对于抑制风雨激振具有十分良好的效果.对于139 mm的拉索,1.5 mm的螺旋线可以完全抑制拉索的风雨激振.对于200 mm的拉索,螺旋线可以减小拉索在有雨条件下的振幅,但不能完全抑制拉索的振动,即螺旋线不能减弱轴向流的影响.因此在实际工程中,仍要根据拉索的振动形式运用合理的抑振措施.
[1] Hikami Y, Shiraishi N. Rain-wind induced vibrations of cables stayed bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1988, 29(1): 409.
[2] Yamaguchi K, Manabe Y, Sasaki N,etal. Field observation and vibration test of the Tatara Bridge[C]∥Proceedings of the IABSE Conference, Cable-Stayed Bridges, Past, Present, and Future.[S.l.]: IABSE, 1999: 707-714.
[3] Matsumoto M, Shirato H, Yagi T,etal. Field observation of the full-scale wind-induced cable vibration[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(1): 13.
[4] Flamand O. Rain-wind induced vibration of cables[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 57(2): 353.
[5] Bosdogianni A, Olivari D. Wind-and rain-induced oscillations of cable of stayed bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1996, 64: 171.
[6] Matsumoto M, Saitoh T, Kitazawa M,etal. Response characteristics of rain-wind induced vibration of stay-cables of cable-stayed bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 57(2): 323.
[7] 顾明, 杜晓庆. 带人工雨线的斜拉桥拉索模型测压试验研究[J]. 空气动力学学报, 2005, 23(4): 419.
GU Ming, DU Xiaoqing. Testing study on wind pressure distributions of stayed cables with an artificial rivulet[J].ActaAerodynamicaSinica, 2005, 23(4): 419.
[8] LIU Qingkuan. Study on the mechanism of rain-wind induced vibration of cables on cable-stayed bridge using LES[J]. Engineering Mechanics, 2007, 24(9): 134.
[9] Rocchi D, Zasso A. Vortex shedding from a circular cylinder in a smooth and wired configuration: comparison between 3D LES simulation and experimental analysis[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90:475.
[10] 李寿英, 顾明. 带固定人工水线三维拉索绕流的数值模拟[J]. 同济大学学报:自然科学版, 2005, 33(5):590.
LI Shouying, GU Ming. Numerical simulation of flow around stay cables with artificial rivulet[J]. Journal of Tongji University: Natural Science, 2005, 33(5):590.
[11] 顾明, 李寿英, 杜晓庆. 斜拉桥拉索风雨激振理论模型和机理研究[J]. 空气动力学学报, 2007, 25(2): 169.
GU Ming, LI Shouying, DU Xiaoqing. Testing study on wind pressure distributions of stayed cables with a fixed artificial rivulet[J]. Acta Aerodynamica Sinica, 2007, 25(2): 169.
[12] 陈文礼. 拉索风雨激振的试验研究与数值模拟[D]. 哈尔滨:哈尔滨工业大学, 2009.
CHEN Wenli. Experimental study and numerical simulation of rain-wind induced vibration of stay cables[D]. Harbin: Harbin Institute of Technology, 2009.
[13] 许林汕, 葛耀君, 赵林. 高精度风雨模拟环境下拉索风雨激振试验研究新发现[J]. 土木工程学报, 2011, 44(5): 86.
XU Linshan, GE Yaojun, ZHAO Lin. Experimental study of rain and wind induced vibration of stay cables using high precision rain simulation system[J]. China Civil Engineering, 2011, 44(5): 86.
[14] 李寿英, 陈政清, 顾明. 拉索风雨激振中拉索和水线之间的耦合运动[J]. 振动与冲击, 2008, 27(10):1.
LI Shouying, CHEN Zhengqing, GU Ming. Coupled motion between stay cables and rivulets in rain-wind induced vibration [J].Journal of Vibration and Shock, 2008, 27(10):1.
[15] 李永乐, 徐幼麟, 沈其民, 等. 斜拉桥拉索风-雨致振动(Ⅰ) :机理分析[J]. 西南交通大学学报, 2011, 46(4):529.
LI Yongle,XU Youlin, SHEN Qimin,etal. Rain-wind-induced vibration of cables in cable-stayed bridges (Ⅰ): mechanism analysis[J]. Journal of Southwest Jiaotong University, 2011, 46(4):529.
[16] Matsumoto M, N Shiraishi, H Shirato. Rain-wind induced vibration of cables of cable-stayed bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 41/44: 2011.
[17] Matsumoto M, Yagi T, Goto M,etal.Rain-wind-induced vibration of inclined cables at limited high reduced wind velocity region[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91: 1.
[18] Matsumoto M, Yagi T, Shigemurab Y,etal. Vortex-induced cable vibration of cable-stayedbridges at high reduced wind velocity[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89: 633.
[19] Matsumoto M, Yagi T, Oishi T,etal. Motion effect of water rivulet on rain-wind induced vibration of inclined stay-cables[C]∥Proceeding of Sixth Internation Symposium on Cable Dynamics. Charleston: [s.n.], 2005: 255-262.
[20] 刘庆宽, 张峰, 乔富贵. 轴向流对斜拉索气动稳定性影响的试验研究[J]. 石家庄铁道学院学报:自然科学版,2008,21(4): 16.
LIU Qingkuan, ZHANG Feng, QIAO Fugui. Effect of axial flow on rain-wind induced vibration of stay-cables[J]. Journal of Shijiazhuang Railway Institute: Natural Science, 2008,21(4): 16.
[21] 顾明, 黄麟, 王国砚. 水线震荡对斜拉桥拉索风雨激振稳定性的作用[J]. 振动工程学报,2004, 17(1): 96.
GU Ming, HUANG Lin, WANG Guoyan. Effects of motion of rivulet on stability of rain-wind induced vibration of cables of cable-stayed bridges[J]. Journal of Vibration Engineering, 2004, 17(1): 96.
[22] 李永乐, 卢伟, 陶齐宇,等. 斜拉桥拉索风雨致振动特性风洞试验研究[J]. 实验流体力学, 2007, 21(4): 36.
LI Yongle, LU Wei, TAO Qiyu,etal. Study on rain-wind induced vibration of cables in cable-stayed bridges by wind tunnel test[J]. Journal of Experiments in Fluid Mechanics, 2007, 21(4): 36.
[23] Zhan S, Xu Y L, Zhou H J,etal. Experimental study of wind-rain-induced cable vibration using a new model setup scheme[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96: 2438.
[24] 赵林, 葛耀君, 武占科, 等. 风雨耦合环境结构荷载与响应的分析及试验研究[J]. 振动工程学报,2014, 27(4): 507.
ZHAO Lin, GE Yaojun, WU Zhanke,etal. Theoretic and testing investigation of wind-rain coupling loads on bridges and structures[J]. Journal of Vibration Engineering, 2014, 27(4): 507.
Experimental Study on Aaerodynamic Stability of Rain-wind Induced Vibration of Stay Cables of Different Diameters
CHANG Ying, LUO Wei, ZHAO Lin, GE Yaojun
(State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)
Rain-wind induced vibration of cables is a type of vibration with large amplitude and low frequency. The phenomenon of rain-wind induced vibration of cables of two different diameters is successfully re-produced under simulated raining condition through wind tunnel test. The effects of several main factors on the characteristics of rain-wind vibration and spiraled wires countermeasure for mitigation of the vibration are investigated. The results indicate that the mechanism of vibrations with different reduced velocities is different. Vibration with high reduced velocity is more like a type of galloping, while vibration with low reduced velocity is more related to vortex-induced vibration.
cables; rain-wind induced vibration; artificial rainfall test; spiraled wires
2015-11-18
国家“九七三”重点基础研究发展计划(2013CB036300);交通运输部应用基础研究(2013319822070);国家自然科学基金(91215302,51178353,51222809);新世纪优秀人才支持计划.
常 颖(1991—),女,博士生,主要研究方向为桥梁抗风.E-mail:changying@tongji.edu.cn
葛耀君(1958—),男,教授,博士生导师,工学博士,主要研究方向为桥梁抗风.E-mail:yaojunge@tongji.edu.cn
U448.27
A
