压气储能洞室气密性影响因素分析

叶 斌， 程子睿， 彭益成

(1.同济大学 土木工程学院，上海 200092； 2.上海电力设计院有限公司，上海 200025)



压气储能洞室气密性影响因素分析

叶 斌1， 程子睿1， 彭益成2

(1.同济大学 土木工程学院，上海 200092； 2.上海电力设计院有限公司，上海 200025)

压缩空气储能技术可以解决可再生能源发电的不稳定性和间歇性的缺点，而地下储气洞室是压气储能工程的重要组成部分.人工开挖并施作内衬的硬岩洞室因受地质条件限制小、适应范围广、气密性和稳定性好而受到关注.研究了内衬混凝土渗透率对洞室气密性的影响，基于达西定律，推导了计算储气洞室气体泄漏量的理论公式，获得了典型压缩空气储能压力条件下洞室内部气体的泄漏情况，并在此基础上分析了衬砌渗透率、衬砌厚度和洞室形状三种因素对气密性的影响.结果表明，在洞室内压8 MPa的情况下，利用P8等级的抗渗混凝土作为混凝土内衬，可以使洞室内气体日泄漏量低于1%，满足压缩空气储能电站的运行要求.同时，气体泄漏量随着内衬渗透率的增加而线性增加；在相同的渗透率条件下气体泄漏量随衬砌厚度的增加而减小；在相同容积条件下，圆柱形地下储气库的密封效果好于球形洞室.研究结果证明内衬硬岩洞室作为压缩空气的地下储气库在理论上具有良好的可行性.

压缩空气储能； 内衬硬岩洞室； 气体泄漏； 解析计算

随着可持续发展战略的推行以及工业技术的发展，风能、太阳能等新能源发电技术发展迅速，对于缓解全球气候变暖、防治环境污染起到了重要作用.然而可再生能源的发电量受到自然条件的限制，具有不稳定性和间歇性的缺点[1].电力储能技术通过一定介质存储电能，在需要时将所存能量释放发电，可以克服可再生能源的间歇性特点，形成稳定的电力供应向用户按需、持续供电[2].压缩空气储能系统(Compressed Air Energy Storage，CAES)是一种能够实现大容量和长时间电能存储的电力储能系统.在用电低谷时，用电网中多余的电能驱动空气压缩机，把空气压缩进地下洞室储存起来，到用电高峰时，再把高压空气放出，并与少量的气体燃料混合在气轮机燃烧室中燃烧而迅速膨胀做功，进而带动发电机发电[3].地下储气库作为压缩空气储能电站主要组成部分，是保障其运行性能和可靠性的技术关键.可用于压缩空气储能地下储气库的地质构造可以分为三大类：①人工溶蚀的盐岩溶腔;②含水层中的多孔介质岩石;③硬岩中人工开挖的地下洞室[4].由于前两种方式需要比较特殊的地质构造，因此在一些风力资源丰富的地区，在硬岩中人工开挖的地下洞室便成为最有可能采用的地下储气库方案.

在硬岩中建设储气库，由于天然岩石中不可避免的存在着节理裂隙，会极大影响储气库的气密性，降低储气库的运行效率，因此通常需要采用工程措施来保证储气洞室的气密性.在硬岩洞室内施作内衬，通过增加一层人工屏障来保证洞室的气密性，是一种较为可行的地下储气洞室方案.

目前，瑞典已经采用内衬洞室的形式建成了一个天然气储气库，证实了硬岩中人工开挖的地下洞室作为地下储气库的可行性[5].美国Norton Energy Storage LLC公司正在计划利用地下废弃的石灰岩矿洞作为储气库，建立2 700 MW的压气储能电站[6].美国Iowa地区计划建设一个采用多孔介质岩石作为储气库的压气储能电站[7].此外，美国还计划在中部五大湖附近建设一个采用水封式不内衬硬岩洞室作为储气库的压气储能电站[8].韩国正在研究利用内衬硬岩洞室建设压气储能电站的可能性[9-10].我国也在研究硬岩洞室作为储气库的可行性[11-12].

对于压缩空气储能电站地下储气库的气体泄漏情况分析，Allen[13]等研究了储气库泄漏情况对压气储能电站运行效率的影响，认为为了保证压气储能电站的运行效率，储气库每天的空气泄漏量应小于1%.Kim[9-10]等研究了内衬岩洞中气体泄漏情况，认为储气压力在5～8 MPa之间，混凝土衬砌的渗透率低于1×10-18m2时，可以使得每天的泄漏率低于1%.Zhuang[14]等分析了无内衬硬岩洞室中气体的泄漏情况，结果表明不使用内衬的情况下，每天的气体泄漏情况远远超过压气储能电站要求的1%，因此无内衬硬岩洞室不适合作为储气洞室.陈卫忠[15]等研究了含夹层盐穴储气库运行过程中气体的渗透规律，建立了含软弱夹层盐岩储气库的等效边界气体渗流模型，该模型可反映夹层层面流的问题，可用于含夹层盐穴储气库运行过程中气体渗透规律的研究.钟巍[16]等研究了内含空腔围岩中气体渗流动力学问题.但总体而言，国内外目前对于压缩空气储能内衬洞室中空气泄漏情况的研究还非常有限.

针对使用混凝土内衬的硬岩洞室，通过理论分析，得出内衬硬岩洞室中空气泄漏量随洞室内部压力变化的计算公式，并且利用此计算公式，计算典型的压缩空气储能条件下的空气泄漏量，并且分析了各种参数对空气泄漏量的影响.计算结果表明，内衬硬岩洞室作为地下储气库在理论上是可行的.

1 洞室中空气泄漏量计算的理论公式

为方便推导和研究，取储气工程中常用的球形洞室作为研究对象，即在球形储气洞室内部用一圈混凝土进行内衬，洞室截面如图1所示，且混凝土介质各向均匀，即混凝土中孔隙也是均匀分布，于是可以取某一方向上空气渗流情况进行分析.假设开挖洞室的半径为r，储气空间的半径为r0，混凝土的厚度为r-r0，初始情况洞室内部与外界的压力差为Δp0.由于周围的内衬混凝土中存在孔隙，在压力差的作用下，洞室内部的气体就会缓慢地向混凝土内渗透.随着空气渗出，洞室内部与外界的压力差逐渐减小，当压力差减小至0，渗流现象随即停止.

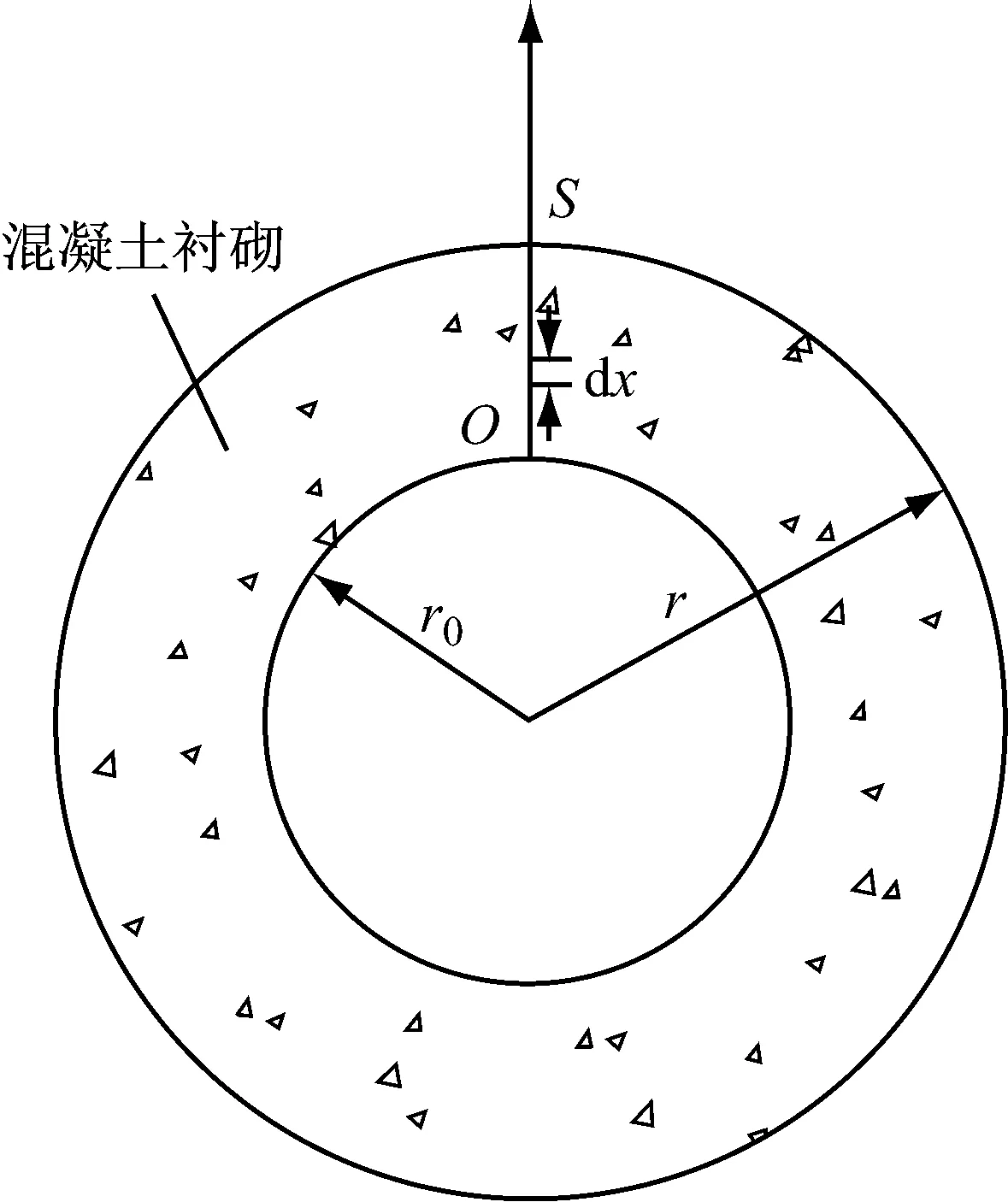
图1 洞室截面示意图

令洞室边缘的某点O为坐标原点，根据达西定律，压力差取正值，对于不同渗流距离的渗流速度u为[16]

(1)

式中：Δp为洞室内部与混凝土内x位置的压力差;Δx为渗透距离;μ为空气动力粘度;k为渗透率，取洞室边缘为坐标原点，式(1)可简化为

(2)

随着气体的不断渗流，压力差Δp也不断变化，根据理想气体状态方程

pV=nRT

(3)

式中：p为理想气体的压强；V为理想气体的体积；n为气体物质的量；R为理想气体常数；T为理想气体的温度.根据式(3)，可以计算当气体渗入混凝土内x位置时，洞室内部与混凝土外部压力差Δpx为

(4)

式中:Δp0为初始情况下洞室与混凝土外部的压力差;Vm为当前温度条件下的气体摩尔体积;ΔVx为此时已经渗入到混凝土中的气体体积；Vcavern为储气洞室的体积.

虽然在气体渗流的过程中，随着压力的变化，气体温度也会产生相应的变化，但是考虑到气体的渗流速度很慢，温度的变化非常小，因此在公式的推导过程中忽略了温度变化对气体压力和体积的影响.

渗流开始后，设气体到达混凝土外表面之后才属于气体泄漏，假设气体到达S点时，渗出气体的渗流速度为uA(t)，计算时取混凝土外表面为气体渗出的表面，以r表示混凝土内衬的半径，r0为储气洞室的半径，那么在dt时间内泄漏的气体体积为

dV=uA(t)·dt·4πr2

(5)

对于混凝土内衬，有

(6)

式中:η为孔隙率；Vpore为可容纳空气的孔隙体积.

因为一般混凝土的孔隙较少，孔隙中的气体可以忽略，因此取气体刚刚渗流到S点时为时间起点，并且时刻t渗出的气体体积为ΔV(t)，于是此时洞室内部与混凝土外部的压力差为

(7)

对式(5)进行积分得

(8)

令

(9)

则

(10)

解微分方程可得泄漏的气体体积随时间的表达式，单位为m3.

(11)

若洞室内部初始气压为p0，标准大气压为pair，则此时洞室内的气体在标准大气压下的体积为

(12)

气体渗流过程中洞室内部压力随时间变化趋势可以表示为

(13)

根据式(11)与式(13)，把典型的压气储能电站运行参数代入，便可以计算得到储气洞室的气体泄漏情况.

2 算例分析

将模拟一种压缩空气储能洞室在典型工作条件下的气体泄漏情况.假设洞室直径10 m，内衬混凝土的厚度为0.5 m，洞室位于地下100 m深处，洞室内温度为23 ℃(296.15 K)，混凝土的孔隙率η为1%，各参数取值如下：xA=0.5 m，μ=1.8×10-5Pa·s，R=8.314，T=296.15 K，Vm=0.024 5 m3·mol-1，p0=8 MPa，r=5.5 m，r0=5 m，η=1%.

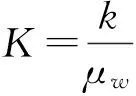
表1 渗透标号与渗透率换算

如果k取P8级抗渗混凝土的渗透率，即k=2.380×10-18m2.计算结果如图2所示.由图2可以看出，洞室内的气体会在3 000 d左右泄漏完毕，泄漏的体积大约为41 400 m3，洞室内压力将降至接近0.同时，在开始泄漏的一段时间，泄漏量与时间大致呈线性关系.图3为24 h内气体泄漏量随时间的关系图.由图3可知，24 h内气体泄漏约69.42 m3，因此初始阶段气体泄漏速度大致为69.42 m3·d-1，即每天泄漏量大约是储气总量的0.17%.一般来说，压缩空气储能电站对地下储气库的要求是每天的气体泄漏率低于1%，因此模拟情况可以满足压缩空气储能电站的工作要求.

病情演变及预后状况 观察组肺挫伤程度评分（4.6±1.6）分、脱机时间 （8.1±2.1）d、ICU住院时间 （11.6±3.0）d、肺实变1例 （2%）、气管插管11例 （22%）、病死2例 （4%）。对照组肺挫伤程度评分 （5.8±1.8）分、脱机时间 （9.5±2.4）d、ICU住院时间 （13.5±2.7）d、肺实变8例 （16%）、气管插管13例 （26%）、病死4例 （8%）。观察组肺挫伤程度评分、脱机时间、ICU住院时间及肺实变率均低于对照组 （P ＜0．01或 P＜ 0．05）， 两组患者的气管插管率和病死率相比，差异无显著意义 （P ＞ 0．05）。

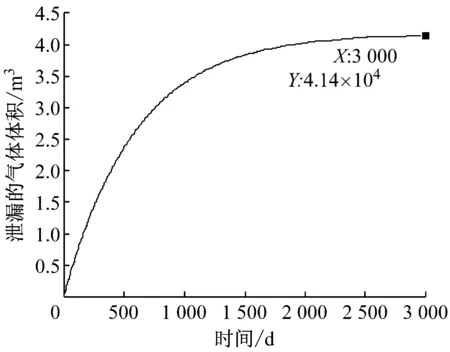
a 体积

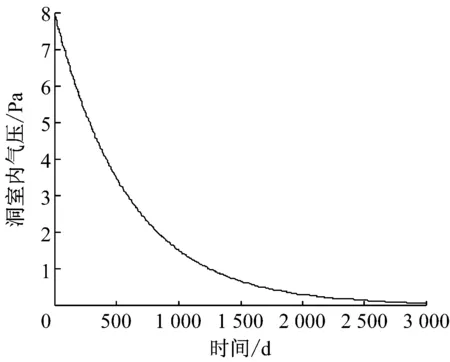
b 压力

按照所模拟的直径10 m的洞室来说，在这个洞室内储存的8 MPa压力的压缩气体，在标准大气压下体积为41 400 m3，1%的泄漏率为414 m3·d-1.通过反算可以得到，1%的泄漏率所对应的混凝土渗透率k=1.43×10-17m2，即当混凝土的渗透率k<1.43×10-17m2时，可以满足压缩空气储能电站的工作要求.

3 不同影响因素对气密性的影响

从以上的算例可以看出，渗透率对储气洞室的密封性有很大的影响，以下将具体分析渗透率对泄漏情况的影响以及其他参数的影响.

3.1 渗透率的影响

一般来说抗渗混凝土的最小渗透率是P12级的1.176×10-18m2，同时满足压气储能电站要求的最大渗透率是1.43×10-17m2，以下将通过计算各渗透率下气体全部泄漏所需要的时间以及每天的气体泄漏量，分析渗透率对泄漏情况的影响.

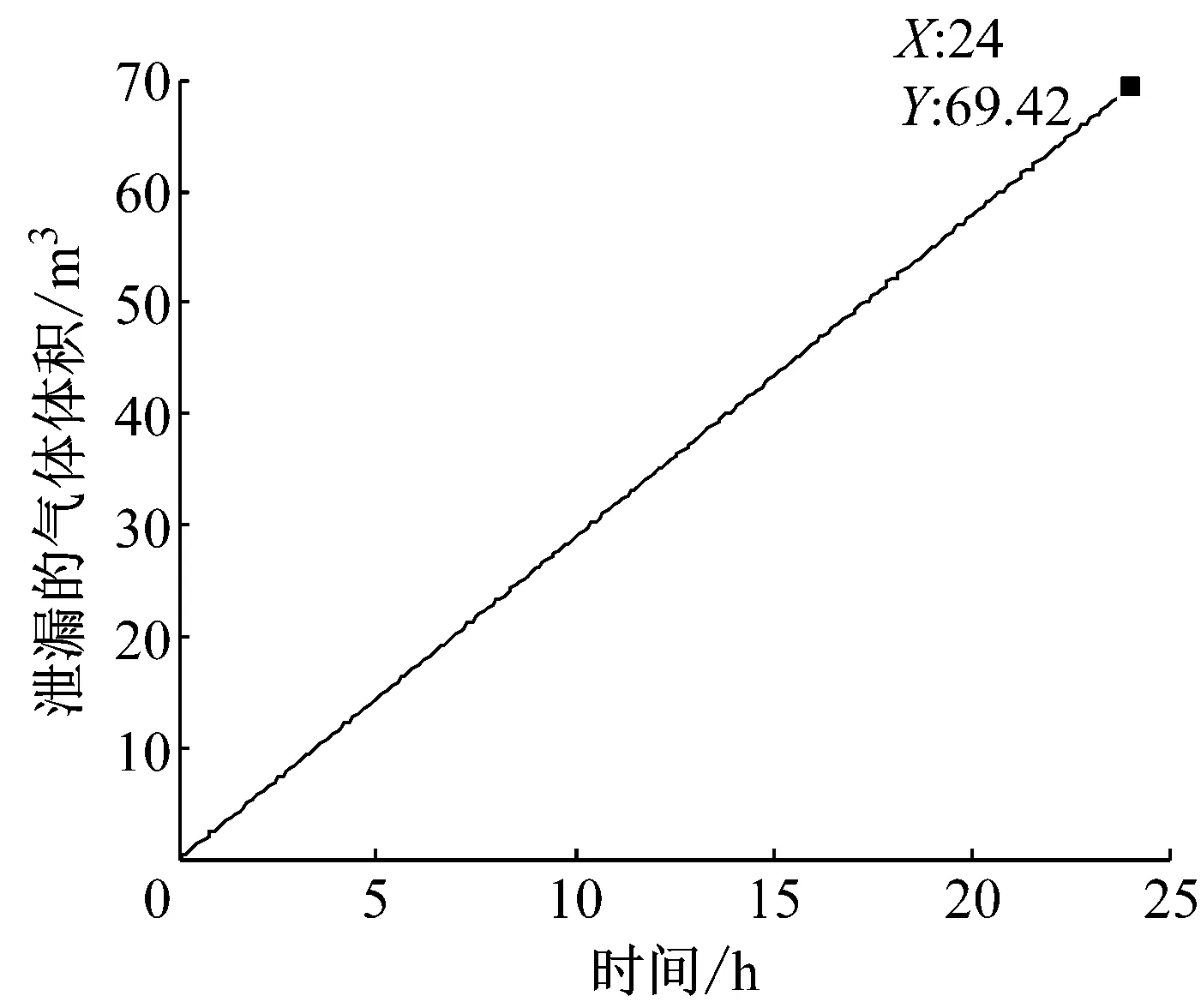
图3 24 h内气体泄漏量(k=2.380×10-18 m2)

通过计算可以看出,如图4所示，随着混凝土衬砌的渗透率从1.176×10-18m2增大到1.43×10-17m2的过程中，气体完全泄漏的时间不断减小，并且一开始的减小速度较快，随后减小的速度变慢，这说明渗透率在非常低的时候，对于气体的防渗效果非常好，而随着渗透率的增大，防渗效果会迅速变弱.由图5可以看出，随着渗透率的增加，每天的气体泄漏量基本上成线性增加.

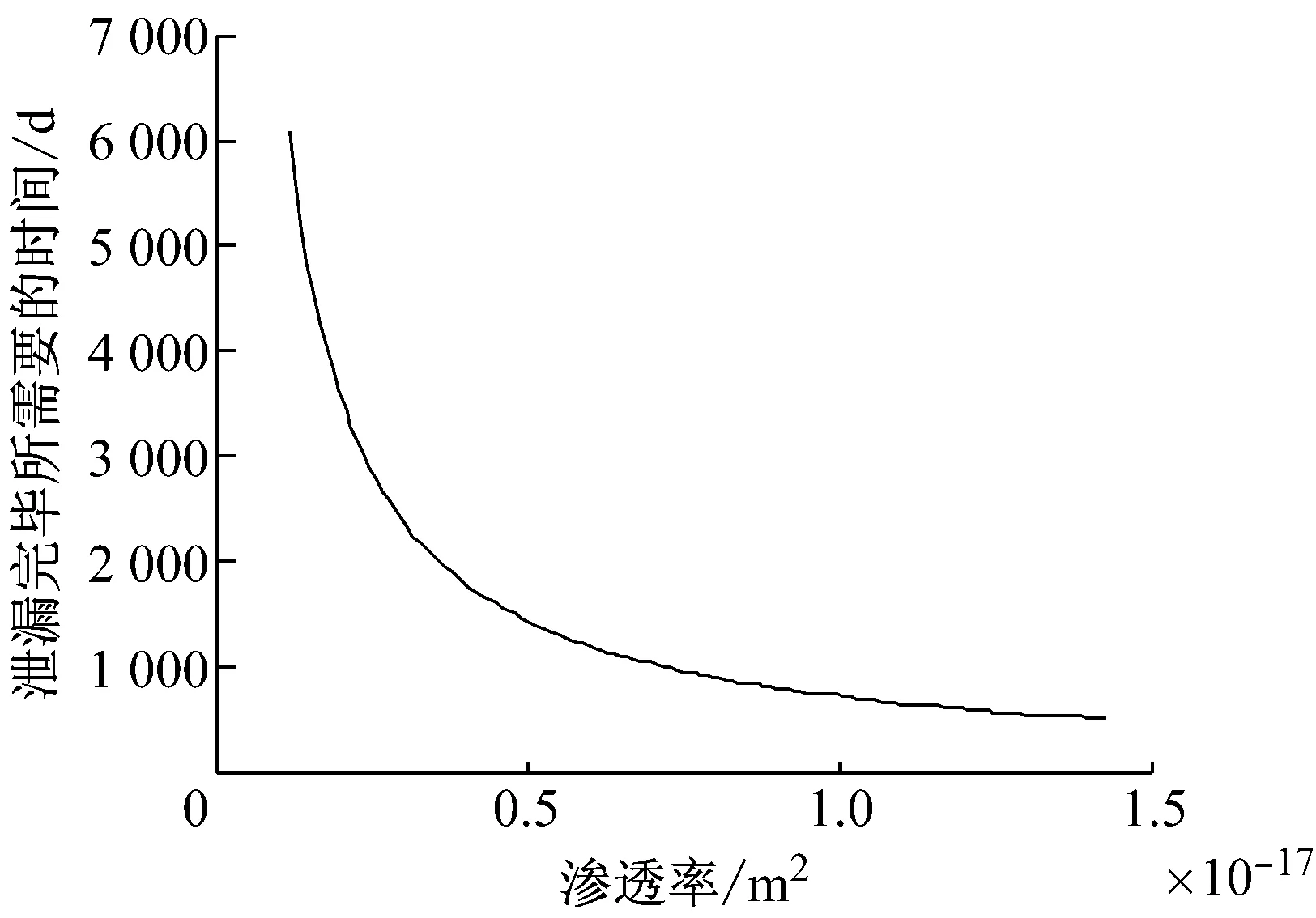
图4 不同渗透率下气体完全泄漏所需要的时间

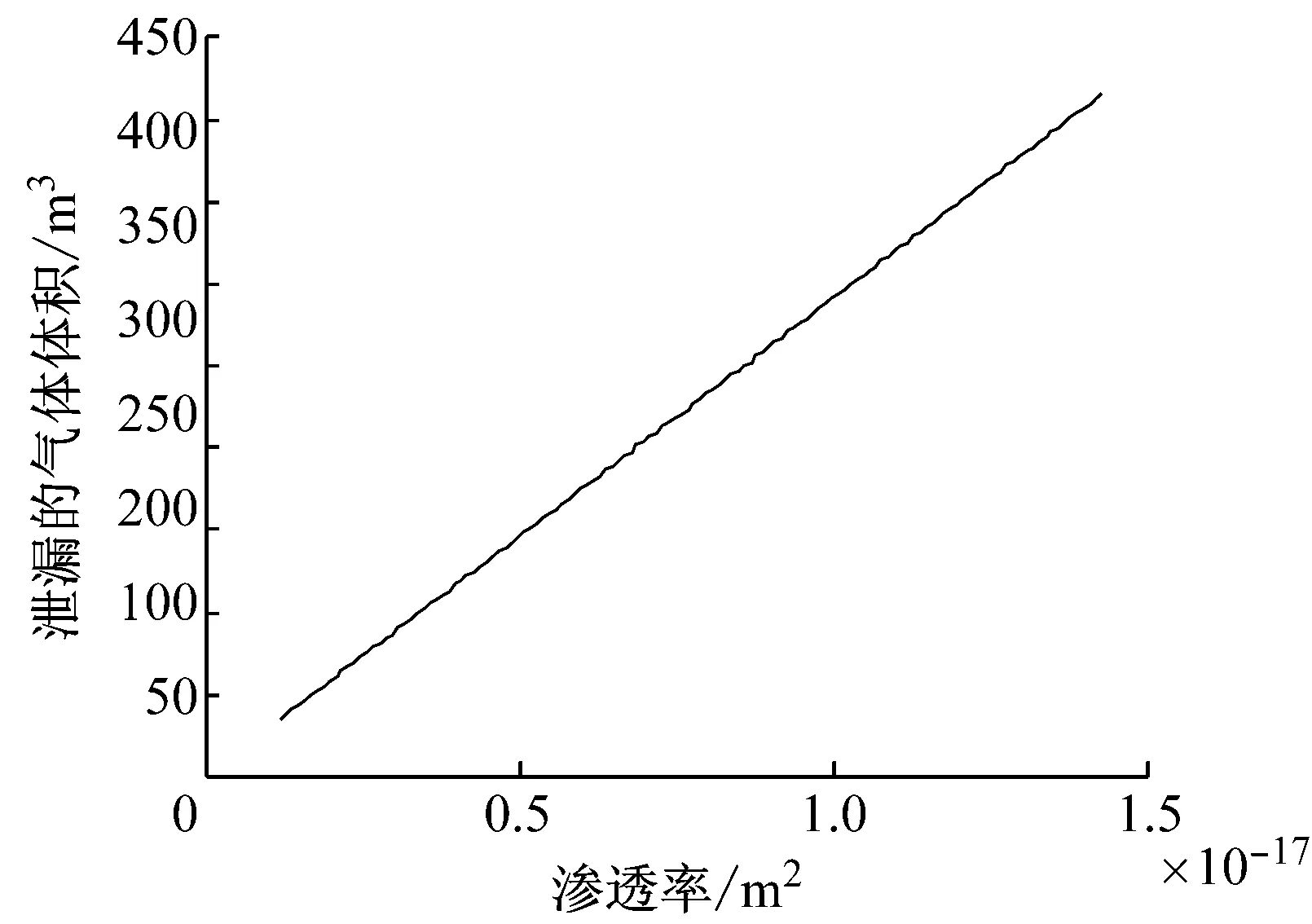
图5 不同渗透率下每天的气体泄漏量

3.2 衬砌厚度的影响

以上的分析都是基于0.5 m厚的衬砌厚度所进行的分析，以下将分析衬砌厚度对气体泄漏情况的影响.k取P8级抗渗混凝土，即k=2.380×10-18m2.

由图6可以看出，在衬砌厚度从0.5 m增加到1 m的过程中，每天的气体泄漏量由70 m3降低到35 m3左右.这说明随着衬砌厚度的增加，气体的泄漏量也在不断降低.但是在实际工程中，衬砌厚度的增加同样意味着需要开挖更大体积的洞室以及更多的抗渗混凝土，因此是否要通过增大衬砌厚度来保证抗渗效果还需要根据具体情况酌情考虑.

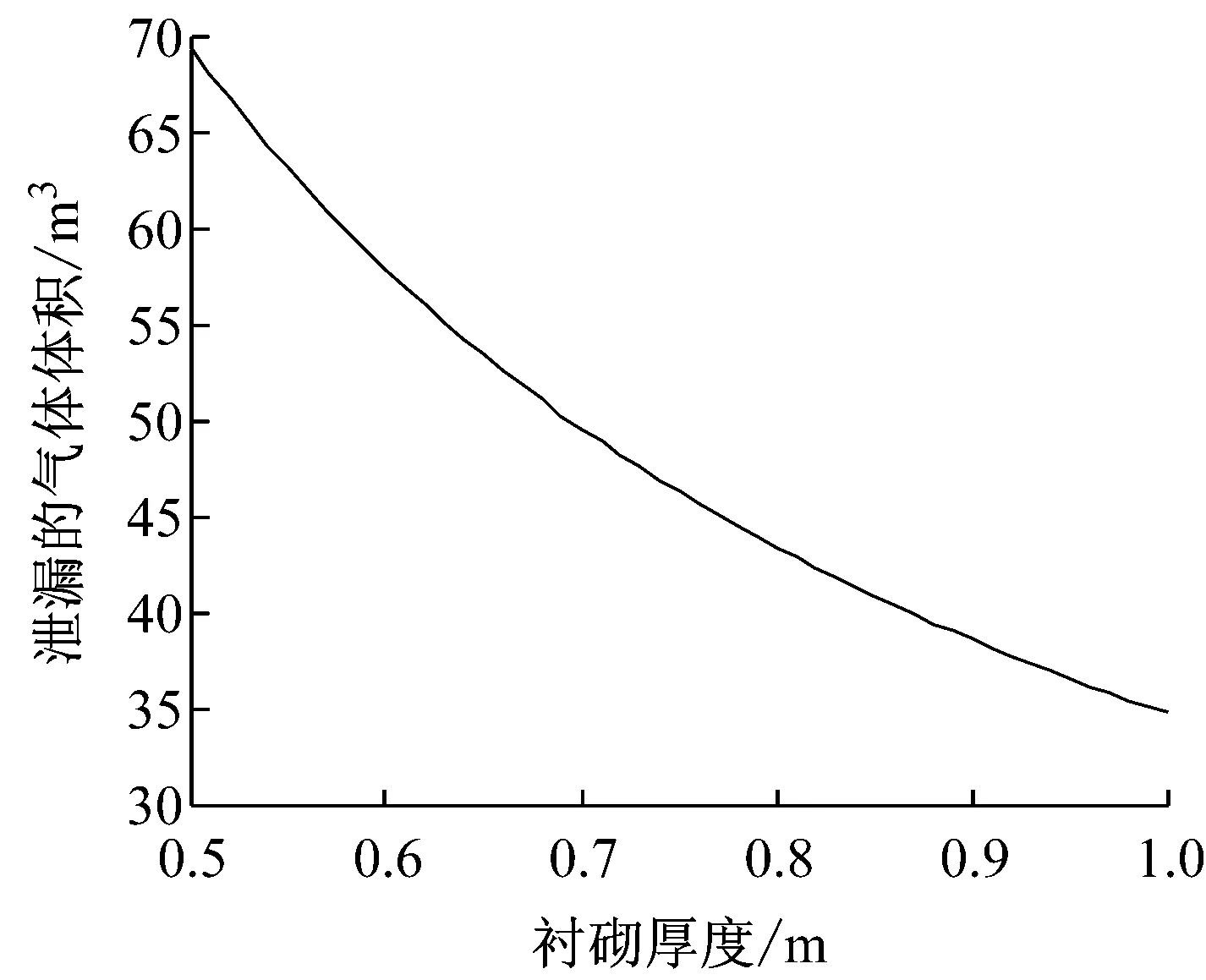
图6 不同衬砌厚度下每天的气体泄漏量

3.3 洞室形状的影响

以上的算例以及影响因素的分析均是基于球形洞室所做的分析，但是实际情况下，也会用到其他形状的储气洞室，因此需要研究洞室形状的影响.

一般来说，使用内衬洞室的压缩空气储能电站的地下储气库，另一种常用的形式为圆柱形隧道式储气库.如果采用圆柱形隧道来储存气体，并且与球体具有相同的直径与体积时，洞室是一个直径10 m，长6.67 m的圆柱形隧道.假设隧道两端是完全封闭的，气体只会从圆柱体的内壁向外泄漏，此时，式(5)就要改成

dV=uA(t)·dt·2πrl

(14)

式(6)变为

(15)

式中，l表示圆柱体长度.

同样，对式(14)进行积分，可得

(16)

令

(17)

同样可以得出

(18)

计算时，各参数与前文相同，假设洞室直径10 m，内衬混凝土的厚度为0.5 m，洞室位于地下100 m深处，洞室内温度为23 ℃(296.15 K)，混凝土的孔隙率η为1%，各参数取值如下：xA=0.5 m，μ=1.8×10-5Pa·s，R=8.314，T=296.15 K，Vm=0.024 5 m3·mol-1，p0=8 MPa，r=5.5 m，r0=5 m，l=6.67 m，η=1%.k取P8级抗渗混凝土，即k=2.380×10-18m2.通过计算，得到图7所示结果.

a 体积

b 压力

Fig.7 Changes of leakage volume and pressure of cylindrical cavern in seepage process

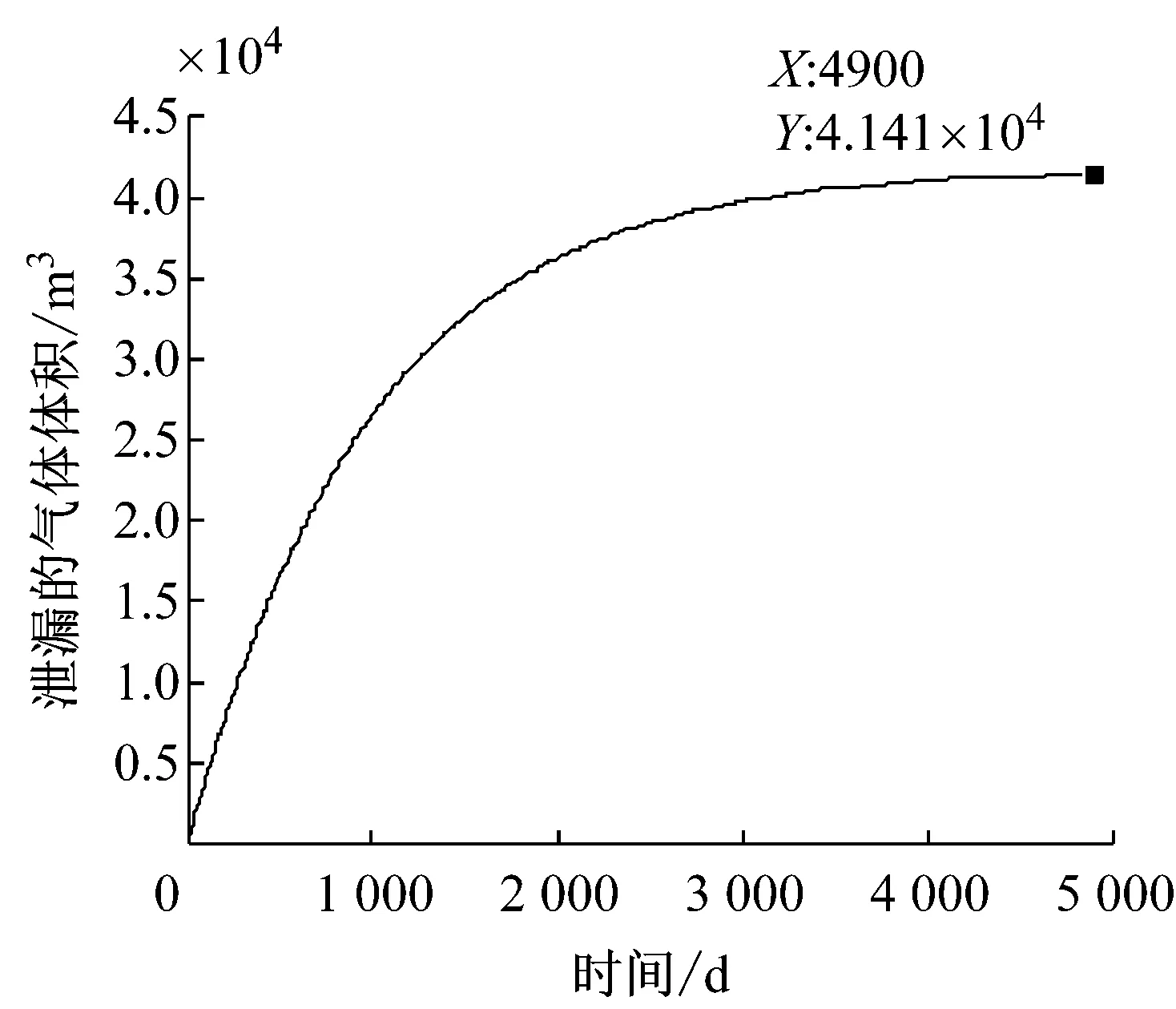
由图7可以看出，在使用圆柱形洞室的时候，在渗透率k=2.380×10-18m2的情况下，洞室内部的气体完全泄漏大概要4 900 d左右，与之前球形洞室的计算结果相比，完全泄漏的时间延长了接近1倍.由图8看出，每天的气体泄漏量也降低到42.11 m3，与球形洞室的69.42 m3相比，也减少了将近40%.同时在这种条件下，当渗透率小于k=2.35×10-17m2时，每天的气体泄漏量就可以低于1%，相比于球形洞室，对于内衬混凝土的渗透率要求也更低.

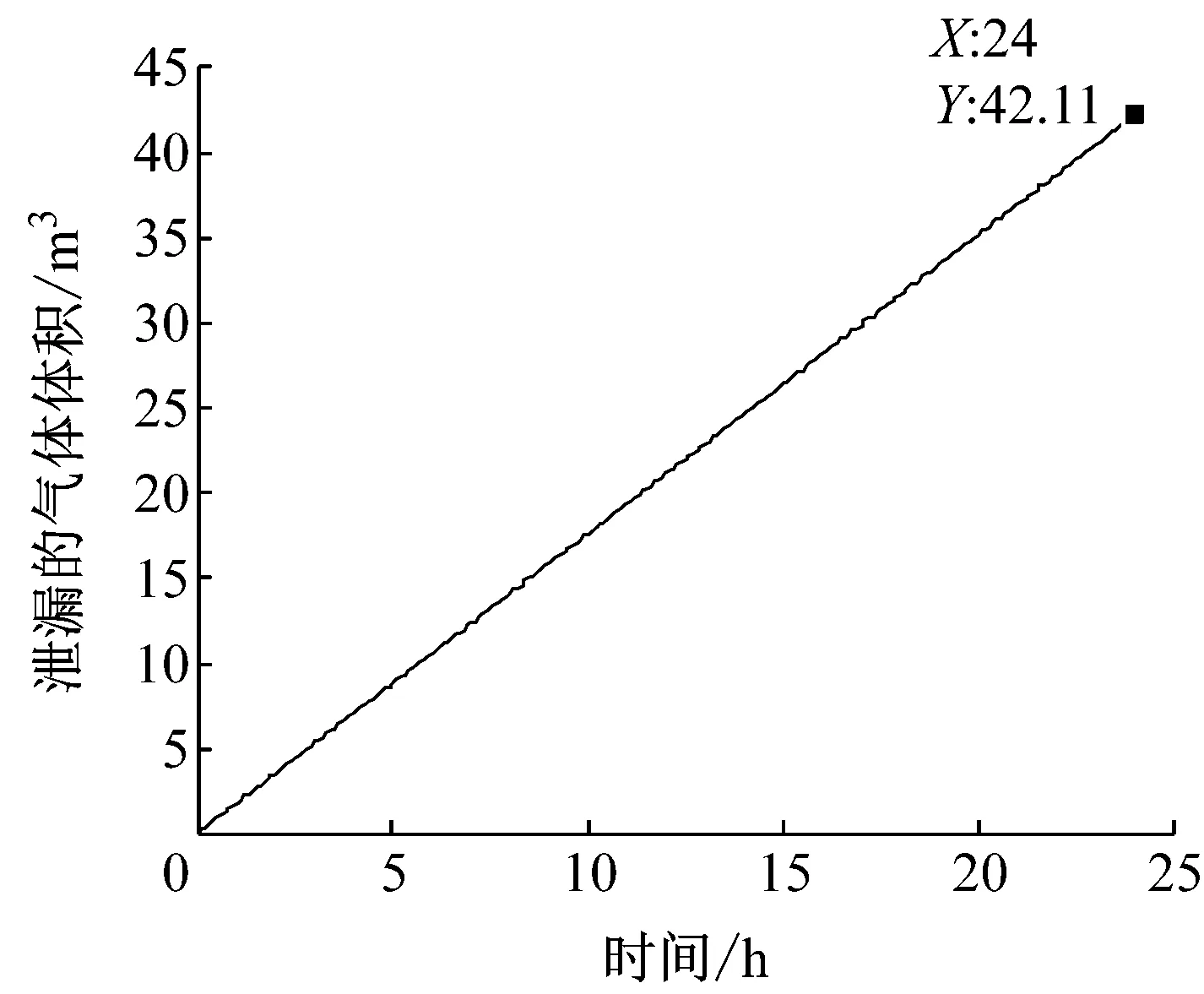
图8 圆柱形洞室每天的气体泄漏量(k=2.380×10-18 m2)

Fig.8 Daily air leakage in cylindrical cavern whenk=2.380×10-18m2

此外，当球形洞室与圆柱形隧道洞室具有相同的直径与体积时，在本文所计算的情况下(洞室直径10 m，衬砌厚度0.5 m)，球形洞室需要约173.3 m3的混凝土，而圆柱形隧道洞室需要约110 m3的混凝土，相比之下，圆柱形隧道洞室所需要的混凝土量也较少，更加具有经济性.

4 结论

针对使用混凝土内衬的硬岩洞室，通过理论分析，得出内衬硬岩洞室中空气泄漏量的理论计算公式，并且分析了可能影响内衬硬岩洞室的各种因素，主要得到以下结论：

(1)对于内衬式压缩空气储能地下储气库，通过考虑内衬混凝土的渗透率及运用达西定律，可以推导出计算空气泄漏的解析公式，在忽略温度的影响时，空气的泄漏量主要和内衬混凝土的渗透率以及洞室形状有关.

(2)计算了一种典型工作条件下地下储气库的气体泄漏情况：球形洞室，直径10 m，内部气体压力8 MPa，温度23 ℃.在此情况下，如果采用P8等级的抗渗混凝土，需要经过3 000 d左右洞室内的气体会全部泄露，同时每天的渗透量是69.42 m3，约占总体积的0.17%，满足压缩空气储能电站的基本运行要求.

(3)在同样的储气库中，当混凝土衬砌的渗透率k=1.43×10-17m2时，每天的渗透量为414 m3，约占总体积的1%，即只要混凝土衬砌的渗透率k<1.43×10-17m2，就可以满足压缩空气储能电站的基本运行要求.

(4)对于球形的地下储气库，每天的气体泄漏量会随着渗透率的增加而线性增加；同时在相同的渗透率条件下，气体泄漏量会随着衬砌厚度的增加而减小.

(5)对于圆柱形隧道式地下储气库，在与球形洞室相同的直径和体积的条件下，气体泄漏量低于球形洞室.当渗透率k<2.35×10-17m2时，洞室每天气体泄漏量将低于1%.

(6)按照所计算的情况，球形洞室需要约173.3 m3的混凝土，而圆柱形隧道洞室需要约110 m3的混凝土.

(7)目前只是分析了理想情况下内衬硬岩洞室的气体泄漏情况，尚未考虑混凝土材料的非均质性以及气体的充放过程衬砌渗透性的影响，这些内容将在未来的研究中进一步分析.

[1] 王蕊. 压缩空气储能技术在电力系统中的应用[J]. 中国电力教育, 2012(S2):447.

WANG Rui. Application of compressed air energy storage technology in power system[J]. China Electric Power Education,2012(S2):447.

[2] 张新敬. 压缩空气储能系统若干问题的研究[D]. 北京:中国科学院研究生院, 2011.

ZHANG Xinjing. Investigation on compressed air energy storage system[D]. Beijing: Institute of Engineering Thermophysics Chinese Academy of Sciences,2011.

[3] 李仲奎, 马芳平, 刘辉. 压气蓄能电站的地下工程问题及应用前景[J]. 岩石力学与工程学报, 2003(S1): 2121.

LI Zhongkui, MA Fangping, LIU Hui. Underground engineering problems in compressed air energy storage and its developing future[J]. Chinese Journal of Rock Mechanics and Engineering,2003(S1): 2121.

[4] Giramonti A J, Lessard R D, Blecher W A,etal. Conceptual design of compressed air energy storage electric power systems[J]. Applied Energy, 1978, 4(4): 231.

[5] Glamheden R, Curtis P. Excavation of a cavern for high-pressure storage of natural gas[J]. Tunnelling & Underground Space Technology, 2006, 21(1):56.

[6] Succar S, Williams R H. Compressed air energy storage: theory, resources, and applications for wind power[R]. Princeton: Princeton Environmental Institute, 2008.

[7] Schulte R H, Critelli Jr N, Holst K,etal. Lessons from Iowa: development of a 270 megawatt compressed air energy storage project in Midwest independent system operator[R]. Albuquerque: Sandia National Laboratories, 2012.

[8] Bauer S J, Gaither K N, Webb S W,etal. Compressed air energy storage in hard rock feasibility study[R]. Albuquerque: Sandia National Laboratories, 2012.

[9] Kim H M, Rutqvist J, Ryu D W,etal. Exploring the concept of compressed air energy storage (CAES) in lined rock caverns at shallow depth: a modeling study of air tightness and energy balance[J]. Applied Energy, 2012, 92(2):653.

[10] Rutqvist J, Kim H M, Ryu D W,etal. Modeling of coupled thermodynamic and geomechanical performance of underground compressed air energy storage in lined rock caverns[J]. International Journal of Rock Mechanics & Mining Sciences, 2012, 52(3):71.

[11] 夏才初, 张平阳, 周舒威,等. 大规模压气储能洞室稳定性和洞周应变分析[J]. 岩土力学, 2014,35(5):1391.

XIA Caichu, ZHANG Pingyang, ZHOU Shuwei,etal. Stability and tangential strain analysis of large-scale compressed air energy storage cavern[J]. Rock and Soil Mechanic, 2014, 35(5):1391.

[12] 周舒威, 夏才初, 张平阳, 等. 地下压气储能圆形内衬洞室内压和温度引起应力计算[J]. 岩土工程学报, 2014, 36(11): 2025.

ZHOU Shuwei, XIA Caichu, ZHANG Pingyang,etal. Analytical approach for stress induced by internal pressure and temperature of underground compressed air energy storage in a circular lined rock cavern[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(11): 2025.

[13] Allen R D, Doherty T J, Fossum A F,etal. Geotechnical issues and guidelines for storage of compressed air in excavated hard rock caverns[R]. Richland: Pacific Northwest Laboratory, 1982.

[14] Zhuang X, Huang R, Liang C,etal. A coupled thermo-hydro-mechanical model of jointed hard rock for compressed air energy storage[J]. Mathematical Problems in Engineering, 2014, 9(2):1.

[15] 陈卫忠, 谭贤君, 伍国军, 等. 含夹层盐岩储气库气体渗透规律研究[J]. 岩石力学与工程学报, 2009, 28(7): 1297.

CHEN Weizhong, TAN Xianjun, WU Guojun,etal. Research on gas seepage law in laminated salt rock gas storage[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(7): 1297.

[16] 钟巍, 田宙, 王铁良, 等. 内含空腔围岩中气体渗流动力学问题的解析计算与试验研究[J]. 岩土工程学报, 2014, 36(2): 339.

ZHONG Wei, TIAN Zhou, WANG Tieliang,etal. Analytic calculation and experimental study on gas seepage dynamics problem of surrounding rock with an internal cavity[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(2): 339.

[17] 龚洛书.混凝土实用手册[M]. 北京:中国建筑工业出版社, 1995.

GONG Luoshu. Concrete practical manual[M]. Beijing: China Architecture and Building Industry Press, 1995.

·下期文章摘要预报·

近断层斜拉桥弹塑性索与阻尼器组合横向减震

管仲国， 游 瀚， 郭 河

研究了近断层地震条件下，使用弹塑性减震索和黏滞阻尼器组合体系进行横向减震的斜拉桥的地震响应和减震规律.采用等效脉冲模型对实际近断层地震进行最小二乘拟合.人工合成Ⅱ类场地下的模拟近断层地震波3组，以永宁黄河大桥为工程背景，对人工近断层地震输入进行非线性时程分析，得到在不同脉冲周期的近断层地震作用下，减震措施设计参数对于塔梁相对位移等响应的影响.结果表明，拟合近断层地震下结构响应与实际地震相差较小，可以满足工程计算需求；近断层地震易造成大位移响应，弹塑性索参数设计时应使结构周期避开脉冲周期；容许减震索进入塑性与保持弹性相比，塔梁相对位移并不会明显增加，甚至在一些情况下会减小.

Analysis of Influence Factors on Air Tightness of Underground Cavern for Compressed Air Energy Storage

YE Bin1, CHENG Zirui1, PENG Yicheng2

(1. College of Civil Engineering, Tongji University, Shanghai 200092, China; 2. Shanghai Electric Power Design Institute, Shanghai 200025, China)

Renewable energy resources are usually intermittent and instable. Compressed air energy storage (CAES) provides a good solution to this problem. Underground air storage cavern is an important part of CAES. Artificially-excavated hard rock cavern attracts wide attention for its little restriction to geology and wide adaptability. The influence of concrete lining permeability on air tightness of underground cavern was investigated. Based on the Darcy’s law, analytical formulas for calculating the amount of air leakage within underground cavern were derived. Using the derived formulas, air leakage condition under a typical CAES operation pressure was analyzed. Furthermore, some influence factors, including lining permeability, lining thickness and cavern shape, were also analyzed. The results show that, when the inner pressure is 8 MPa and impervious concrete of P8 level is used as lining, air leakage rate will be less than 1%, meeting the operational requirements of compressed air energy storage power station. Air leakage will increase linearly with the increase of lining permeability. Compared with spherical cavern, cylindrical cavern has a better leakage-proof effect.

compressed air energy storage; lined rock cavern; air leakage; analytic calculation

2015-09-17

中央高校基本科研业务费专项资金；国家自然科学基金(41472249)

叶 斌(1977—)，男，副教授，工学博士，主要研究方向为地质工程数值分析. E-mail: yebinmail1977@gmail.com

TU91

A