基于平面框架模型的肋式转向结构简化计算方法
2016-11-23邓锦平
徐 栋, 张 宇, 邓锦平
(1.同济大学 土木工程学院,上海 200092;2.天津市政工程设计研究院,天津 300457)
基于平面框架模型的肋式转向结构简化计算方法
徐 栋1, 张 宇1, 邓锦平2
(1.同济大学 土木工程学院,上海 200092;2.天津市政工程设计研究院,天津 300457)
针对肋式转向结构的受力分析和配筋设计,提出了一种基于平面框架模型的简化计算方法,将转向块所在的箱梁节段转化为平面框架模型,其中顶板、腹板、底板转化为三自由度梁单元,转向结构网式划分为等效梁格.由于顶板、腹板的纵向长度对转向结构受力影响很小,因此取为与转向结构同宽,此时平面框架模型如同倒置的简支T梁,平面框架模型中的底板纵向长度可以通过比拟规范中T梁的有效分布宽度确定.与空间网格模型、ANSYS实体模型的相比,简化方法在绝大多数情况下误差仅为5%~20%,且结果偏于安全.最后,将简化方法应用到国内的两座实桥中并与实桥配筋进行对比,发现实桥转向结构配筋量远大于计算值,配筋偏于安全.此简化方法同样适用于配置双层甚至多层转向管道的转向结构的配筋设计.
体外预应力; 转向结构; 平面框架模型; 配筋设计; 简化计算
体外预应力构结构中,体外预应力结构的预应力筋必须通过转向块改变方向形成预应力曲线配筋,这使转向块受到较大的集中力作用,给转向块的受力分析和构造设计带来一定困难.常用转向块的三种形式见图1,即横隔板式、肋式、块式[1].横隔板式和肋式的特点是转向块处可形成抵抗预应力筋张拉力分力的受压支柱,这受压支柱从管道一直形成到桥面,但缺点是增加恒载重量、加大腹板平均厚度、模板构造也较复杂;块式的特点是在底板根部设置很小的混凝土块,给结构施加的附加荷载小,模板也很简单,但是承载能力较横隔板式、肋式小,因为不能形成受压支柱,转向块处的分力必须通过钢筋作用传递到箱内.本文计算分析所采用的转向块结构模型是国内使用较为广泛的混凝土肋式转向块.
对于转向结构的计算分析,现行桥梁规范没有明确规定,目前应用比较广泛的分析方法通常可以归结为三种:第一种是使用大型有限元软件如ANSYS进行空间分析,这种方法能知道转向结构的应力分布情况,但直接利用应力结果配筋比较困难;第二种为空间网格模型方法,通过输出的各个梁格的内力、应力及位移结果,得到结构不同部位的受力状态,从而有针对性的加强配筋[2];第三种为拉压杆模型方法,该方法在桁架模型基础上发展而来,被广泛认为是D区尺寸拟定和配筋设计的有力工具,在国内外都受到了相当的关注,刘钊等针对包括齿块锚固区、横隔梁在内的众多复杂构造或受力区域的拉压杆构形及配筋设计问题进行了研究[3-5],此种方法也被加拿大混凝土设计规范(CSA A23.3-94),美国州际公路和交通运输协会LRFD桥梁规范(1998),美国混凝土协会混凝土结构设计规范(ACI 318-11),欧洲混凝土规范(2004)均采用[6-9],但是目前尚无统一的拉压杆模型的量化评价准则.
1 转向结构简化计算的平面框架模型
计算分析采用的箱梁截面图和节段模型渲染图分别见图1和图2,箱梁高4 m,顶宽16.4 m,底宽8.5 m,顶底板厚0.25 m,腹板厚0.4 m,肋式转向块厚0.5 m,转向块底部有四根体外束穿过,假定每根体外束转向力均为100 kN.

图1 转向块处箱梁截面(cm)

图2 节段模型渲染图
在肋式转向结构的受力分析中发现,转向管道以上部分受压,约70%左右的转向力均以压力方式由转向结构传递至整个箱梁框架,转向管道以下部分则受拉,约20%左右的转向力以拉力的方式通过转向结构传至箱梁框架[10].建立转向结构简化计算的平面框架模型,如图3所示,在平面框架模型中,支承可以加在顶板和腹板相交的节点上,此时,对于转向结构本身的受力特性,这种支承方式是合理的.

图3 平面框架模型
在平面框架模型中,顶板、腹板、底板简化为三自由度梁单元,它们的截面尺寸(即各板块的纵向有效长度)将在稍后进行讨论;转向结构则视为一块板,网式划分后等效为一片正交梁格,见图4.

a 等效纵横梁
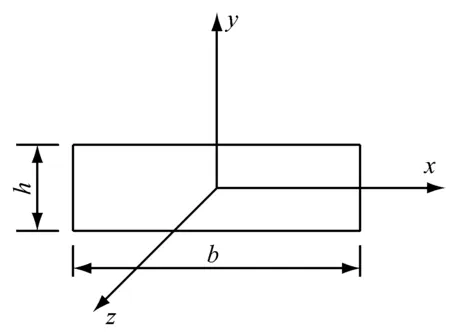
b 划分截面
根据梁格理论,等效纵横梁的“划分截面”与传统单元截面特性计算一致,由离散后的实际截面尺寸计算,详情见参考文献[11].
为得到各板块的纵向有效长度,在平面框架模型中,分别将顶板、腹板以及底板的纵向长度由0.5 m变大到4 m,单独分析它们对转向结构中传力机制的影响.转向力数值上等于转向管道上梁格压力与下梁格拉力之和,其中下梁格的拉力值是转向结构的配筋设计的重要指标.如图5所示,顶板、腹板的纵向长度对转向管道下梁格的拉力值影响很小,也就是说,模型中顶板、腹板的纵向长度对转向力的传力机制影响不大,可以将顶板和腹板的纵向长度取为与转向结构同宽,只需要确定底板的有效纵向长度.此时箱梁节段如同一个倒置的简支T梁,竖直向上的转向力相当于T梁翼缘受压,如图6所示.
于是,在平面框架模型中底板的纵向长度就可以按T梁的有效分布宽度来取用.《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62-2004)规定,T形截面内梁的翼缘有效宽度,应按下列规定取其中的最小值[12]:

图5 顶底板、腹板长度对拉力值的影响
(1)对于简支梁,取计算跨径的1/3.对于连续梁,各中间跨正弯矩区段,取该计算跨径的0.2倍;边跨正弯矩区段,取该计算跨径的0.27倍;各中间支点负弯矩区段,取该支点相邻两计算跨径之和的0.07倍;
(2)相邻两梁的平均间距;

图6 转向结构处T梁的简化图式

考虑到众多的箱形截面宽高比小于2,这样,图7中的T梁就相当于深梁,按最小值取用可能会有所偏差.这里根据规范中第1条和第3条规定分别计算箱梁框架中底板沿纵向的有效长度:箱梁底板宽度的1/3;转向结构厚度与12倍底板厚度之和.

图7 空间网格模型简化原理示意
2 简化方法的准确性检验
2.1 空间网格模型与ANSYS实体的对比分析
空间网格模型是一种桥梁精细化分析方法,采用梁格法原理将薄壁箱形截面视为由顶底板等若干块板组成(转向结构也当作一块竖向的板),对每一块板进行梁格划分,用划分后的梁格来等效代替各个板的受力,图7是空间网格模型简化原理示意[2].
取箱梁纵向长度为8 m,分别建立空间网格模型和ANSYS实体模型:空间网格模型以及转向结构梁格划分方式见图8和图9;ANSYS实体模型为尽量减小转向管道周围局部应力的影响,转向管道用边长为0.06 m的正方形,转向力以面压力的形式作用在转向管道上表面.
考察两种模型中转向管道上、下方的混凝土竖向应力,空间网格模型中为1~4#梁格的轴向正应力值,ANSYS实体模型中为距离转向管道上、下缘5 cm处以及转向管道中心处的截面正应力分布,对比结果如图10所示.

图8 空间网格模型

图9 转向结构处梁格划分示意图
在转向力作用下,空间网格模型中各梁格的受力情况和实体分析结果如下:空间网格模型中转向力作用节点以上梁格全部承受压力,最大压应力为-0.517 MPa,出现在3#梁格中,拉应力主要分布在转向力作用节点以下,最大拉应力出现在靠近腹板的1#梁格中,为0.141 MPa;ANSYS中最大压应力和和最大拉应力均出现在同样位置,但应力结果比空间网格模型的应力值大,分别为-1.23 MPa和0.302 MPa.这是容易理解的,空间网格模型中梁格的应力结果为单个梁格上的平均应力,必定会小于实体分析中的最大值.选取靠近腹板的转向管道以下的拉应力区域,利用ANSYS相关的面操作命令,可以得到其在箱梁竖向的轴力为19.2 kN,对应的空间网格模型的1#梁格轴力计算结果比实体模型计算结果大1.9 kN,偏差约为9%.由于用于配筋设计的是一个受力相同区域的应力之和(力),故空间网格模型的计算结果是比较准确的.
为方便数据分析,下面将采用空间网格模型方法检验平面框架模型简化方法的准确性.
2.2 空间网格模型与平面框架模型的对比分析
在转向块受力性能的参数分析中发现,只有底板厚度、箱梁高度以及斜腹板斜率变化这三组参数的影响较大[13],故选取此三组参数作为变量,将简化方法得到的转向管道下梁格拉力的最大值与相应的空间网格模型计算结果进行比较,用以验证简化方法的准确性,详细结果见表1所示.

b ANSYS转向管道以上截面

c ANSYS转向管道以下截面

d ANSYS转向管道中心截面
由计算结果可见:根据规范规定第1条确定箱梁底板纵向有效长度时,平面框架模型计算结果在绝大多数情况下较空间网格模型计算结果大5%~19%,在底板厚度较厚的情况下,平面框架结果略小于空间网格计算结果,但差距不大,仅3%,在斜腹板斜率为1/4时,两者计算结果差距最大,有19%,但平面框架模型计算结果偏于安全;根据规范规定第3条确定箱梁底板纵向有效长度时,平面框架模型计算结果在绝大多数情况下较空间网格模型计算结果大14%~20%,当箱梁斜腹板斜率为1/4时,平面框架模型计算结果较空间网格模型大42%,误差较大.考虑到转向结构在体外预应力结构的重要作用,建议在选取箱梁框架长度的时候,根据规范规定第3条取用,即转向结构厚度与12倍的底板厚度之和.

表1 转向管道下最大拉力值比较表(kN)
注:*原模型中直腹板绕腹板与底板的交点旋转建立不同斜率的斜腹板模型,进行参数分析
3 简化计算方法在实桥中的应用
3.1 重庆新滩綦江大桥
重庆市新滩綦江大桥(75+130+75 m连续刚构桥)是国内首次将体外预应力技术应用到大跨连续刚构并实施的桥梁工程.主桥按双向六车道设计,分左右两幅桥,各宽16.75 m.左幅连续刚构为全体内预应力体系;右幅连续刚构为体内、体外混合的预应力体系,其中一期束为体内预应力体系,二期束为体外预应力体系.
该桥某转向结构厚1 m,体外预应力钢束采用27-∅815.24喷环氧无粘接钢绞线,整个转向结构横截面处共有四根体外预应力钢束通过,转向角度为11.5°.体外预应力钢束的锚下控制张拉应力为σ=1 209 MPa,单根锚下控制张拉力168.1 kN,因此单个转向管道上作用的钢束转向力为905 kN.转向结构如图11所示.

图11 新滩綦江大桥的转向结构(单位:cm)
分别建立空间网格模型和简化方法的平面框架计算模型,平面框架中箱梁长度仍分别按规范第1条和第3条选用.根据04桥规裂缝计算公式,当钢筋直径为20 mm,裂缝宽度为0.2 mm时,可以求得受拉构件中钢筋的应力为174 MPa,因此,钢筋应力可以偏安全的取为150 MPa.如果按转向结构中钢筋的应力为150 MPa,就可以得到两种计算结果的配筋量,计算得出该桥转向结构转向管道以下的拉力值以及配筋数量如表2所示.
当箱梁长度为1/3底板宽度时,框架分析法的拉力值计算结果较空间网格模型计算结果小了7.4 kN,约4.8%,相应的钢筋面积也比后者少49.而箱梁长度为转向结构厚度与12倍底板厚度之和时,拉力值较空间网格模型大了17.9 kN,所需配筋面积增加了120 mm2,由此增加的钢筋数量是非常有限的.

表2 新滩綦江大桥桥转向结构计算结果
3.2 苏通长江大桥深水区段引桥
苏通长江公路大桥深水区段中的75 m跨连续梁采用节段预制拼装施工,为体内、体外预应力混合配束结构,其转向结构如图12所示.


图12 苏通大桥75 m引桥转向结构(单位:m)
分别建立空间网格模型和简化方法的平面框架计算模型,平面框架中箱梁长度仍分别按规范第1条和第3条选用.如果按转向结构中钢筋的应力为150 MPa,就可以得到两种计算结果的配筋量,计算得出该桥转向结构转向管道以下的拉力值以及配筋数量如表3所示.

表3 苏通桥75 m引桥转向结构计算结果
由表中计算结果可见,当箱梁长度为1/3底板宽度时,框架分析法和空间网格模型的计算结果是一致的.而箱梁长度为转向结构厚度与12倍底板厚度之和时,拉力值较空间网格模型大了21 kN,所需配筋面积增加了140 mm2.
3.3 理论计算与实桥配筋量的对比
转向结构中通常包括三种类型的普通钢筋:环筋、闭口箍筋以及靠近混凝土表面布置的纵横向钢筋.其中,纵横向钢筋为构造钢筋,按一定的配筋率在转向结构混凝土表面均匀布置.转向管道区设有两种受力钢筋,一种是围住单个转向管道的环筋,另一种是围住所有转向管道的闭口箍筋,环筋是需要设计计算的受力钢筋,闭口箍筋一般属于构造钢筋.图13为苏通大桥引桥转向结构的配筋.
假设拉力全部由环筋承担,可以很方便的计算围住单个转向管道的环筋钢筋面积.根据实桥中各转向块的环筋布置情况,统计得到简化计算结果和实桥环筋面积的比较见表4所示,表中比较的数据是单个转向管道单侧环筋的面积.
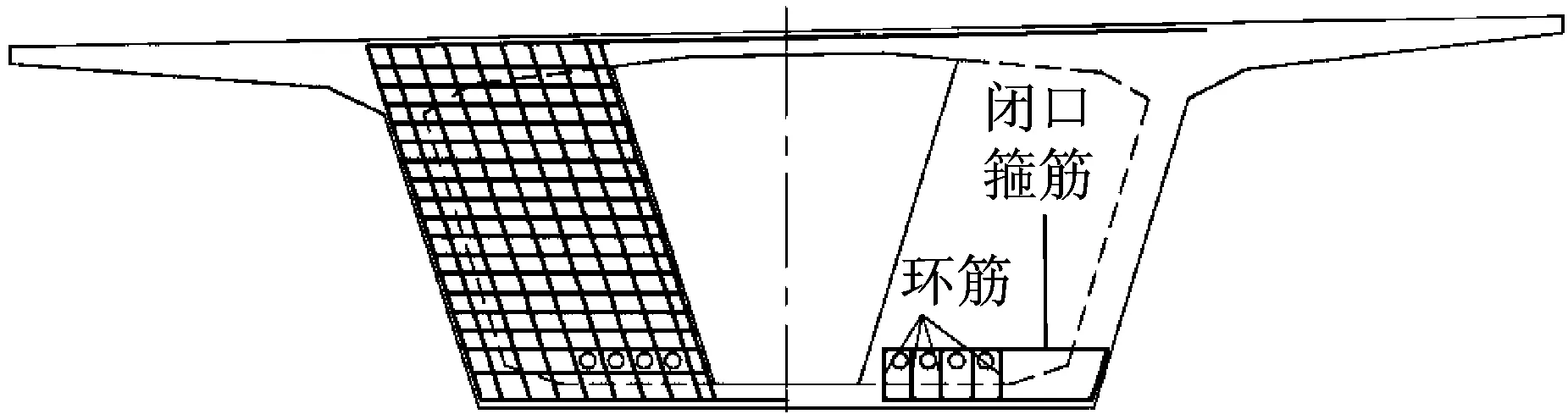
图13 苏通大桥引桥段转向结构配筋图

表4 理论计算配筋量和实桥的比较
由表中数据可见,这三座桥梁中转向结构的配筋均偏于安全,远大于理论值.
4 平面框架模型在布置双层转向管道的转向结构的适用性
当在一个截面上需要转向的钢束比较多时,可以将钢束在竖向作双层布置,图14为错开布置和平行布置两种双层布置方式.

图14 转向管道的双层布置(单位:cm)
本文通过对转向管道平行布置的计算来考察平面框架模型在这种类型转向结构分析中的适用性.建立平面框架模型,箱梁底板纵向长度取为转向结构厚度与底板厚度的12倍之和,作用转向力均为100 kN,转向管道区梁格划分见图15.将计算得到的转向管道区竖向梁格的最大轴力与空间网格模型进行比较,如表5所示.
由表5可见,框架分析法的计算结果比空间网格模型稍大.因此,可以认为,框架分析法对这种转向结构受力性能的计算分析同样适用于配置双层甚至多层转向管道的转向结构的受力分析和配筋设计.

图15 转向结构处梁格划分示意图

参数空间网格模型平面框架模型压(上层管道上)拉(下层管道下)压(上层管道上)拉(下层管道下)力值/kN36.587.340.687.8应力/MPa0.3650.8730.4060.878
5 结论
(1)针对转向块结构的受力分析和配筋设计,简化计算方法比较简单,同时又具备不错的精度.与空间网格模型相比,简化方法的结果在绝大多数情况下较为吻合,并且偏于安全.根据规范中T形截面内梁的翼缘有效宽度规定的第1条确定箱梁底板长度的框架模型计算结果在绝大多数情况下较空间网格模型计算结果大5%~19%;根据规定的第3条确定箱梁长度的平面梁格模型计算结果在绝大多数情况下较空间网格模型计算结果大14%~20%.
(2)考虑到转向结构在体外预应力结构的重要作用,建议在选取箱梁底板纵向长度的时候,根据规范规定第3条取用,即转向结构厚度与12倍的底板厚度之和.
(3)实桥对比分析表明,理论配筋远低于实桥配筋,实际桥梁中转向结构的配筋均偏于安全.
(4)简化方法同样适用于配置双层甚至多层转向管道的转向结构的受力分析和配筋设计.
[1] Rogowsky D M, Marti P. Detailing for post-tensioning[M]. Bern: VSL International, 1992.
[2] 徐栋, 赵瑜, 刘超. 混凝土桥梁结构实用精细化分析与配筋设计[M]. 北京:人民交通出版社, 2013.
XU Dong, ZHAO Yu, LIU Chao. Practical precise modeling and reinforcement design for concrete bridge structures[M]. Beijing: China Communications Press, 2013.
[3] 陈晓宝, 滕育梅. 结构混凝土拉压杆模型法配筋设计[J]. 合肥工业大学学报: 自然科学版, 2001, 24(2): 160.
CHEN Xiaobao, TENG Yumei. Design for reinforcement of structural concrete with Strut-and-Tie model method[J]. Journal of Hefei University of Technology: Natural Science, 2001, 24(2): 160.
[4] 郑和晖, 刘钊, 贺志启. 混凝土箱梁桥的横隔梁拉压杆模型及配筋设计[J]. 工程力学, 2011, 28(5): 97.
ZHENG Hehui, LIU Zhao, HE Zhiqi. Strut-and-tie models for diaphragms of concrete box-girder bridges and reinforcement design [J]. Engineering Mechanics, 2011, 28(5): 97.
[5] 林波, 刘钊, 吕志涛. 体外预应力独立矩形齿块锚固区的拉压杆模型及配筋设计[J]. 工程力学, 2011, 28(12): 59.
LIN Bo, LIU Zhao, LÜ Zhitao. Strut-and-tie model and reinforcement design method for isolated rectangular anchor block for external tendons [J]. Engineering Mechanics, 2011, 28(12): 59.
[6] Standard C S A. Design of concrete structures[S]. Rexdale: Canadian Standards Association, 1994.
[7] AASHTO. AASHTO LRFD bridge construction specifications[S].Washington D C: American Association of State Highway and Transportation Officials,1998.
[8] ACI. ACI 318-11 ACI building code requirements for reinforced concrete and commentary[S].Farmington Hills: American Concrete Institute, 2011.
[9] British Standards Institution. Eurocode 2: design of concrete structures: part 1-1: general rules and rules for buildings[S]. Brussels: British Standards Institution, 2004.
[10] 徐栋. 桥梁体外预应力设计技术[M]. 北京:人民交通出版社, 2008.
XU Dong. External prestressing design in bridge[M]. Beijing: China Communications Press, 2013.
[11] Hambly E C. Bridge deck behaviour[M]. London: E & FN Spon, 1976.
[12] 中交公路规划设计院有限公司. JTG D62—2004 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. 北京:人民交通出版社, 2004.
CCCC Highway Consultants Co Ltd. JTG D62—2004 Code for design of highway reinforcement concrete and prestressed concrete bridges and culverts[S]. Beijing: China Communications Press, 2004.
[13] 邓锦平.体外预应力混凝土桥梁关键部位设计方法[D]. 上海:同济大学土木工程学院,2008.
DENG Jinping. Design of important parts of externally prestressed concrete bridges[D]. Shanghai: College of Civil Engineering of Tongji University,2008.
Simplified Calculation Method of Rib Deviator Based on Planar Frames
XU Dong1, ZHANG Yu1, DENG Jinping2
(1. College of Civil Engineering, Tongji University, Shanghai 200092, China;2.Tianjin Municipal Engineering Design & Research Institute, Tianjin 300457, China)
A simplified calculation method based on planar frames is proposed for mechanical analysis and reinforcement design of rib deviator. In the planar frame model, top deck, bottom deck and webs of box girder are represented by 3 dof beams, while the rib deviator is equivalent to vertical and horizontal girders. Longitudinal lengths of the top deck and webs can be set the same as the thickness of the rib deviator for its tiny effect on the analysis. Then the planar frame model can be treated as an upside-down T-shape beam, so the longitudinal length of the bottom deck can be obtained by analogy of the effective distribution width of T-shape beam. Compared with spatial grid model and ANSYS solid model, the planar frame model has a good coherence with only 5%~20% error in most cases and the solutions are conservative. In the next part, the application results of the simplified calculation method to two practical bridge structures show that the realistic reinforcement amount of the rib deviator is much larger than that by theoretical solution. The simplified calculation method can also be applied to two-layer or multilayer ducts deviators.
external prestressing; deviator; planar frame; reinforcement design; simplified calculation method
2015-12-10
徐 栋(1966—),男,教授,博士生导师,工学博士,主要研究方向为混凝土桥梁结构.E-mail: xu_dong@ tongji.edu.cn.
U448.35
A
