Maxwell阻尼耗能结构非平稳地震响应解析分析

李创第， 李 暾， 尉宵腾， 葛新广， 邹万杰

(1.广西科技大学 土木建筑工程学院，广西 柳州 545006； 2. 广西大学 土木建筑工程学院，南宁 530004)



Maxwell阻尼耗能结构非平稳地震响应解析分析

李创第1， 李 暾1， 尉宵腾2， 葛新广1， 邹万杰1

(1.广西科技大学 土木建筑工程学院，广西 柳州 545006； 2. 广西大学 土木建筑工程学院，南宁 530004)

对单自由度广义Maxwell和多自由度Maxwell阻尼耗能结构非平稳随机地震响应问题进行了系统研究。首先通过构建单自由度和多自由度耗能结构在原始空间和扩阶空间上的特征值和特征向量的精确对应关系，将耗能结构位移、速度和阻尼器受力的时域响应计算公式用结构原始空间上的特征值和特征向量解析表出；然后针对7种经典均匀调制白噪声地震激励和2种经典均匀调制滤过白噪声地震激励，获得了耗能结构位移、速度和阻尼器受力的非平稳均方响应的解析解，并使耗能结构非平稳响应的解析分析与计算，完全转化为耗能结构在原始空间的特征值和特征向量的解析分析与计算，从而构建了基于耗能结构非扩阶特征值和特征向量分析，获得耗能结构非平稳地震响应解析解的一整套方法。

Maxwell阻尼器；耗能结构；阻尼器受力响应；非平稳随机过程；解析解

黏滞和黏弹性阻尼器等被动控制技术已被广泛应用[1-4]。由于实际地震动具有非平稳随机特性，各种均匀调制白噪声和滤过白噪声非平稳地震动模型已用于结构分析[5-11]，故分析阻尼器耗能结构非平稳随机地震响应特性具有理论和工程意义。Maxwell模型阻尼器本构方程简单，易于扩阶，模型计算参数便于从试验数据拟合[12-13]，且一般流体阻尼器比较符合Maxwell模型，黏弹性阻尼器也可用Maxwell模型近似表示或用广义Maxwell模型表示，故Maxwell模型阻尼器耗能结构动力响应特性分析受到日益重视[14-17]。文献[14]用扩阶复模态法分析了Maxwell阻尼器耗能结构位移响应特性；文献[15-16]用扩阶复模态法分析了Maxwell黏滞阻尼器耗能结构在Knain-Tajimi谱随机地震作用下的位移平稳方差响应，由于尚未获得平稳响应解析解，故研究侧重于大量数值计算结构的归纳与总结；而且上述研究均尚未涉及对耗能结构安全有重大影响的阻尼器受力的响应分析；此外，采用常规扩阶复模态法，导致耗能结构在原始空间和扩阶空间的对应关系不明确，扩阶变量多，计算效率低，工程人员较难理解。

本文通过构建耗能结构在原始空间和扩阶空间上特征值和特征向量的精确对应关系，获得耗能结构非平稳位移、速度、特别是阻尼器受力响应的解析解，建立耗能结构基于非扩阶特征值和特征向量分析的非平稳地震响应解析解的一整套分析方法。

1 单自由度耗能结构响应解析式

1.1 结构运动方程

(1)

(2)

式中：阻尼器松弛参量μj=kj/cj，(j=1,2,…,n)。

图1 单自由度耗能结构计算简图Fig.1 Calculation diagram of the SDOFenergy dissipation structure

将式(2)代入式(1)，运动方程可简化为：

(3)

式中:频率、阻尼比和阻尼参量ω0、ξ0和βj分别为：

1.2 原始结构特征值和特征向量分析

在零初始条件下，对方程(3)取拉氏变换，得：

(5)

(6)

由文献[18]，结构特征值sj及其对应的特征向量uj的方程为：

(7)

D(sj)uj=0

(8)

由上述两式，可求得原始结构(n+2)个特征值sj及其对应的非零特征向量uj，(j=1～n+2)。

1.3 扩阶结构特征值和特征向量分析

(1)扩阶结构方程

令：

(9)

(10)

则原始结构方程(3)可扩阶为：

(11)

式中：

(12)

(13)

(14)

由线性系统稳定性理论[19]，扩阶方程组(11)的稳定条件是其所有特征值的实部均为负数，故引入扩阶变量v(t)和yj(t) (j=1,2,…,n)后，原结构系统(3)的参数ω0、ξ0、μl、βl(l=1,2,…,n)的取值范围是：使扩阶方程组(11)的所有特征值的实部均为负数的一切值。至于具体分析，可按常用的Routh-Hurwitz判据分析即可[19]。

(2)扩阶结构特征值分析

方程(11)的特征值方程为：

其中：I为 (n+2)阶单位矩阵。当n=1时，将行列式按最后一列展开，得：

(16)

当n=2时，将行列式按最后一列展开，并利用式(16)，得：

(17)

以此类推，当n=n时，特征值方程(15)化为：

(18)

故原始结构和扩阶结构的特征值方程(7)和(18)完全相同，所求的的特征值sj(j=1～n+2)也完全相同。

(3)扩阶结构特征向量分析

方程(11)与特征值sj对应的右、左模态φj和ψj方程为：

[Isj+A]φj=0

(19)

[Isj+A]Tψj=0

(20)

其中：j=1～n+2。

令：

(21)

将式(21)代入式(19)，并经化简，可得：

D(sj)φ1j=0

(22)

φ2j=sjφ1j

(23)

(24)

对比式(8)和(22)知，φ1j=uj；故右复模态φj为：

(25)

同理，由式(20)，可得：

ψj=

(26)

式(18)、(25)、(26)表明：扩阶结构的特征值与原始结构的特征值完全相同，且扩阶结构的特征向量可用原始结构的特征向量表出。

1.4 扩阶结构响应的降阶解析式

由复模态理论[20]，在零初始条件下，扩阶方程(11)的解为：

(27)

(28)

式中：

(29)

(30)

γj=2sj+2ξ0ω0+

(31)

故结构位移响应为：

(32)

式中：

(33)

同理，结构速度和阻尼器受力响应分别为：

(34)

(35)

式中：

(36)

式(32)、(34)、(35)表明：结构的各种响应s(t)的计算归结于原始结构的特征值sj的计算，s(t)有统一形式的表达式：

(37)

2 多自由度耗能结构响应解析式

2.1 结构运动方程

图2 多自由度耗能结构计算简图Fig.2 Calculation diagram of the Multi-DOFenergy dissipation structure

(38)

(i=1,2,…,n)

(39)

式中:阻尼器松弛参量αi、阻尼器向量p、位置转换向量J和矩阵Tp分别为：

αi=k0i/c0i，(i=1,2,…,n)

(40)

(41)

(42)

(43)

将式(39)代入式(38)，结构运动方程可化为：

式中，阻尼器系统的松弛矩阵h(t)为：

(46)

2.2 原始结构特征值和特征向量分析

在零初始条件下，对方程(45)取拉氏变换，得：

(47)

(48)

由文献[18]，结构特征值sj及其对应的特征向量uj的方程为：

(49)

D(sj)uj=0

(50)

由上述两式，可求得原始结构3n个特征值sj及其对应的非零特征向量uj，(j=1～3n)。

2.3 扩阶结构特征值和特征向量分析

(1)扩阶结构方程

令：

(51)

可将结构方程(38)、(39)扩阶为：

(52)

式中：

(53)

(54)

(55)

显然，引入扩阶变量v(t)后，系统相关参数的取值范围是使扩阶方程组(52)的所有特征值的实部均为负数的一切值[19]，至于具体分析，可按常用的Routh-Hurwitz判据分析即可[19]。

(2)结构特征值和特征向量分析

扩阶方程(52)的特征值λj对应的右、左特征向量Φj和Ψj方程分别为：

[Bλj+A)]Φj=0

(56)

[Bλj+A]TΨj=0

(57)

令：

(58)

将式(58)代入式(56)，并经化简，可得：

D(λj)φ1j=0

(59)

φ2j=λjφ1j

(60)

(61)

对比式(50)和(59)知，扩阶结构的3n个特征值λj=sj，右特征向量Φj的分量φ1j=uj，故扩阶右特征向量Φj与原特征向量uj的对应关系为：

(62)

同理，由式(57)，可得Ψj与uj的对应关系为：

(63)

式(59)、(62)、(63)也表明：扩阶结构的特征值与原结构的特征值完全相同，且扩阶结构的特征向量可用原始结构的特征向量表出。

2.4 扩阶结构响应的降阶解析式

由复模态理论[20]，在零初始条件下，扩阶方程(52)的解为：

(64)

(65)

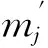
(66)

(67)

故结构各种响应降阶解析式为：

(68)

(69)

(70)

式(69)～(70)表明：结构的各种响应计算归结于原结构特征值sj和特征向量uj的计算。

(71)

(72)

(73)

由式(68)～(70)，结构位移、速度、阻尼器等组合响应S(t)均可统一表示为：

(74)

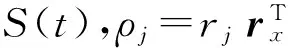
3 耗能结构非平稳响应解析式

3.1 非平稳地震激励模型

(75)

(76)

(77)

式中：E[·]表示取数学期望值；S0为地震谱强度；δ(·)为dirac函数。

由于函数δ(τ)的性质，取I(t)=2πA2(t)为调制强度函数，则式(77)可进一步表示为：

(78)

(79)

(80)

(81)

q=-α+jβ

(82)

(83)

(84)

相关参数S0、ωg、ξg的具体取值可参见文献[5]。

3.2 结构非平稳响应表达式

由式(37)和(74)知，对应于单和多自由度Maxwell阻尼减震结构，它们的位移、速度、层间位移、层间速度、阻尼器受力等一般结构响应量S(t)均可统一表示为：

(85)

式中：N为减震结构特征值的总数；ρj为结构响应S(t)对应的已知组合系数；bj(t)为标准一阶系统对地震激励的响应，即：

(86)

(87)

由式(85)和(87)，结构一般响应S(t)的非平稳协方差函数的表达式为：

E[S(t)S(t+τ)]=

(88)

(89)

3.3 均匀调制白噪声地震激励下的响应特性

将式(78)代入式(89)，可得此种情况响应特性的表达式为：

(90)

下面给出几种经典调制情况下上式的具体解析解。

3.3.1 阶跃型调制强度函数

由于：

(91)

故式(90)化为：

(92)

3.3.2 余弦型调制强度函数[10]

由于：

I(t)=U(t)(c+dcosωt)

(93)

式中：c,d,ω为已知常数；c≥d。

故式(90)化为：

(94)

3.3.3 正弦型调制强度函数[10]

由于：

I(t)=U(t)(c+dsinωt)

(95)

式中：c,d,ω为已知常数；c≥d。

故式(90)化为：

(96)

3.3.4 分段连续型调制强度函数[6]

由于：

(97)

式中：I0,c,t1,t2均为常数。

故式(90)化为：

0≤t≤t1

(98)

t1≤t≤t2

(99)

t≥t2

(100)

3.3.5 Shinozuka-Sato型调幅函数[7]

由于：

A(t)=U(t)(e-a1t-e-a2t)

(101)

I(t)=2πU2(t)(e-a1t-e-a2t)2

(102)

式中：a1、a2为常数。

故式(90)化为：

(103)

3.3.6 Iyengar型调幅函数

由于：

A(t)=U(t)(b+ct)e-at

(104)

I(t)=2πU2(t)(b+ct)2e-2at

(105)

式中：a,b,c为常数。

故式(90)化为：

(106)

3.3.7 Goto-Toki型调幅函数[9]

由于：

(107)

(108)

式中：A0,tp为常数。

故式(90)化为：

(109)

3.4 均匀调制滤过白噪声地震激励下的响应特性

将式(79)代入式(89)，可得此种情况响应特性的表达式为：

(110)

下面给出2种经典调制情况下上式的具体解析解。

3.4.1 阶跃型调制强度函数

由于：

A(t)=U(t)

(111)

故式(110)化为：

(112)

3.4.2 Shinozuka-Sato型调幅函数[7]

由式(101)，故式(110)化为：

(113)

4 算 例

图3 单自由度耗能结构计算简图Fig.3 Calculation diagram of the SDOF energy dissipation structure

计算结果为：结构位移非平稳响应方差如图4～图6所示；结构速度非平稳响应方差如图7～图9所示；阻尼器受力的非平稳响应方差如图10和图11所示。

从以上计算结果可以看出：

(1)系统在阶跃型白噪声(也即突加平稳白噪声)激励下，在瞬态过程消失后，系统的随机均方响应趋于平稳值。

(2)系统在分段连续型白噪声激励下，系统的随机均方响应随强度调制函数而变化，均方响应曲线的平坦部分对应于系统在平稳白噪声激励下的稳态均方值。

(3)在Shinozuka-Sato型调幅滤过白噪声激励下，系统的随机均方响应与调幅函数曲线相似，呈单峰形状。

(4)在阻尼器两分支Maxwell单元的松弛性能参数不变的情况下，同步增加两分支Maxwell单元的刚度和阻尼系数，也即工况Ⅰ～工况Ⅳ，系统的位移和速度均方响应减少，而系统的阻尼器受力均方响应增大，说明增加同类型的阻尼器，可进一步减少结构响应。

图4 阶跃型白噪声激励下位移响应方差

Fig.4 Response variance of displacement under Step-white noise excitation

图5 分段连续型白噪声激励下位移响应方差

Fig.5 Response variance of displacement under Piecewise continuous white noise excitation

图6 Shinozuka-Sato型调幅滤过白噪声激励下位移响应方差

Fig.6 Response variance of displacement under amplitude modulation filtered white noise excitation with Shinozuka-Sato type

图7 阶跃型白噪声激励下速度响应方差

Fig.7 Response variance of velocity under Step-white noise excitation

图8 分段连续型白噪声激励下速度响应方差

Fig.8 Response variance of velocity under Piecewise continuous white noise excitation

图9 Shinozuka-Sato型调幅滤过白噪声激励下速度响应方差

Fig.9 Response variance of velocity under amplitude modulation filtered white noise excitation with Shinozuka-Sato type

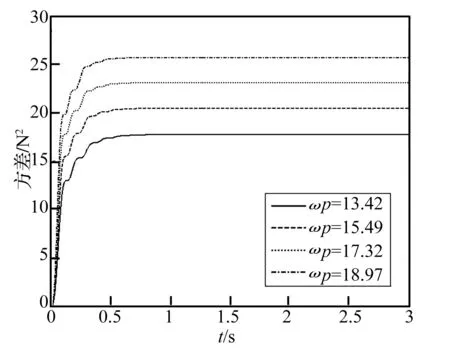
图10 阶跃型白噪声激励下阻尼器响应方差Fig.10 Response variance of damper under Step-white noise excitation

图11 分段连续型白噪声激励下阻尼器响应方差Fig.11 Response variance of damper under Piecewise continuous white noise excitation

5 结 论

对单自由度广义Maxwell和多自由度Maxwell阻尼减震结构的非平稳随机地震响应解析分析问题的系统研究，可得出如下结果：

(1)单自由度和多自由度Maxwell阻尼耗能结构在原始空间和扩阶空间上的特征值完全相同，且扩阶空间上的特征向量可用原始空间上的特征向量完全表出。

(2)耗能结构位移、速度和阻尼器受力的响应计算公式可通过原始空间上的特征值和特征向量解析表出。

(3)耗能结构在7中经典均匀调制白噪声和2种经典均匀调制滤过白噪声地震激励下的位移、速度和阻尼器受力的均方响应解析解也可通过结构原始空间上的特征值和特征向量解析表示。

利用上述结果，可使Maxwell耗能结构的非平稳地震响应分析与计算转化为耗能结构在原始空间的特征值与特征向量的分析与计算，从而使分析与计算得到简化，结构振动特性，特别是阻尼器的受力特性得到更好地理解和把握。

[1] SOONG T T, DARGRUSH G F. Passive engrgy dissipation systems in structural engineering [M]. England: John Wiley and Ltd,1997.

[2] CHRISTOPOULOS C, FILIATRULT A. Principle of passive supplemental damping and seismic isolation [M]. IUSS Press, Pavia, Italy, 2006.

[3] 周云. 黏弹性阻尼减震结构设计[M]. 武汉：武汉理工大学出版社，2006.

[4] 李创第，邹万杰，葛新广，等. 多自由度一般积分型黏弹性阻尼器减震结构的随机响应与等效阻尼[J]. 工程力学，2013，30(4)：136-145.

LI Chuangdi, ZOU Wanjie, GE Xinguang, et al.Random response and equivalent damping of MDOF dissipation structures with general integral model viscoelastic dampers [J]. Engineering Mechanics, 2013, 30(4): 136-145.

[5] 胡聿贤. 地震工程学[M]. 第2版.北京：地震出版社，2006.

[6] AMIM A, ANG A H S. Non-stationary stochastic model of earthquake motion [J]. Jouenal of the Engineering Mechanics Division, ASCE, 1968, 94(2): 559-583.

[7] SHINOZUKA M, SATO Y. Simulation of non-stationary random process [J]. Journal of the Engineering Mechanics Division, ASCE, 1967, 93(1): 11-40.

[8] IYENGAR R N, IYENGAR K T S R. A non-stationary random process for earthquake accleration [J]. Bulletin of the Seismological Society of America, 1968, 59(3): 1163-1188.

[9] GOTO H, TOKI K. Structural response to non-stationary randomexcitation [C]//Proc. Fourth. World Conference on Earthqukae Engineering,Santiago, Chile, 1969: 130-144.

[10] FANG T, ZHANG T S. Non-stationary mean square response due to uniformly amplitude modulated random excitations [J]. Journal of Sound & Vibration,1995, 182(3): 369-379.

[11] 李创第，邹万杰，黄天立，等. 结构在水平与竖向地震同时作用的非平稳响应[J]. 土木工程学报，2005，38(6)：25-34.

LI Chuangdi, ZOU Wanjie, HUANG Tianli, et al. Non-stationary random response of structures to horizontal-vertical earthquake excitations [J]. China Civil Engineering Journal, 2005, 38(6): 25-34.

[12] PARK S W. Analytical modeling of viscoelastic dampers for structural and vibration control [J]. International Journal of Solids and Structures, 2001, 38: 8065-8092.

[13] CHANG T S, SINGH M P. Mechanical model parameter for viscoelastoc dampers [J]. Journal of Engineering Mechanics, 2009, 135(6): 581-584.

[14] YAMADA K. Dynamic charateristics of SDOF structure with Maxwell element [J]. Journal of Engineering Mechanics, 2008, 134(5): 396-404.

[15] PALMERI A, RICCIARDELLI F. State space formulation for linear viscoelastic system with memory [J]. Journal of Engineering Mechanics, 2003, 129(7): 715-724.

[16] SINGH M P, VERMA N P. Seismic analysis and design with Maxwell dampers [J]. Journal of Engineering Mechanics, 2003, 129(3): 273-282.

[17] PALMERI A. Correlation cofficients for structures with viscoelastic dampers [J]. Engineering Structures, 2006, 28: 1197-1208.

[18] QIAN D, HANSEN J S. A time domain substructure synthesis method for viscoelastic structure [J]. Journal of Applied Mechanics, 1995, 62: 407-414.

[19] 刘延柱，陈文良，陈立群. 振动力学[M]. 北京：高等教育出版社，1998.

[20] 方同，薛璞. 振动理论及应用[M]. 西安：西北工业大学出版社，2000.

Response analysis of energy dissipation structures with Maxwell dampers under non-stationary seismic excitation

LI Chuangdi1, LI Tun1, WEI Xiaoteng2, GE Xinguang1, ZOU Wanjie1

(1. Department of Civil Engineering, Guangxi University of Science and Technology, Liuzhou 545006, China；2. Department of Civil Engineering, Guangxi University, Nanning 530004, China)

Non-stationary random seismic responses of a SDOF structure with generaliged Maxwell dampers and a MDOF structure with Maxwell dampers were studied systematically. The closed-form exact relationships among eigenvalues and eigenvectors of both systems in a structural extended state space and an original space were established, the exact solutions to displacement and velocity of energy dissipation structures and force of dampers were expressed using the system’s eigenvalues and eigenvectors in structural original space. Then, under seven kinds of classical amplitude uniformly modulated white noise seismic excitations and two kinds of classical amplitude uniformly modulated filtered white noise seismic excitations, the exact non-stationary mean-square response solutions to displacement and velocity and damper force of energy dissipation structures were obtained, respectively they were also expressed with eigenvalues and eigenvectors of the system in structural original space, so the analytical methods of exact non-stationary seismic response solutions for and samper force dissipation structures with Maxwell dampers based on analysis of eigenvalues and eigenvectors in their structural original space were established.

Maxwell dampers; energy dissipation structures; forced response of dampers; non-stationary random process; analytical solutions

国家自然科学基金项目(51468005;51368008)；广西自然科学基金项目(2014GXNSFAA118315)；广西科技大学创新团队支持计划

2015-03-19 修改稿收到日期：2015-09-23

李创第 男，博士，教授，1964年生

TU313.3

A

10.13465/j.cnki.jvs.2016.19.029