轴向运动梁在轴向载荷作用下的动力学特性研究
2016-11-23陈红永李上明
陈红永, 李上明
(中国工程物理研究院 总体工程研究所,四川 绵阳 621999)
轴向运动梁在轴向载荷作用下的动力学特性研究
陈红永, 李上明
(中国工程物理研究院 总体工程研究所,四川 绵阳 621999)
研究了轴向运动Timoshenko梁在轴向载荷作用下的振动特性。首先通过考虑轴向拉压载荷作用,根据Timoshenko梁理论和Hamilton原理建立了梁的横向振动控制微分方程,推导了简支-简支边界条件下的梁的无量纲频率随轴向载荷的变化关系,采用新的无量纲化形式消除了无载荷作用下控制方程的奇异性。通过微分求积法进行数值求解并对结果进行验证,分析结果表明:无载荷作用下,长细比越大,越易达到失稳状态;在相同运动速度下,受压状态时比受拉状态下更易达到失稳;临界速度随着轴向载荷的绝对值的增大而减小。通过研究探索了影响临界速度和临界载荷的因素以及两者的关系,对于轴向受载运动系统设计具有一定指导意义。
轴向运动Timoshenko梁;轴向载荷;横向振动;微分求积法
轴向运动系统在工业生产领域有着广泛的应用,比如在生产过程中的传送带、磁带、带锯等,这些结构很多可以简化为轴向运动梁模型,研究轴向运动梁模型的横向振动特性和动力学行为,具有重要的工程实际意义。
对轴向运动系统的研究已经有很多[1-11],以前多采用基于欧拉-伯努利梁理论建模,对于长细比较低的梁模型来说并不精确,因为它忽略了剪切变形和截面转动惯量的影响。SIMPSON[12]第一次引入了剪切效应,采用了特征值方法分析了固支条件下的轴向运动Timoshenko梁的自振频率,并且发现了分叉现象的出现。TANG等[13]采用复模态方法分析了不同边界条件下的轴向受拉的运动Timoshenko梁的自振频率、模态以及临界速度,这些研究对于载荷对自振频率的影响并没有进行深入探讨。对于轴向受压梁的研究相对较少。BOKAIAN[14-15]研究了轴向受拉、压作用对静态Euler梁的影响。POURTAKDOUST等[16]研究了推力对于柔性制导导弹的自振特性影响,这些研究都是针对静态梁,并没有考虑轴向运动效应。GHAYESH等[17]采用多尺度法通过引入转动惯量和温度效应研究了轴向运动梁的非线性横向振动,王波[18]也采用多尺度法研究了运动三参数黏弹性梁的弱受迫振动,李成等[19]考察了非局部参数对固支和悬臂边界条件下超薄梁的固有频率和临界速度的影响。Garlerkin法也被用于分析轴向运动的稳定性[20-21],GUO等[22]等采用微分求积法(DQM)研究了轴向运动热弹耦合梁的振动特性,相比于其它方法,微分求积法具有收敛快计算量小的优点。这些研究中同样只考虑了模型受拉的情况或者完全没有考虑轴向载荷的作用。
本文首先根据Timoshenko梁理论和Hamilton原理得到了轴向运动梁在是否考虑轴向载荷的情况下不同的控制方程,接着采用数值方法求解了其无量纲固有频率并进行了验证,通过分析结构长细比、轴向载荷系数以及轴向运动速度对系统的稳定性的影响。
1 控制方程及边界条件
1.1 轴向受载梁的控制方程
不考虑纵向和横向耦合,梁的动能由横向振动动能,截面转动动能及刚体运动动能构成:
(1)
势能包括轴向力做功、弯曲应变能和剪切应变能:
(2)
根据Hamilton原理[23]
(3)
式中:V(T)为梁的运动速度,N为轴向拉力,梁的横向振动位移W(X,T),梁的截面刚度为EI,剪切刚度为κGA(κ为截面剪切系数),截面转动惯量为ρI,梁长度为L,单位长度的质量为ρA。Θ表示梁截面转角,对Timoshenko梁模型,Θ=∂W/∂X+Ψ,Ψ为纯剪切产生的剪切角。
将式(1)和(2)代入式(3)求解变分,不考虑轴力对轴向坐标和时间的导数,仅保留速度和加速度项,由于变分项的任意性,变分项系数为0,则可得均匀梁的横向振动方程为:
(4)
(5)
式中:梁所受的弯矩和剪力为:
(6)
由式(4)可得:
(7)
将式(7)代入式(5),可得仅包含横向振动的控制方程为:
(8)
式中,下标X和T分别表示对轴向坐标X和时间T的导数。根据上述推导过程,同理可得受压梁的控制方程。根据参数关系,将式(8)进行无量纲化处理:
(9)
4k2vvtwxxt+5k2vtwxtt+k1vtwxxx+
(k4+δk1-k1v2)wxxxx-2k1vwxxxt-
(k1+k3+δk2-k2v2)wxxtt+
2k2vwxttt+k2wtttt=0
(10)
式中:k1、k2及k5包含剪切模量,表征剪切刚度,k3和k4分别表征扭转系数及弯曲刚度;δ为载荷系数:
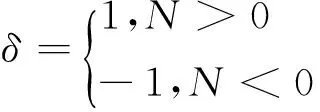
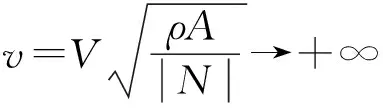
为了消除这种奇异性的影响,对无载荷作用的情况进行单独分析。
1.2 无轴力作用控制方程
定义新的无量纲参数定义为
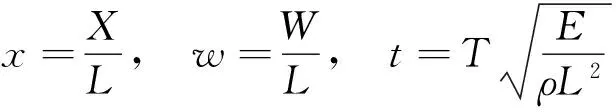
(11)
vt′wx+wtt+2v′wxt+v′2wxx+
4k1v′vt′wxxt+5k1vt′wxtt+k1vt′wxxx+
(k3-k1v′2)wxxxxx-2k1v′wxxxt-
(k1+k3-k1v′2)wxxtt+2k1v′wxttt+k1wtttt=0
(12)
若不考虑轴向运动速度,则相当于求解方程:
wtt+wxx+k3wxxxx-
(k1+k3)wxxtt+k1wtttt=0
(13)
简支-简支边界条件可表示为:
(14)
2 求解方法及验证
2.1 基于DQM方法的控制方程求解方法
文中采用DQM方法进行控制方程式(10)及式(12) 的求解,求解主要过程如下:
根据微分求积法(DQM)[24],函数在某点的r阶导数的值可以表示为在所有节点上函数值的加权和的形式:
(15)
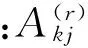
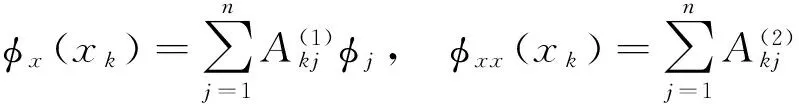
(16)
采用不均匀网格点进行划分,为了处理高阶边界条件,引入δ方法在两端节点处增加距离端点δL(约为10-4~10-6)两个网格点,并重新编号:
x1=0,x2=δL,xn-1=1-δL,xn=1
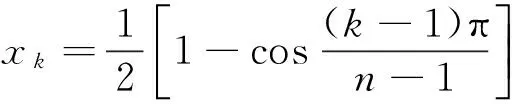
k=3,4…,n-2
(17)
根据插值原理,采用Lagrange多项式确定权系数,
(18)
高阶权系数可以用以下关系来确定
(19)
则将式(12)~(16)代入控制方程式(8)和式(9)可得:
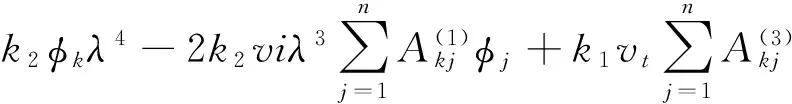

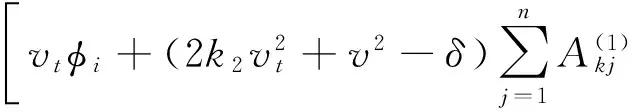
(20)
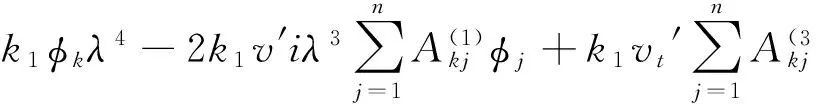
(21)
通过将简支-简支边界条件以相同方法引入,可以将式(20)和式(21)转化为矩阵形式为
(B(4)λ4+B(3)λ3+B(2)λ2+
B(1)λ+B(0))Φ=0
(22)
式中:B(p),p=0,1,2,3,4都为n阶方阵,Φ=[φj]T,j=1,2,…,n。式(18)变为四阶广义特征值求解问题,求解方程的广义特征值即能得到无量纲频率值。
2.2 数值方法验证
轴向受载静态Euler梁的无量纲化控制方程为:
wxxxx-δwxx/k4-λ2w=0
(23)
根据轴向载荷与临界压力载荷的比值定义载荷系数为:
(24)
式中:μ为边界条件系数,简支-简支梁μ=π2。用数值寻根方法求解轴向受载梁的特征方程可以得到前4阶特征值λ随轴向压力系数kN的变化,如图1所示。
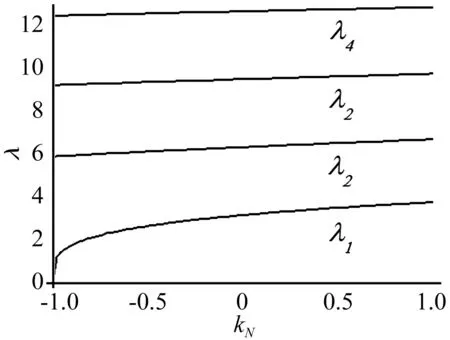
图1 简支-简支梁前四阶特征值随载荷系数的变化Fig.1 The first four order eigenvalues of pinned-pinned beam VS. load factor
取载荷系数kN=-1~1,即载荷从临界压力到一倍于临界压力值的拉力状态。从图1中可以看出,各边界条件下各阶特征值都随轴向载荷变大而变大,是因为轴向压力变小和拉力变大都使得结构刚度变大,其横向弹性振动频率变大。不同的是第二、三和四阶特征值随载荷增大缓慢变大,而第一阶特征值当载荷接近临界载荷即kN=-1~11时迅速从0增大且变之后增速平缓。同时可以看出,当到达临界压力载荷时第一阶弹性振动固有频率降为0,达到失稳状态。当有轴力作用时,根据无量纲化关系,可以得到无量纲频率与系统原始固有频率的关系:
(25)
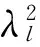
对DQM方法计算得到的无轴向运动速度情况下简支-简支梁的前三阶无量纲频率进行对比,根据Timoshenko给出的近似关系,可以将简支-简支边界条件下的无量纲固有频率根据式(25)转化为相应的Timoshenko梁的无量纲频率[25],并进行比较。结果如表1所示。
(26)
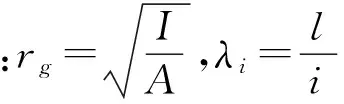
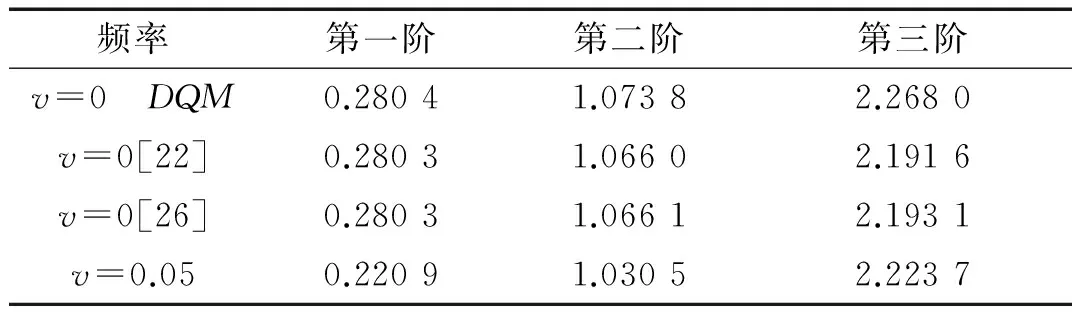
表1 无轴力情况下计算结果验证
对于考虑轴力作用的情况,根据式(22)所得的无量纲特征值,通过特征值与无量纲频率之间的关系(25)式进行相应转化,可以得到解析解与DQM解的对比关系,如图2所示。
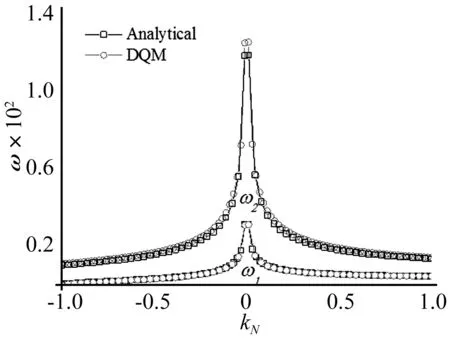
图2 解析法与DQM方法求解简支-简支梁前两阶无量纲频率的结果对比v=0Fig.2 Comparison of first two order natural frequencies of Analytical and DQM for pinned-pinned beam
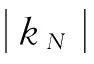
3 数值算例讨论
图3给出了简支-简支边界条件下前3阶无量纲频率与运动速度的关系,以及前两阶固有频率与载荷系数的关系。其中图3(a)给出了无轴力情况下,不同长细比的梁前三阶固有频率随速度下降,当长细比从5变大到10时,前三阶频率都下降,一阶频率失稳的无量纲速度v′ 从0.174降低到0.091。可见无轴力情况下,结构长细比对固有频率影响很大。
图3(b)中给出了当运动梁受到0.1和0.5倍临界载荷的拉力和压力情况下,前三阶固有频率随速度的变化。可以看出当压力和拉力绝对值相等时,无量纲固有频率相差较小,拉力大于压力,对于一阶频率这种差别当轴向载荷更大时更加明显。简支-简支梁0.5倍拉力时临界速度为1.7,0.5倍压力时临界速度降低为1.0。可见轴向载荷值较大时,对一阶频率影响明显。
图3(c)中给出了前两阶固有频率在不同速度下与轴向载荷的关系。当运动梁受到压力作用时,与轴向运动效应耦合,会使得动态失稳点提前。表现为一阶固有频率降低为0,当载荷继续增大之后与2阶固有频率耦合,出现耦合模态颤振现象。当运动速度从0~3变大,简支-简支梁的临界载荷由原来的1倍临界载荷变为0.2倍。对于受拉力的情况下,也会出现失稳状态,也会出现像压力状态下的1阶频率降为0之后与2阶耦合的情况,简支-简支梁在0.35处出现失稳,但是在1倍拉力内未出现耦合现象。

图3 简支-简支梁无量纲频率与运动速度及载荷系数的关系Fig.3 The dimensionless complex frequencies vs. speed and load for pinned-pinned beam
4 结 论
通过推导轴向运动Timoshenko梁在有无轴向载荷作用下的控制方程,用数值求解方法求解并给出了简支梁轴向载荷和运动速度对梁模型固有频率的影响,分析了临界速度与载荷的关系,可以总结出如下结论:
(1) 无载荷作用下,梁模型长细比越大,越易达到失稳状态。
(2) 简支梁固有频率都随着轴向载荷及轴向运动速度的增大而减小;在相同运动速度下,受压状态时比受拉力作用下更易达到失稳状态。
(3) 临界速度随着轴向载荷的绝对值的增大而减小。
[1] MOTE C D. A study of band saw vibrations [J]. Journal of the Franklin Institute,1965, 279: 430-444.
[2] WICKERT J A. Non-linear vibration of a traveling tensioned beam[J]. International Journal Non-Linear Mechanics,1992, 27: 503-517.
[3] HUANG J L, SU R K L, LI W H, et al.Stability and bifurcation of an axially moving beam tuned to three-to-one internal resonances[J]. Journal of Sound and Vibration,2011,330(3):471-485.
[4] CHEN L Q, TANG Y Q, LIN C W. Dynamic stability in parametric resonance of axially accelerating viscoelastic Timoshenko Beam[J]. Journal of Sound and Vibration, 2010,329(5):547-565.
[5] DING H, CHEN L Q. Galerkin methods for natural frequencies of high-speed axially moving beams[J], Journal of Sound and Vibration,2010, 329(17):3484-3494.
[6] DING H, ZHANG G C, CHEN L Q. Supercritical equilibrium solutions of axially moving beams with hybrid boundary conditions[J]. Mechanics Research Communications,2011, 38(1):52-56.
[7] GHAYESH M H. Nonliear forced dynamics of an axially moving viscoelastic beam with an internal resonance[J]. International Journal of Mechanical Sciences,2011,53(11):1022-1037.
[8] GHAYESH M H, KAFIABAD H A, REID T. Sub- and super-critical nonlinear dynamics of a harmonically excited axially moving beam[J]. International Journal of Solids and Structures, 2012, 49(1):227-243.
[9] GHAYESH M H. Coupled longitudinal-transverse dynamics of an axially accelerating beam[J]. Journal of Sound and Vibration, 2012,331:5107-5124.
[10] GHAYESH M H. Subharmonic dynamics of an axially accelerating beam[J]. Archive of Applied Mechanics, 2012,82: 1169-1181.
[11] GHAYESH M H, AMABILI M. Steady-state transverse response of an axially moving beam with time-dependent axial speed[J]. International Journal of Non-Linear Mechanics, 2013, 49: 40-49.
[12] SIMPSON A. Transverse modes and frequencies of beams translating between fixed end supports[J].Journal of Mechanical Engineering Science, 1973, 15: 159-164.
[13] TANG Y Q, CHEN L Q, YANG X D. Natural frequencies modes and critical speeds of axially moving Timoshenko beams with different boundary conditions[J].International Journal of Mechanical Sciences, 2008, 50: 1448-1458.
[14] BOKAIAN A. Natural frequencies of beams under compressive axial loads[J]. Journal of Sound and Vibration,1988, 126: 49-65.
[15] BOKAIAN A. Natural frequencies of beams under tensile axial loads[J]. Journal of Sound and Vibration,1990, 142:481-498.
[16] POURTAKDOUST S H, ASSADIAN N. Investigation of thrust effect on the vibrational characteristics of flexible guided missiles[J].Journal of Sound and Vibration,2004, 272: 287-299.
[17] GHAYESH M H, KHADEM S E. Rotary inertia and temperature effects on non-linear vibration, steady-state response and stability of an axially moving beam with time-dependent velocity[J]. International Journal of Mechanical Sciences, 2008, 50: 389-404.
[18] 王波. 轴向运动三参数黏弹性梁弱受迫振动的渐近分析[J].应用数学和力学,2012,33(6):771-780.
WANG Bo. Asymptotic analysis on weakly forced vibration of an axially moving viscoelastic beam constituted by standard linear solid model[J]. Applied Mathematics and Mechanics, 2012,33(6):771-780.
[19] 李成,姚林泉. 轴向运动超薄梁的非局部动力学分析[J].工程力学, 2013, 30(4): 366-372.
LI Cheng, YAO Linquan. Nonlocal dynamical analysis on axially travelling ultra-thin beam [J].Engineering Mechanics,2013, 30(4): 366-372.
[20] 张能辉,王建军,程昌钧. 轴向变速运动黏弹性弦线横向振动的复模态Galerkin方法[J]. 应用数学和力学,2007, 28(1): 1-8.
ZHANG Nenghui, WANG Jianjun, CHENG Changjun. Complex mode galerkin approach in transverse vibration of an axially accelerating viscoelastic string[J].Applied Mathematics and Mechanics, 2007, 28(1): 1-8.
[21] 陈红永,陈海波, 张培强. 轴向受压运动梁横向振动特性的数值分析[J].振动与冲击,2014,33(24): 101-105.
CHEN Hongyong, CHEN Haibo, ZHANG Peiqiang. Numerical analysis of free vibration of an axially moving beam under compressive load [J]. Journal of Vibration and Shock, 2014, 33(24): 101-105.
[22] GUO X X, WANG Z M, WANG Y, et. al. Analysis of the coupled thermoelastic vibration for axially moving beam[J].Journal of Sound and Vibration, 2009, 325: 597-608.
[23] 邱吉宝,向树红,张正平. 计算结构动力学[M]. 合肥:中国科学技术大学出版社, 2009: 31-33.
[24] SUNG K J, CHARLES W B, ALFRED G S. Application of differential quadrature tostatic analysis of structural components [J].International Journal for Numerical Methods in Engineering, 1989, 28: 561-577.
[25] TIMOSHENKO S, YOUNG D H, WEAVER W. Vibration problems in engineering [M]. New York: John Wiley & Sons. Inc. Forth Edition. 432-434.
[26] SUN Y X, FANG D N, AI S K. Thermalelastic damping in micro-beam resonators [J]. International Journal of Solids and Structures,2006, 43: 3213-3229.
Dynamic characteristics of an axially moving Timoshenko beam under axial loads
CHEN Hongyong, LI Shangming
(Institute of Systems Engineering, CAEP, Sichuan 621999, China)
The effects of axial load on vibration characteristics of an axially moving Timoshenko beam were investigated. The governing differential equation for transverse vibration of the axially moving beam under axial load was established based on Timoshenko beam theory and Hamilton’s principle. The dynamic characteristics of the beam under axial load and pinned-pinned boundary conditions were investigated. The dimensionless frequencies of the beam versus axial load were calculated numerically using the differential quadrature method (DQM), and they were compared with the analytical solutions for verification. The results showed that under the condition of no load, the larger the slendness ratio of the beam, the easier the beam reaches unstable state; the beam reaches unstable state easier under compressive load than it does under tensile load; the critical speed of the beam decreases with increase in the absolute value of axial load. Through studying the influence factors and the relationship between the critical speed and the critical load of the beam, the results provided a guid for the design of axially moving systems under axial load.
axially moving Timoshenko beam; axial load; transverse vibration; differential quadrature method
国家自然科学基金面上项目(11272299)
2015-06-15 修改稿收到日期:2015-09-22
陈红永 男,博士,助理研究员,1986年5月生
李上明 男,博士,副研究员,1978年7月生
O32
A
10.13465/j.cnki.jvs.2016.19.013
