转子/机匣碰摩引起的转子弯扭耦合振动

2016-11-23廖明夫宋明波张霞妹

振动、测试与诊断 2016年5期

关键词：轴心机匣阻尼

廖明夫, 宋明波，张霞妹

(西北工业大学动力与能源学院西安,710072)

转子/机匣碰摩引起的转子弯扭耦合振动

廖明夫, 宋明波，张霞妹

(西北工业大学动力与能源学院西安,710072)

以航空发动机为研究背景，针对其转子/机匣间隙小，转速控制存在延迟，碰摩故障发生可能导致的发动机转子弯扭耦合振动的特征，建立了计及陀螺力矩的弹性支承-柔性转子-弹性静子系统的碰摩故障模型，模型中考虑了有延迟的转速控制力矩。采用延迟微分方程的数值积分方法对方程进行了数值分析。分析结果表明：碰摩作用发生时，剧烈的碰摩会导致转子的反进动，而碰摩与转速控制力矩的延迟共同作用会导致转子的扭转振动加剧，甚至可能发生扭振失稳。应当在发动机控制系统的设计中充分考虑这种转子动力学影响。同时，发动机扭振信号也可以作为转子/机匣发生碰摩的重要诊断信息之一。

航空发动机；转子；转静碰摩；弯扭耦合振动；失稳

引言

转子/机匣碰摩是航空发动机运行过程中常见的现象，在某些情况下会造成发动机的进一步故障。因此，转/静子碰摩成为发动机振动研究的焦点之一，备受关注[1]。近年来，国内外学者分别在动力学建模[2-4]、摩擦模型[5]仿真[6-7]以及实验[8-11]等方面进行了深入探索，但往往忽略了碰摩摩擦力引起的转子扭振以及转速控制力矩[12、13]。邓小文[14-16]以一种异步电机为对象，研究了转、静子的弯曲-扭转耦合振动，该研究针对电机驱动的地面旋转机械，其转速控制响应快，反馈转矩可迅速控制转子的转速。航空发动机通过高压气流与燃油混合燃烧后产生高温燃气作为驱动，转速控制系统的响应要慢得多，而工作转速又非常高，因此，航空发动机的碰摩将可能造成转速波动，引起转子弯扭耦合振动。笔者建立了考虑转子弯扭耦合振动的转子/机匣碰摩模型，引入带延迟的转速控制反馈函数，分析了转子机匣碰摩引起的弯扭耦合振动特性。结果表明，转子机匣碰摩引起的弯扭耦合振动是不能忽视的，在一定的情况下，转子机匣碰摩会造成转子扭转振动失稳。

1 模型及坐标系

图1为本研究分析转子机匣碰摩引起转子弯扭耦合振动的转子-机匣模型。它由两部分组成：转子部分包括一根无质量的弹性轴和一个存在不平衡偏心ε的转盘，质量为m，极转动惯量为Jp，直径转动惯量为Jd，支承于两个弹性支承上，其刚度系数、阻尼系数分别为：sb1,sb2,db1,db2；静子部分模拟机匣，质量为mst、刚度为sst，阻尼系数为dst。为了便于研究，假定模型中所有元件均为各向同性。

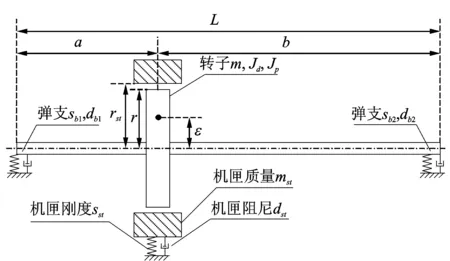
图1 转子-机匣模型Fig.1 The dynamic model of rotor-casing

2 系统运动微分方程

2.1 运动微分方程

在转子/机匣碰摩情况下，受力分析如图2所示。由质心运动定理以及动量矩定理得到转子系统的动力学微分方程为

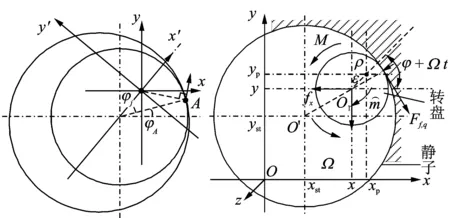
图2 转子-机匣碰摩时的受力分析Fig.2 The force analysis of rotor-casing contact

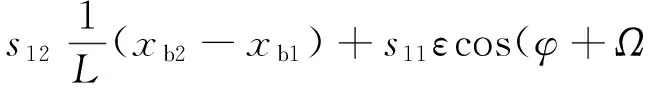
(1)

(6)

(7)

(8)

2.2 转速控制力矩

式(5)中的ΔM为转子的转速控制力矩，当转子以稳定转速Ω运行时，ΔM=0，当转子由于外来干扰导致转速发生变化时，这个控制力矩ΔM则试图抑制转速的变化。

假设转子的转速与力矩有如下的关系

(12)

其中:Q为控制力矩系数，取0.1。

当转速增加ΔΩ时，力矩为

(13)

为了抑制这个转速变化，系统附加一个转速控制力矩ΔM，则

(14)

ΔΩ为微小量，略去高阶小量，得到

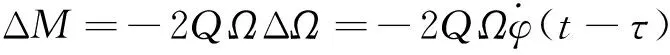
(15)

2.3 碰摩力

1)弹性正碰力

本研究采用Schweitzer碰摩理论，其正碰力F的大小[1,16]描述如下

(16)

当δ≥ 0时，碰摩发生。

2) 摩擦力

(19)

OPC UA的接口主要有两种：一种是自定义接口，即CUSTOM标准接口，是服务商必须提供的，主要用于C++编写的客户程序；而另一种是OLE自动化标准接口，主要用于C#、VB等语言所开发的应用程序。而SINUMERIK 828D数控系统提供了OLE自动化标准接口，同时采用C#在HMI设计中较MFC更具有优势，因此本项目采用了OLE自动化标准接口。

(20)

(22)

(23)

其中

(24)

3 数值求解

3.1 参数取值

仿真计算中模型各参数取值如表1所示。计算得到转子的弯曲临界转速为：1 231.2 r/min，扭转振动临界转速为2 200 r/min。

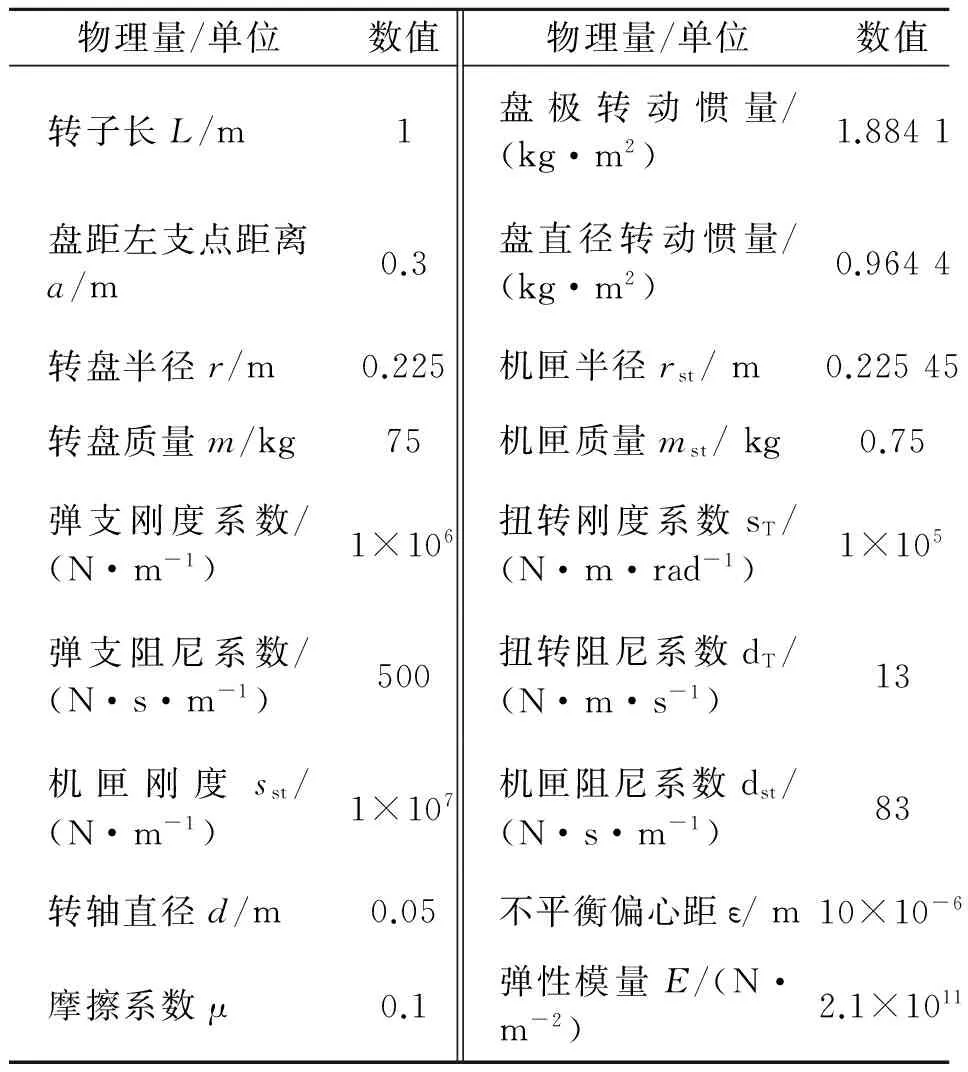
表1 参数取值

3.2 不同转速下的碰摩

假设转子稳态运行过程中，在第2 s时突然发生掉块，导致转子不平衡突然增大，ε由10×10-6m变化为100×10-6m，从而导致碰摩，并设延迟τ为10个周期。

从图3看出，转速处于1 050 r/min时，转子在掉块后发生了轻微的碰摩，这是由于转子在掉块后会发生一个较大的瞬态振动，随后转子进入稳态运行，不再碰摩。1 150，1 300和1 400 r/min 3个转速邻近临界转速，弹性正碰力剧烈。

如图4所示，碰摩将引起转子的扭转振动，1 500 r/min转子发生轻微的碰摩后，进入了稳态运行，转子的扭振逐渐衰减。当转子处于1 150,1 300和1 400 r/min转速时，由于碰摩的持续作用，转子的扭振一直存在，且出现失稳的趋势。这是由于碰摩力矩和转子的转速控制力矩一起作用的结果。

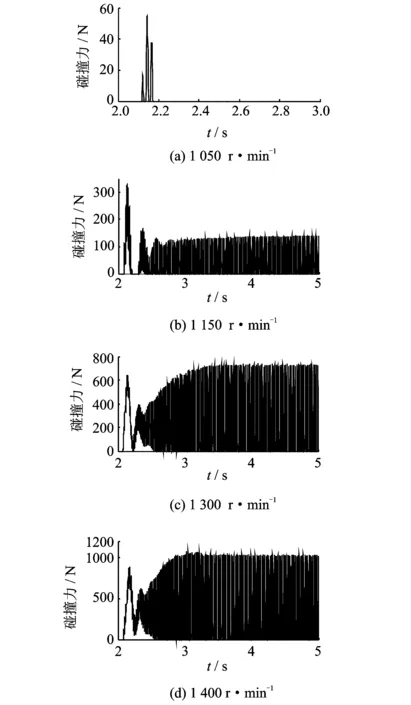
图3 不同转速下的弹性正碰力Fig.3 The impact force at different rotational speed

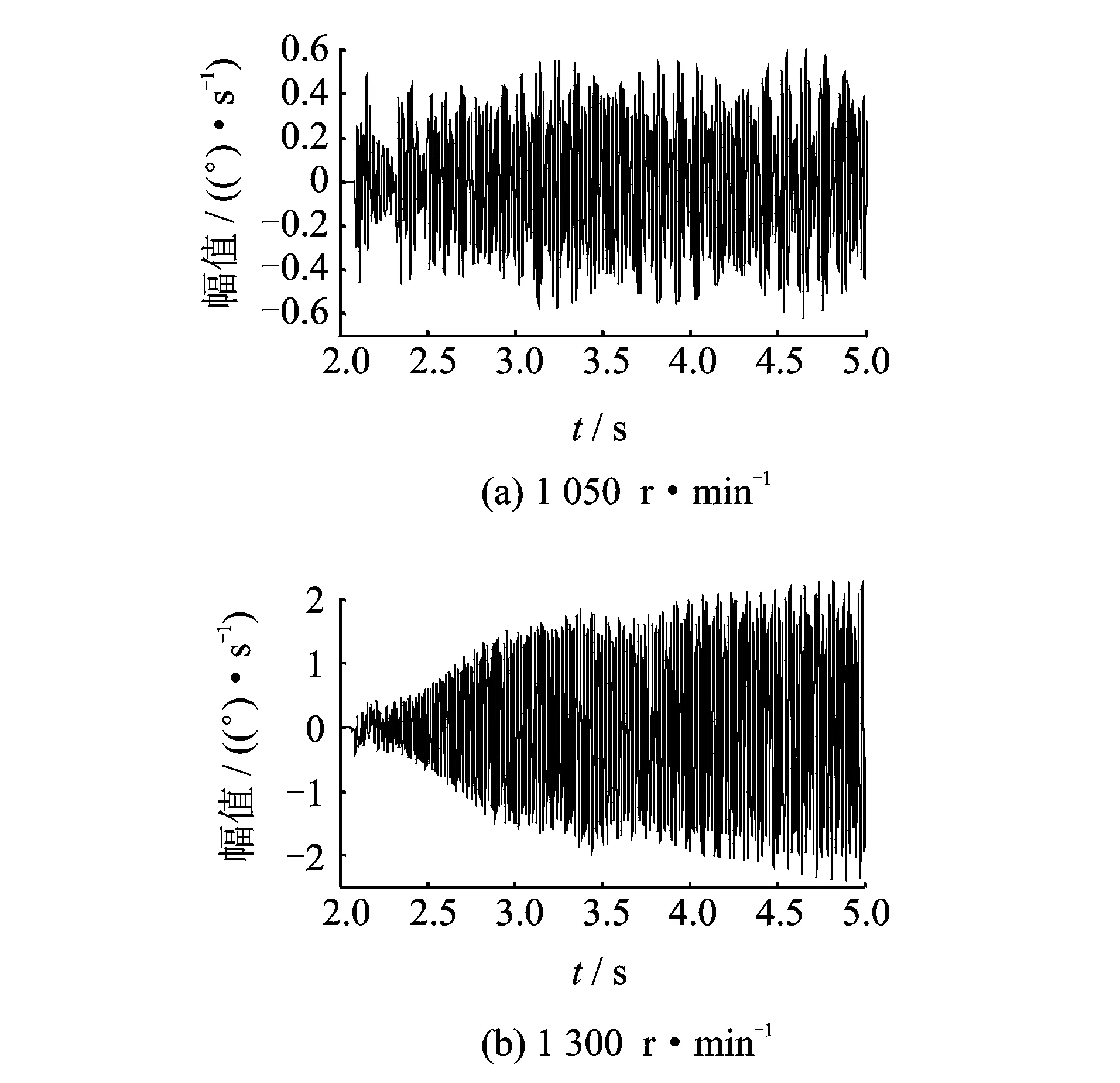
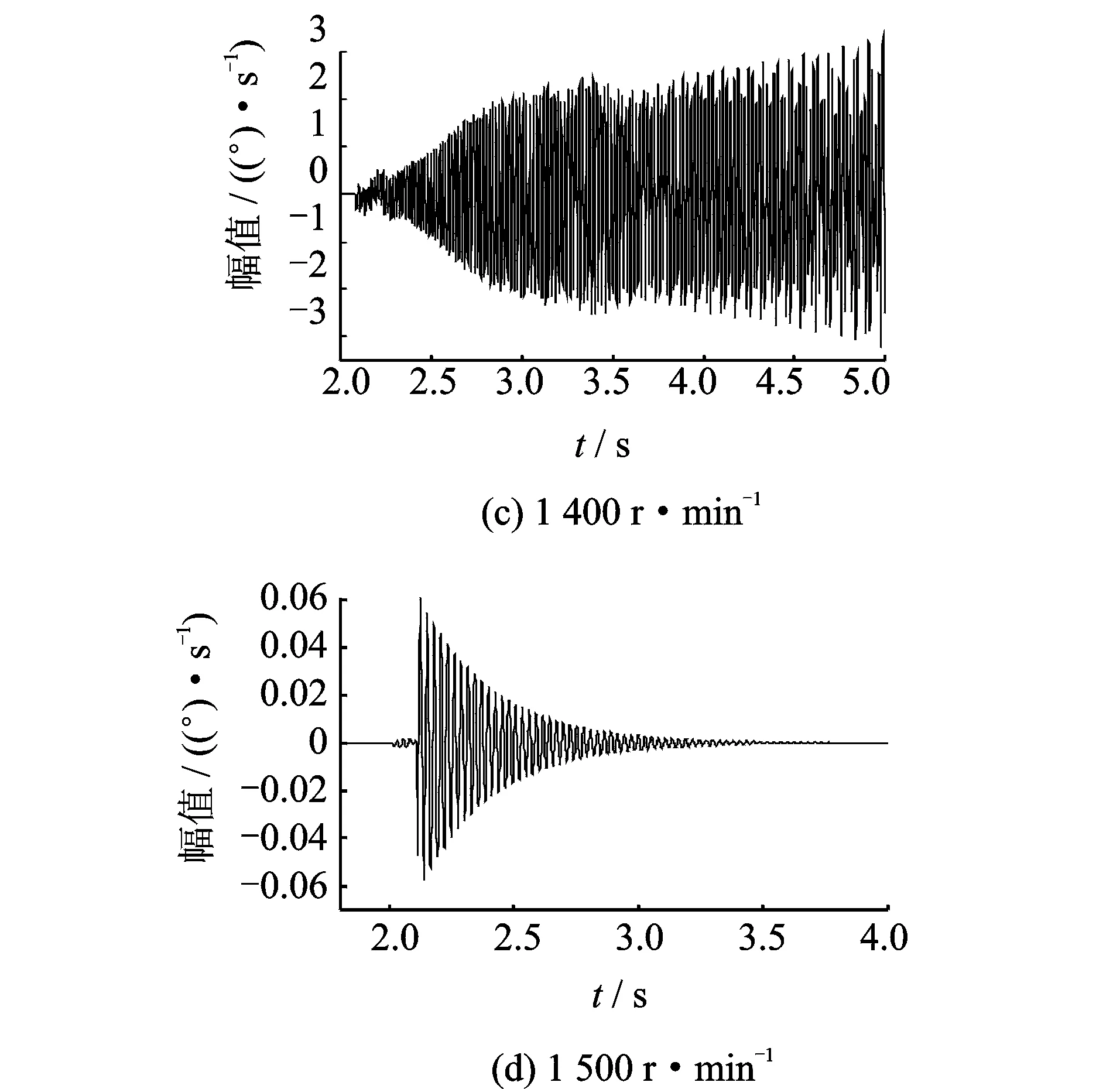
图4 不同转速下转子的扭转振动Fig.4 The torsional vibration at different rotational speed

频率成分始终存在，在轻微碰摩情况下,扭振的频率为扭振自振频率单一频率。而当转子掉块后发生强碰摩，扭振的频率成分复杂，主要表现为弹性正碰力的冲击频率，如图6所示。

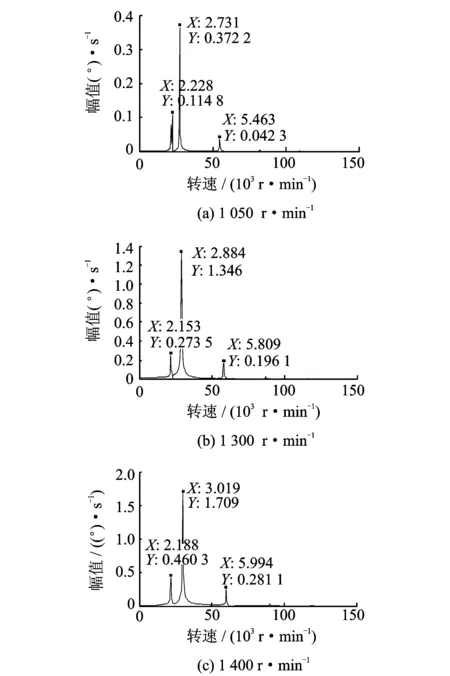
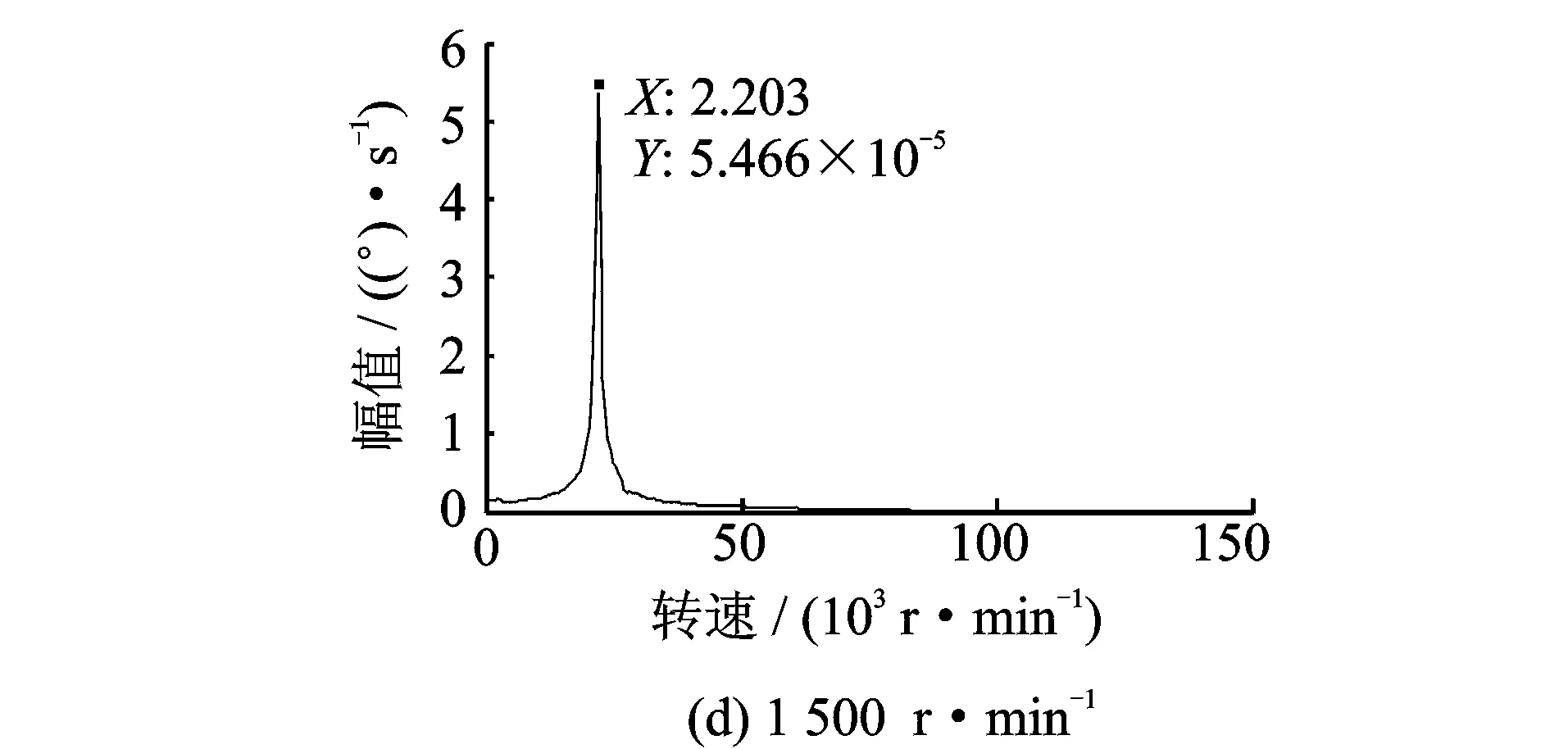
图5 不同转速下转子扭转振动频谱Fig.5 The frequency spectrum at different rotational speed

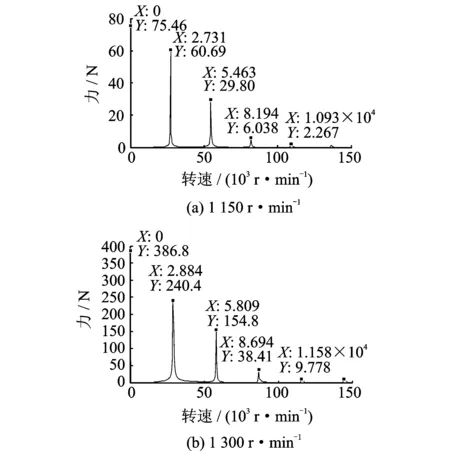
图6 不同转速下弹性正碰力的频谱Fig.6 The frequency spectrum of impact force at different rotational speed

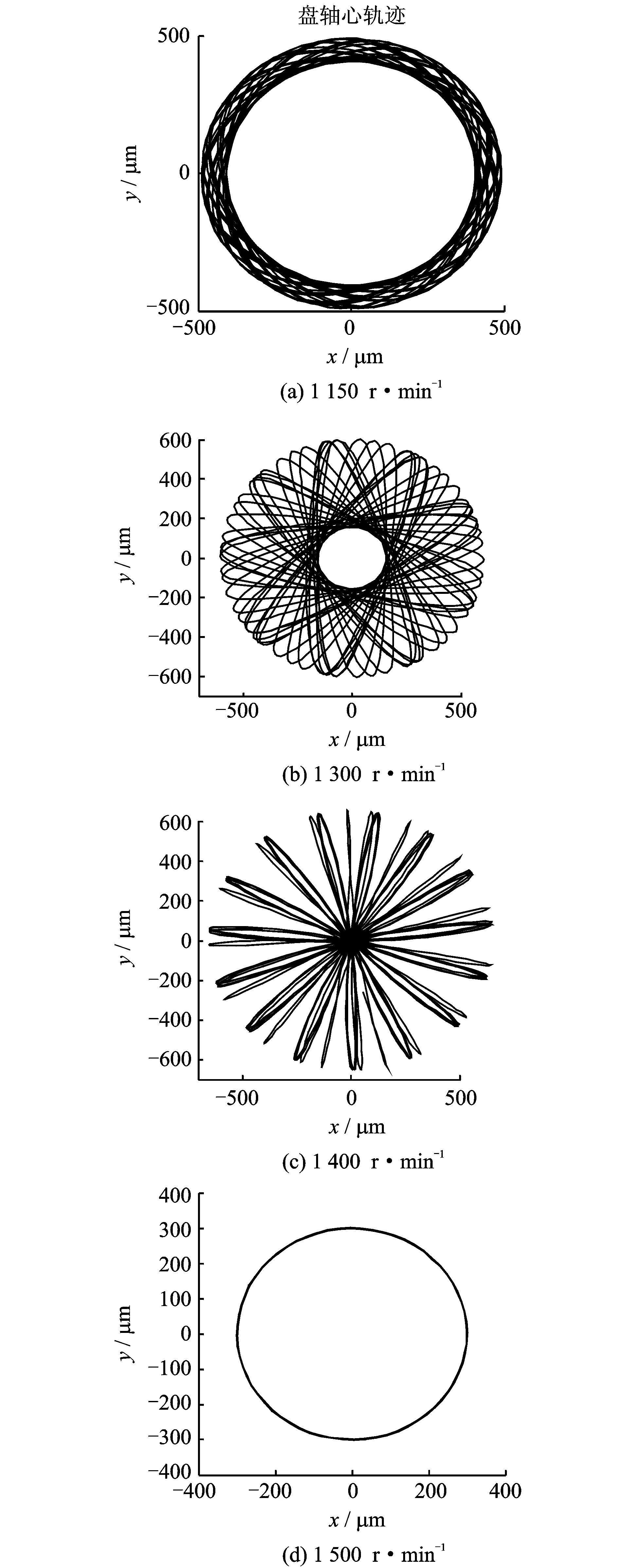
图7 不同转速下转子轴心轨迹Fig.7 The axis orbit at different rotational speed

图7为转子机匣碰摩后的轴心轨迹。转子在1 500 r·min-1发生轻微碰摩后进入稳态运行状态，脱离碰摩，轴心轨迹为一个圆。转子在1 150，1 300和1 400 r·min-1时，轴心轨迹均为花瓣状。当转子在1 400 r·min-1转速下时，碰摩发生初期，碰摩力较小时，转子轴心轨迹与1 150,1 400 r·min-1时类似，但一段时间后，碰摩力稳定在1 000 N左右，转子在机匣之间发生来回震荡，发生了如图所示的轴心轨迹，凸显了系统的非线性特性。

图8为转子振动的进动分析。选取了碰摩发生后的32个周期数据分析，可以看出，在1 050 r·min-1时，由于瞬态响应没有完全衰减，系统除了1×倍频还有自振频率分量。1 150,1 300,1 400 r·min-1均选取了转子由于掉块导致的自振频率振动衰减后的32个周期数据，可以看出，由于碰摩的持续作用，系统出现了反进动。反进动的频率为正碰力的冲击频率与转子转频之差。在1 400 r·min-1时，由于转子在机匣中发生了类似来回震荡的情况，因此反进动较大。

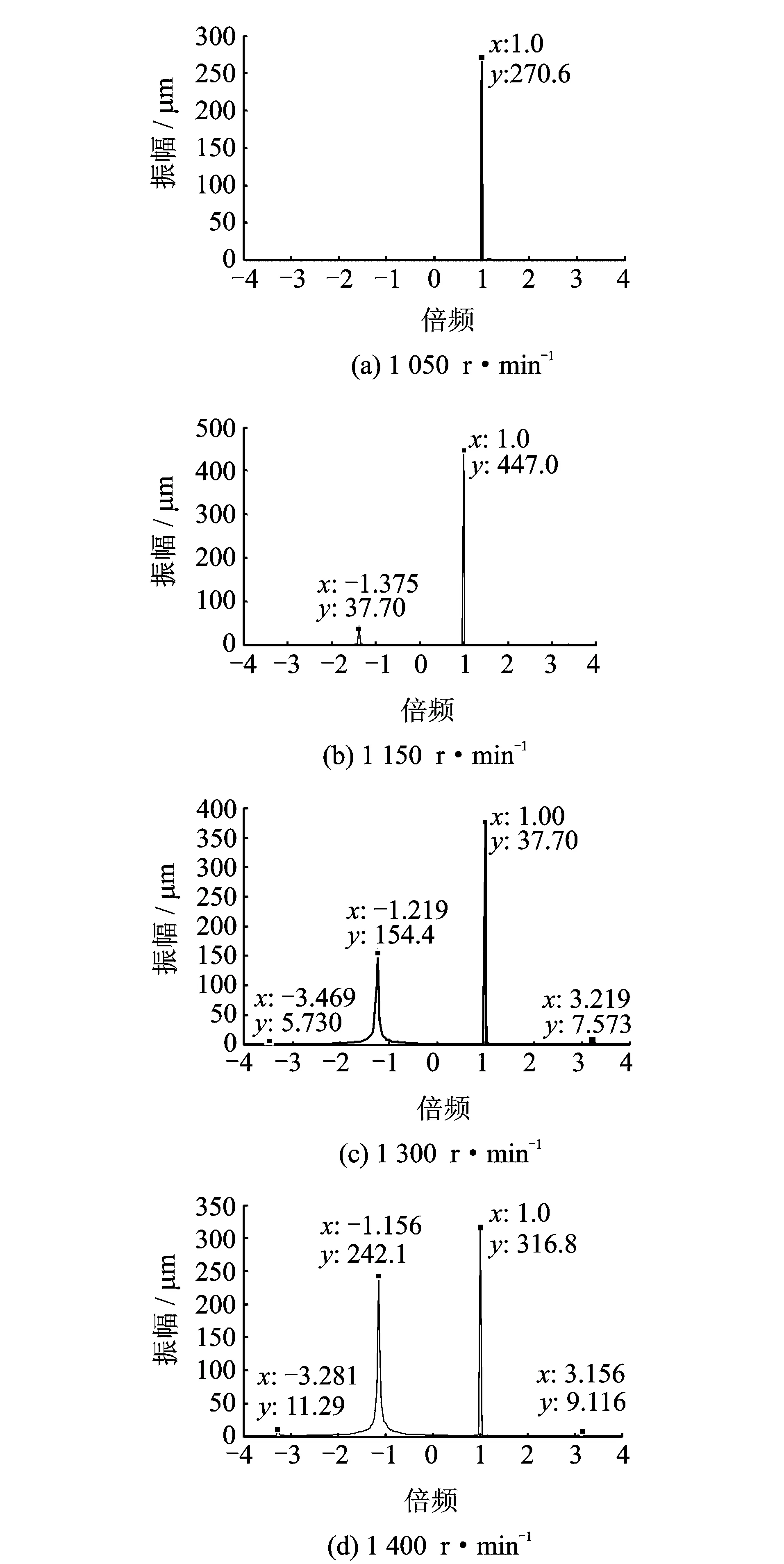
图8 不同转速下转子的进动Fig.8 The whirl transform of rotor vibration at different rotational speed

3.3 不同控制力矩延迟下的扭振

由于控制力矩的延迟，转子可能发生不同状态的振动。控制力矩相当于对系统的扭振提供了附加的阻尼，但如果系统的控制力矩有延迟，则可能导致所提供的阻尼为负阻尼，从而引起扭振失稳。在发动机中转速控制力矩的延迟是不可避免的。

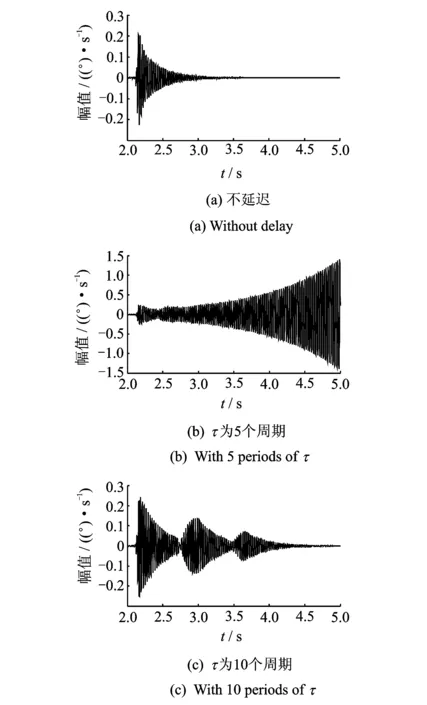
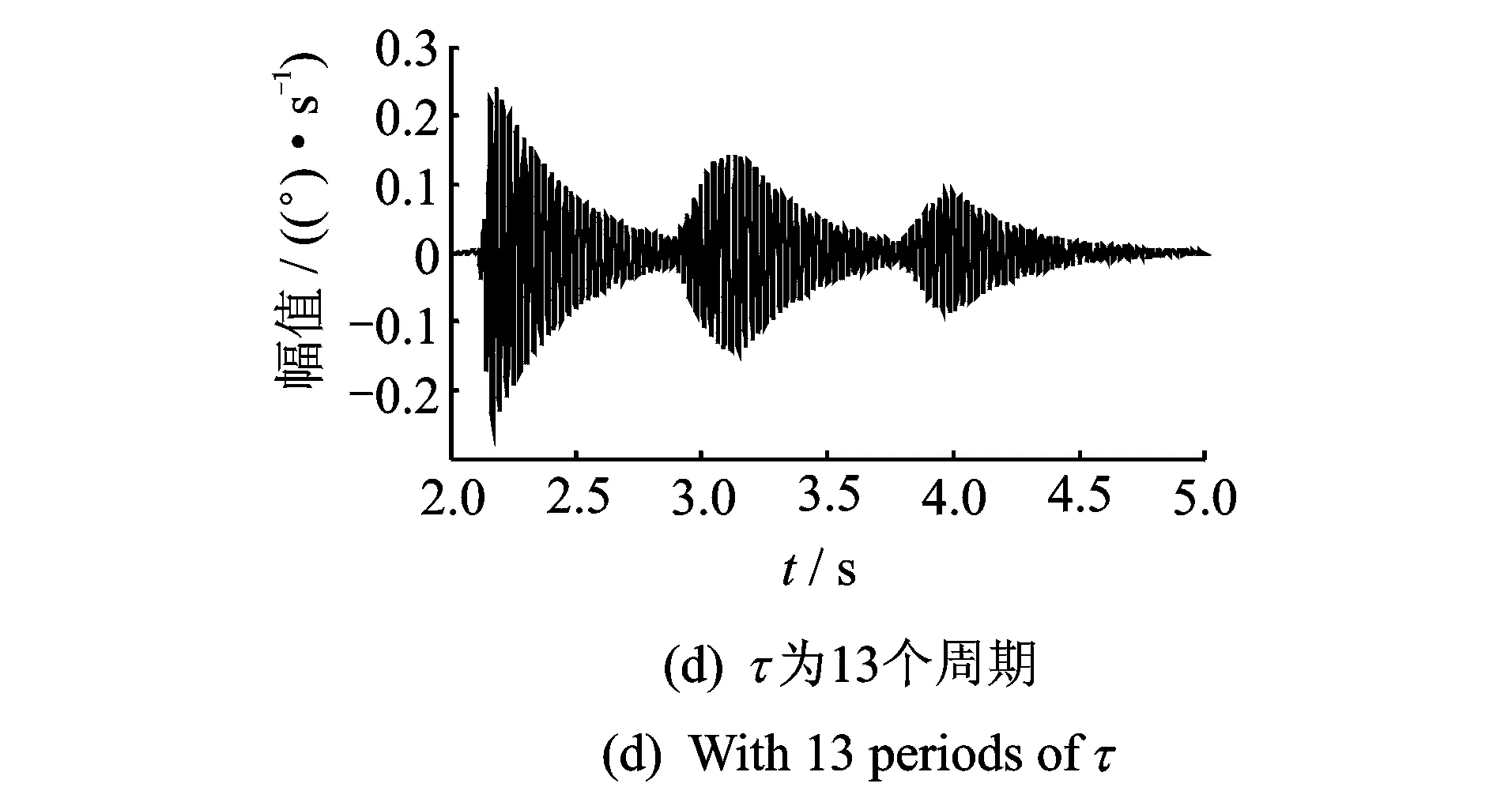
图9 1 050 r/min时不同控制力矩延迟下的扭振Fig.9 The torsional vibration with different control torque at 1 050 r/min

图9为1 050 r·min-1时不同的控制力矩延迟下转子的扭转振动，此时转子机匣发生轻微碰摩。控制力矩的启动门槛值设置为0.1 (°)/s，即只有当转速波动大于0.1 (°)/s时，控制力矩才作用。从图中可以看出，当控制力矩没有延迟时，相当于对系统提供了扭振阻尼，而当控制力矩有延迟时，系统的扭振发生震荡，这正是由于控制力矩对系统提供了负阻尼所致，尤其当延迟为5个旋转周期时，扭振发生了失稳。由此看出，即使发生轻微的碰摩，如果控制力矩施加不当，系统扭振也有失稳的可能。

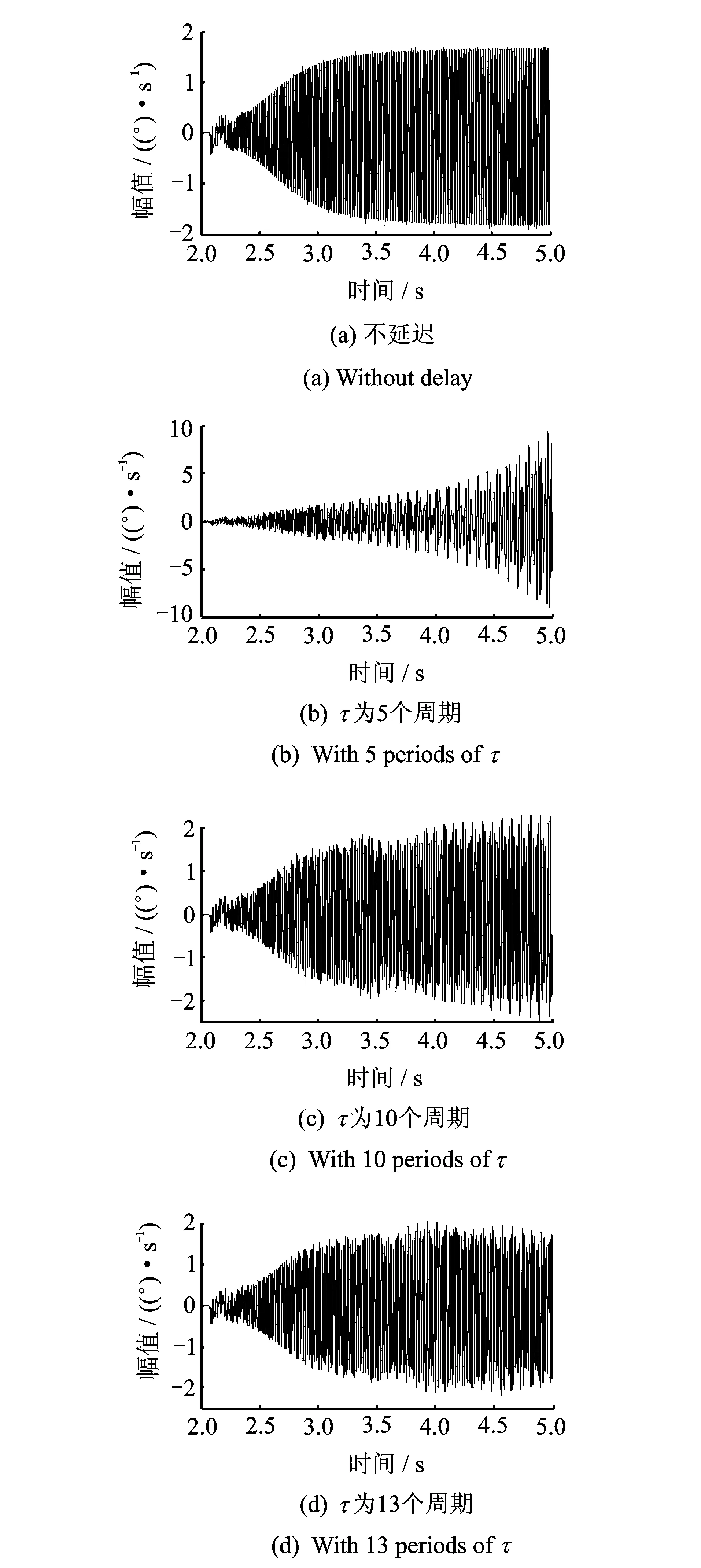
图10 1 300 r·min-1时不同控制力矩延迟下的扭振Fig.10 The torsional vibration with different control torque at 1 300 r·min-1

图10为1 300 r·min-1时不同的控制力矩延迟下转子的扭转振动。此时转子和机匣发生了剧烈的碰摩。同样设置控制力矩的启动门槛值为0.1 (°)/s，即只有当转速波动大于0.1 (°)/s时，控制力矩才作用。从图中可以看出，当控制力矩没有延迟时，相当于对系统提供了扭振阻尼，而当控制力矩延迟为5个旋转周期时，转子出现扭振失稳。这是由于控制力矩延迟产生了负阻尼，而当控制力矩延迟为10个旋转周期以及13个旋转周期时，虽没有发生失稳，但扭振依然持续发生，且幅值较大。

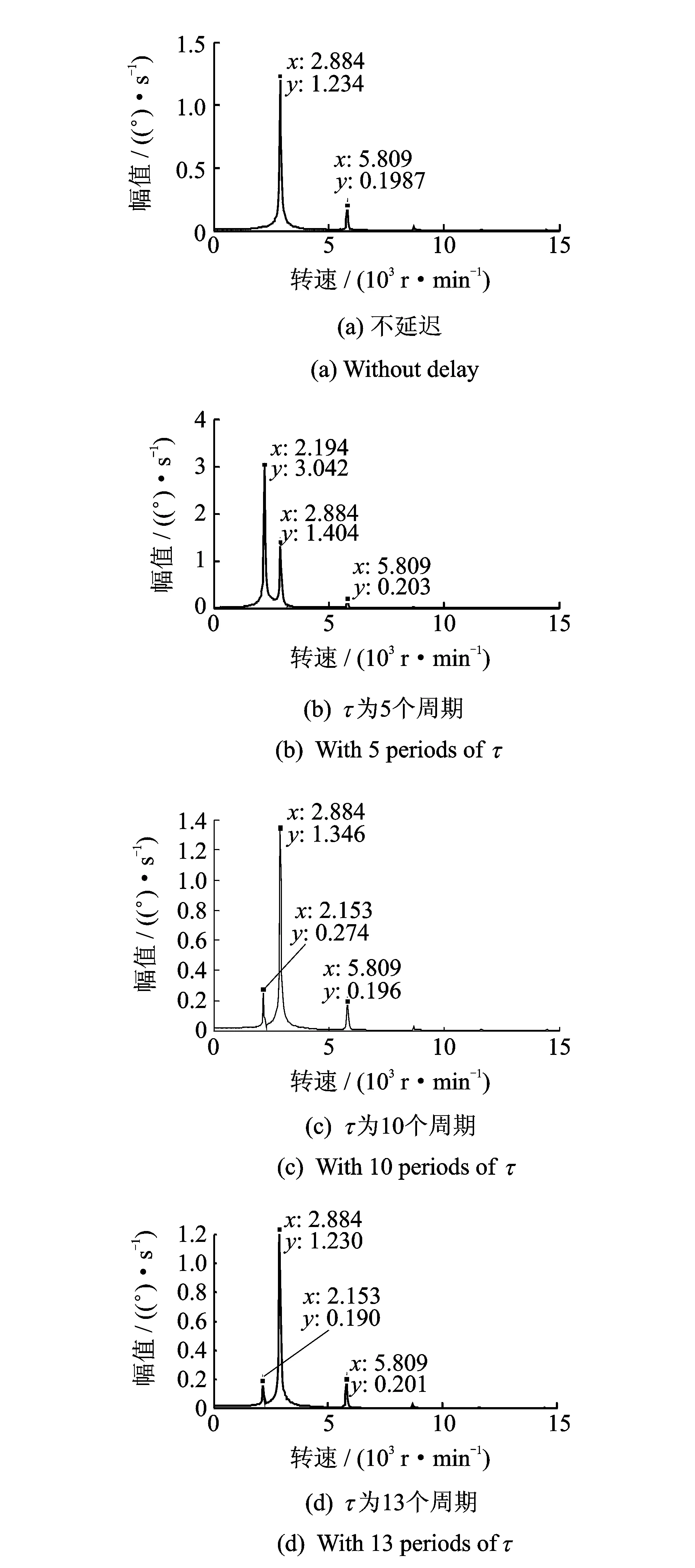
图11 1 300 r·min-1时不同控制力矩延迟下转子扭转振动频谱Fig.11 The frequency spectrum of torsional vibration with different control torque at 1 300 r·min-1

图11为1 300 r·min-1时不同的控制力矩延迟下转子扭转振动频谱。从图中可以看出，当控制力矩没有延迟时，扭振的频谱中没有扭振自振频率成分，这是由于当控制力矩没有延迟时，相当于对系统提供了一个扭振阻尼，于是系统的扭振自振频率成分迅速衰减。而当控制力矩有延迟时，如果延迟的时间恰好造成了对系统提供了扭振负阻尼，那么系统就会发生扭振失稳，扭振自振频率成分占优。而在延迟10个旋转周期以及13个旋转周期时，扭振频谱主要为正碰力冲击频率成分，同时也伴有扭振自振频率成分。

图12为控制力矩延迟为5个旋转周期以及12个旋转周期时的轴心轨迹。由图12可以看出，当控制力矩延迟为5个旋转周期时，随着扭振的失稳，转速的波动也影响了转子的横向振动，使得转子的轴心轨迹复杂，控制力矩延迟为13个旋转周期时的轴心轨迹则呈现规则的花瓣状。

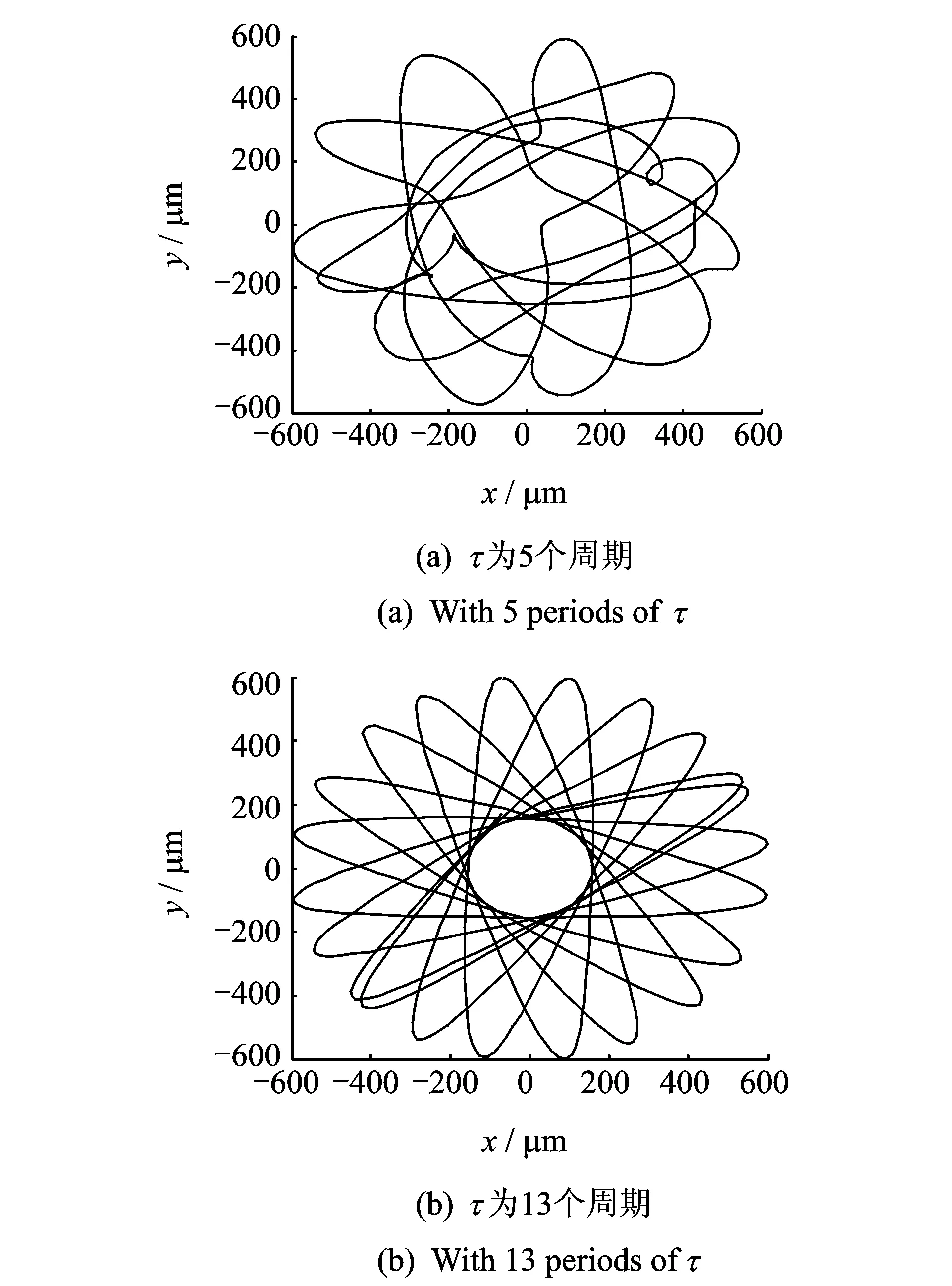
图12 1 300 r·min-1时不同控制力矩延迟下的轴心轨迹Fig.12 The axis orbit with different control torque at 1 300 r·min-1

综上所述，由于航空发动机的工作特点，其转速控制力矩的延迟是不可避免的。这有可能使得转/静子碰摩引起的转子扭转振动失稳,还应根据发动机控制系统的特性和控制律进行进一步的研究。

4 结论

1) 转子/机匣碰摩会引起转子弯扭耦合振动，剧烈的碰摩会导致转子反进动。

2) 转子/机匣碰摩的摩擦力矩会导致转子发生扭转振动，而对于航空发动机这类转速控制力矩存在延迟的转子系统，可能引起转子扭振失稳，导致弯扭耦合振动加剧。摩擦力矩越大，转子越易于发生扭振失稳。

3) 由于转速控制力矩延迟的存在，即使不出现扭振失稳，转子/机匣碰摩引起的转子扭转振动也会持续发生，且幅值较大。

4) 转子扭振信号可以作为转子/机匣发生碰摩的重要诊断信息之一。

[1] 马辉,太兴宇,李焕军，等.旋转叶片-机匣碰摩模型及试验研究综述[J].航空动力学报,2013, 28(9):2055-2069.

Ma Hui, Tai X Yingyu, Li Huanjun J, et al. Literature survey of rub-impact model and experiment of rotating blade and casing[J]. Journal of Aerospace Power, 2013, 28(9):2055-2069. (in Chinese)

[2] Issam Abu-Mahfouz, Amit Banerjee. On the investigation of nonlinear dynamics of a rotor with rub-impact using numerical analysis and evolutionary algorithms[J]. Procedia Computer Science, 2013(20):140-147.

[3] Varney P, Green I. Nonlinear phenomena, bifurcations, and routes to chaos in an asymmetrically supported rotor-stator contact system[J]. Journal of Sound and Vibration, 2015(336):207-226.

[4] Chávez J P, Hamaneh V V, Wiercigroch M. Modelling and experimental verification of an asymmetric Jeffcott rotor with radial clearance[J]. Journal of Sound and Vibration, 2015(334):86-97.

[5] 曹登庆,杨洋,王德友,等.基于滞回碰摩力模型的转子系统碰摩响应研究[J].航空发动机,2014, 40(1):1-9.

Cao Dengqing, Yang Yang, Wang Deyou, et al. Study on rub-impact responses of rotor systems based on hysteretic rub-impact force model[J]. Aeroengine, 2014, 40(1): 1-9. (in Chinese)

[6] Ma Hui, Zhao Qianbin, Zhao Xueyan, et al. Dynamic characteristics analysis of a rotor-stator system under different rubbing forms[J]. Applied Mathematical Modelling, 2015(39):2392-2408.

[7]太兴宇，马辉，谭祯,等.叶片-机匣系统碰摩振动响应分析[J].振动、测试与诊断，2014,34(2):280-287.

Tai Xingyu, Ma Hui, Tan Zhen, et al. Analysis of vibration response during blade-casing rub events[J]. Journal of Vibration, Measurement & Diagnosis, 2014,34(2):280-287. (in Chinese)

[8]刘杨，太兴宇，姚红良,等.双盘转子轴承系统不对中-碰摩耦合故障分析[J].振动、测试与诊断，2013,33(5):820-823.

Liu Yang, Tai Xingyu, Yao Hongliang, et al. Study on misalignment-rubbing coupling fault of dual-disk rotor-bearing system including the impact of motor coupling[J]. Journal of Vibration, Measurement & Diagnosis, 2013,33(5):820-823. (in Chinese)

[9] 王俨剀，王理，廖明夫,等.双转子发动机-机匣碰摩振动特征研究[J].机械科学与技术，2014,33(4):614-620.

Wang Yanka, Wang Li, Liao Mingfu, et al. Exploring vibration characteristics of dual-rotor engine’s rotor-to-case rub-impact[J]. Mechanical Science and Technology for Aerospace Engineering, 2014,33(4):614-620. (in Chinese)

[10]王四季，廖明夫，蒋云帆,等.对转双转子局部碰摩故障实验[J].推进技术，2013,34(1):31-36.

Wang Siji, Liao Mingfu, Jiang Yunfan, et al. Experimental study on local rub-impact fault of counter-rotating dual-rotor[J]. Journal of Propulsion Technology, 2013,34(1):31-36. (in Chinese)

[11]于明月,陈果,刘永泉,等.基于机匣应变信号的航空发动机转静碰摩部位识别[J].航空学报,2013, 34(6):1474-1484.

Yu Mingyue, Chen Guo, Liu Yongquan, et al. Aero-engine rotor-stator rubbing position identification based on casing strain signals[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(6):1474-1484. (in Chinese)

[12]Vlajic N, Liu X, Karki H, et al. Torsional Oscillations of a Rotor with Continuous Stator Contact[J]. International Journal of Mechanical Sciences, 2014, 83(6):65-75.

[13]Lahriri S, Weber H I, Santos I F, et al. Rotor-stator contact dynamics using a non-ideal drive—Theoretical

and experimental aspects[J]. Journal of Sound and Vibration, 2012(331):4518-4536.

[14]邓小文，廖明夫，Liebich R, et al. 碰摩转子的弯曲和扭转振动分析[J]. 航空动力学报, 2002,17(1):97-104.

Deng Xiaowen, Liao Mingfu, Liebich R, et al. Coupled bending and torsional vibrations due to rotor-to-stator contacts[J]. Journal of Aerospace Power, 2002,17(1):97-104. (in Chinese)

[15]邓小文，廖明夫，Liebich R, et al. 双盘转子碰摩的弯曲和扭转振动实验研究[J]. 航空动力学报,2002,17(2):205-211.

Deng Xiaowen, Liao Mingfu, Liebich R, et al. Experimental research of bending and torsional vibrations of a double disc rotor due to rotor-to-stator contacts[J]. Journal of Aerospace Power, 2002,17(2): 205-211. (in Chinese)

[16]邓小文.双盘转子碰摩的弯曲和扭转耦合振动研究[D].西安：西北工业大学，2001.