不确定性参数识别的模态区间逆响应面法

2016-11-23骆勇鹏黄方林鲁四平韩建平

振动、测试与诊断 2016年5期

关键词：固有频率个数不确定性

骆勇鹏，黄方林，鲁四平，韩建平

(1.中南大学土木工程学院长沙,410075) (2.兰州理工大学土木工程学院兰州,730050)

不确定性参数识别的模态区间逆响应面法

骆勇鹏1，黄方林1，鲁四平1，韩建平2

(1.中南大学土木工程学院长沙,410075) (2.兰州理工大学土木工程学院兰州,730050)

结合模态区间分析及响应面的相关理论，提出一种新的不确定性参数识别方法，即模态区间逆响应面法。首先，以有界区间数来量化结构参数的不确定性，通过合理的实验设计确定样本数据；然后，以响应为输入，设计参数为输出，采用逐步回归分析构造设计参数与结构响应的模态区间逆响应面模型，进而直接在模态区间逆响应面模型上进行模态区间运算,即可识别材料参数的变异性区间；最后，采用一组钢板模态实验来验证所提方法的可行性及可靠性。结果表明：所提方法可准确识别钢板材料参数的取值区间，有效地解决多重变量区间运算存在的区间过估计问题，识别过程避免区间迭代优化，具有较高的计算效率。

参数识别；模态区间分析；响应面；不确定性

引言

工程结构总是不同程度地存在各种各样的误差和不确定性，如构件几何容差、材料参数的固有随机特性、边界条件变异及测试误差等。通常这些误差和不确定性较小，但结合在一起就可能导致结构的动力特性产生较大的偏差或不可预知性，从而影响到结构的可靠性和安全性评判。因此，如何准确量化这些不确定性是至关重要的[1-2]。现有解决不确定性问题的常用方法有概率统计分析、模糊分析及区间分析。概率统计分析通常假设不确定性参数等为随机变量，且满足某种概率分布假设，通过构建一个反问题来求得结构参数的概率统计特征，如随机模型修正方法[3-4]。模糊分析是利用模糊数学理论来研究不确定性问题，主要用来解决工程分析中的模糊性信息问题[5]。不管是隶属度函数还是概率分布函数的确定都需要大量的样本信息。然而对于实际问题，其参数样本往往是有限的，无法对不确定性参数的概率分布进行假设[6]，限制了这些方法在实际工程中的应用。

实际工程中，虽然不确定量的统计信息难以获得，但却较容易确定其确定性的边界，因此用有界区间数来描述不确定量是一种方便且可行的方法。近些年采用区间分析(interval analysis，简称IA)常用于解决不确定性问题，如含不确定性参数的静动力分析[6]、有限元模型修正及确认[7]和机械故障诊断[8]等领域。

不确定性的来源可分为4类：测试不确定性、计算不确定性、模型不确定性及参数不确定性[1]。不同种类的不确定性问题应予以区别对待。笔者主要研究结构参数不确定性的量化问题。受条件限制，结构参数的真值往往难以直接测定，此时根据结构响应变化量反向量化参数的不确定性是解决该问题的一个好方法。笔者结合逆响应面及模态区间分析(modal interval analysis，简称MIA)的相关理论，提出一种基于模态区间逆响应面(modal interval inverse response surface，简称MIIRS)的不确定性参数识别方法。该方法避免了区间迭代优化过程且有效解决区间过估计问题，有效地提高计算效率和识别精度。最后，以一组钢板的不确定性材料参数识别为例，验证所提方法的可行性及可靠性。

1 MIA简介

MIA是将IA和模态逻辑相结合，利用模态谓词逻辑对区间进行语义学解释，从而进行符合模态逻辑语义解释的区间分析[9-10]。

以显式函数f(X)和g(X)为例，说明MIA方法在解决多重变量区间扩张问题上的优势。式(1)和(2)两个函数在数学上来说是一样，仅表达方式不同。现分别采用IA和MIA方法求解两个函数在参数空间x1=[1,2]，x2=[3,4]上的取值范围。已知函数的精确解为[19, 40]。

(1)

(2)

f(X)和g(X)的IA计算结果分别为[13，46]和[19, 40]。从计算结果可知，函数g(X)的计算结果与精确解一致，而函数f(X)的计算结果大于精确解，出现了区间扩张的问题。这是由于在函数中多次出现的变量存在相关性，且其单调性不一致所导致的。

采用MIA再次计算两个函数的取值区间。首先分别确定函数对多重事件x1和x2的单调性，接着根据强制最优理论，将单调趋势与其所对应的多重事件变量的单调趋势相反的独立子事件变量变成对偶形式，如式(3)和式(4)所示，最后直接进行模态区间运算。

(3)

(4)

f(X)和g(X)的MIA计算结果均为[19, 40]，与精确解一致。结果表明，MIA可以有效改善IA在处理多重事件时存在的区间扩张问题。

2 不确定性参数识别过程

笔者结合模态区间分析及逆响应面法[11]的相关理论，提出一种新的不确定性参数识别方法，即MIIRS法。该识别方法主要包括：实验设计、区间逆响应面建模、精度检验、MIIRS建模及模态区间运算5大部分，其流程如图1所示。由于模态区间运算已在第1节进行介绍，以下仅对前4部分进行论述。

图1 基于模态区间逆响应面的不确定性参数识别流程Fig.1 The flow chart of uncertain parameter identification based on MIIRS

2.1 实验设计

合理的实验设计关系到能否拟合到高精度的MIIRS。常用的实验设计方法有均匀设计、中心复合设计(central composite design，简称CCD)、D-最优化设计等。由于输入变量是不方便直接给定的结构响应，因此在MIIRS建模过程中采用与响应面法相同的实验设计方法来确定实验点，然后计算各试验点所对应的响应获得样本数据。然而值得注意的是，当设计参数较少，结构响应较多时，采用传统试验设计方法确定的实验点会少于MIIRS建模需识别的回归系数的个数，从而导致回归方程无法求解，此时需要增加设计点的个数。

本研究采用的实验设计方法为CCD，其设计点由2k析因设计添加2k个坐标轴点和nc个中心点所组成[12]。四输入二输出的二阶MIIRS所需识别的回归系数个数M及实验设计所确定的设计点个数N如表1所示。从表1中可知，CCD和D-最优设计分别至少需要增加6个和9个设计点。

表1 设计点及回归系数的个数

Tab.1 The number of design points and regression coefficient

方法设计点个数NCCDD-最优设计回归系数个数M计算公式2k+2k+nc12k+1()k+2()1+2m+mm-1()2样本数9615

2.2 区间逆响应面建模

在MIIRS建模前，需先拟合区间逆响应面模型。区间逆响应面与响应面类似，根据实际工程的复杂程度等因素可采用多项式、高斯过程模型、神经网络模型及幂函数等形式。式(5)为常用的完全二阶区间逆响应面的表达式。

(5)

为了节约后期MIIRS建模过程中，多重事件变量及其子变量单调性判断的计算成本，采用逐步回归分析方法[13]建立区间逆响应面模型。该方法在引入或剔除一个变量时均要进行F检验，以保证在引人新变量前回归方程中只含有对X影响显著的变量，而不显著的变量已被剔除。

2.3 精度检验

2.4 MIIRS建模及量化过程

为避免区间运算过程导致区间过估计的问题，引入MIA方法。在进行模态区间运算前，先采用强制最优理论对区间逆响应面模型进行“对偶”变换。

强制最优理论[8,10]为：设X为区间矢量，f R定义在X′上，并且对多重事件变量完全单调，设XD是X的扩展矢量，每个多重事件变量的子事件变量都作为XD中一个独立的子事件，如果任意独立子事件变量单调趋势与其所对应的多重事件变量的单调趋势相反，则需将此变量变成对偶形式，则有

(6)

经过以上步骤，可以得到改进后的区间逆响应面模型，即MIIRS。最后直接在MIIRS的表达式上进行模态区间运算，即可达到不确定性参数识别的目的。

3 实验验证

文献[15]在自由-自由边界条件下，采用锤击法对33块钢板进行模态实验，得到33块钢板的模态固有频率值，其固有频率实测值及统计特征值如表2所示。表中f1,…,f2分别表示第1阶，…，第5阶频率。该组钢板的名义尺寸为564mm×110mm×1.45mm，初始弹性模量E取值为210 GPa，剪切模量G取值为83 GPa，质量密度D为7 860 kg/m3。

表2 固有频率实测值及其统计特征值

Tab.2 The measured frequencies and its statistical features

在实际工程中，材料参数取值通常是采用给定的名义值，受测试误差、制造工艺及环境条件改变等因素的影响，该名义值与真值不可避免地存在一定的误差。假设固有频率的变异性是由钢材的材料参数E和G的不确定性引起的。由于钢材材料参数的变异性通常取5%[16]，参考相关文献钢板单轴拉伸实验结果，确定E和G的初始取值区间分别为[200，220]，[76，90]。根据模态实验得到的固有频率统计特征值，采用所提方法识别不确定材料参数的取值区间。

为研究不同输入参数对识别结果的影响，以固有频率为输入，E和G为输出，试验设计分成3种工况，如表3所示。分别采用逐步回归分析方法拟合3种工况下的区间逆响应面模型。限于篇幅，仅给出工况2的区间逆响应面模型表达式，如式(7)和(8)所示，式中f1I，f2I，f3I为区间变量，分别表示前3阶固有频率。两个区间逆响应面模型的精度检验值如表4所示。从表中可知，3个检验准则计算值基本上为1，表明所拟合的响应面模型精度很高，且预测能力很好，可以用于后续的区间估计。

表3 3种工况及实验点个数

表4 模型精度检验值(工况2)

Tab.4 The test values of interval RSM of case 2

E,GR2R2adjR2predE/GPa1.001.001.00G/GPa1.000.990.99

E(X)=16．372 88+15．551 98x1I-5．761 19x2I-

0．281 42x3I+0．123 65x1Ix2I+0．004 53x2Ix3I

(7)

(8)

在得到两个区间逆响应面模型后，根据强制最优理论进行“对偶”变换得到MIIRS。式(9)和式(10)给出了工况2的MIIRS。

(9)

(10)

其中：Dual为对偶运算。

由表2可知前4阶固有频率的取值区间，直接在MIIRS上进行模态区间运算，识别E和G的取值区间。表5给出3种工况下E和G的识别结果。为便于比较分析，随机模型修正的识别结果[15]也列于表5，其上界和下界的值是根据修正后的均值及方差计算其95%置信水平下的置信区间而得。由表5可知，3个工况识别得到材料参数中值均符合钢板材料特性，但是工况1识别的材料参数取值区间大于其他两个工况及随机模型修正的取值区间。从图2～图4可知，工况3预测的固有频率的离散性最小，最接近于实测固有频率统计值；工况1预测的固有频率的离散性最大。因此可得工况3材料参数的取值区间最接近于钢板材料参数的实际取值区间。3个工况对比结果可知，输入个数对识别结果有一定的影响，输入个数越多，识别精度越高。但是输入个数越多，判别多重事件变量的单调性及确定试验点的计算成本越高，因此建议输入个数不宜少于输出个数，可取比输出个数多1～2个，以避免信息欠定而造成识别精度降低。

表5 不同工况的材料参数识别结果

Tab.5 The identified results of the plate material properties based on different case

工况工况1工况2工况3文献[15]E/GPa[200.96,215.43][201.39,213.72][202.19,213.65][204.50,214.69]G/GPa[80.53,92.61][82.23,88.39][82.21,88.41][80.86,86.74]

图2 工况1初始、实测及预测的前3阶固有频率散点图Fig.2 Initial, measured and predicted scatter plot of first three frequencies in case one

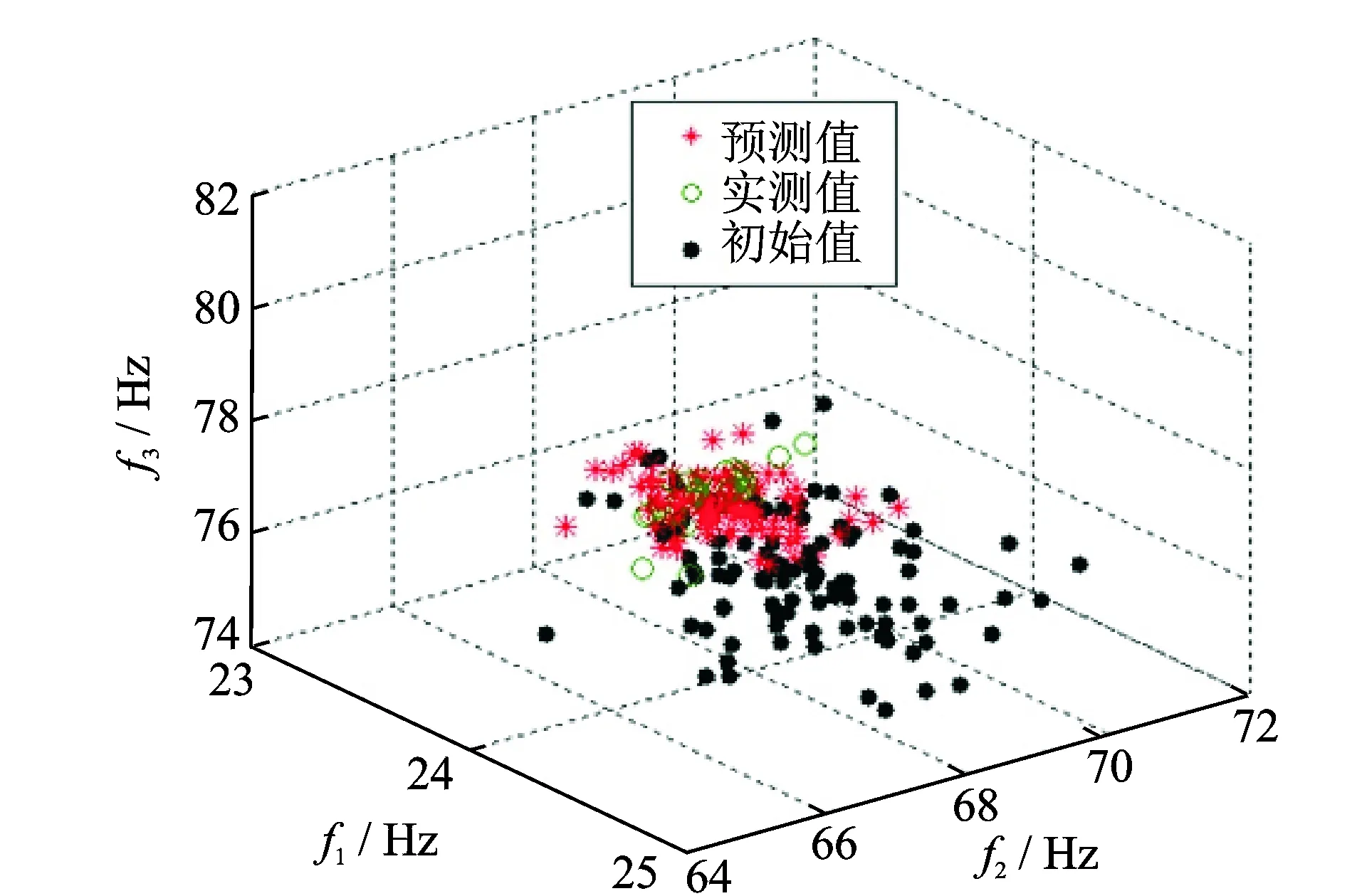
图3 工况2初始、实测及预测的前3阶固有频率散点图Fig.3 Initial, measured and predicted scatter plot of first three frequencies in case two

图4 工况3初始、实测及预测的前3阶固有频率散点图Fig.4 Initial, measured and predicted scatter plot of first three frequencies in case three

与随机模型修正方法相比，所提方法仅需在计算构造MIIRS所需的样本数据时进行少数的有限元计算，后续整个不确定性识别过程均不再涉及有限元模型，识别过程不需要迭代优化过程。相较于随机模型修正方法，为获得足够的样本数据而采取上千次的有限元计算，所提方法不仅能够保证计算精度，且大大地降低了计算花费，显著提高了不确定性参数的识别效率。

4 结论

1) 模态区间分析方法可有效解决传统区间运算导致的区间过估计问题，所提方法准确地识别出钢板材料参数的变异性区间，具有较高的识别精度。

2) 在模态区间逆响应面模型的表达式上直接进行模态区间运算，避免迭代优化过程，显著提高了计算效率。

3) 输入(实测固有频率)个数对识别结果有一定的影响，输入个数越多，识别精度越高。同时，输入个数越多，判别多重事件单调性及实验点确定的计算成本越高，建议输入个数不少于输出个数，以避免信息欠定造成识别精度降低。

[1] 万华平. 结构动力不确定性及其随机模型修正方法研究[D]. 长沙:中南大学, 2014.

[2] Steenackers G, Guillaume P. Finite element model updating taking into account the uncertainty on the modal parameters estimates [J]. Journal of Sound and Vibration, 2006, 296(4-5):919-934.

[3] Mares C, Mottershead J E, Friswell M I. Stochastic model updating: Part1—theory and simulated example [J]. Mechanical Systems and Signal Processing, 2006, 20(7):1674-1695.

[4] 方圣恩, 林友勤, 夏樟华.考虑结构参数不确定性的随机模型修正方法[J]. 振动、测试与诊断, 2014, 34(5):832-837.

Fang Shengen, Lin Youqin, Xia Zhanghua. Stochastic model updating method considering the uncertainties of structural parameters [J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(5) : 832-837.(in Chinese)

[5] 苏静波，邵国建.基于区间分析的工程结构不确定性研究现状与展望[J].力学进展, 2005, 35(3): 338 -344.

Su Jingbo, Shao Guojian. Current research and prospects on interval analysis in engineering structure uncertainty analysis[J].Advance in Mechanics, 2005, 35(3):338-344.(in Chinese)

[6] 邱志平.非概率集合理论凸方法及其应用[M].北京:国防工业出版社, 2005:3-10.

[7] 何成, 陈国平, 何欢.径向基模型的不确定性模型区间修正与确认[J].机械工程学报, 2013, 49 (11) :128-134.

He Cheng, Chen Guoping, He Huan. Interval model updating and validation with uncertainty based on the radial basis function[J]. Journal of Mechanical Engineering, 2013, 49(11): 128-134. (in Chinese)

[8] 樊久铭, 王秋生, 徐敏强，等.基于模态区间分析的半定性故障诊断方法[J].哈尔滨工业大学学报, 2007, 39(5):774-778.

Fan Jiuming, Wang Qiusheng, Xu Minqiang, et al. Semi-qualitative fault diagnosis method based on modal interval analysis [J].Journal of Harbin Institute of Technology, 2007, 39(5):774-778.(in Chinese)

[9] Ernest G, Sainz M, Lambert J, et al. Modal intervals [J].Reliable Computing, 2001, 7(2):77-111.

[10]Sainz M A, Armengol J, Remei Calm, et al. Modal interval analysis[M]. Switzerland: Springer International Publishing, 2014:17-140.

[11]张伟杰, 陆秋海, 缑百勇, 等.基于逆响应面法的有限元模型修正[J].噪声与振动控制,2013,33(6): 5-10.

Zhang Weijie, Lu Qiuhai, Gou Baiyong, et al. An inverse response surface method for finite element model updating [J]. Noise and Vibration Control, 2013, 33(6): 5-10.(in Chinese)

[12]韩建平, 骆勇鹏, 郑佩娟，等. 基于响应面的刚构-连续组合梁桥有限元模型修正[J].工程力学, 2013, 30(12):85-90.

Han Jianping, Luo Yongpeng, Zheng Peijuan, et al. Finite element modal updating for a rigid frame-continuous bridge base on response surface method [J]. Engineering Mechanics, 2013, 30(12)：85-90.(in Chinese)

[13]周纪芗. 实用回归分析方法[M].上海：上海科学技术出版社, 1990:102-112.

[14]Montgomery D C. Design and analysis of experiments [M]. New York: Wiley, 2003:484-488.

[15]Abu H N, Haddad K H, Huajiang O. Parameter selections for stochastic uncertainty in dynamic models of simple and complicated structures[C]∥Proceedings of the 10th International Conference on Recent Advances In Structural Dynamics. UK：University of Southampton，2010.

[16]李国强, 黄宏伟，吴迅，等. 工程结构荷载与可靠度设计原理[M]. 2版.北京:中国建筑工业出版社, 2001:126-128.