基于Kane方法的波浪驱动水下航行器动力学模型建立

杜晓旭，崔航，向祯晖

（1.西北工业大学航海学院，陕西西安710072；2.昆明船舶设备集团有限公司，云南昆明650051）

基于Kane方法的波浪驱动水下航行器动力学模型建立

杜晓旭1，崔航1，向祯晖2

（1.西北工业大学航海学院，陕西西安710072；2.昆明船舶设备集团有限公司，云南昆明650051）

基于多体系统动力学理论，定义并选取适当的坐标系和广义坐标，对波浪驱动水下航行器多体系统进行运动学分析，得到各部分的速度和加速度；基于Kane方法进行动力学分析，计算各部分的偏速度和偏角速度，进而求得系统的广义主动力和广义惯性力。将系统的广义惯性力和广义主动力代入Kane方程中，得到波浪驱动水下航行器多体系统动力学模型。在受力分析中，不仅考虑了惯性力、惯性力矩、重力和浮力以及流体动力，还重点分析了波浪力和多体系统的附加质量力。对波浪驱动水下航行器进行了运动仿真，仿真结果显示航行器航行稳定，所建立的模型是有效的。

兵器科学与技术；Kane方程；波浪驱动水下航行器；多体系统动力学

0 引言

如今，海洋能源的利用和开发已成为一种新的趋势，这无疑对海洋的监测开发平台提出了新的要求。Hine等［1］从2005年开始研制波浪动力滑翔机，并很快制造出第一代样机；美国Liquid Robotics公司研制了两种SV系列的波浪动力滑翔机，可进行长时间、大范围的自主航行，并不需要电力驱动，仅通过转化波浪能得到航行的动力，同时可搭载各种传感器，获取海洋近水面的各种参数。

对于上述波浪动力滑翔机的建模方法，国外主要采用拉格朗日方法。Caiti等［2］通过计算动能，势能以及瑞利耗散函数，代入拉格朗日方程得到动力学模型；李小涛［3］应用有限元方法和刚体动力学方法建立水面航行的波浪驱动滑翔机的动力学模型。Yang等［4］应用Kane方法建立了水下蛇形机器人的动力学模型，他们计算偏速度，推导广义主动力和广义惯性力的表达式，得到其动力学方程；Mohan等［5］通过应用Kane方法建立带机械臂水下航行器的动力学模型，他们进行了详细的推导；贾丽娟［6］应用Kane方法建立了水面航行的波浪动力滑翔机的动力学方程，仿真结果显示能实现稳定航行。而目前对于既要考虑波浪力也要考虑附加质量力的多体系统动力学建模的研究还较少。

波浪驱动水下航行器主要由近水面航行器、连接缆索和多翼扑动驱动体三部分组成，运动方式如下:近水面航行器在波浪作用下上下波动，通过缆索带动驱动体起伏运动，从而使翼板摆动产生推力，反过来带动航行器向前运动。与水面航行的波浪动力滑翔机相比，波浪驱动水下航行器的主要特点在于其隐蔽性，与水面浮体相比，水下航行器的隐蔽性更高，不易被发现，这对作战侦查是非常有意义的。并且在建模过程中，对于波浪动力滑翔机可认为水面浮体的运动幅度近似等于波浪自由表面的运动幅度，其运动学方程就不必再求解，只需要研究水下驱动体和缆索的运动，属于弱耦合的情况，而本文研究对象完全在水下运动，整个系统的运动都是未知的，运动方程都需要求解，属于强耦合的情况，这给动力学建模的仿真带来了难度。

本文的研究目的是根据动力学模型对波浪驱动水下航行器在不同缆索长度和不同航行深度下的运动情况进行研究。为了实现波浪驱动水下航行器的运动，在垂向水下航行器必须满足一定的运动幅度，不同的航行深度和缆索长度会导致航行器在垂向运动幅度的不同，从而影响水下驱动体多翼扑动产生的推力，使得航行速度随之改变；从能量方面来说，波浪驱动水下航行器主要是利用波浪能，将其转化为前进的动力，而波浪能与航行深度和缆索长度密切相关，因此航行速度会随之改变。

本文基于多体系统研究方法，定义恰当的坐标系，对波浪驱动水下航行器进行运动学分析，得到位置、速度等表达式，通过Kane方法，对波浪驱动水下航行器进行动力学分析，通过分析受力，计算得到广义惯性力和广义主动力，最后将计算结果代入Kane方程中，得到波浪驱动水下航行器的动力学方程，仿真结果显示水下航行器航行稳定。

为了简化波浪驱动水下航行器的动力学模型，本文仅研究其在纵平面的运动，并作如下假设:

1）实际的波浪驱动航行器采用的是圆形截面的弹性缆索，会发生弹性形变，进而造成水下驱动体运动的相位滞后现象，导致波浪能的损失，但由于本文研究对象的连接缆索长度较短，并且整个系统的运动速度并不快，故该缆索的弹性变形很小。同时从其运动机理可以看出，缆索一直处于张紧的状态，所以在误差允许的范围内，本文在建模时假设缆索为刚性缆索，不会发生弹性形变；

2）由于本文对整个系统在纵平面运动进行建模，故在航行过程中，各部分的质心和浮心应处于同一垂直平面；

3）忽略波浪对缆索上端的影响。

1 坐标系与转换矩阵

为了将波浪驱动水下航行器多体系统的三部分联系起来，故选择如下坐标系［7-8］分析波浪驱动水下航行器的运动，如图1所示。

如图1所示，建立4种坐标系，分别为:Osxsyszs表示原点位于无波浪的海平面上的系统坐标系，为空间固定的笛卡尔坐标系，所有的运动学和动力学方程均以系统坐标系为基准，所有的计算也转换到系统坐标系下进行；Ovxvyvzv表示以浮心为原点的航行器体坐标系；Ocbtn表示以质心为原点的缆索局部坐标系；Odxdydzd表示以浮心为原点的驱动体的体坐标系。图1中的符号有以下定义:

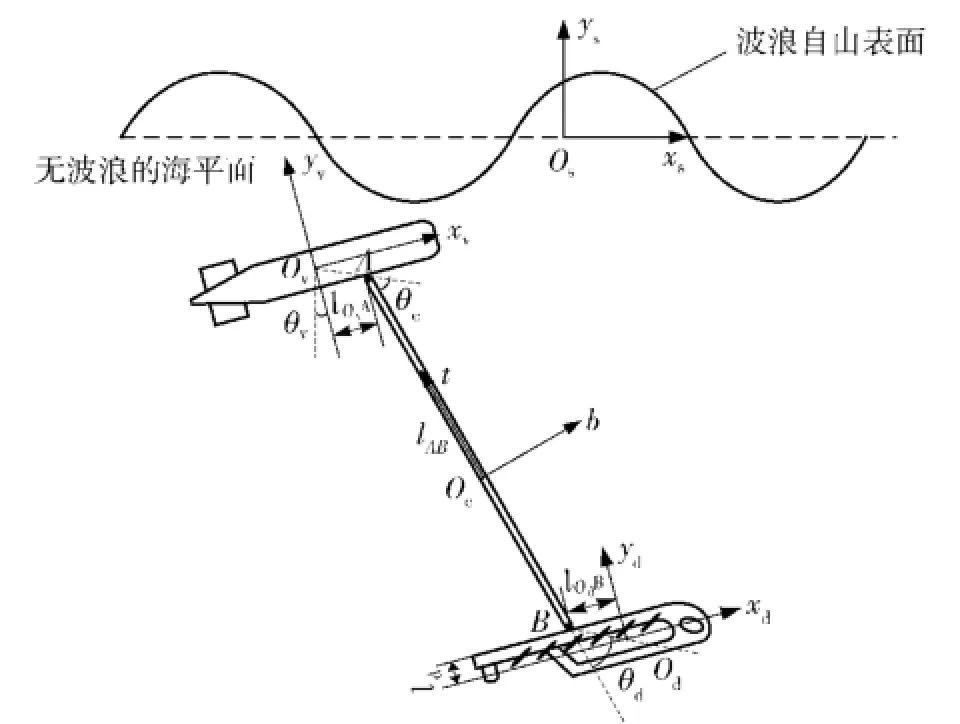
图1 波浪驱动水下航行器的坐标系Fig.1 Coordinate system of wave-driven underwater vehicle

θv:近水面航行器的俯仰角；

θc:缆索相对于水下航行器的摆角；

θd:驱动体相对于缆索的摆角；

D:航行器的直径；

A:绳索与航行器的连接点；B:驱动体与绳索的连接点；

lOvA:缆索与水下航行器的连接点到航行器浮心在航行器体坐标系下的纵向距离；

lAB:缆索的长度；

lOdB:缆索与驱动体的连接点到驱动体浮心在驱动体的体坐标系下的纵向距离；

ld:缆索与驱动体连接点到驱动体浮心在驱动体的体坐标系下的垂向距离。

为了便于描述水下航行器、缆索和驱动体的位置与姿态，基于图1中的几何关系，定义并计算如下物理量:

为了得到航行器体坐标系，缆索局部坐标系和驱动体的体坐标系分别与系统坐标系之间的转化矩阵，定义如下角度:

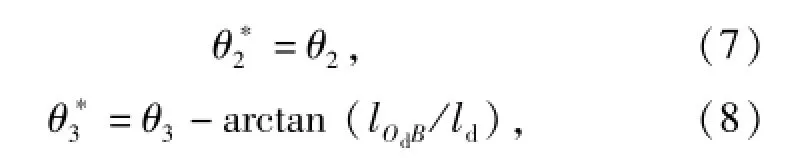
得到上述定义的角度后，可得转换矩阵为

2 运动学模型建立

本文运用多体系统研究方法［5，9］，并基于Kane方程建立波浪驱动水下航行器的运动学模型，选择如下广义坐标描述系统的姿态:

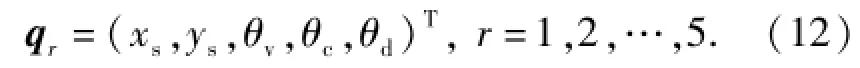
由上述广义坐标，可以得到波浪驱动水下航行器系统的广义速率为

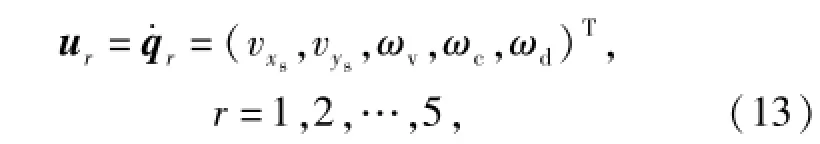
式中:vxs、vys分别为航行器浮心的速度在系统坐标系xs轴和ys轴的分量；ωv，ωc，ωd分别为水下航行器，缆索和驱动体的旋转角速度。

由图1可得到航行器浮心Ov，缆索质心Oc和驱动体浮心Od在系统坐标系下的位置坐标，具体为

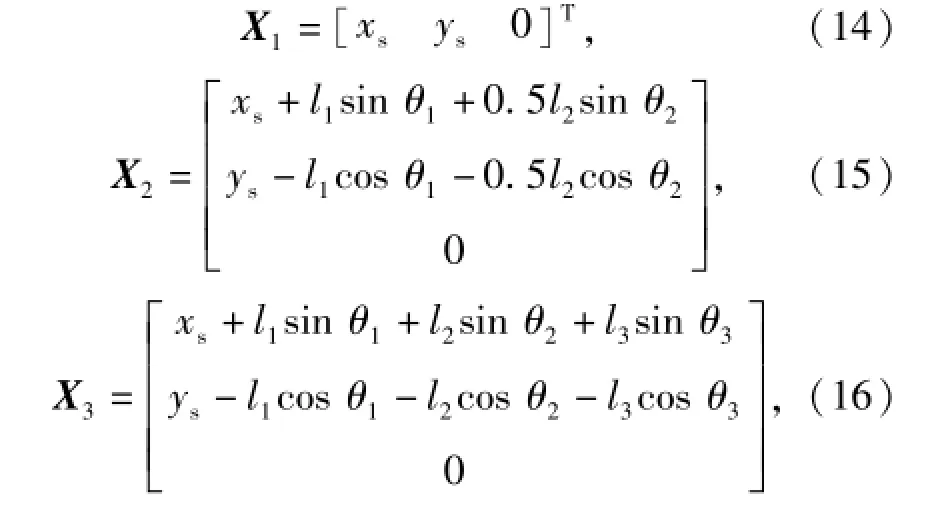
式中:X1、X2、X3分别为系统坐标系下航行器浮心Ov、缆索质心Oc和驱动体浮心Od的位置坐标。

对（14）式～（16）式求导，可得系统坐标系下的速度，具体为

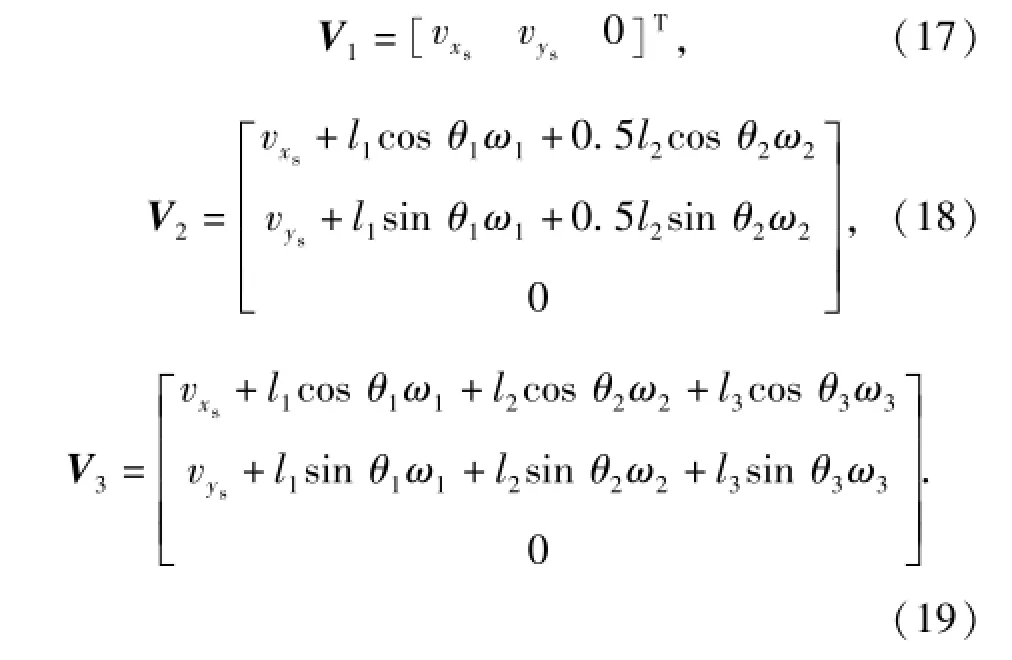
根据角速度的定义，可得到

式中:V1、V2、V3分别为系统坐标系下航行器浮心Ov、缆索质心Oc和驱动体浮心Od的速度；ω1、ω2、ω3分别为系统坐标系下航行器浮心Ov、缆索质心Oc和驱动体浮心Od的角速度。

同样地，对（17）式～（22）式求导，可得系统坐标系下的加速度和角加速度，具体为

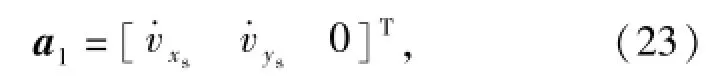
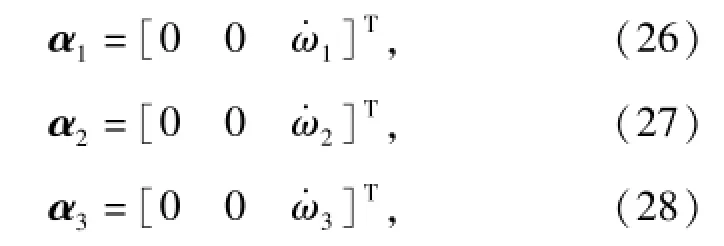
式中:a1、a2、a3分别为系统坐标系下航行器浮心Ov、缆索质心Oc和驱动体浮心Od的加速度；α1、α2、α3分别为系统坐标系下航行器浮心Ov、缆索质心Oc和驱动体浮心Od的角加速度。

根据偏速度和偏角速度的定义，（23）式～（28）式分别对广义速率ur求偏导，计算得到波浪驱动水下航行器各部分的偏速度和偏角速度为

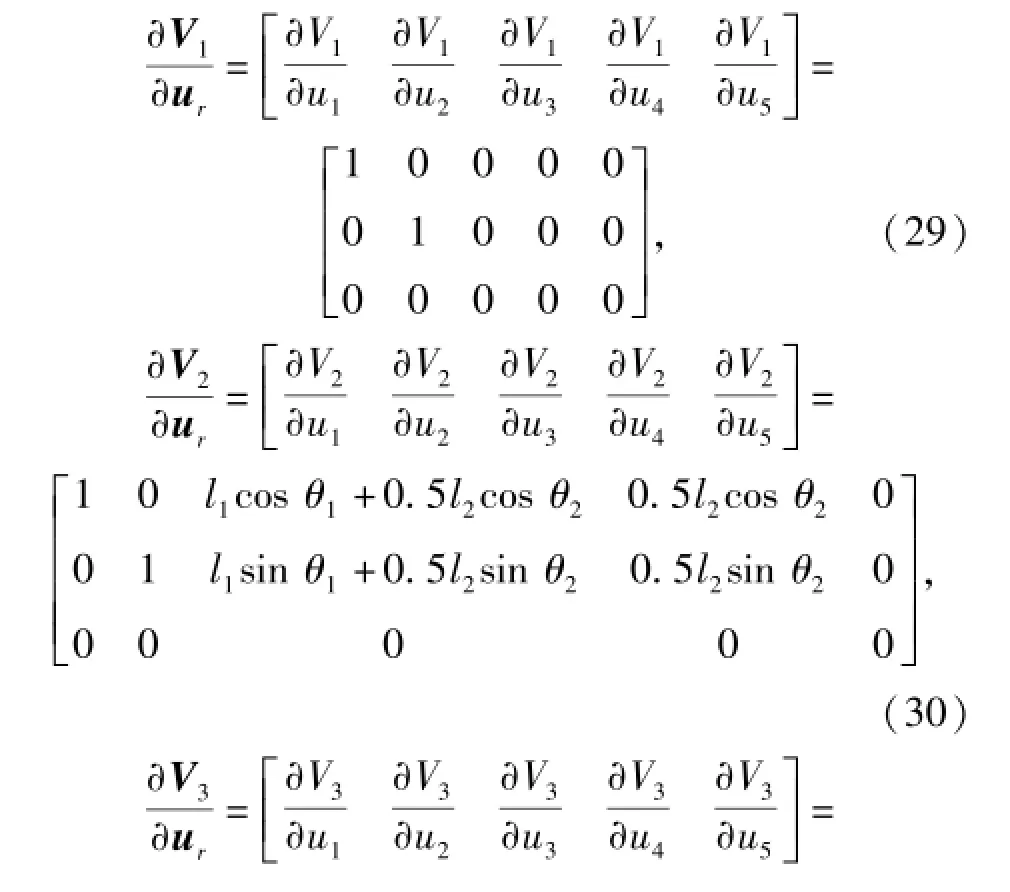
3 动力学模型建立

本节计算波浪驱动水下航行器的广义惯性力和广义主动力的表达式，代入Kane方程［9-11］中得到波浪驱动水下航行器多体系统动力学模型。

分别计算多体系统各部分在各自坐标系下受到的力，再通过转化矩阵得到在系统坐标系下受到的力的表达式，最后根据广义主动力和广义惯性力的定义，分别与各自的偏速度和偏角速度相乘，得到波浪驱动水下航行器系统的广义主动力和广义惯性力。

由广义主动力的定义，各部分的广义主动力可表示为

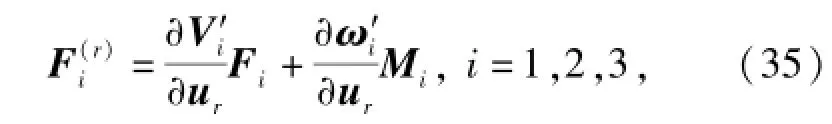
式中:i=1，2，3分别表示波浪驱动水下航行器系统的第1、2、3部分，具体指水下航行器、连接缆索和驱动体；Fi、Mi分别为第i部分受到的外力和外力矩；分别表示对的转置。

水下航行器在近水面运动时受到的外力主要有:重力、浮力、流体黏性位置力、流体黏性阻尼力、波浪力和附加质量力［7-8］。由于附加质量力具有质量的性质，故将附加质量力计入广义惯性力中（缆索和驱动体对附加质量力的处理方式相同）。除附加质量力外，水下航行器所受到的外力在航行器体坐标系下可表示为

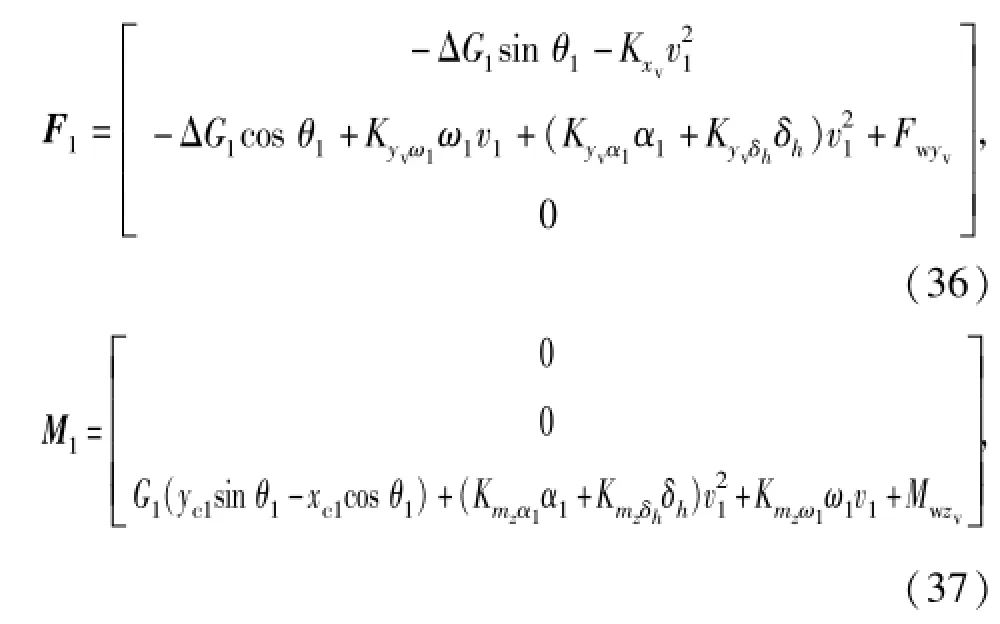
式中:ΔG1=G1-B1为航行器的负浮力，G1、B1分别为航行器的重力和浮力；xc1、yc1为航行器的重心到浮心的方向矢量在航行器体坐标系上的投影；Kxv、Kyvα1、Kyvδh、Kmzα1、Kmzδh分别为位置力及力矩的有量纲系数；Kyvω1、Kmzω1分别为阻尼力及力矩的有量纲系数；v1为航行器速度的大小；Fwyv、Mwzv分别为波浪对航行器的力和力矩。

对于航行器在近水面运动时受到的波浪力和力矩，本文采用切片法［12］计算。

水下缆索在运动过程中受到的外力主要有:重力、浮力、流体阻力和附加质量力。近似认为缆索的重力和浮力大小相等、方向相反、相互抵消；所选择的缆索为圆形截面缆索，故可认为缆索的浮心和重心重合，即重力和浮力在缆索质心处不会产生力矩。同时将缆索受到的流体阻力分为切向分力和法向分力来计算，并假定缆索的流体阻力作用点在缆索的质心处，故流体阻力不产生力矩。

基于上述分析和假设，缆索所受到的外力在缆索局部坐标系下可表示为

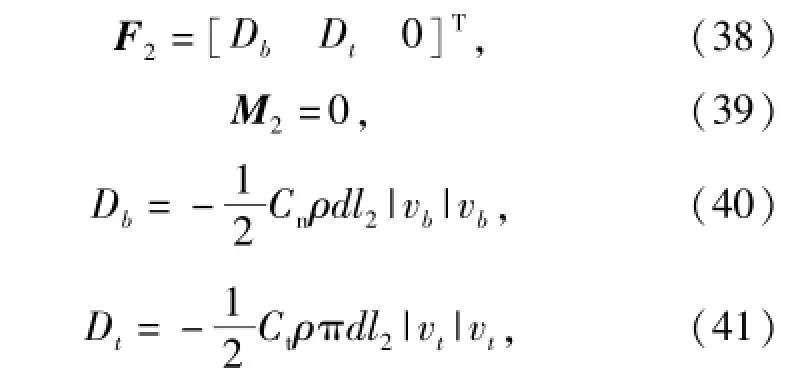
式中:Cn、Ct分别为缆索法向和切向阻力系数；ρ为海水密度；d为缆索直径；vb、vt分别为缆索浮心速度在缆索局部坐标系下的分量，可通过如下转化关系得到

驱动体在水下运动时受到的外力主要有:重力、浮力、流体黏性位置力、流体黏性阻尼力、附加质量力和多翼板扑动产生的推力。

除了附加质量力外，在驱动体的体坐标系下，驱动体所受到的外力可表示为

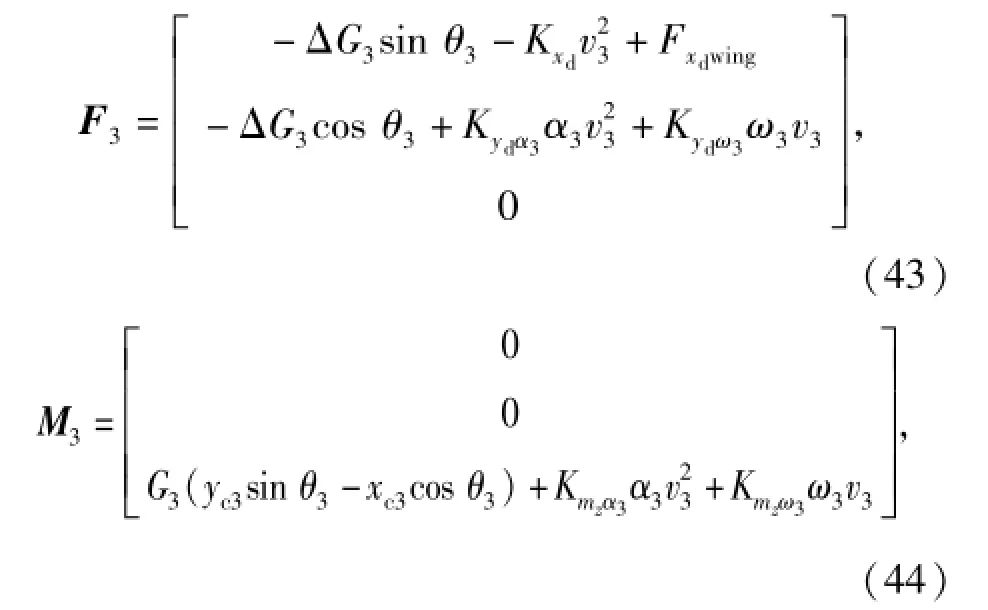
式中:ΔG3=G3-B3为驱动体的负浮力，G3、B3分别为驱动体重力和浮力；xc3、yc3为驱动体质心到浮心的方向矢量在驱动体的体坐标系上的投影；Kxd、Kydα3、Kmzα3分别为驱动体位置力及力矩的有量纲系数；Kydω3、Kmzω3分别为驱动体阻尼力及力矩的有量纲系数；v3为驱动体速度的大小；Fxdwing为翼板扑动产生的推力。

对于驱动体多翼扑动所产生的推力，可通过计算流体力学软件［13-14］计算得到。计算过程如下:将多翼模型导入ICEM中，在ICEM软件中建立多翼板计算域，并划分二维的非结构化三角形网格，在模型的近壁面处对网格进行加密，网格划分情况如图2所示。

图2 计算流域网格划分Fig.2 Grid partition of calculation domain

将处理好的文件导入FLUENT中，对初始条件进行设置，并设置监视器，利用动网格技术，实现对推力系数的数值模拟计算，得到不同频率、不同拍水幅度和不同来流速度下的推力值，最后在仿真时通过样条插值的方法对多翼扑动的推力进行计算。这里仅列举一种算例进行说明，在频率为0.5 Hz，拍水幅度为0.3c（c是翼板弦长），来流速度为0.1 m/s下，推力计算结果如图3所示。

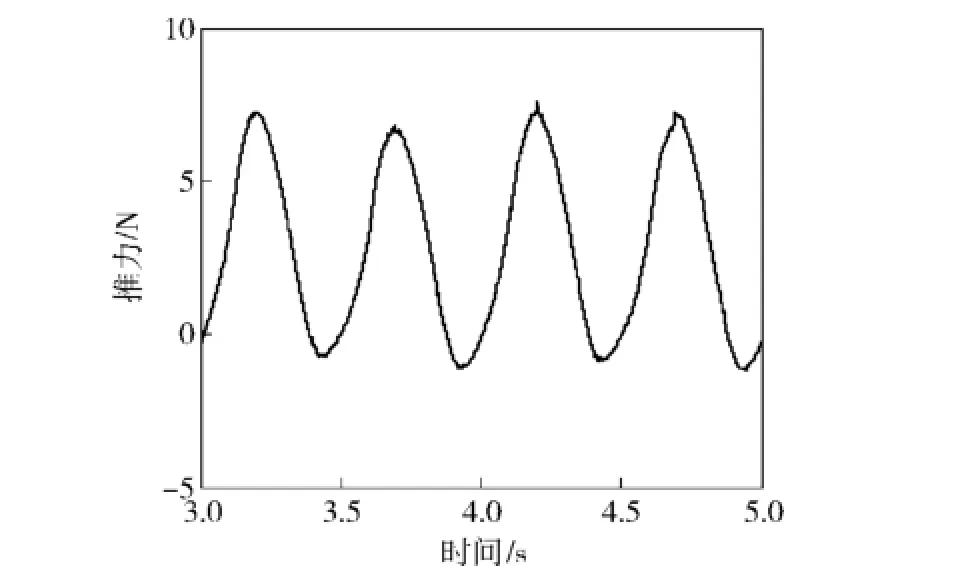
图3 推力随时间的变化Fig.3 Thrust vs.time

根据图3推力的变化规律，采用正弦形式的推力表达式近似驱动体多翼扑动的推力，具体表示为

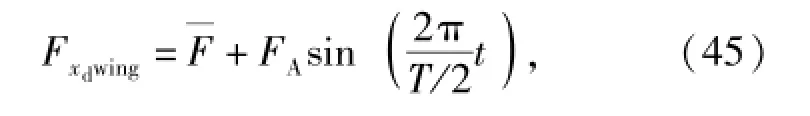
基于各部分的受力分析，将（36）式和（37）式、（38）式和（39）式、（43）式和（44）式分别代入（35）式得到各部分的广义主动力，最终波浪驱动水下航行器多体系统的广义主动力为

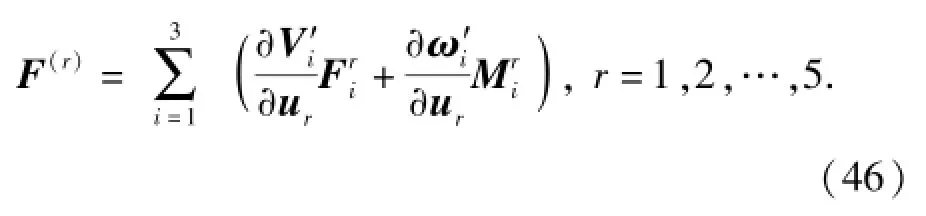
由于波浪驱动水下航行器在水下运动时会产生附加质量，在计算系统的广义惯性力时，不仅要考虑惯性质量，也要考虑附加质量的影响。

根据广义惯性力的定义，得到波浪驱动水下航行器各部分的广义惯性力为

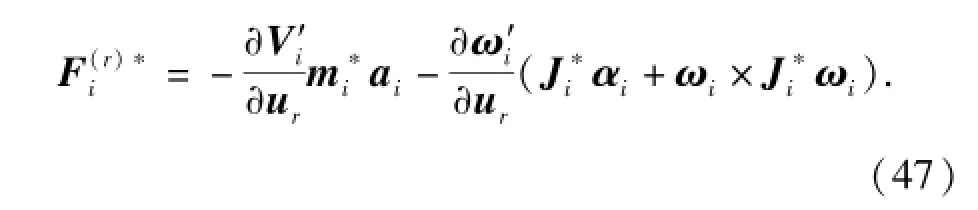
由于本文仅研究波浪驱动水下航行器在纵平面的运动，故（47）式中

则（47）式可化简为

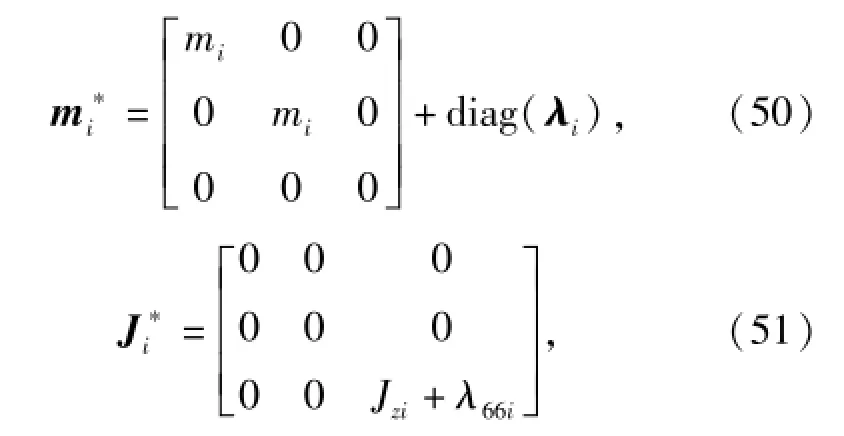
mi为第i部分的惯性质量，Jzi为第i部分的转动惯量，λ11i、λ22i、λ66i分别为第i部分的附加质量，λi为第i部分的附加质量在系统坐标系下的表达式，可通过下式计算得到:λi=［AOsOi］［λ11iλ22i0］T，其中Oi可取Ov、Oc和Od.

对于缆索这种细长圆柱体在水中运动时的附加质量，采用匡建平等［15］的研究方法计算，得到缆索的附加质量。具体计算方法为

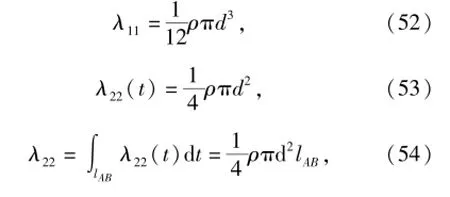
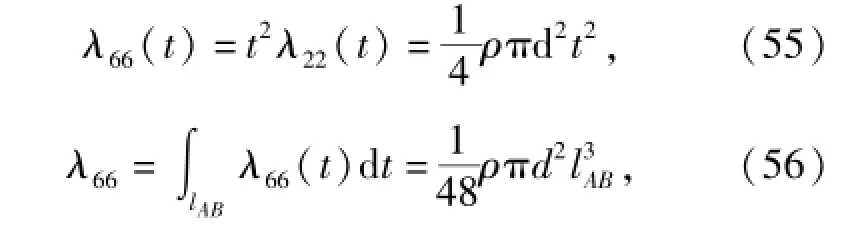
式中:t为缆索微元段距缆索质心的距离。由上述计算得到的各部分广义惯性力，可得到波浪驱动水下航行器系统的广义惯性力为

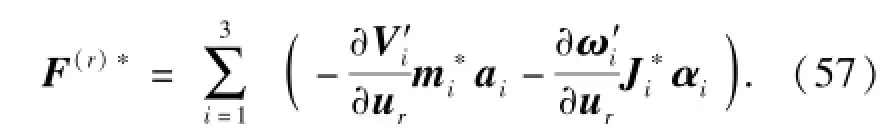
基于多体系统动力学理论，根据Kane方法建立的动力学模型为

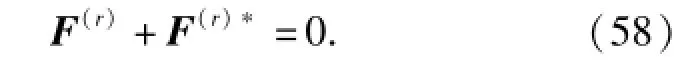
为了简化计算，忽略（46）式和（57）式中的高阶状态变量，并代入（58）式中，可得到波浪驱动水下航行器的多体系统动力学方程为

式中:

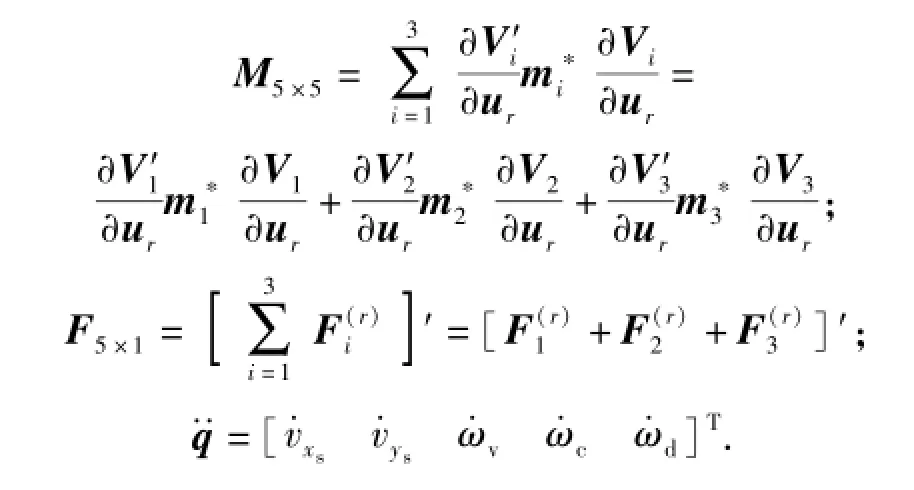
4 仿真

本文基于Kane方法建立的动力学模型，采用4阶龙格-库塔数值积分算法编制仿真程序，进行波浪驱动水下航行器的运动仿真研究。仿真参数如表1所示。

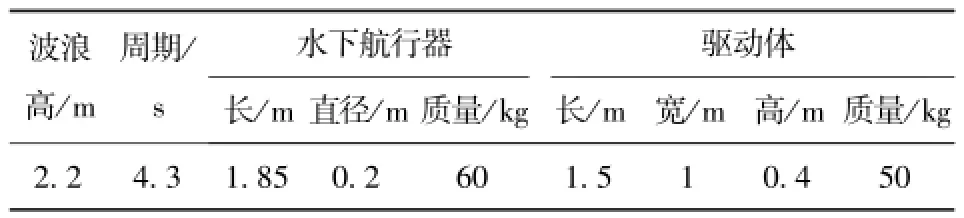
表1 仿真参数表Tab.1 Simulation parameters

在4级海况下，水下航行器的航行深度设定为5 m，仿真研究在不同缆索长度（3 m、4 m、5 m和6 m）下，波浪驱动水下航行器的运动特性，仿真结果如图4～图6所示。

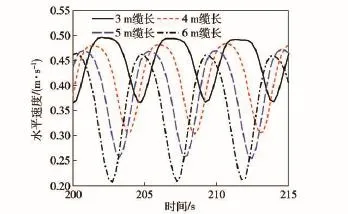
图4 不同缆索长度下航行器的水平速度图Fig.4 Horizontal velocities of underwater vehicles with different lengths of cable

图5 不同缆索长度下的运动轨迹图（上方为航行器的运动轨迹，下方为驱动体的运动轨迹）Fig.5 Motion tracks of underwater vehicles with different lengths of cable（upper:motion tracks of vehicles；below:motion tracks of drivers）

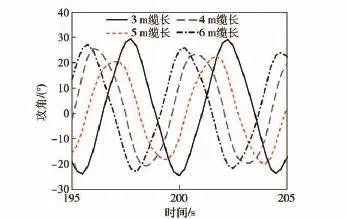
图6 不同缆索长度下驱动体的攻角图Fig.6 Attack angles of drivers with different lengths of cable

由图4和图5可得:在4级海况下，5 m航行深度时，选择不同缆索长度（3 m、4 m、5 m和6 m），波浪驱动水下航行器均能实现持续稳定航行，同时均能保持定深状态；航行器和驱动体在运动稳定后做周期性运动；缆索长度的不同会导致航行器的航行速度有所区别，对比分析可得，随着缆索长度的减小，航行器的速度有所提高，这是由于随着缆索长度的减小，对波浪能的损失会有所降低，故航行器的速度有所提高；缆索长度为3 m时的航行器速度相对较快，平均速度在0.42 m/s.但由于缆索长度的减小，驱动体也将受到波浪的影响，这不利于航行的稳定。同时由图6可以看出，在缆索长度为3 m时，驱动体攻角的变化幅度较大，这会影响驱动体运动稳定性和使用期限，故本文缆索长度选择为4 m.

在缆索长度为4 m的情况下，仿真研究4级海况下不同航行深度（4 m、5 m和6 m）时，水下航行器的运动特性，仿真结果如图7、图8所示。

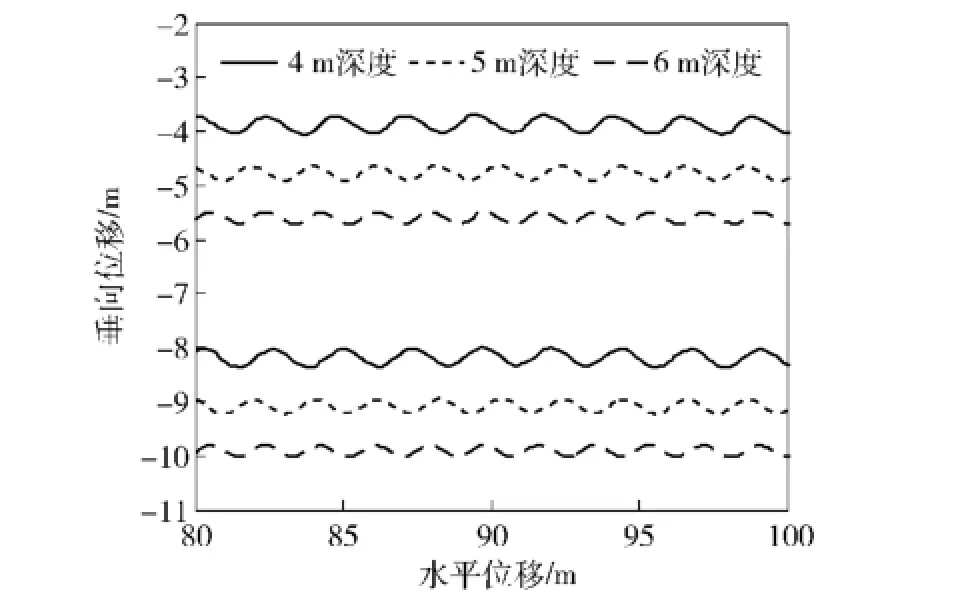
图8 不同深度下的运动轨迹图（上方为航行器的运动轨迹，下方为驱动体的运动轨迹）Fig.8 Motion tracks of underwater vehicle in different depths（upper:motion tracks of vehicles；below: motion tracks of drivers）

由图7和图8可得:波浪驱动水下航行器在4 m、5 m和6 m深度下，均能实现持续稳定航行，同时均能保持定深状态；航行器的航行速度与航行深度有关，随着深度的减小，航行器速度有所增加，这是由于随水下航行器航行深度的减小，整个系统所获得的波浪能有所增加，其前进的动力就会增加，因此，航行器的速度有所提高；在4 m深度时航行器的速度相对较大，平均速度在0.47 m/s左右。

5 结论

本文基于多体系统理论，采用Kane方法建立波浪驱动水下航行器的动力学模型。选择适当的坐标系和广义坐标，在忽略了波浪对驱动体和缆索的影响下，基于Kane方法，对波浪驱动水下航行器多体系统进行运动学分析，得到速度和加速度，同时计算偏速度和偏角速度。受力分析时，不仅考虑了惯性力和惯性力矩、重力和浮力以及流体动力，还重点分析了波浪力和多体系统的附加质量力，推导了广义主动力和广义惯性力的计算公式，最终将结果代入Kane方程中，得到波浪驱动水下航行器的动力学模型。最后采用4阶龙格-库塔积分算法进行运动仿真，仿真结果表明:在4级海况下，波浪驱动水下航行器的航行速度与缆索长度和航行深度有关。

1）随着缆索长度的减小，航行速度有所提高，但由于缆索长度的不断减小，驱动体将会受到波浪的影响，不利于运动的稳定性，同时在缆索长度为3 m时，驱动体攻角的变化幅度较大，从运动稳定性和使用寿命方面来考虑，本文缆索长度选择为4 m.

2）随着航行器航行深度的减小，整个系统所获得的波浪能有所增加，这将增加整个系统的前进动力，故航行速度有所提高，仿真结果显示在4 m航行深度时，航行速度相对较大，可达到0.47 m/s左右。

本文提出了波浪驱动水下航行器的运动学和动力学模型。但本文同时也存在一些问题需要完善。由于缆索的上端也处于近水面，所以也会受到波浪的影响，这还需要进一步研究。

（References）

［1］ Hine R，Willcox S，Hine G，et al.The wave glider:a wave-powered autonomous marine vehicle［C］∥MTS/IEEE Conference on Marine Technology for Our Future:Global and Local Challenges. Biloxi，Mississippi，US:IEEE，2009.

［2］ Caiti A，Calabro V，Grammatico S，et al.Lagrangian modeling of the underwater wave glider［C］∥IEEE OCEANS Conference. Santander，Spain:IEEE，2011.

［3］ 李小涛.波浪滑翔器动力学建模及其仿真研究［D］.北京:中国舰船研究院，2014:11-53. LI Xiao-tao.Wave glider dynamic modeling and simulation research［D］.Beijing:China Academy of Ships，2014:11-53.（in Chinese）

［4］ Yang K，Wang X Y，Ge T，et al.Dynamic model of underwater snake-like robot using Kane's method［J］.Journal of Shanghai Jiao Tong University:Science，2014，19（2）:146-154.

［5］ Mohan S，Kim J.Coordinated motion control in task space of an autonomous underwater vehicle-manipulator system［J］.Ocean Engineering，2015，104（1）:155-167.

［6］ 贾立娟.波浪动力滑翔机双体结构工作机理与动力学行为研究［D］.天津:国家海洋技术中心，2014:31-38. JIA Li-juan.The study of wave power glider catamaran structure working mechanism and dynamics behavior［D］.Tianjin:National Ocean Technology Center，2014:31-38.（in Chinese）

［7］ 潘光.鱼雷力学［M］.西安:陕西师范大学出版社，2013. PAN Guang.Torpedo mechanics［M］.Xi'an:Shaanxi Normal U-niversity Press，2013.（in Chinese）

［8］ 张宇文.鱼雷弹道与弹道设计［M］.西安:西北工业大学出版社，1999. ZHANG Yu-wen.Torpedo trajectory and trajectory design［M］. Xi'an:Northwestern Polytechnical University Press，1999.（in Chinese）

［9］ Zhang W，Liu X P，Fang C W，et al.Dynamic modeling of a spherical robot with arms by using Kane's method［C］∥Fourth International Conference on Natural Computation.Jinan:IEEE，2008:373-377.

［10］ 常宗瑜，陈秉聪.水下机器人-机械手系统的动力学分析［J］.机械，2006，33（4）:4-6. CHANG Zong-yu，CHEN Bing-cong.Dynamic analysis of the underwater robot manipulator system［J］.Machine，2006，33（4）: 4-6.（in Chinese）

［11］ 夏丹，陈维山，刘军考，等.基于Kane方法的仿鱼机器人波状游动的动力学建模［J］.机械工程学报，2009，45（6）: 41-49. XIA Dan，CHEN Wei-shan，LIU Jun-kao，et al.Dynamics modeling of simulated robot fish swimming wavy based on Kane method［J］.Journal of Mechanical Engineering，2009，45（6）:41-49.（in Chinese）

［12］ Du X X，Song B W，Meng R，et al.Effect of wave to low speed maneuvers of Torpedo-like long-distance AUV［J］.Journal of System Simulation，2008，20（8）:1945-1960.

［13］ 丁浩，宋保维，田文龙.水下仿生扑翼推进性能分析［J］.西北工业大学学报，2013，31（1）:151-155. DING Hao，SONG Bao-wei，TIAN Wen-long.Underwater flapping-wing propulsion performance analysis［J］.Journal of Northwestern Polytechnical University，2013，31（1）:151-155.（in Chinese）

［14］ 刘鹏，苏玉民，刘焕兴.串列异步拍动翼推进性能分析［J］.上海交通大学学报，2004，48（4）:457-463. LIU Peng，SU Yu-min，LIU Huan-xing.Serial asynchronous flapping-wing propulsion performance analysis［J］.Journal of Shanghai Jiao Tong University，2004，48（4）:457-463.（in Chinese）

［15］ 匡建平，吴训涛，王虹旋.细长圆柱体水中无约束运动的附加质量计算方法探析［J］.四川兵工学报，2014，35（6）: 143-145. KUANG Jian-ping，WU Xun-tao，WANG Hong-xuan.Additional quality calculation method for underwater unconstrained motion of elongated cylinder［J］.Journal of Sichuan Ordnance，2014，35（6）:143-145.（in Chinese）

The Multi-body System Dynamics Modeling of Wave-driven Underwater Vehicle Based on Kane Method

DU Xiao-xu1，CUI Hang1，XIANG Zhen-hui2
（1.School of Marine Science and Technology，Northwestern Polytechnical University，Xi'an 710072，Shaanxi，China；2.Kunming Shipbuilding Equipment Co.，Ltd，Kunming 650051，Yunnan，China）

A coordinate system for wave-driven underwater vehicle is defined based on multi-body system dynamics theory.The kinematics analysis of the whole system is performed by choosing the appropriate generalized coordinates，while the velocities and acceleration are deduced，and the expressions of partial velocities and partial angular velocities are deduced based on Kane's method according to the dynamic analysis of the whole system.The generalized inertial force and generalized active force of the whole system are calculated.A multi-body system dynamics model of wave-driven underwater vehicle is established by taking the calculated results into the Kane's equations.The force analysis of the proposed model focuses on the wave force and the additional mass force of multi-body system besides inertia force，inertia moment，gravity，buoyancy and hydrodynamic forces.The wave-driven underwater vehicle is simulated. The simulated results show that the proposed modeling method is valid.

ordnance science and technology；Kane equation；wave-driven underwater vehicle；multibody system dynamics

TJ630.1

A

1000-1093（2016）07-1236-09

10.3969/j.issn.1000-1093.2016.07.011

2015-12-21

国家自然科学基金项目（11302176）；高等学校博士学科点专项科研基金项目（20126102120021）；中央高校基本科研业务费基础研究项目（3102014JCQ01006）

杜晓旭（1981—），男，副教授，硕士生导师。E-mail:nwpudu@163.com；

崔航（1993—），男，硕士研究生。E-mail:nwpucuihang@163.com；

向祯晖（1982—），男，工程师。E-mail:xianghui990660@163.com