基于Matlab的不同数字滤波器对语音信号的去噪效果

赵培瑶 向凤红 毛剑琳 郭 宁 孔庆平

(昆明理工大学信息工程与自动化学院,昆明 650500)

基于Matlab的不同数字滤波器对语音信号的去噪效果

赵培瑶 向凤红 毛剑琳 郭 宁 孔庆平

(昆明理工大学信息工程与自动化学院,昆明 650500)

基于Matlab软件平台研究了不同的数字滤波器对污染的语音信号的去噪效果。对比了加入噪声前后的语音信号的时域与频域图。仿真实验结果表明：4种滤波器中切比雪夫I型滤波器对加入噪声后的语音信号的去噪效果最佳，且成功滤除了高频噪声。

信号去噪 数字滤波器 语音信号 Matlab

在信号处理过程中，所处理的信号常混有噪音，从接收到的信号中消除或减弱噪音是信号处理和传输中一个十分重要的课题[1,2]。数字滤波器是一种可以通过一定运算关系使输入信号(离散时间信号)中频率成分的相对比例改变或者滤除输入信号中某些频率成分的器件[3,4]。数字滤波器可分为两类：有限脉冲响应(Finite Impulse Response,FIR)数字滤波器和无限脉冲响应(Infinite Impulse Response,IIR)数字滤波器。FIR数字滤波器具有稳定性好、精度高、累积误差小及易于计算机辅助设计等优点；但存在计算量大的缺点。IIR数字滤波器具有结构简单、效率高、与模拟滤波器有对应关系、易于解析控制及计算机辅助设计等优点；缺点是稳定性较差，易产生溢出、噪声和误差[5～7]。2011年，谢黎明和郑锐设计了一种基于Matlab的IIR数字滤波器，分析表明，该IIR数字滤波器具有良好的去噪性能[8]。2012年，张廷尉等设计了一种基于Matlab的巴特沃斯数字低通滤波器，并对一段音频信号进行了滤波去噪处理，去噪后的音频信号听觉效果变得更加低沉[9]。

在此，笔者基于Matlab仿真软件研究了不同的数字滤波器对污染的语音信号的去噪效果，以得到各数字滤波器的性能，提高对语音信号中噪声的滤除质量。

1 原始语音信号及其Matlab采样①

预先录制一段语音，内容为“基于Matlab的语音信号处理及特性分析”，人声的频率范围为0.3～3.0kHz，则3.0kHz以上的频率分量属于在采集过程中由于设备和环境而引入的噪声。由于人声的频率范围低于3.0kHz，且通过观察原始信号频谱发现，5.0kHz的频率分量能量较小，同时如果噪声频率过高，超过人耳的听力范围，就不能察觉加入的噪声，因此选择添加频率为5.0kHz的高频余弦噪声。如图1所示，使用subplot函数将加入噪声前后的信号时域与频域图绘制在一起，与原始信号对比，加入噪声后信号能量明显变大，且在频率5.0kHz处能量有了很大的增强。使用sound函数播放加入噪声后的语音信号发现，由于余弦噪声的加入，语音背景出现了尖锐鸣声，其尖锐程度取决于余弦噪声的频率。余弦噪声是单一频率的、高频的，因此为了滤除噪声，只需将带有噪声的语音信号通过一个低通滤波器，就可以将余弦噪声和录制过程中引入的噪声滤除。

利用Matlab的wavread函数([x1,fs]=wavread)(fs表示采样频率，单位Hz)对加入噪声的语音信号进行采样，采集原始语音信号的波形和频谱，将采样值放在向量x1中。采样得到的加入噪声的语音信号的功率谱密度估计图如图2所示。

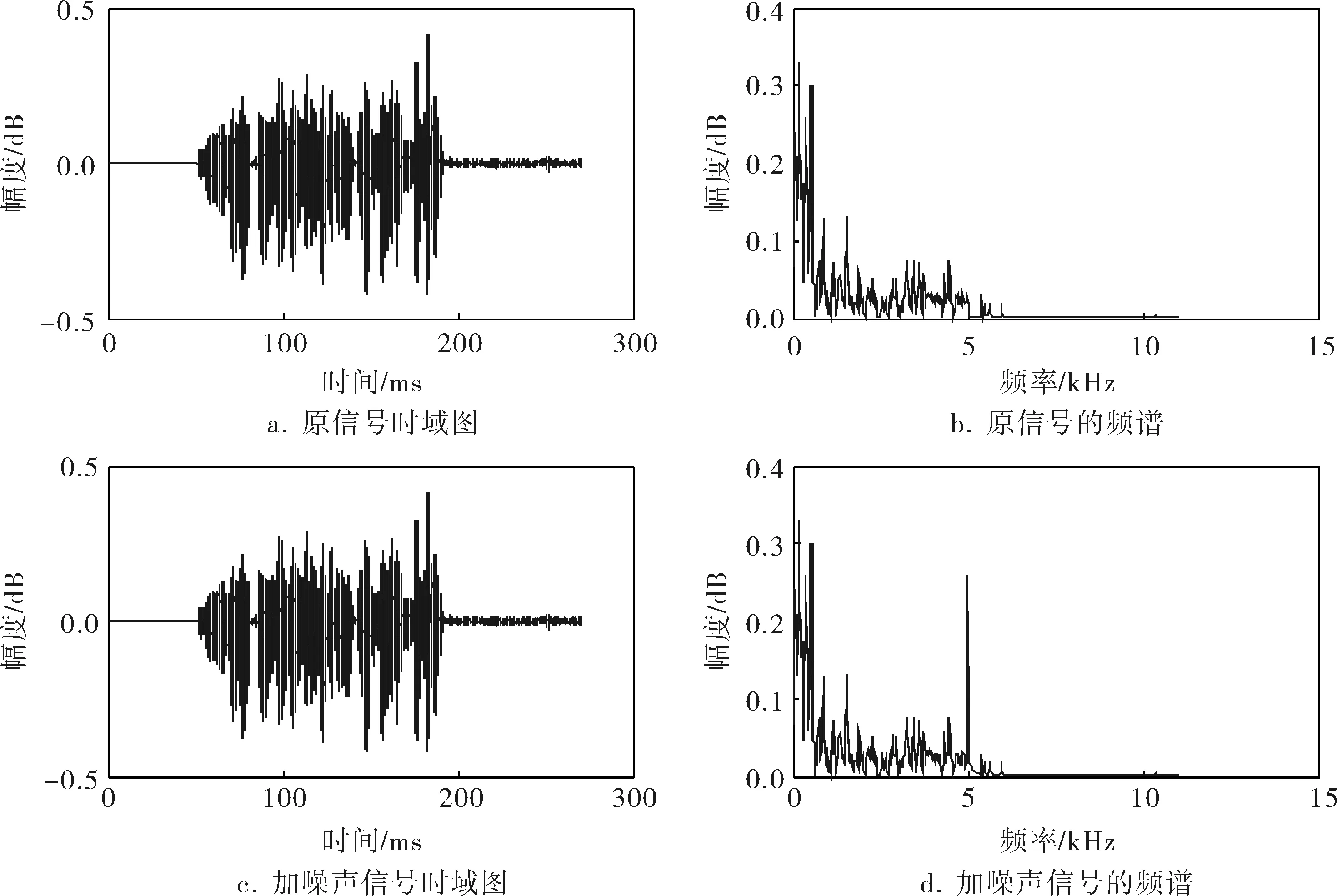
图1 加入噪声前后语音信号的时域与频域图

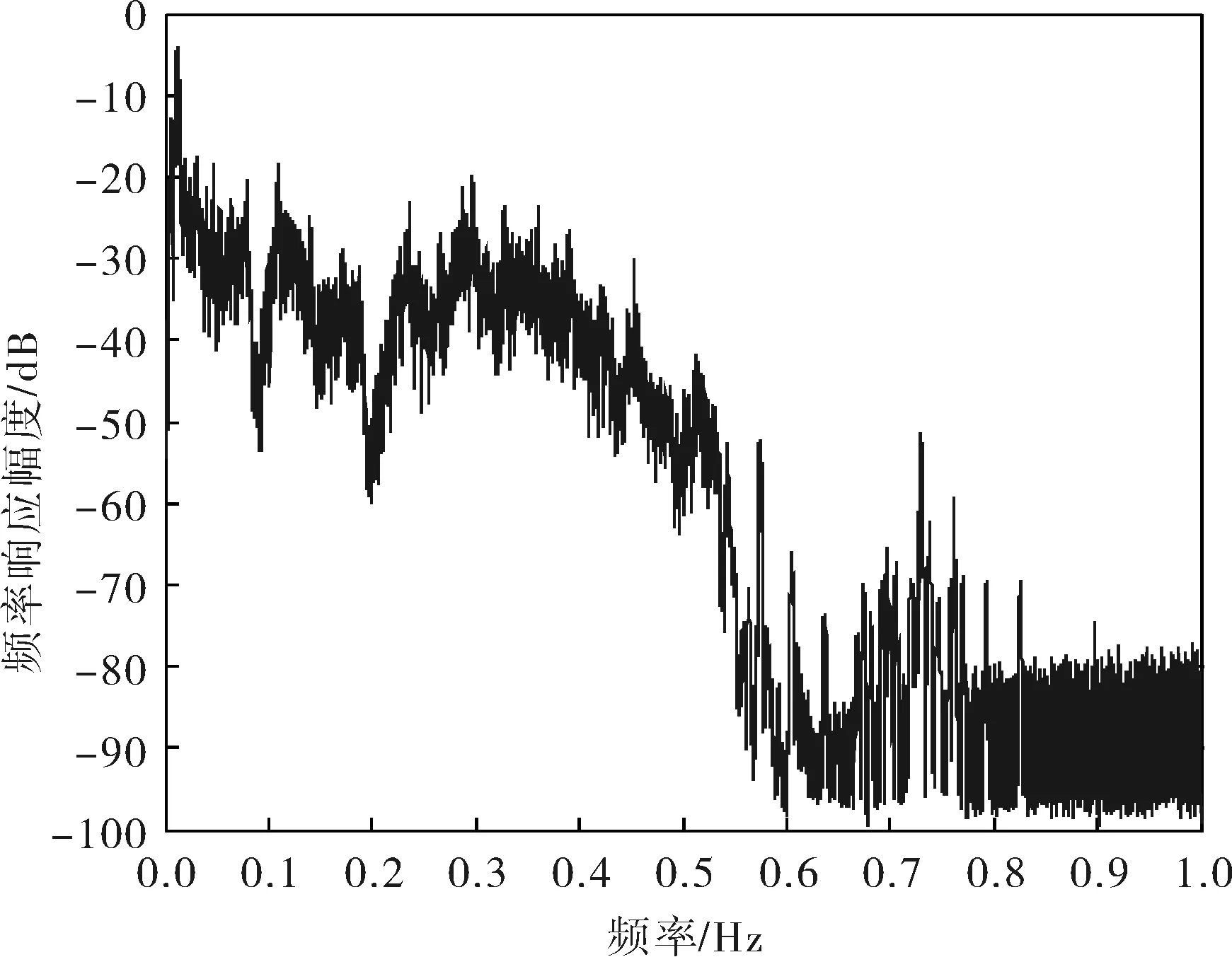
图2 加入噪声的语音信号的功率谱密度估计图

2 4种滤波器的去噪效果

基于Matlab分别使用巴特沃斯滤波器、切比雪夫I型滤波器、切比雪夫II型滤波器和椭圆滤波器对加入余弦噪音的语音信号进行滤波，并绘制出4种滤波器的频率响应曲线，如图3所示。可以看出，巴特沃斯滤波器在通带内具有最大平坦的幅度特性，而且随着频率升高呈现出单调减小的特点；切比雪夫Ⅰ型滤波器在通带内是等波纹的，在阻带内是单调的；切比雪夫Ⅱ型滤波器在阻带内是等波纹的，在通带内是单调的；椭圆滤波器在通带内和阻带内都具有等波纹振幅特性。可见，切比雪夫Ⅰ型滤波器的去噪效果最佳，因此采用切比雪夫Ⅰ型滤波器对噪声信号进行低通滤波，去除高频噪声干扰，并绘制去噪后语音信号的功率谱密度估计图如图4所示。

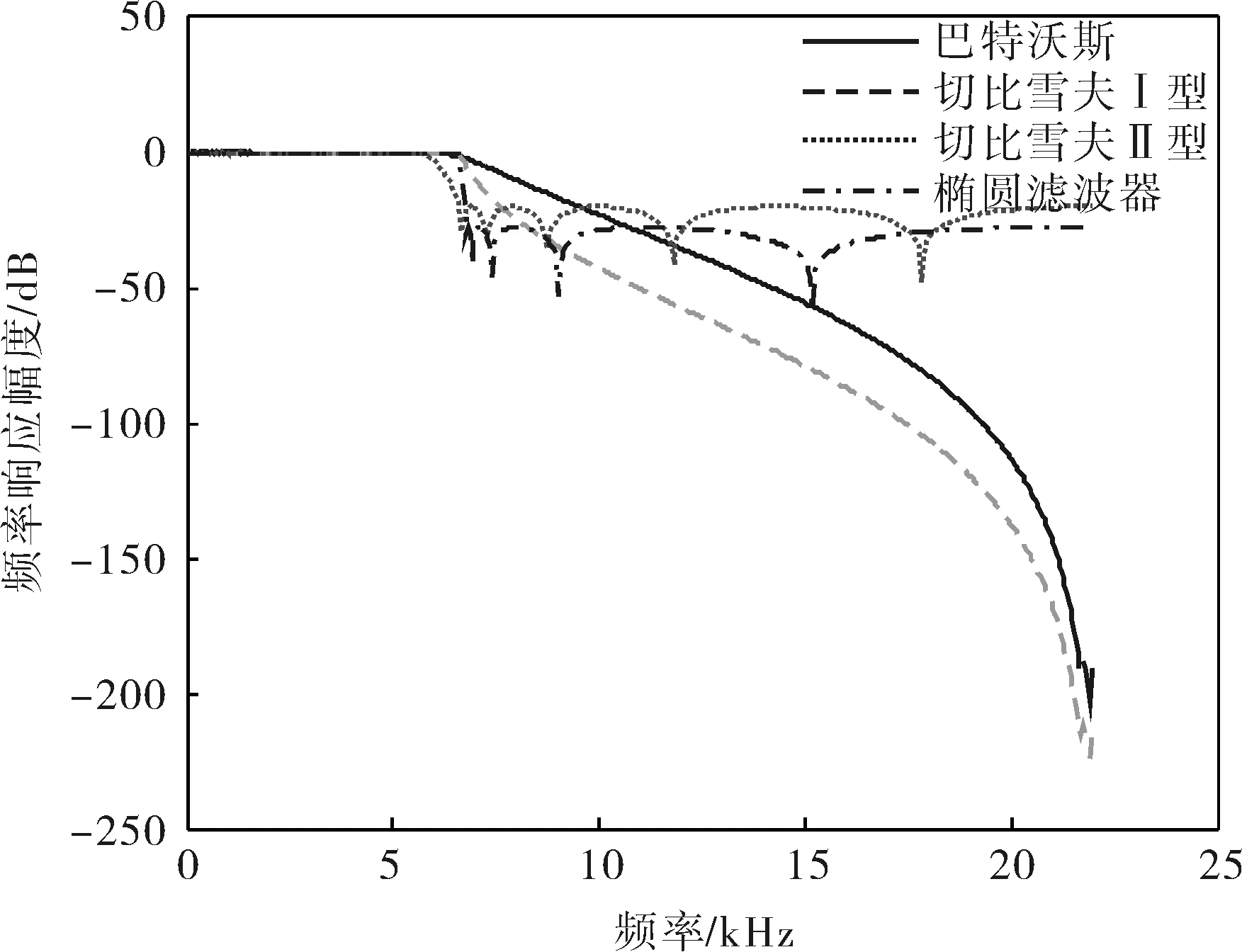
图3 4种滤波器的频率响应曲线

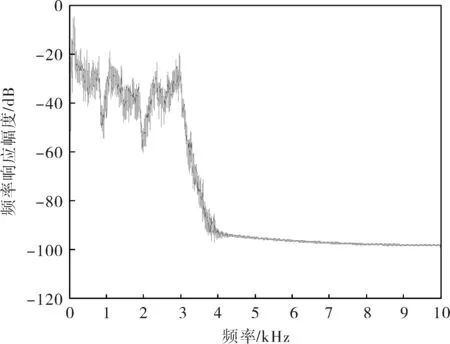
图4 去噪后语音信号的功率谱密度估计图

由图4可以看出，通过切比雪夫Ⅰ型滤波器后，频率高于3.0kHz的信号被截止，低频的语音信息被保留下来，由设备、环境而引入的噪声和加入的余弦噪声均被滤除。播放过滤后的语音信号已经听不到尖锐的高频声音，证明噪声被成功滤除，基本还原原始信号，达到了滤除高频噪声的目的。

3 结束语

笔者基于Matlab软件平台研究了4种不同的数字滤波器对污染的语音信号的去噪效果。仿真实验结果表明，切比雪夫Ⅰ型滤波器对语音信号的去噪效果最佳，通过对噪音信号进行数字滤波处理，滤除了噪声频率成分，得到了纯净的语音信号，提高了语音信号质量。同时，语音信号噪声滤除实验中，4种数字滤波器的仿真实验数据与效果对比，为业内人士在今后的滤波器选择方面提供了一定的参考依据。

[1] 赵颖,刘祖深,李胜寅.基于MATLAB的FIR数字滤波器的方法设计[J].国外电子测量技术,2012,31(10):35～37.

[2] 严慧,于继明.基于Matlab的IIR数字滤波器设计[J].软件导刊,2013,12(1):110～113.

[3] 徐红,李刚,黄朝耿,等.一种设计IIR数字滤波器的参数化方法[J].电子学报,2012,40(4):847～851.

[4] 张萍.基于DSP的IIR低通数字滤波器的设计与实现[J].江南大学学报(自然科学版),2014,13(1):67～71.

[5] 张军辉,李响.改进的粒子滤波算法性能分析[J].郑州轻工业学院学报(自然科学版),2009,24(2):73～75.

[6] 李兰英,王志超,王峰,等.FIR数字滤波器设计与仿真[J].哈尔滨理工大学学报,2013,18(3):36～41.

[7] 夏永泉,徐洁,崔伟.均值滤波中邻域均值的快速计算[J].郑州轻工业学院学报(自然科学版),2008,23(3):57～59.

[8] 谢黎明,郑锐.基于Matlab的IIR数字滤波器设计[J].机械与电子,2011,(1):28～30.

[9] 张廷尉,陈红,王磊.基于Matlab的巴特沃斯数字低通滤波器的设计[J].鞍山师范学院学报,2012,14(2):13～15.

AbstractBoth single water tank and rectification column was taken as simulation objects, in which, the prediction control model was applied; basing on Matlab simulation, the minimum variance method was adopted to improve MPC’s control performance. As for the multivariable system of the rectification column model, the historical performance index and the design performance index, including the residual cumulative sum and control charts were adopted to monitor MPC performance. The results verify effectiveness of the method proposed.

KeywordsMPC, dynamic matrix algorithm, minimum variance, performance assessment, Matlab

De-noisingEffectsofDifferentMatlab-basedDigitalFiltersforVoiceSignals

ZHAO Pei-yao, XIANG Feng-hong, MAO Jian-lin, GUO Ning, KONG Qing-ping

(FacultyofInformationEngineeringandAutomation,KunmingUniversityofScienceandTechnology,Kunming650500,China)

Having Matlab based to investigate different digital filter’s effect in de-noising voice signals was implemented and the time domain and the frequency range charts before and after introducing the noise were compared. Simulation results show that, the Chebyshev Ⅰ filter of four filters has best effect in de-noising voice signals and the high-frequency noise there can be filtered completely.

signal de-noising, digital filter, voice signal, Matlab

(Continued from Page 711)

XIAO Zhen, GAO Qiang, CHANG Yong

(TianjinKeyLaboratoryforControlTheoryandApplicationinComplicatedSystems,TianjinUniversityofTechnology,Tianjin300384,China)

2015-11-30(修改稿)

国家自然科学基金项目(61163051)

TH865

A

1000-3932(2016)07-0717-03