模型预测控制系统的性能评价研究

肖 振 高 强 常 勇

(天津理工大学天津市复杂系统控制理论及应用重点实验室,天津 300384)

模型预测控制系统的性能评价研究

肖 振 高 强 常 勇

(天津理工大学天津市复杂系统控制理论及应用重点实验室,天津 300384)

以单容水箱、精馏塔为仿真对象，以模型预测控制作为实现过程，通过Matlab仿真方式，利用最小方差法进一步提高单容水箱单变量模型的预测控制性能；对精馏塔模型多变量系统，利用历史性能指标和设计性能指标，以残差的累积和图为手段进行模型预测控制性能监视，最后验证了所提方法的有效性。

模型预测控制系统 动态矩阵算法 最小方差 性能评价 Matlab

模型预测控制(Model Predictive Control,MPC)产生于20世纪70年代，是先进工业过程控制领域中一类计算机控制算法。因MPC可将控制系统接近到约束边界附近并达到提高经济效益的目的，因此被广泛应用于炼油、化工等复杂过程工业中。MPC作为一种复杂工业过程控制和优化的有效手段，在工业投入运行初期可以获得良好的性能，但在运行一段时间后，其控制性能会逐渐变差，损害企业利益[1]。因此，使用一定的评价理论监测控制器性能是否下降，确定性能恶化程度，已成为当前控制领域研究的一大热点[2]。

为了提高控制器的控制效果，邹涛等深入研究了鲁棒预测控制和自适应预测控制，重点提出并研究了新算法；同时对控制系统参数整定的可维护性进行了研究，提出通过实时在线的方式监测和评价MPC系统的性能[3]。在此，笔者以MPC控制系统作为控制对象，对其单变量和多变量系统进行性能评价理论的研究，并分别以单容水箱与精馏塔作为仿真对象，验证所提方法的有效性。

1 MPC①

1.1 基本原理

MPC算法以计算机理论为基础，其算法流程一般为：在采样时刻，将测得的被控变量加上预测模型所得出的预测值，以优化性能指标为目标在一定时域内进行控制增量的优化计算，以此求出开环最优问题[4]；将求解出的控制增量序列的首个控制增量应用于被控系统，再利用反馈校正对预测模型进行修正，到下个采样时刻将修改后的预测值与预测模型代入系统中继续求解。MPC原理如图1所示。

图1 MPC原理

动态矩阵控制算法的预测模型以被控系统的阶跃响应为基础，结合实时监测进行滚动优化，并加以反馈校正来进行修正[5]。

1.2预测模型

利用当前系统的历史数据结合未来的控制输入得到未来输出。依据预测模型可以观察输出在不同控制策略下的变化，从而得到不同控制策略的控制效果，并作以比较。基于模型的预测如图2所示。

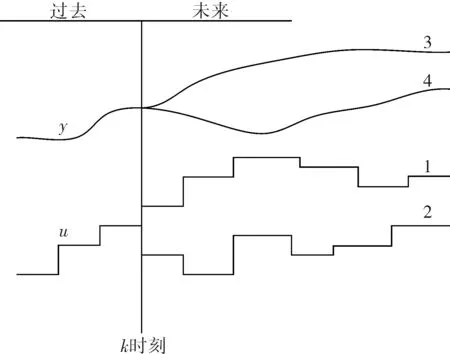
图2 基于模型的预测

1.3滚动优化

滚动优化是MPC优越于其他控制理论的一项重要特点，即MPC在每个控制周期都要根据优化指标对控制增量进行一次优化计算(图3)，因此能够充分考虑模型失配、时变及外部扰动等的影响，不断计算优化，达到最优控制效果。

1.4反馈校正

为了克服系统外界干扰与系统的不确定性，MPC加入反馈校正环节，以维持闭环系统的稳定性。反馈校正在控制周期后将实际输出与预测值比较并得到误差值，再用误差值去修正预测输出值，因此MPC是将滚动优化与反馈校正相结合并反复进行的。误差修正的原理如图4所示[6]。

图3 不同时刻的滚动优化

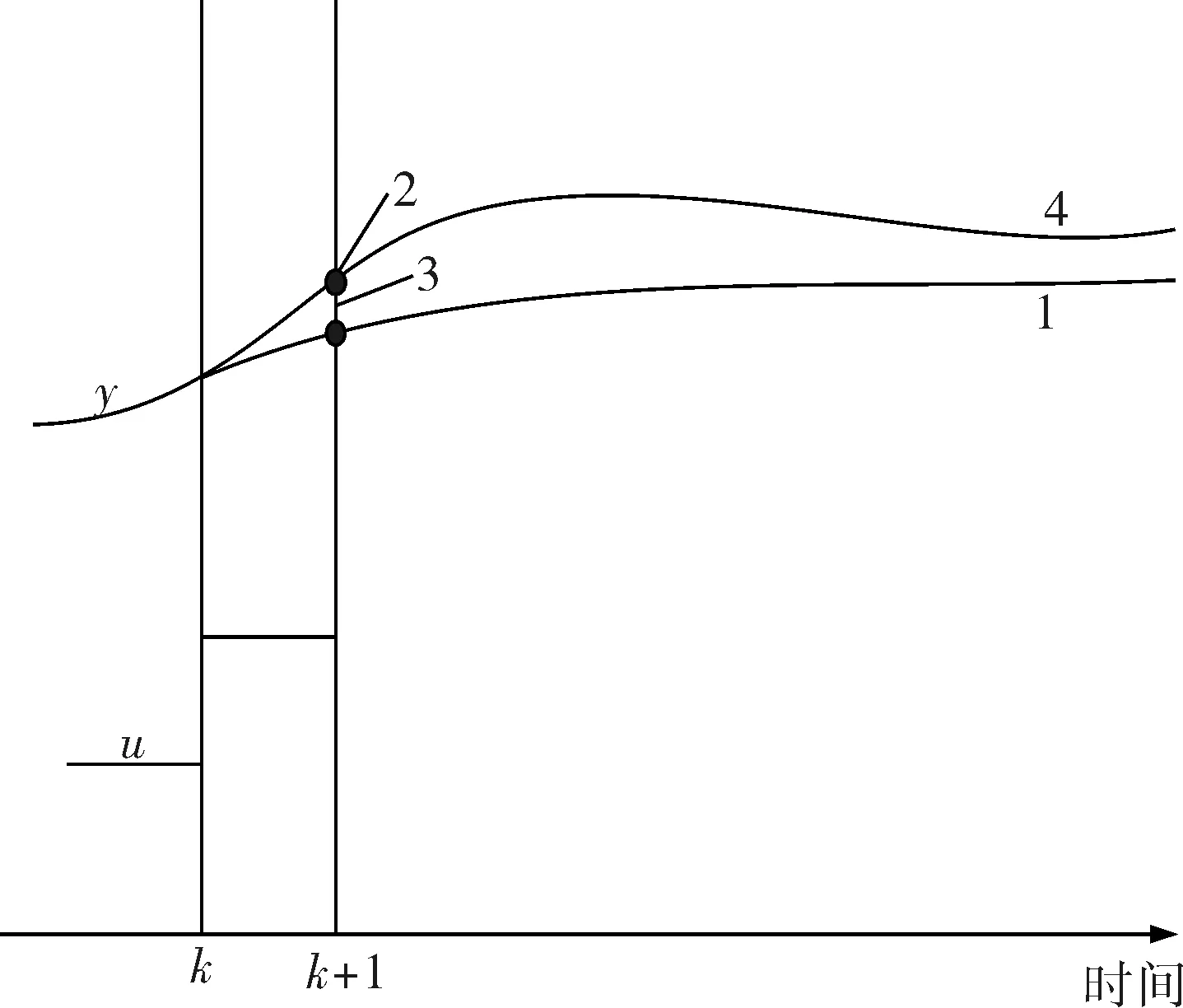
图4 误差修正原理

2 基于最小方差的单变量MPC系统评价

2.1最小方差控制性能评价算法

对如图5所示的单入单出控制系统进行分析，其中Gp是过程对象传递函数，Gl是噪声扰动传递函数，Gc是控制器的传递函数，et是一组零均值的白噪声，ut是输入信号。

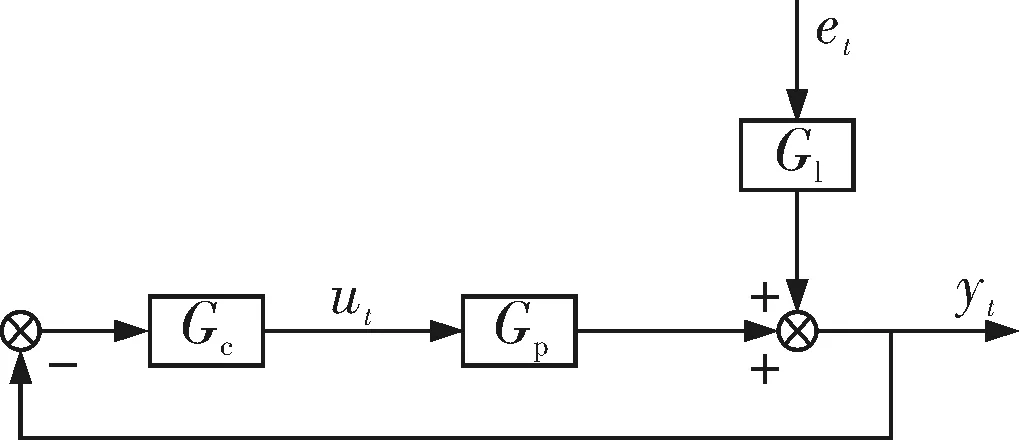
图5 单入单出控制系统框图

系统输出量yt为：

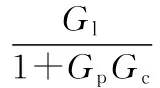
(1)

利用丢番图方程展开如下：

(2)

其中，fi(i=0,1,…,d-1)是Gl的单位脉冲响应系数，R是剩余合理的传递函数。

将式(2)代入式(1)得：

(3)

=Fet+Let-d

由于Fet是独立的白噪声时间序列，因此式(3)中等号右侧的两部分是相互独立的，作为一个结果可表示为：

Var(yt)=Var(Fet)+Var(Let-d)

(4)

因此Var(yt)≥Var(Fet)。当且仅当L=0时取得等号，即：

(5)

因此得到最小变量控制的控制器传递函数为：

(6)

其中，F是系统的传递函数，所以Fet的输出是在最小方差控制下的过程输出，即Fet在系统反馈中是不变的。

又考虑到闭环日常运行数据是有效的，为了克服随机量的耦合性，运用时间序列分析，建立不同形式的模型等式，进行二次z变换，则不同的等式写成离散时间传递函数为：

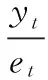
(7)

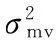
(8)

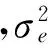
2.2实验仿真分析

以单容水箱模型的液位控制系统为研究对象，其动态特性常表现为大惯性和滞后性。针对MPC的DMC算法，利用Matlab的MPC工具箱，对系统添加白噪声扰动并进行分析。基于MPC控制器的单容水箱Simulink仿真模型如图6所示。

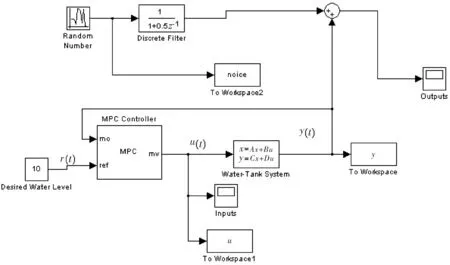
图6 基于MPC控制器的单容水箱Simulink仿真模型

2.3单容水箱MPC数学模型的建立

首先采用Matlab的MPC工具箱建立系统模型并转换系统函数，完成各模型之间的相互转换，然后创建系统的数学模型，在工作空间定义并记作WaterModel，接着应用MPC工具箱中的GUI工具对控制器进行设计。

按照上述步骤，在Matlab中使用函数辨识输出数据得到系统模型为：

State-space model:x(t+Ts)=Ax(t)+Ke(t)

y(t)=Cx(t)+e(t)

A=x1 x2 x3

x1 0.99215 -0.0078815 0.013997

x2 0.0083576 -0.2056 -0.53377

x3 0.038632 -0.2179 -0.34158

C=x1 x2 x3

y1 -2.4168 -2.047 -0.83695

K= y1

x1 -0.022481

x2 0.30819

x3 0.0033448

x(0)=x1 1.1205,x2 7.982,x3 -9.4862

根据系统阶跃输出信号可以得到动态矩阵控制中的预测模型，因此对MPC控制器进行设计时，必须要知道被控系统阶跃响应的相关情况，以此验证模型的可靠性。对被控系统和单位阶跃响应模型描述的系统分别输入正弦信号u=sin(t)，得到随时间的变化曲线如图7所示，可以看出所建立模型的理论输出信号与系统的实际输出信号基本相同，验证了模型的可靠性。

图7 阶跃响应模型的输出响应

2.4MPC控制器参数调节

动态矩阵算法中的预测模型是根据辨识模型获得的，通过限制预测模型进行参数调节，单容水箱的MPC控制器参数如下：

优化时域P250

控制时域M100

误差加权矩阵Q0.017 5

控制作用加权矩阵R0.75

控制时间间隔 0.4

2.5实际系统控制效果

建立单容水箱模型后，通过对控制仿真前的模型可预测性和可靠性的验证，以及对模型参数的调节，最后利用Simulink对系统进行仿真，得到波形图如图8所示。

由图8可知，曲线1含噪高，不平稳、不光滑，控制器控制效果较差，应对MPC控制器重新进行调节；而曲线2是经过最小方差基准进行改进后的MPC控制曲线，该曲线更平滑，控制效果得到提升。

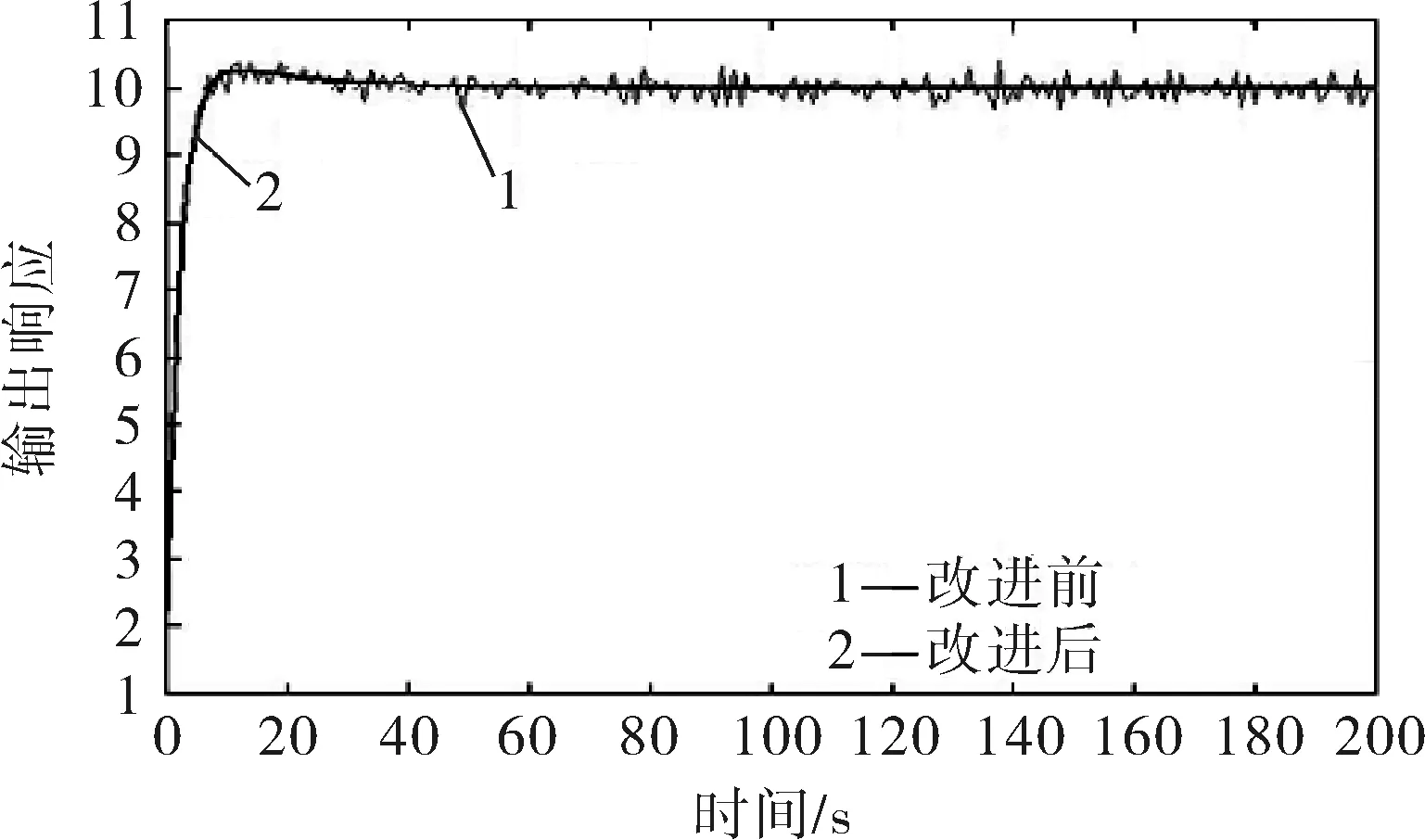
图8 控制性能对比分析曲线

则基于最小方差基准的曲线1和曲线2评价结果分别为：

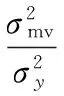
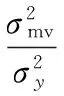
通过数据可以看出，曲线2的输出更接近1，说明经过最小方差基准进行改进后MPC控制器性能更好，验证了算法的有效性。

3 基于历史性能指标和设计性能指标的MPC系统评价

3.1MPC性能指标评价法

根据模型预测的基本原理，可以把MPC目标函数写做：

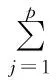
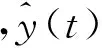
性能指标可以写成：

J(t)=εT(t)Qε(t)+ΔuT(t)RΔu(t)

其中，ε(t)是被控变量。

根据上述基本原理的描述，引入历史性能指标与设计性能指标评价方法。

依照专家经验评估系统在一段时间内的性能，进而应用目标函数得到一个标准，再利用被控系统实际工作的数据计算出目标函数值。则历史最优目标函数值与可获得的目标函数值的比即为历史性能指标：

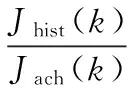
设计最优目标的函数值与可获得的目标函数值的比即为设计性能指标：

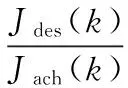
模型设计预测控制时会获得设计目标函数值，设计性能指标就是利用这一数值作为标准。

3.2MPC系统的在线监视

在系统利用基于数据统计的评价方法时，由于针对系统外数据的分析处理，并没有对系统的操纵变量做过多处理，因此对控制器寿命的增加和经济利益的增长具有很大优势。

然而由于随机噪声的影响，在利用历史性能指标监控系统的过程中，随机量的自相关现象严重，为了解决这一问题提出了时间序列分析法。使用该方法时首先由过程稳态下自相关的观测值来预估时间序列模型，然后根据时间序列模型得到预测值，再与实际输出比较得到两者的残差。时间序列分析法在保证得到的时间序列模型是准确的情况下，使最终的残差序列是互不干扰的，此时再用传统的统计方法实现系统监控是可行的。

一般情况下，用自回归模型的形式来表示MPC的性能，即：

A(q-1)η(k)=ε(k)

其中，A(q-1)是一个系数为ai(i=1,2,…,na)的多项式，ε(k)是高斯白噪声。MPC的性能可以利用该模型估计，即：

3.3仿真实例

3.3.1仿真对象

精馏塔模型是一个典型的具有多个束缚条件的多变量过程模型。精馏塔仿真系统的数学模型为：

Y(s)=G(s)u(s)+N(s)d(s)

(9)

其主要输入输出变量之间的传递函数用一阶惯性加纯滞后的形式表示，其矩阵形式的模型可分为两个部分，一个是过程模型G(s)，另一个是过程的干扰模型N(s)：

(10)

(11)

其中，y1为轻馏分，y2为重馏分，u1为蒸发器流量，u2为回流冷凝器流量，u3为进料的可测扰动，d1(s)、d2(s)为干扰模型的不可测扰动变量。塔顶馏分与塔底馏分的组分浓度作为动态矩阵控制器的被控变量，回流冷凝器流量和再沸器流量作为动态矩阵控制器的操作变量，进料流量的波动作为被控系统的可测干扰量[8]。

则MPC问题可描述如下：

u3sp)2

约束满足：-0.5≤y1,k+j≤0.5,-5≤y2,k+j≤5,1≤j≤P,-0.5≤u1,k+j≤0.5,1≤j≤M-1,-0.5≤u2,k+j≤0.5,1≤j≤M-1,-0.5≤u3,k+j≤0.5,1≤j≤M-1。

3.3.2仿真过程

实验应用Matlab仿真软件中自带的MPC工具箱设计MPC控制器，控制器的预测模型见式(9)，参数配置如下：

优化时域P50

控制时域M2

误差加权矩阵Q1.45

控制作用加权矩阵R1.5

控制时间间隔 1.0

为了对历史性能指标法在MPC控制器评价中的可行性进行验证，对模型人为添加干扰，并进行对比分析。在运行初期阶段，模型运行于标准模型附近，系统的控制性能非常稳定。当系统运转一段时间后，其性能指标显著下降，监视指标残差也超出了控制限度。图9为增大增益1.5倍后的历史性能指标统计图，图10为设计性能指标的统计图。

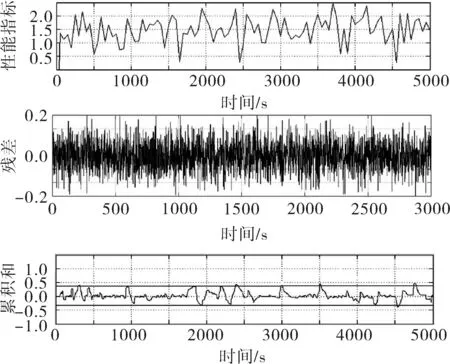
图9 增大增益1.5倍后的历史性能指标统计图

图10 增大增益1.5倍后的设计性能指标统计图

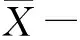
4 结束语

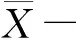
[1] Ender D B.Process Control Performance:Not as Good as You Think[J].Control Engineering Practice,1993,40(10):180～190.

[2] 金晓明,王树青,荣冈.先进控制技术及应用第四讲模型预测控制及其工业应用[J].化工自动化及仪表,1999,26(5):67～74.

[3] 邹涛,丁宝苍,张端.模型预测控制工程应用导论[M].北京:化学工业出版社,2010.

[4] 钱积新,赵均,徐祖华.预测控制[M].北京:化学工业出版社,2007.

[5] 董洪霞.动态矩阵控制算法的改进及其仿真研究[D].鞍山:辽宁科技大学,2012.

[6] Sun Z J,Qin S J,Singhal A,et al.Performance Monitoring of Model-Predictive Controllers via Model Residual Assessment[J].Journal of Process Control,2013,23(4):473～482.

[7] 张新颖,金慰刚,张建华,等.基于最小方差准则的控制系统性能评价[J].现代电力,2006,23(6):73～75.

[8] 朱先桃,张美玉,杨马英,等.最小方差准则在精馏塔控制器性能分析中的应用[J].石油化工自动化,2003,39(6):17～20.

ResearchonPerformanceEvaluationofModelPredictionControlSystem

(Continued on Page 719)

2015-11-30(修改稿)

天津市中青年骨干创新人才培养计划项目(20130830)

TH865

A

1000-3932(2016)07-0706-07