第三类切比雪夫型方程组的通解

曹嘉芮， 吴 康

(华南师范大学 数学科学学院，广东 广州 510631)

第三类切比雪夫型方程组的通解

曹嘉芮， 吴 康

(华南师范大学 数学科学学院，广东 广州 510631)

定义了第三类切比雪夫型一元方程(组)，通过各个方程根的两两配对，得到二阶乃至高阶方程组通解的表达形式.

第三类；切比雪夫型方程(组)；方程根；通解；高阶

1 预备知识

第一类切比雪夫多项式(Tn(x))和第二类切比雪夫多项式(Un(x))是以俄国著名数学家切比雪夫(Tschebyscheff)的名字命名的特殊函数[1-2]，起源于多倍角的余弦函数和正弦函数的展开式，是当前研究的一个热点并且应用广泛.

目前对第一类、第二类切比雪夫型方程组的通解[3-6]有一定的研究，但对第三类切比雪夫方程组的通解问题尚未研究，本文基于切比雪夫多项式的实用性，对第三类切比雪夫型方程(组)进行深入的研究.

定义[7-8]第三类切比雪夫多项式序列{Vn(x)}定义为

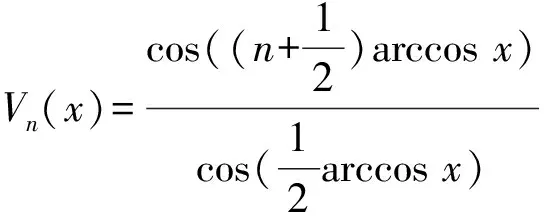
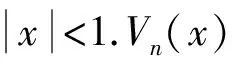
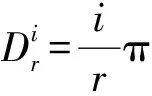
2 引理

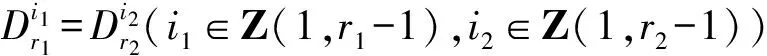
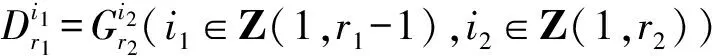
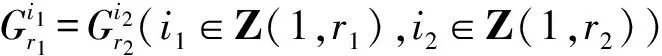
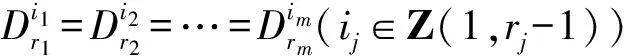
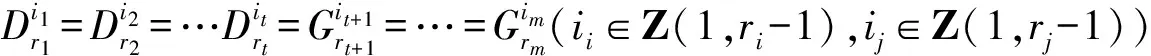
3 第三类切比雪夫型方程(组)

3.1 第三类切比雪夫型方程

定义1 设n,m∈N,n>m,称方程Vn(x)=Vm(x)为第三类切比雪夫型一元方程.

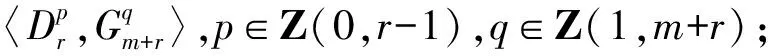
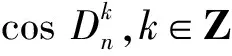
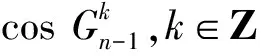
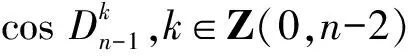
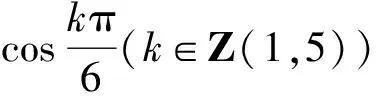
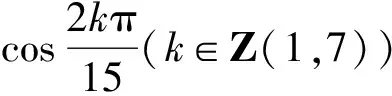
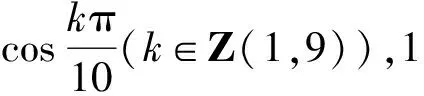
3.2 第三类切比雪夫型一元二阶方程组

定义2 设n1,n2,m1,m2∈N,n1>m1,n2>m2,称方程组

(1)

为第三类切比雪夫型一元二阶方程组.

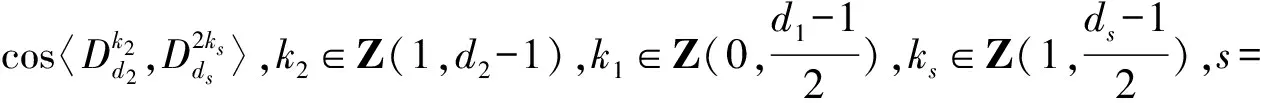
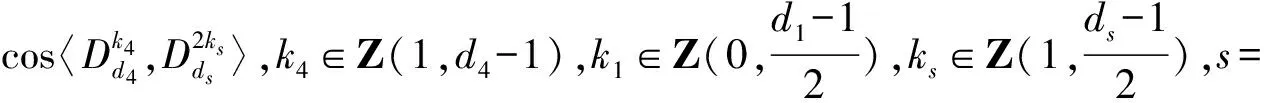
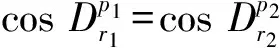
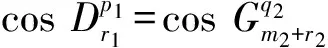
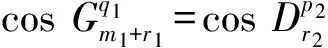
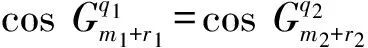
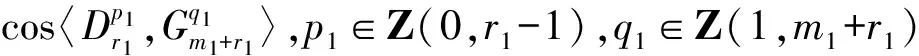
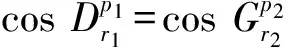
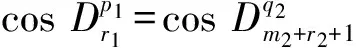
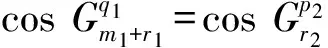
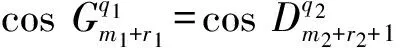
3)同情况2)，不详述.

4)若n1-m1=2r1+1,n2-m2=2r2+1,此时方程组第i个方程的复数根为

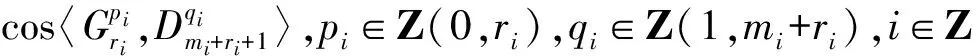
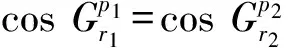
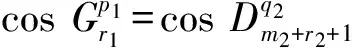
③同②，不详述.

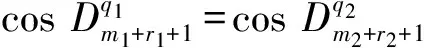
3.3 第三类切比雪夫型一元三阶方程组

定义3 设n1,n2,n3,m1,m2,m3∈N,n1>m1,n2>m2,n3>m3,称方程组

(2)

为第三类切比雪夫型一元三阶方程组.

1)若n1-m1=2r1,n2-m2=2r2,n3-m3=2r3,令d1=(a11,a21,a31),d2=(a11,a21,a32),d3=(a11,a22,a31),d4=(a11,a22,a32),d5=(a12,a21,a31),d6=(a12,a21,a32),d7=(a12,a22,a31),d8=(a12,a22,a32)，

2)若nj-mj=2rj,nk-mk=2rk,nl-ml=2rl+1,j,k,l=〈1,2,3〉且j≠k≠l,令

d1=(aj1,ak1,bl1),d2=(aj1,ak1,bl2),d3=(aj1,ak2,bl1),d4=(aj1,ak2,bl2),d5=(aj2,ak1,bl1),d6=(aj2,ak1,bl2),d7=(aj2,ak2,bl1),d7=(aj2,ak2,bl2)，

此时方程的解为

3)若nj-mj=2rj,nk-mk=2rk+1,nl-ml=2rl+1,j,k,l=〈1,2,3〉且j≠k≠l,令

d1=(aj1,bk1,bl1),d2=(aj1,bk1,bl2),d3=(aj1,bk2,bl1),d4=(aj1,bk2,bl2),d5=(aj2,bk1,bl1),

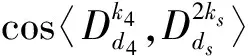
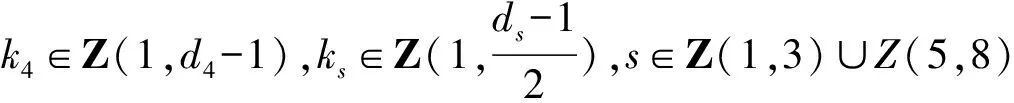
4)若nj-mj=2rj+1,nk-mk=2rk+1,nl-ml=2rl+1,j,k,l∈〈1,2,3〉且j≠k≠l,

令d1=(bj1,bk1,bl1),d2=(bj1,bk1,al2),d3=(bj1,ak2,bl1),d4=(bj1,ak2,al2),d5=(aj2,bk1,bl1),

d6=(aj2,bk1,al2),d7=(aj2,ak2,bl1),d8=(aj2,ak2,al2)，

此时方程的解为

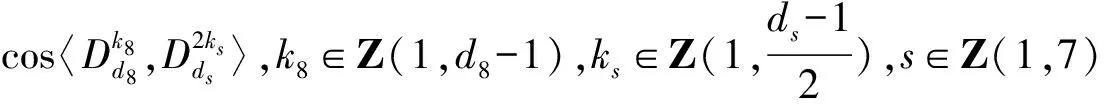
证明 1)若n1-m1=2r1,n2-m2=2r2,n3-m3=2r3,此时方程组第i个方程的复数根为

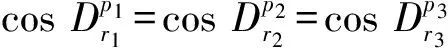
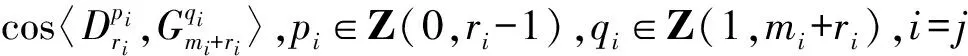
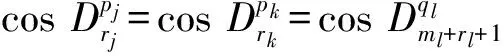
3)证明同情况2),不详述.

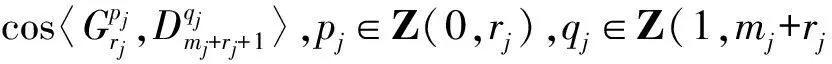
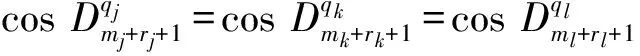
3.4 第三类切比雪夫型一元r阶方程组

定义4 设ni,mi,∈N,ni>ml,称方程组

(3)

为第三类切比雪夫型一元r阶方程组.

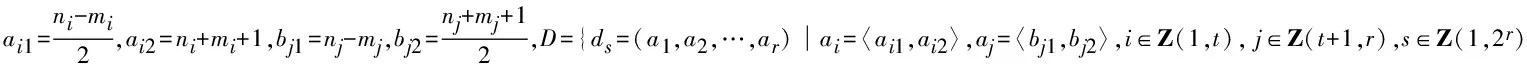
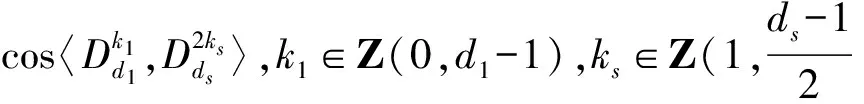
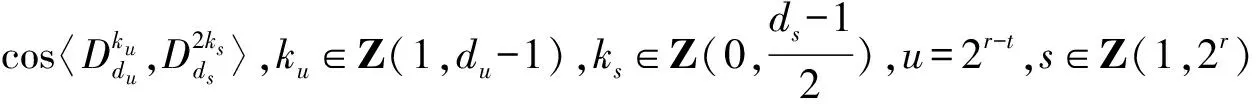
证明 1)若t=r,则ni-mi=2ri,ri∈Z(1,r),此时方程组第i个方程的复数根为

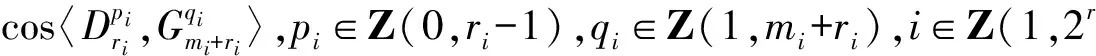
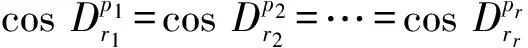
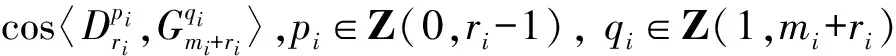
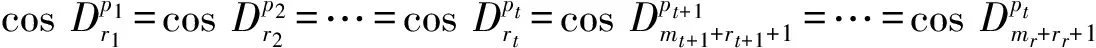
3.5 第三类切比雪夫型一元高阶方程组的应用

[1] 叶其孝，沈永欢.实用数学手册[M]. 2版.北京：科学出版社，2006:687-689.

[2] 《数学手册》编写组.数学手册[M].北京：人民教育出版社，1979:608-610.

[3] 吴康，龙开奋.关于切比雪夫多项式的一些研究[J].中学数学研究，2006(3)：27-30.

[4] 凌明灿.第一类切比雪夫多项式方程的重根规律[J].五邑大学学报(自然科学版)，2013(5):13-15.

[5] 凌明灿.第二类切比雪夫型和式方程的研究[J].河南教育学院学报(自然科学版)，2012(12):11-13.

[6] 凌明灿.一类切比雪夫型方程组的通解[J].江苏师范大学学报(自然科学版)，2012(12)：46-49.

[7] 吴兰.关于四类切比雪夫多项式的研究[D].广州：华南师范大学，2014.

[8] 王中德.两类新的切比雪夫多项式[J].北京邮电学院学报(自然科学版)，1989(12)：46-54.

The General Solutions of the Third Kind of Chebyshev Equations

CAO Jiarui, WU Kang

(SchoolofMathematics,SouthChinaNormalUniversity,Guangzhou510631,China)

The third kind of Chebyshev equations with one unknown is defined. Get the general solutions of the two-order and higher-order equations by pairing each root of equation.

the third kind; Chebyshev equations; root; general solutions

2017-01-15

曹嘉芮(1994—)，女，福建长汀人，华南师范大学数学科学学院硕士研究生.

10.3969/j.issn.1007-0834.2017.01.005

O15

A

1007-0834(2017)01-0024-06