柔性压电发电机的发电性能分析

隋丽， 刘国华， 石庚辰， 王彭颖恺

(北京理工大学 机电动态控制重点实验室， 北京 100081)



柔性压电发电机的发电性能分析

隋丽， 刘国华， 石庚辰， 王彭颖恺

(北京理工大学 机电动态控制重点实验室， 北京 100081)

为提高微小型压电发电机的发电性能，设计了一种悬臂梁式的柔性风力发电机，通过实验与理论相结合的方法，分析了柔性悬臂梁振子的结构类型和结构尺寸对发电机输出电压的影响规律. 研究发现，合理选择压电振子的长、宽以及基底厚度，使压电振子在给定风速下产生共振将有助于提高发电机的发电能力. 在0～50 m/s的风速范围内，对不同结构尺寸的柔性压电发电机的发电能力进行了测试，实验结果表明：在压电振子能够发生共振的前提下，基底的厚度对发电性能的影响不大，而振子的长度及宽度对压电发电机的输出电压影响较大，且输出电压不随振子尺寸单调递增；在其他参数均为定值的前提下，压电振子的最优长度为40 mm，最优宽度为11.3 mm.

柔性梁；PVDF；发电机；涡激振动；共振

压电风力发电机是通过将风能转化为自身某个构件的振动能，进一步利用压电材料的正压电效应将振动能转化为电能的发电装置，具有结构简单、易于加工、成本低等优点. 目前，国内外已有部分研究人员开展了对柔性压电发电机的研究. Robbins W P等[1]研究了一种基于柔性压电材料的风能回收装置，为了提高发电机的发电效率，采取了一系列措施. 如：在自由端加入质量块，在出风口加入钝体，采用强耦合柔性压电材料，用准谐振整流器代替全波整流器. Tanaka Y 等[2]研究了基于压电薄膜的柔性发电装置. 该装置做了自由振动和受迫振动的相关实验，并提出PVDF压电薄膜应远离压电振子中间层. 在自由端施加2 cm挠度的激励时，通过收集电路，收集电容充电100 s所获得的电压为1.2 V. Mutsuda H等[3]在研究柔性风能回收装置时，发现振子的第2阶振动模态最有利于发电. 西北工业大学也研究了一种柔性风力压电发电机，它主要由柔性材料和PVDF压电薄膜组成，并给出了不同吹风方向的试验，即轴向和横向，该发电机的最大输出功率可达到60 μW，最高的能量密度为2 mW/cm3.

本文提出了一种柔性悬臂梁压电风力发电技术，利用军用场合中特殊的风能环境和压电材料的正压电效应，开展压电风力发电机的设计，研究具有体积小、柔性好、发电量高的新型发电机，为微小型电源的研究探索新的技术途径.

1 柔性压电发电机的模型与工作原理

1.1 柔性压电发电机的模型

压电材料主要分为无机压电材料、有机压电材料和复合压电材料[4]. 其中，以PVDF压电薄膜为代表的高分子有机压电材料是一种柔软的压电材料，可根据需要制成薄膜或电缆套管等形状，经极化处理后就显现出电压特性. 与传统的压电材料(如压电陶瓷)相比，PVDF柔韧性特别好、抗拉强度高，可以长时间工作于高强度的谐振环境[5]. 目前已在水声超声测量、压力传感器、引燃引爆等方面获得应用. 不足之处是它的压电应变常数偏低，使其在一些领域方面的应用受到限制.

带基底的柔性压电发电机主要由PVDF压电薄膜、304不锈钢基底、超薄双面胶带和导电双面胶带组成. 如图1所示为发电机的侧视图，发电机为三明治式结构，其中上层为PVDF压电薄膜，下层为304不锈钢金属基底，材料层之间使用约0.01 mm厚的超薄双面胶带粘接，发电机的固定端使用导电双面胶带将PVDF压电薄膜与基底粘接. 发电机的压电振子自由悬空部分使用超薄双面胶带不仅可以保证压电振子粘接牢固，同时也能确保压电振子具有较好的柔韧性. 压电振子的固定端使用导电双面胶带粘接主要作用是：① 使压电薄膜与金属基底之间电气导通；② 从压电振子上下表面引出电极时，可以直接把导线先粘到导电双面胶带上，然后再用强力电气绝缘胶布加固，这可以使导线与压电振子表面能够可靠连接导通.

1.2 发电原理

压电发电机主要有两种发电模式，即d31和d33模式， 本文利用的是压电材料的d31发电模式，与d33模式相比，d31模式的柔性悬臂梁风力发电机的谐振频率要低于d33模式，更容易在风场中产生颤振.

作为典型的流固耦合问题，柔性压电发电机在风中的振动是气动力、惯性力与弹性力的耦合结果，其本质在于风与结构之间的能量转化. 柔性压电发电机一端固定，另一端自由. 在轴向可变风载荷的作用下，柔性振子发生失稳振动. 柔性压电振子失稳振动时将发生变形，其内部产生拉应力或压应力. 由于压电薄膜具有压电效应，薄膜表面将有电荷产生，最终从压电振子固定端的引出电极对电荷进行收集储存.

2 柔性压电发电机的发电性能分析

2.1 涡激振动与锁定

从流体的角度来分析，任何非流线型物体，在一定恒定流速下都会在物体两侧交替地产生脱离结构表面的漩涡，使结构上下或左右两侧表面出现正负变化的压力和压力矩，称为涡激力. 在涡激力的作用下，结构开始发生涡激振动. 涡激振动在较低风速下就很容易出现，且带有自激性质，但振动的结构反过来会对涡脱形成某种反馈作用，使振幅受到限制，因此涡激振动是一种带有自激性质的风致限幅振动.

1878年斯特劳哈尔(V.Strouhal)在研究风琴的振动时最早发现弦线风鸣音频率与风速成正比，与弦线直径成反比的规律，并指出漩涡脱落频率可以用一个斯托罗哈数St描述：

(1)

式中：fv为漩涡脱落频率；v为风速；D为垂直于来流方向平面上的特征尺寸；St为斯托罗哈数.

当漩涡脱落频率接近或等于结构的某一阶固有频率时，流固耦合作用使得漩涡脱落频率在一个较大的风速区间内固定在结构的固有频率fn附近，漩涡脱落频率不再与式(1)相符，这时漩涡的脱落频率fv与结构振动频fn非常接近，换而言之，漩涡脱落频率被“锁定”在结构的固有频率附近[6].

2.2 柔性梁的振动分析

柔性梁与钝体尾流之间的流固耦合作用示意图如图2所示. 钝体尾流中周期性脱落的漩涡造成薄膜两边的压力差，驱使柔性梁振动. 根据悬臂梁的受力分析，可得悬臂梁受力的平衡方程以及力矩的平衡方程，经化简后得到梁的动力学控制方程，因此便可得到梁的各阶固有频率和振型函数，分别如式(2)和式(3)所示.

(2)

(3)

2.3 发电性能分析

如图2所示，柔性梁在振动的过程中发生变形，其两侧表面将产生拉应力或者压应力. 由于压电效应，压电薄膜的两侧表面产生电势差. 根据课题的实际情况，压电振子产生电荷与所受应力之间的表达式可简化为

(4)

式中：D3为梁z方向上的电位移；d31为压电常数；T1为梁x方向产生的应力.

由电荷与电位移的关系以及梁应力与应变的关系可得输出电压与梁振幅的关系式为

(5)

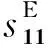
由式(5)可知，发电机的输出电压与压电振子的宽度、厚度、长度以及振幅y直接相关. 对于结构尺寸一定的压电振子，通过改变风速可使漩涡脱落频率fv也随之变化. 当fv与压电振子的某一阶固有频率fn相等或相近时，压电振子发生涡激共振，此时它的振幅最大，因此便可获得更大的输出电压. 由于锁定现象，随着风速继续增加，fv将在一个风速区间范围内保持不变，压电振子继续处于共振状态，发电机将保持高输出.

3 柔性压电发电机实验研究

3.1 实验装置

本文在研究过程中，先后使用了3种实验装置对压电振子的发电性能进行测试：自制低速风洞测试装置、F0-系列低速风洞和鼓风机风速加载实验系统. 其中鼓风机风速加载实验系统如图3所示，主要包括：风速范围为0～50 m/s的鼓风机、压电振子安装台、风速仪、稳压电源及示波器. 将样机引出电极端固定安装在所设计的夹具上，把引出的连线直接与示波器接连. 该实验系统风速加载范围较大，便于操作，其实验效果与商业化设备F0-系列低速风洞的测试结果相吻合. 考虑到实验周期、研究成本以及便利性等因素，本文最终选择鼓风机风速加载实验系统对压电振子的发电性能进行测试.

3.2 基底对压电振子发电性能的影响

由式(5)可知，在结构尺寸一定的情况下，压电振子的输出电压与振子的振幅有关，振幅越大，输出电压越高；压电振子的振动幅值除了与结构尺寸相关外，还与振子的刚度有关. 因此，希望制作出的振子刚度越小越好. 基于对振子的柔性需求，首先考虑使用无金属基底的PVDF压电薄膜制成压电振子，振子的总体尺寸为：50 mm×8 mm×0.03 mm. 对其进行吹风实验，使振子在风场中发生谐振，此时无金属基底压电振子的输出电压如图4所示. 由图4可知，尽管该振子产生谐振且振幅较高，但输出电压几乎为0.

由于无基底压电振子不具备发电能力，本文通过对各种基底材料的压电振子发电性能的实际测试，最终选用304不锈钢带作为压电薄膜的基底材料. 此时，压电振子的总体尺寸为：50 mm×8 mm×0.04 mm. 对其进行了吹风实验，使振子在风场中发生谐振，谐振时的输出电压如图5所示，平均幅值约为13.5 V.

3.3 风速对压电振子发电性能的影响

图6为有基底振子输出电压随风速的变化关系曲线，压电振子的结构尺寸如前文所述. 由图6可知，该结构尺寸的压电振子的临界风速为17.1 m/s，当风速小于等于临界风速时，发电机的输出电压几乎为0. 当风速大于17.1 m/s后，压电振子在风场中发生涡激共振，发电机的输出电压迅速增大；此后随着风速的继续增大，发电机的输出电压呈线性递增趋势，该实验结果与分析结果相吻合.

如前文所述，压电振子由PVDF压电薄膜与金属基底粘接而成. PVDF压电薄膜的厚度为0.03 mm，金属基底的厚度分别为0.01 mm和0.02 mm，振子的长度和宽度与前文相同. 这两种不同厚度的压电振子输出电压随风速的变化曲线如图7所示.

由图7可知，两种振子在发生谐振前，输出电压接近于0；0.01 mm厚金属基底的振子临界风速低于0.02 mm厚金属基底的压电振子；发生谐振后，厚金属基底的压电振子其输出电压要略高于薄金属基底压电振子的输出电压. 因此，在实际工程应用中，可根据给定的环境风速来选择金属基底的厚度，若环境风速较小，选择较薄的金属材料作为基底；若风速足够大，可选择厚金属材料作为基底，此外考虑到压电振子在高风速下的强度问题，选择厚基底比较合适.

3.4 结构尺寸对压电振子发电性能的影响

将0.01 mm厚的金属基底和0.03 mm厚的PVDF压电薄膜粘贴组合. 取宽度为8 mm，长度为20～90 mm不等的压电振子作为研究对象. 对不同长度的压电振子分别进行吹风实验，并且保证它们在0～50 m/s的风速范围内均发生谐振，图8为具有不同长度的压电振子发生谐振时输出电压的峰值曲线. 从图8中可以看出：压电振子的输出电压与其长度既不成正比，也不成反比，随着压电振子长度的逐渐增大，其输出电压先增大后减小，当L≈40 mm时，压电振子的输出电压峰值达到最大，约为15 V.

将0.03 mm厚的PVDF压电薄膜与0.01 mm厚的金属基底粘接组合形成压电振子，振子的长度取40 mm，制作宽度范围为4～14 mm的一组压电振子. 图9为不同宽度的压电振子，在谐振状态下输出电压的峰值信号. 由图9可以看出，当压电振子的宽度为11.3 mm时，输出电压曲线出现最高点，约为19 V.

从上述实验结果来看，压电振子的输出电压并不是随其长度及宽度的增大而增大，这与式(5)看似相互矛盾. 式(5)中，压电振子输出电荷的大小不仅与长度及宽度相关，还与它的振动幅值密切相连. 实验中发现，当压电振子的尺寸超过一定值时，它的谐振振幅将随之减小，此时振幅的减小对输出电压所起的负作用大于尺寸增加所贡献的正作用，因此压电振子的输出电压曲线出现回落.

4 结 论

由于现有实验条件所限，论文中所能提供的风速载荷范围为0～50 m/s. 为了能更好地研究柔性压电发电机的发电性能，制作了有金属基底、无金属基底以及具有不同结构参数的发电机样机，对这些发电机的发电性能进行了比较和分析. 实验结果显示，无基底的压电发电机几乎没有电压输出；有金属基底的压电发电机发生失稳共振时输出电压迅速增大，随着风速继续增加，发电机保持着高输出，这与理论分析结果相吻合；在发电机发生共振的前提下，振子的长度及宽度变化对发电机的性能影响较大，而金属基底的厚度对发电机的发电性能影响不大，当发电机的长度约为40 mm，宽度约为11.3 mm时，输出电压最大.

[1] Robbins W P， Marusic I. Wind-generated electrical energy using flexible piezoelectric materials[C]∥Proceedings of 2006 ASME International Mechanical Engineering Congress and Exposition. Chicago， New York: IMECE， 2006.

[2] Tanaka Y， Matsumura K， Mutsuda H. Study on flexible power generation device using piezoelectric film[J]. Energy and Power Engineering， 2012(6):353-360.

[3] Mutsuda H， Miyagi J， Doi Y， et al. Wind energy harvesting using flexible piezoelectric device[J]. Energy and Power Engineering， 2013(7):1047-1051.

[4] 林声和，叶至碧，王裕斌.压电陶瓷[M].北京：国防工业出版社，1980.

Lin Shenghe， Ye Zhibi， Wang Yubin. Piezoelectric ceramics [M]. Beijing: National Defense Industry Press， 1980. (in Chinese)

[5] 毛芹，王涛，郝鹏飞，等.基于PVDF压电片发电的特性研究[J].北京理工大学学报，2012(11):1140-1144.

Mao Qin， Wang Tao， Hao Pengfei， et al. Characteristics of power generation from PVDF piezoelectric film[J]. Transactions of Beijing Institute of Technology， 2012(11):1140-1144. (in Chinese)

[6] 杨瑞.桥梁主梁涡激振动理论预测模型研究[D].长沙：湖南大学，2011.

Yang Rui. Study on prediction model of vortex-induced vibration of bridge structures[D]. Changsha: Hunan University， 2011. (in Chinese)

(责任编辑：刘雨)

Power Performance Analysis of Flexible Piezoelectric Generator

SUI Li， LIU Guo-hua， SHI Geng-chen， WANG Peng-yingkai

(Science and Technology on Electromechanical Dynamic Control Laboratory，Beijing Institute of Technology， Beijing 100081， China)

In order to improve the performance of micro piezoelectric generator， a design of flexible cantilever-beam piezoelectric generator was proposed. The influence of the beam’s shapes and parameters on the output voltage of the piezoelectric generator， through theory and experiments was studied. Therefore a generator with appropriate structure parameters， such as length， width and substrate thickness will resonate easily on given wind speed， which helps to improve the power capacity of generator. Within a given wind speed range of 0 to 50 m/s， the power generating capacity of the flexible piezoelectric generator with different dimensions was researched. The experimental results imply that， the thickness of the substrate almost doesn’t affect the power performance with resonance， but the length and width of generator has a greater influence on the output voltage， and the output voltage is not monotone increasing with the length and the width. The optimum length of piezoelectric generator is 40 mm， and the width is 11.3 mm.

flexible beam; PVDF; generator; vortex-induced vibration; resonance

2014-07-03

国家部委预研基金资助项目(3030030331209)

隋丽(1978—)，女，博士，讲师，E-mail:bit_suili@bit.edu.cn.

TK 89

A

1001-0645(2016)01-0008-05

10.15918/j.tbit1001-0645.2016.01.002