FDM成型系统中模型摆放方向的优化方法

张　霞，张艳伟，姚鹏飞

（河海大学物联网工程学院，常州213022）

FDM成型系统中模型摆放方向的优化方法

张霞，张艳伟，姚鹏飞

（河海大学物联网工程学院，常州213022）

目前，对于单喷头的熔融沉积型成型系统而言，由于打印材料的单一性，后期的去支撑处理会对模型的成型质量产生极大的负面影响。在整个成型过程中，模型的摆放方向是待支撑面积大小的重要影响因素。在以上分析的基础上，为了改善模型的表面质量，提出了一种对模型的摆放方向进行优化处理的方案。建立了以支撑面积最小为优化目标函数的数学模型，利用遗传算法来求解，从而得出较优的模型摆放方向。采用C＋＋语言编写文中描述的算法，并选择一兔子三维模型进行测试，实验结果表明经过算法处理后的待支撑面积明显减少，验证了算法的可行性与有效性。

熔融沉积；减少支撑；模型摆放方向；优化处理；遗传算法；成型质量

1　引　言

熔融沉积成型系统（Fused Deposition Modeling，FDM）是将丝状热熔性材料在喷头内加热融化，通过一个带有微细喷嘴的喷头挤喷出来。热熔材料融化后从喷嘴喷出，沉积在制作平台或者前一层已经固化的材料上，当温度低于固化温度后便开始固化，通过材料的层层堆积最终形成制品。在3D打印技术中，FDM的机械结构最简单，设计也相对容易，制造成本、维护成本和材料成本也最低，是桌面级3D打印机中使用得最多的技术，其中模型的设计软件和打印机之间协作的标准文件格式是STL文件格式［1］。

对于FDM成型系统而言，最关键的依旧是成型质量及成型时间。影响成型质量的因素很多，例如切片层厚、扫描速度、打印温度以及打印支撑等［2］。目前，采用多喷头打印机进行打印时，在需要待支撑的部位采用水溶性材料进行打印，可以在保证质量的前提下，有效去除支撑，但是对于大部分的桌面级打印机来说，基本上都是单喷头打印机，采用一种材料进行打印，其中去支撑的后处理会严重破坏成型件的表面质量［3］，所以打印过程中希望待支撑的面积越小越好［4］。

为了避免以及减少支撑面积，操作者会自行对模型进行旋转选择合适的摆放方向。对于简单模型，用户的直觉判断会选择出合适的模型摆放方向；但是对于稍微复杂的模型，用户判断就会出现偏差。文中对模型的摆放方向进行优化处理，建立基于支撑面积的数学模型，利用遗传算法来确定合适的模型方向来减少支撑面，从而提高模型的成型质量［5］。

2　优化模型的建立

2.1模型的旋转变换

许多研究学者对模型的成型方向做了诸多研究，文中针对成型方向为Z轴正方向的打印机，让模型绕X／Y／Z轴分别进行旋转如图1所示，不改变模型的成型方向，而是优化模型的摆放方向。

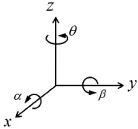
图1　模型的旋转方向

模型绕X／Y／Z轴分别进行旋转α、β、θ后，STL模型相应的点、三角面片都随着角度的变化做了改变，假设模型上一点坐标为（x0，y0，z0），根据旋转变换矩阵求出旋转后坐标的值如式（1）所示：

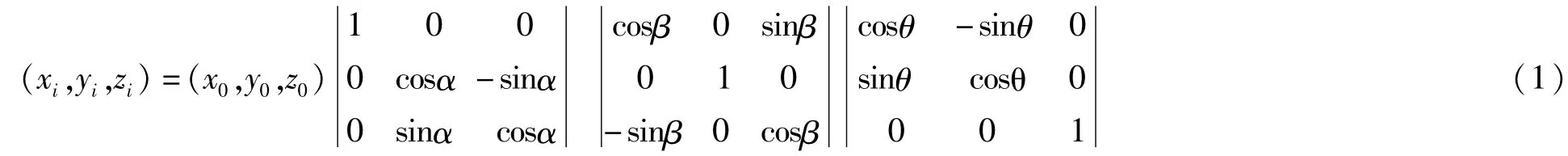
为了降低计算复杂度，并未采用STL模型的三角面片的面积作为评判标准，而是采用三角面片在平台（XY面）上的投影面积作为评判标准［6］。设第i个三角面片的坐标值分别为（xij，yij，zij），j=1，2，3，求得第i个三角面片的投影面积如式（2）所示：

2.2支撑面积的数学模型

加支撑的后处理对于成型件的表面质量具有严重影响［7］，为了提高成型质量，文中提出减少待支撑面的面积［8］。减少支撑面积应当使STL模型在成型方向（Z轴正方向）上法向量向下的水平面以及法向量向下且倾斜角度超过30°的面片尽可能的少，据此建立数学模型如式（3）所示：

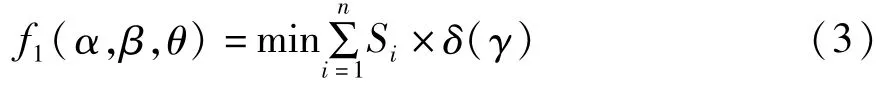
其中δ（γ）为一阈值函数，如式4所示，对于小倾斜角的悬垂面，依靠材料自身的粘结性在保证质量的前提下可以不用支撑进行打印，γ为三角面片法矢量n→与成型方向（Z轴正方向）的夹角，其中旋转后的单位法矢量n→也可以通过式（1）求得式（4）。

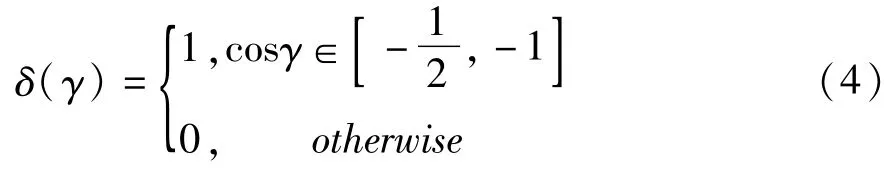
3　优化模型的求解

遗传算法是一类借鉴生物界自然选择和自然遗传机制的随机搜索算法，它是一个迭代过程，首先从随机产生的初始种群中开始搜索，然后将选择算子、交叉算子、变异算子作用于种族群体中，最后获得问题的全局最优解或近似最优解［9］。该算法结构相对简单，具有一定的实用价值，能够解决一些传统搜索方法难以解决的复杂系统的优化计算问题。

3.1适应度函数

适应度用于评价个体的优劣程度，适应度越大个体越好，反之适应度越小则个体越差。根据适应度大小对个体进行选择，以保证适应性能好的个体有更多的机会繁衍后代，使优良特性得以遗传。故适应度函数的选取对遗传算法的收敛速度以及是否能够寻求到最优解具有直接影响，许多场合下，目标函数与适应度函数是不完全一致的，在解决实际问题时，一般会将求最小值目标函数映射成求最大值形式并且函数值为正的适应度函数。文中将目标函数转换成如式（）所示的适应度函数：

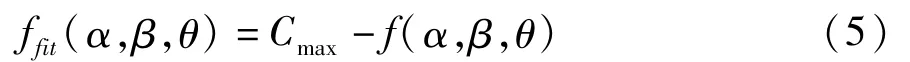
式（5）中Cmax是目标函数f（α，β，θ）的最大值。

3.2编码方式

为了改善遗传算法的计算复杂性、提高运算效率，对α，β，θ三个变量采用浮点数编码方式进行编码。三个变量的取值范围都为（0，2π），3个指定范围内的浮点数组成一个个体，随机产生此种个体作为初始种群。

3.3遗传算子设计

为了避免有效基因缺失，算法需要进行选择操作。文中采用轮盘赌选择法，可以确保适应度比平均适应度大的个体能够被遗传到下一代群体中，提高全局收敛性。

浮点型编码的基因突变过程一般是对原来的浮点数增加或者减少一个小随机数，这个小随机数称之为“步长”，为了使遗传算法的进化速度变快，保证最终结果能够精确收敛到全局最优解，采取动态改变步长的方法。其中遗传算子的参数设置如表1所示。

表1　遗传算子的参数设置

4　实验结果

在windows环境下，以Visual Studio 2010为开发平台，采用C＋＋编写了以上所述的优化模型摆放方向算法。如图2所示的兔子模型，模型的包围盒长、宽、高大小分别为：81.0mm、34.65mm、40.39mm，该STL模型由28736个三角面片组成，文中对这一兔子模型进行了测试。

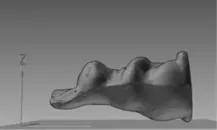
图2　优化前的模型

表2　优化前后参数变化

利用文中算法处理后，得出α=349.464、β= 95.7817、θ=278.16。如表2所示，未优化处理前模型的摆放如图2所示，优化前的模型待支撑面积为1652.85mm2，优化后模型的摆放方向如图3所示，待支撑面积为981.39mm2，支撑面积减少了40.62%，运用该优化算法得出模型较佳的摆放方向，验证了算法可靠性。

图3　优化后的模型

5　结束语

考虑到FDM成型技术中支撑对成型质量的影响，从减少支撑面积的角度出发来优化模型的摆放方向即改变模型的成型方向。相对于人为地来摆放模型而言，利用遗传算法寻求的最优摆放方向要精确许多，可以有效减少待支撑面积，大大减轻了支撑后处理对成型质量的影响，改善了成型件的表面质量。

［1］朱林泉，白培康，朱江淼.快速成型与快速制造技术［M］.北京：国防工业出版社，2003.Linquan Zhu，Kangpei Bai，Jiangmiao Zhu.Rapid Prototyping and Rapid Manufacturing Technology［M］.Beijing：National Defence Industry Press，2003.

［2］李金华，张建李，姚方萍，等.3D打印精度影响因素及翘曲分析［J］.制造业自动化，2014，36（11）：94－96.Jinhua Li，Jianli Zhang，Fangping Yao.Precision affecting factorsand warpage analysis of 3D printer［J］.Manufacturing Automation，2014，36（11）：94－96.

［3］张媛.熔融沉积快速成型精度及工艺研究［D］.辽宁：大连理工大学，2009.Yuan Zhang.Study on Process Precision of Fused Deposition Modeling［D］.LiaoNing：Dalian University of Technology，2009.

［4］Daekeon Ahn，Hochan Kim，Seokehee Lee.Fabrication direction optimizationtominimizepostmatchingin layeredmanufactering［J］.InternationalJournalof Machine Tools＆Manufacture，2007.

［5］K Thrimurthulu，Pulak M Pandey.Optimum part deposition orientation in fused deposition modeling［J］.International Journal of Machine Tools and Manufacture，2004.

［6］赵吉宾，何利英，刘伟军.快速成型制造中零件制作方向的优化研究［J］.计算机辅助设计与图形学学报，2006，18（3）：456－463.Jibin Zhao，Liying He，Weijun Liu.Optimization of Part－Buliding Orientation for Rapid Prototyping Manufacturing［J］.Journal of Computer－Aided Design＆Computer Graphics，2006，18（3）：456－463.

［7］刘厚才，储爱民.三维打印快速成型零件制作方向的优化研究［J］.工程图学学报，2009（3）：41－45.Houcai Liu，AimingChu.PartBulidingOrientation Optimization in Rapid Prototyping of Three Dimensional Printing［J］.Journal of Engineering Graphics，2009（3）：41－45.

［8］李淑娟，袁启龙，曹珊，等.复杂零件三维打印方向的建模与优化［J］.兵器材料科学与工程，2015，38（1）：58－62.Shujuan Li，Qilong Yuan，Shan Cao.Modeling and optimization of complex three－dimensional parts print direction［J］.Ordnance Material Science and Engineering，2015，38（1）：58－62.

［9］李华昌，谢淑兰，易忠盛.遗传算法的原理与应用［J］.矿治，2005，1（14）：87－90.Huachang Li，Shulan Xie，Zhongsheng Yi.Theroy and Application of Genetic Algorithm［J］.Mining and Metallurgy，2005，1（14）：87－90.

Optimization of Part Placement Direction In Fused Deposition Modeling System

Zhang Xia，Zhang Yanwei，Yao Pengfei
（College of Internet of Things Engineering，HoHai University，Changzhou 213022，China）

Currently，in terms of Fused Deposition Modeling system with a single nozzle，because of the unity of the printed material，processing after printing support will have a great negative impact on the molding quality.Throughout the molding process，placing direction of the model is an important factor for the size of bearing area.Based on the above analysis，in order to improve the surface quality of the model，we propose to optimize the placing direction of the model.The mathematical model is established to optimize the bearing area.Then the optimization of placing orientation is obtained by genetic algorithm.Using C＋＋language to write above algorithm and selecting a rabbit model as experimental subject，the result shows that the algorithm can obviously decrease bearing area，and verify the feasibility and effectiveness of the algorithm.

Fused Deposition Modeling；Reduce support；Model placement direction；Optimization；Genetic algorithm；Molding quality

10.3969／j.issn.1002－2279.2016.01.014

TP391.7；TH166

A

1002－2279（2016）01－0054－03

张霞（1990－），女，安徽省合肥市人，硕士研究生，主研方向：计算机图形学、三维打印。

2015－05－11