基于FPGA的DSTFT算法对FSK信号解调的改进
2016-11-21郭志阳孙向阳陈学英
郭志阳,孙向阳,陈学英
(电子科技大学 四川 成都 610054)
基于FPGA的DSTFT算法对FSK信号解调的改进
郭志阳,孙向阳,陈学英
(电子科技大学 四川 成都 610054)
针对运用离散短时傅里叶变换(DSTFT)算法实现解调2FSK信号时其存在的码元同步的问题。提出通过运用载波的功率谱估计和码元偏移的采样点数的关系,在系统通信开始的时候先实现精确的码元同步状态。由于在无线传输过程中存在噪声和频飘等现象,需要运用载波的功率谱估计跟踪码元同步状态,并且记录码元偏移的采样点数。当解调过程中再出现不同步状态的时候可以快速、精确的实现码元再次同步。并且通过仿真和在FPGA实现上表明该同步算法比其他同步算法误码率更低,并且在EM-WMD接收机上得到了应用。
2FSK;DSTFT;功率谱估计;同步算法;误码率
传统的对二进制移频键控(2FSK)调制信号的解调方法中例如差分检波法、过零检测法、包络检波法等都存在在低信噪比环境下,解调效果差并且误码率高的现象。随着数字解调技术在近几年得到迅速发展,出现了运用离散短时傅里叶变换、正交自延时和自适应递归数字滤波等方法,但是都存在码元起始同步和码元偏移点数跟踪的问题。文献[1]是根据定比值同步法来判断码元是否同步,该方法在低的信噪比下,稳定性比较差,误码率比较高;文献[7]是通过仿真谱图分段的设置阀值和当前幅度值比较来判断是否同步,再同步时仍然需要再次计算码元偏移点数,这将使系统消耗比较大并且将丢失一部分采样数据。
文中在DSTFT解调算法的基础上,运用两个载波功率谱估计的关系实现对码元偏移点数的记录和跟踪的同步新算法,能够在失步状态时候快速的进入同步状态,减少对系统消耗和数据的丢失,并应用于实际的EM-WMD接收机中,具有良好的解调效果。
1 总体设计
总体方案设计如图1所示。在接收天线接收到FSK信号后,需要通过模拟的滤波和放大提高弱信号的信噪比。ADC把采集的信号送给FPGA,在FPGA内部完成对FSK信号的滤波和DSTFT算法运算,在DSTFT算法的基础上完成:位同步计算、帧同步计算、位偏移监控、位偏差方向计算、再次的位同步的操作,能够在失步状态的时候快速的进入同步状态,减少误码率,提高系统性能。
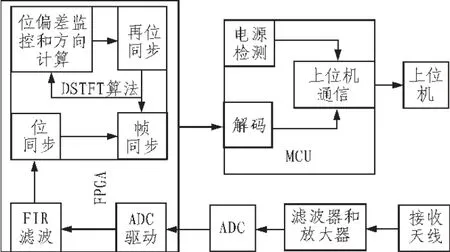
图1 系统总体结构图
解调过的数据通过并行通信传送给MCU,在MCU内部完成数据的解码,并且监控电路电源工作状态,把得到的数据通过串口发送到上位机。
2 DSTFT解调2FSK信号原理
典型的2FSK离散数字信号可表示为:
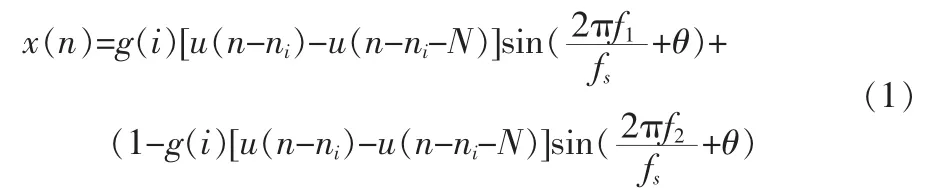
其中,g(i)代表第i个码元,N代表码元宽度,f1和f2分别是2个载波的频率,fs为采样频率,θ为相位。
DSTFT能够将时域信息转化到时频域进行分析[4],所以离散短时傅里叶变换适合对2FSK信号进行解调。DSTFT的定义如下表达式:
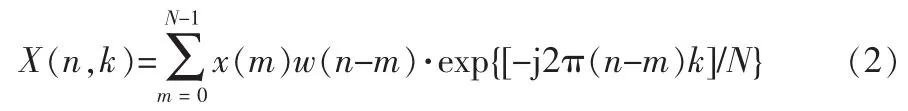
x(n)为输入信号序列,w(n)为移动窗函数,N为窗宽度。由此可见DSTFT是加移动窗的离散傅里叶变换。其可以看作是信号x(n)在n时刻附近的“局部频谱”,当n变化时,得到信号频率随时间n变化的规律。其将时域和频域组合在一起,反映了某一时间点附近的频率分布情况,因而可以提取频率分布信息。由公式(2)可以得到频率fi的频率点为ki=[Nfi/fs],其频率f点的幅度值为:
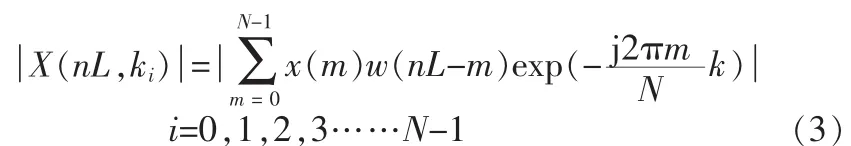
2FSK信号2个载波对应的频率点为kf1,kf2。由周期图法,可以得到其两个频率点处的功率谱估计,如下表达式。

随着窗函数的移动,频率点的功率谱估计在相应的变化,功率谱估计的比值(较大值除以较小值)称为阀值M,如下公式:
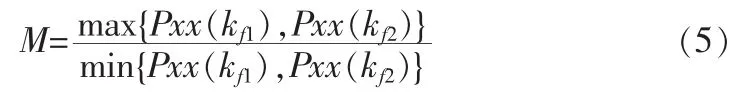
码元的判决方法如下:

式子中A1和A2为频率f1和f2所代表的码元。在上面的解调过程中要必须实现码元同步过程。由于起始的采样点是随机的,所以需要调整起始的采样点。所以好的同步算法将减少误码率的产生并且提升解调算法的性能。
3 码元精确同步算法
3.1同步算法原理
假设2FSK信号的两个载波频率的幅值相同,考虑信号的频谱结构将随着时间变化,通过窗函数取一段时间的信号,该段信号进行傅立叶变换后的频谱结构可以基本不变;然后通过移动窗函数改变截取时间段的位置,就可以得到频谱随着时间的变化而变化的二维曲线;通过分析两个频点的二维曲线,可以得到两个频点功率谱估计的比值的二维曲线,如图2所示不同偏移点下的f1/f2不同比值关系。

图2 不同阀值下的偏移点数
根据如图2所示,得到的两个频率点处的功率谱估计比值大小,进行量化后存储到FPGA的ROM里面,作为阀值M,并且每个阀值都对应相应的码元偏移点数。系统只有在检测到通信开始信号的时候才进行起始码元同步运算,此时候如果计算的M1>Ms,则表示已经检测到了开始信号。
3.2起始码元的精确同步算法
由公式(5)可知,当码元的偏移点说不同时将导致不同的阀值,通过与FPGA上存储的阀值M检索比较后得到其码元偏移点。由于在起始同步过后,要不断的跟踪和记录码元偏移点数,所以码元起始同步的时候采用精确同步。
1)移动窗函数(由于要实现精确同步,所以移动的偏移点数要很小以至于是1个采样点),运用DSTFT重新计算两个载波频率点处功率谱估计的比值M1,转到步骤2)。
2)判断是否满足停止移动窗函数条件:当M1>M的时候,结束窗函数的移动,起始同步过程才结束,否则回到步骤1),重新进行移位计算。
3.3码元跟踪再同步算法
考虑到信号同步后,受到信道、外部环境噪声、载波频点的取值不准确和移动窗函数导致的频谱泄漏等影响,导致接收机接收到一定的码元后,又将会出现失步的现象,需要重新进行同步操作。如果同步不准确将导致很高的误码率,严重的情况将解调不出2FSK信号。
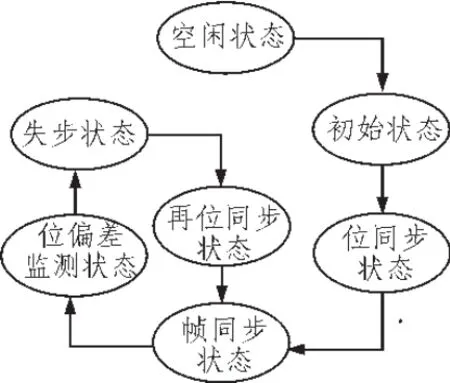
图3 DSTFT解调2FSK信号的状态变化
如图3给出了在DSTFT算法解调2FSK信号的过程中各种状态的变化流程,有效的完成了对2FSK解调过程中的监控。在失步状态后得到位偏移点的数值并且通过计算码元左右偏移方向实现再同步运算。
3.3.1码元偏移点数分析
由于信号由其实同步到失步是一个渐变的过程,由于起始同步运用精确同步的方法,则两个载波频率点处的功率谱估计的比值也是一个渐变过程。当出现较大的跨码元的情况是,得到的阀值将比较小。因此可以通过M1
3.3.2码元左、右偏移方向分析
通过检索比较计算的阀值在存储阀值中的位置,只能保证此时出现了较长的跨码元的情况。但是并不能确定码元偏移的方向,即不知道同步指针需要往左边偏移还是向右边偏移操作。需要进一步的计算和分析判断码元左、右偏移方向的条件。如图4所示,半圆为一个码元宽度,s是计算出的码元偏移点数。只有确定了码元偏移的方向才能进行偏移点数的移动,否则将导致同步错误。
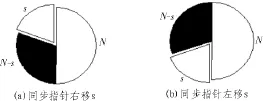
图4 码元左右偏移情况比较
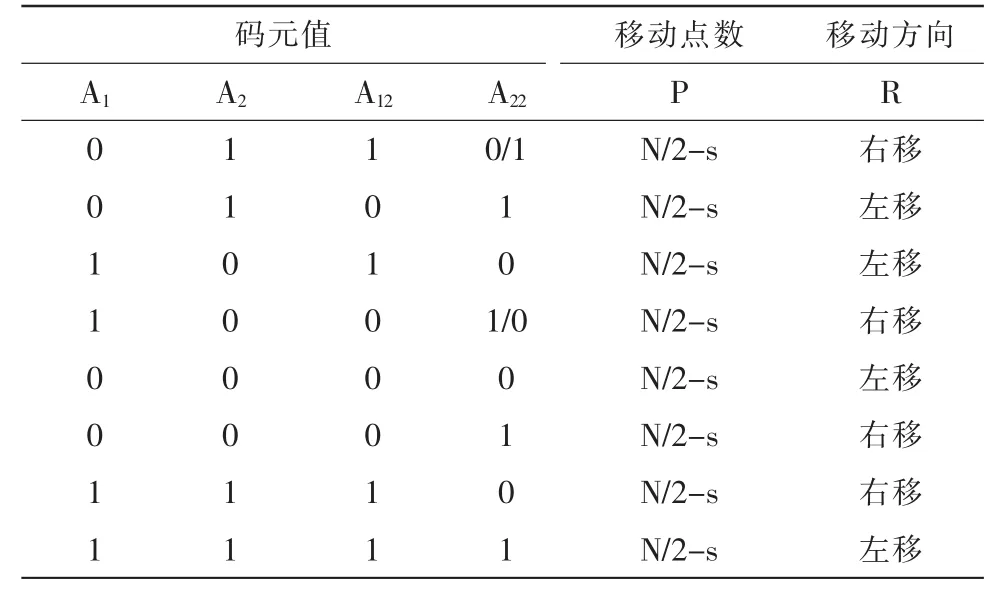
为了分析同步调整中是向左调整还是向右调整,其算法具体分析如下:假设通过DSTFT计算得到当前的码元为A2,之前计算的一个码元为A1,并且都要满足其Mi 短时傅立叶变换 (DSTFT)是把时域信号变换到频率信号,用Δt和Δf分别表示时间分辨率和频率分辨率;根据不确定性原理或者Heisenberg不等式,则它们的乘积必须满足不等式: 在码元判别和码元左右偏移方向判决时,由于L=N,则时间分辨率为Δt=T,此时频率分辨率为Δf=fs/N。由不确定原理或者Heisenberg不等式可得: 从上面公式看出,短时傅立叶变换(DSTFT)的时间分辨率和频率分辨率满足Heisenberg不等式。 表1 码元偏移点数和方向分析 文中在EM-WMD接收机上应用。两个载波频率设置上通过以下因素考虑: 1)2FSK信号的两个载波频率差值和基带信号波特率关系:Δf≥2·fT; 2)频率分辨率:fs/N; 3)工频信号和其谐波信号; 4)天线谐振频率; 基带信号的波特率fT为15.6 bit/s,一个码元的长度N为128,为了克服DSTFT计算频谱的时候出现频谱泄漏,窗函数选择Hamming窗,采样频率fs为2 000 Hz。通过以上数据得到两个载波频率分别为f1=164 Hz,f2=187 Hz。把图1计算得到的不同偏移点下的不同阀值存储到FPGA的ROM里,可以看出,以中心点为起点当码元偏移点说增加的时候,阀值将变的越来越小。通过在原始的2FSK信号上加了高斯白噪声,得到信噪比为-5 dB和幅度值为0.03 V的2FSK信号。用得到的2FSK信号数据在Modelsim对编写的Verilog代码程序进行综合仿真,保证程序逻辑正确性和可靠性,同时把仿真解调后的的数据导入MATLAB中绘制了如图5所示两个频点的谱估计的比值和同步效果。 图5 跟踪码元偏移点数保持同步状态 从图中可以看出通过计算偏移点数并且移动偏移点数后,码元进入同步状态,证明了偏移点数计算准确和码元跟踪记录再同步准确,使2FSK解调过程稳定满足设定的要求。 在实际测量中对如图6所示的2FSK信号进行ADC采样,把采样后的数据进行解调操作,能够完成解调、同步、码元偏移点跟踪和调整偏移点方向实现同步状态稳定等操作。 图6 幅度为20mv的2FSK信号波形 通过在上位机上能够看见解调后的基带信号数据。记录半小时的数据结果与发送数据对比发现,误码的数据非常少。在出现误码后能够在下一帧数据进入同步状态,实现了误码率在3%以下的2FSK信号解调操作。 在运用DSTFT算法解调2FSK信号的基础上,运用功率谱估计的方法来判断码元。并且在码元初始同步上运用精同步的方法,根据存储在FPGA[8]的ROM中阀值进行实时跟踪码元偏移点数。这样当出现跨码元长度比较大,要进行再同步的时候,只需要运用跟踪记录的偏移点数调整就可以。并且通过表1能够快速的锁定码元偏移方向,比其他算法具有更好的解调效果。其具有抗干扰能力强,误码率低,2FSK信号解调准确稳定等性能。通过在EM-WMD接收机上进行应用时,在信噪比很低的情况下能够实现误码率小于3%的效果。 [1]李伟光,李静,葛林东.一种基于DSTFT解调FSK信号的改进方法[J].现代电子技术,2003,26(6):26-28. [2]胡延平,李纲,王展,等.一种基于DSTFT解调2FSK信号的新方法[J].通信学报,2000,21(6):54-59. [3]冯小平,李红娟.用离散STFT实现FSK调制信号的数字解调方法[J].西安电子科技大学学报,2001,28(6):812-815. [4]殷晓中,于盛林.信号的时频分析理论与应用评述[J].现代电子技术,2006,29(21):118-120. [5]约翰逊,等.软件无线电[M].北京:机械工业出版社,2008: 21-27. [6]王楠,古瑞江,于红毅.一种新型的FSK解调系统设计[J],通信技术,2008,41(9):29-321. [7]金文光,张正宇,唐少华.2FSK信号DSTFT解调算法中的同步新方法[J].浙江大学学报,2011,45(6):1027-1031. [8]宋鹏,田乐.基于FPGA的时间同步精度的设计与实现[J].西安工程大学学报,2014(1):89-93. Improvement of FSK signal demodulation of DSTFT algorithm based on FPGA GUO Zhi-yang,SUN Xiang-yang,CHEN Xue-ying For using discrete short-time Fourier transform(DSTFT)algorithm to realize the demodulation 2FSK signal when the symbol synchronization problem of its existence.Put forward by the application of carrier wave power spectrum estimation and element migration of the relationship between the sampling points at the beginning of the system communication to realize accurate symbol synchronization state.Because in the process of wireless transmission phenomenon such as noise and frequency drift,need to use the carrier power spectrum estimation tracking symbol synchronization state,and record the element migration of sampling points.When demodulation can appear out of sync status again in the process of the realization of the fast and accurate symbol synchronization again.And through the simulation and shows that the synchronization algorithm on the FPGA implementationerrorrateislowerthanothersynchronizationalgorithm,anditsapplicationonthereceiverEM-WMD. 2FSK;DSTFT;power spectrum estimation;synchronization algorithm;error rate TN92 A 1674-6236(2016)21-0004-03 2015-11-06稿件编号:201511066 国家自然科学基金(61201281) 郭志阳(1990—),男,河南开封人,硕士研究生。研究方向:电路与系统和测井仪器研制。

4 试验结果分析


5 结 论
(University of Electronic Science and Technology,Chendu 610054,China)
