基于非线性有限元算法的高压电塔寿命预测

王伟

（广西电力职业技术学院 广西 南宁530000）

基于非线性有限元算法的高压电塔寿命预测

王伟

（广西电力职业技术学院 广西 南宁530000）

针对高压电塔在风载荷作用下的应力应变问题，提出一种基于非线性有限元的寿命预测算法。该算法根据高压电塔高柔低质的结构特点，并结合平均应力动态模拟电塔在风载荷作用下的疲劳寿命，最终达到对高压电塔的寿命预测。通过对220 kV高压电塔的实证模拟，结果显示：该算法的各阶自振周期模拟误差均小于5%，由Q420B型角钢材质构成的电塔主悬杆疲劳寿命仅为54.15年。该算法对工程设计具有一定的指导意义。

非线性有限元；高压电塔；风载荷；疲劳寿命

随着我国电力事业的快速发展，远程高压输电线路相继建设并投入运行，高压电塔故障的技术检测成为了电力部门遇到的难题[1-2]。电力资源通过高压电塔远程传输供给区域电能使用，当高压电塔发生倒塌或者倾斜等事故时，将导致大面积的区域断电以及通讯不正常[3-4]。以往电力部门采用直升机巡检，但是耗资较大[5]。因此，通过估计高压电塔的使用寿命可以有效降低电塔损坏带来的故障发生率[6]。

文中通过使用非线性有限元的方法对高压电塔进行分析，结合平均应力修正得到风载荷状态下的循环次数，从而动态模拟电塔在模拟电塔在风载荷用作下的应力应变，构造出高压电塔的有限元节点处的疲劳寿命。最后对Q420B型角钢和Q460T型钢组成的220 kV高压电塔的主悬杆、支护桩和塔头进行实证分析。

1　高压电塔非线性有限元建模计算原理

1.1非线性有限元理论

结构力学从本质上讲是非线性的，而非线性由可以分为两大类[7]：几何非线性和材料非线性。本研究对高压电塔采用材料非线性效应的应力应变，即工程应力描述材料非线性问题。由于高压电塔裸露在露天中，因此不可避免的受到强风的应力影响，从而边界条件随着高压电塔结构在强风速作用下引起非线性响应。假设非线性效应引起的位移分量是无限小量，假设高压电塔的单位刚度阵为K，质量阵为M，风载荷矢量为f，则非线性有限元离散化的节点可由如下代数方程组表示[8]：

其中，a为高压电塔对应位置的节点在风力影响下的位移向量。运用增量法求解代数方程组，将风载荷分为f0，f1，f2，…，在高压电塔响应的节点的位移也分为a0，a1，a2，…。假定第m个风载荷fm与高压电塔对应的位移am已知，只要每个风载荷增量Δfm足够小，则可以利用fm+1=fm+Δfm去求解，am+1=am+Δam。

1.2风载荷的模拟

由于高压电塔裸露在户外，不可避免的受到风的影响。因此，风载荷的模拟是必不可少的。风一般在时间和空间上表现为风速与风向上[9]，将风载荷的静力风和动力风作为高压电塔应力应变的共同作用结果。平均风速和脉动风速构成了高压电塔各节点所受到的瞬时风速，其中，平均风速为某时间段内空间某点各瞬时风速的平均值，脉动风速为某时刻空间某点瞬时风速与平均风速的差值[10]。计算高压电塔某时刻t的某点的瞬时风速为[11]：

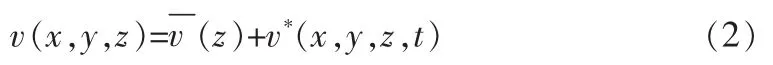
2　寿命预测与算法实现

2.1疲劳寿命

针对高压电塔的应力应变问题，采用上述非线性有限元建模的方式识别风载荷谱对高压电塔的各个节点回滞环数，从而得到风载荷应力幅下结构的循环次数。通过风载荷对高压电塔的疲劳分析，得到各方向的平均应力和应力幅，利用平均应力修正公式得到等效应力幅，并得出与高压电塔对应的节点的风载荷循环次数。对风载荷循环次数进行统计分析得到其中值，再利用S-N曲线模拟中值疲劳寿命。

考虑到风载荷的应力范围阀值问题，采用平均应力修正的方式来描述高压电塔的结构疲劳强度，平均应力影响因子λ为平均应力影响后计算得到的疲劳损伤度D0与不考虑平均应力影响计算得到的疲劳损伤度D的比值[13]，即

根据高压电塔的钢结构设计规范中关于构建和连接形式的分类，通过非线性有限元分析不同方向风载荷下的高压电塔结构的应力幅和循环次数，按照Miner疲劳累计理论，计算高压电塔的疲劳累计损伤[14]：

其中，k为风载荷块的数量，ni为i块风载荷应力幅作用下的实际循环次数，N为应力幅对应的高压电塔材料寿命。

2.2算法的求解程序实现

高压电塔在风载荷的作用下进行动态的非线性有限元分析，则可以利用Static Analysis改写非线性有限元分析中的函数domain Changed（）和analyze（），同时，通过定义solve Curren Step（）和analysis Model Changed（）函数来实现对算法过程中不同节点位移的步骤管理，最后，利用有限元分析风载荷的循环次数计算高压电塔的疲劳寿命。计算求解伪代码步骤见如下：

Step.1：Static Analysis::domain Changed（）//建 立 函 数domain Changed；

Step.2：Static Analysis::analyze//函 数 的 有 限 元 分 析analyze；

Step.3：Clsaa FESolution Algorithm//求解非线性有限元；

Step.4：Von Mieses Material::Compute Constiitutive Matrix//计算疲劳寿命.

3　实证分析

3.1高压电塔的有限元建模

本研究以220 kV输变电工程酒杯形输电塔为研究背景，电塔的呼高为32 m，塔全高为37 m，跟开8 m。塔身和横担的主材采用Q420B型角钢，其他主材和横隔采用Q460T型钢，塔底部按固结处理。对高压电塔采用非线性有限元离散化，产生655个节点和2 055个beam188梁单元，有限元模型如图1所示。

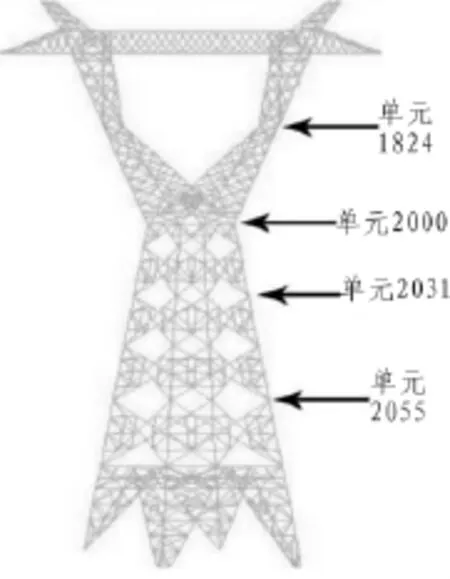
图1　酒杯形高压电塔的有限元建模

利用有限元分析软件中分块法对高压电压结构进行模态分析得到五阶振型，结合公式（5），根据我国电力行业对高压电塔实测研究，自振周期近似系数α=0.034。则五阶振型如表1所示。

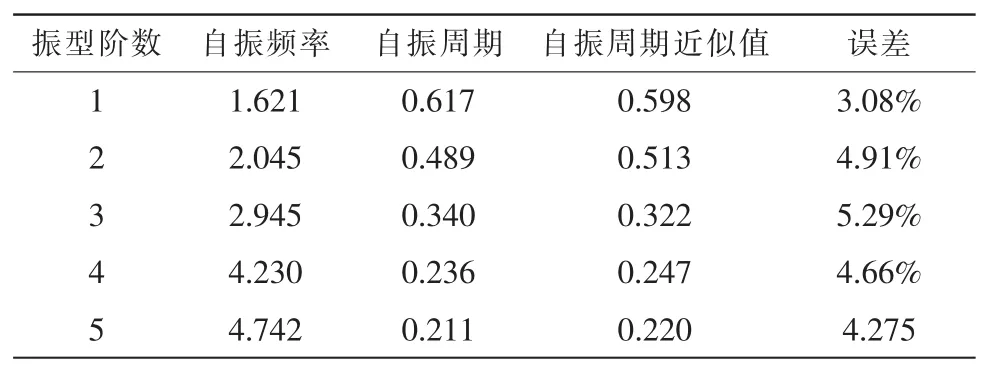
表1　高压电塔的五阶振型

由表1可见，非线性有限元建模算出的自振周期和结构自振周期误差均小于5%，在允许范围之内。说明了本研究利用的非线性有限元建模建立的高压电塔比较准确。

3.2风载荷模拟

如图1所示，由于主悬杆占据高压电塔主要长度，因此在模拟时需要进行一次模拟点的划分，即单元2031。利用Matlab程序分别对主悬杆（单元 2000-单元 2031-单元2000）、支护桩（单元1824-单元2000）和塔头（小于1824单元）4个模拟点进行风载荷模拟。通过线性自回归滤波器获得响应的参数：1）平均风速取31.25 m/s；2）桩基粗糙度系数取0.005；3）计算的时间步长取0.1 s；4）频率取0.01～10 Hz；5）计算振型阶数取3阶。3个模拟点的风载荷的功率谱如表2所示。由于高度愈高风速愈大，则功率谱愈大。由表2可见，高压电塔的塔头处所受到的功率谱在相同时刻处明显大于主悬杆处。

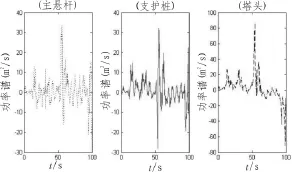
图2　模拟处风载荷的功率谱

3.3动力学分析

根据风载荷对高压电塔的应力应变的作用，将酒杯形电塔沿着竖向将32 m呼高等分为10段，采用非线性有限元时程分析法，以自重作用下的分析结果做为初始状态，分别计算每段的风载荷，然后平均分到高压电塔的节点上，最后将每个节点上的风载荷叠加得到电塔节点的风载荷的非线性动力模拟。

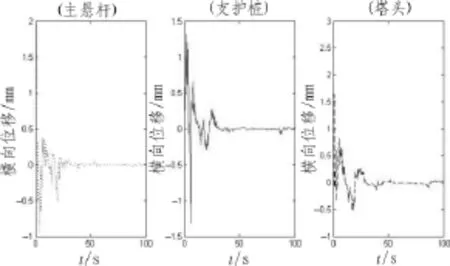
图3　模拟点处风载荷作用下的横向位移

由图3可得，在风载荷的应力应变作用下，高压电塔的横向最大位移出现在塔头处在2 s时刻，其最大位移值为3.0 mm。对应的计算beam188梁单元的应力均值与应力幅对应的风载荷循环次数，如表2所示。

表2　模拟点的风载荷循环次数

3.4寿命预测

采用幂函数的方式将S-N曲线对应的经验方程取对数整理后可得lgN=a+blgD，其中 a和 b为 Q420B型角钢和Q460T型钢常数（a=lg3.12e10，b=-lg3.02）[15-16]。对高压电塔的4个模拟单元点进行疲劳寿命分析，如表3所示。

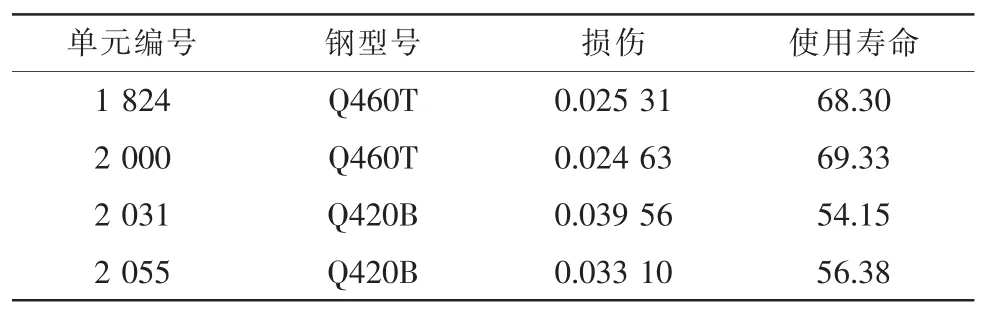
表3　高压电塔的疲劳寿命

由表3可见，主悬杆（单元2000-单元2031-单元2000）疲劳寿命的最小值为54.15年，而支护桩（单元1824-单元2000）和塔头（小于1824单元）的疲劳寿命最小值为68.30年。

4　结　论

本研究提出了求解高压电压使用寿命的非线性有限元算法，该算法动态模拟了高压电塔在风载荷作用下的应力应变问题，结合平均应力修正公式得到了高压电塔在有限元节点单元处的疲劳寿命。通过选用220 kV的高压电塔进行实证模拟，结果显示各阶自振周期模拟误差均小于5%，与此同时，电塔的疲劳寿命最小值出现在Q420B型角钢的主悬杆部位，其疲劳寿命为54.15年。该算法可以作为电力部门对高压电塔使用寿命的预测分析，对实践具有一定的意义。

[1]王越胜，陈星.高压电塔倾斜数据监控系统设计[J].杭州电子科技大学学报，2012，32（5）:247-249.

[2]陆竑.风光互补供电在输电线路视频监控系统的应用研究[J].节能，2014（6）:63-66.

[3]戴靠山，王健泽，毛日丰，等.一种风电塔架减振耗能装置的振动台试验研究[J].地震工程与工程振动，2014（1）: 868-872.

[4]郑松涛，汤文成，陈昀.SLP法在风电塔筒厂区总平面布置中的应用[J].工业工程与管理，2010，15（1）:116-120.

[5]杨勐，王玮，倪平浩，等.智能输电线路远程在线监测技术的相关研究进展及发展趋势[J].电气应用，2012（5）:20-24.

[6]张鹏林，曹力，刘九逍，等.风电塔筒在三种工况下的静动态研究[J].机械设计与制造，2013（10）:200-202.

[7]李志威，刘明军，刘腾澳.基于非线性有限元的可变形模型的变形方法[J].计算机应用.2013，33（3）:684-687.

[8]蔡勇，李光耀，王琥.GPU通用计算平台上中心差分格式显式有限元并行计算[J].计算机研究与发展，2013，50（2）:412-419.

[9]余娟，余明友，金建伟.风载荷作用下天线支撑杆稳定性分析[J].软件导刊，2013，12（4）:49-51.

[10]潘登，祁文军，宋长飞，等.基于VB设计的风能资源评估软件[J].计算机光盘软件与应用，2012（2）:177-178.

[11]刘章军，万勇，曾波.脉动风速过程模拟的正交展开-随机函数方法[J].振动与冲击，2014，33（8）:120-124.

[12]徐培福，肖从真，李建辉.高层建筑结构自振周期与结构高度关系及合理范围研究[J].土木工程学报，2014（2）:1-11.

[13]王文涛，上官文斌，段小成，等.基于线性疲劳累计损伤橡胶悬置疲劳寿命预测研究[J].机械工程学报，2012，48（10）:56-65.

[14]纪冬梅，轩福贞，涂善东，等.基于支持向量机的P91钢蠕变-疲劳寿命预测[J].压力容器，2011，28（10）:15-21.

[15]孙毅杰，李永祥，张杰新.Q420B高强度角钢工艺研究与控制[J].炼钢，2011，27（4）:29-32.

[16]黄伟兵.电力铁塔专用角钢性能研究[D].南昌：南昌大学，2011:42-44.

Predict the life of high-voltage tower based on the nonlinear finite element method

WANG Wei
（Guangxi Electric Power Vocational Technology College，Nanning 530000，China）

For high-voltage tower under wind stress and strain problems loads，made life prediction algorithm based on nonlinear finite element.The algorithm based on the structural characteristics of high-voltage tower soft low-quality，and combined with the average stress dynamic simulation electrical tower under wind loads of the fatigue life.It ultimately achieved the high-voltage tower life prediction.Finally，220KV high-voltage tower empirical simulation results show that:each step of the algorithm natural cycle simulation error is less than 5%，the main angle from the Q420P type material constituting the suspension rod fatigue life of only 54.15 years.This algorithm has some guiding significance for engineering design.

nonlinear finite element；high-voltage tower；wind load；fatigue life

TN06

A

1674－6236（2016）21-0018-03

2016-03-13稿件编号：201603153

国家自然科学基金项目（50767001）

王 伟（1982—），男，山东威海人，工程师。研究方向：高压输电线路施工检修。