基于概率排序算法的企业排班系统研究

张昊，王飞

（河海大学 商学院，江苏 南京 211100）

基于概率排序算法的企业排班系统研究

张昊，王飞

（河海大学 商学院，江苏 南京 211100）

针对企业现有岗位和员工资源限制下，为实现所有岗位均有员工在职的目标，考虑员工空闲或者忙碌的时间因素、员工数量和岗位数量的大小关系以及每个员工对应的岗位数量对排班系统的影响，利用随机概率生成员工忙闲时间分布空闲概率，并结合排序算法对员工岗位配对进行排序。实证仿真结果显示：算法进行100次循环稳定性较高；当员工数量和岗位数量均为10时，员工空闲概率为0.8；当员工数大于岗位数时，员工空闲概率为0.9；而员工人数增加到21人时，空余岗位数量为0的概率接近1。

概率分布；排序算法；差异排班；无差异排班

在排班系统中，公平、合理的排班方法对于调动工作人员的工作积极性、提高工作效率都具有重要的意义[1]。企业的排班问题是公司正常运转面临的重要问题之一，人力成本在企业的日常营运过程中占了一部分重要的支出[2]。企业排班问题可分为两大问题[3]：一是员工数恰好等于工作岗位数，即无差异排班；二是员工数不等于工作岗位数，即差异排班。而排班系统作为企业资源配置的关键节点，必将会发挥更大的作用[4]。对于小企业来说更是如此，员工需要花费大量的工时用于工作岗位，这对排班系统提出了更高的要求[5]。排班系统安排能适应员工时间和岗位变化的一种灵活性组织管理[6]，企业进度的规划、员工人力资源以及员工与岗位之间的匹配是影响排班系统的关键因素[7]。因此，合理的排班系统是企业顺利运转的重要保证，也是保证员工集中时间提高工作效率的重要基础。

本研究以员工数量和岗位数量为排班系统的依据，以所有岗位均有员工在职为目标，结合员工空闲或者忙碌的时间因素、员工数量和岗位数量的大小关系以及每个员工对应的岗位数量对排班系统的影响，利用随机概率生成员工忙闲时间分布空闲概率，并结合排序算法对员工岗位配对进行排序。

1　模型的建立

1.1问题描述

企业的岗位排班系统是一个重要战术决策问题[8]，在制定排班指派的中长期计划时，每个月岗位的人员安排可以根据企业人力资源管理制度明确得出，但是由于管理层员工的随机性，在未来每个月的员工的忙闲情况是不确定的[9]。假设每位员工每个月的工时分布独立且服从同一分布，企业需要根据员工及其忙闲分布、岗位用工时数等安排每个月供需要在岗的对应排班的数量，使得整个排班系统中没有员工在岗工时数量最少，所有岗位均有员工的概率最大[10]。在上述情况下，影响排班系统的因素主要包含两个方面：员工数量和岗位数量的大小比例关系、对应岗位的工时，分别研究这两个因素对于排班系统的影响，以所有岗位均有员工在职的概率最大为目标，在此基础上制定出调整排班指派关系或员工增减的长期决策。

1.2条件假设

本研究针对企业每月进行一次排班的分析[11]，因此假设如下：1）员工工作能力无差异；2）每个员工在职的机会成本相同；3）只考虑岗位数量，不考虑相同岗位存在相同的工作绩效担当；4）排班之前不确定每个员工忙碌与空闲的情况。

在排班系统研究中，员工数量和岗位数量的大小关系影响排班系统的设置，研究对应岗位数量对排班系统的影响时，还需要假设在该企业中员工的数量和岗位的数量相等。由于排班系统中，员工的能力和工种的差异会导致对应岗位数量存在差异。因此，不考虑这种差异，则假设所有员工对应的岗位数量相同，不存在某些员工对应同一岗位而某些员工同时对应两个岗位的情况。

2　概率排序算法

2.1概率分布

基于以上4点条件假设，只知道所有员工空闲和忙碌的时间服从0-1的概率分布，其中，0代该表员工可以从事该项岗位，概率为α；1代表该员工无法从事该项岗位的机会成本非常大，概率为1-α。因此，对于员工的忙碌与空闲时间分布概率如表1所示。

表1　员工时间分布概率表

在每位员工对应一个岗位的情况下，由于员工空闲概率为α，忙绿概率为1-α，因此，对应岗位有员工在职的概率为α，没有员工在职的概率为1-α，当员工数量和岗位数量为m时，没有员工在职的岗位数的概率可以表示为[12]：

在每个员工对应两个岗位的情况，只有岗位对应的两个员工都处于忙碌状态时才会出现该岗位为空余岗位，相对于对应岗位数为1的情况，空余岗位数为0的概率会有所降低，由于对应岗位数大于2时，直接解析计算概率会比较复杂[13]，因此，利用随机概率算法对员工的时间分布进行分析。

随机概率算法以每个员工空闲概率为α的概率随机生成100次所有员工的时间分布值，根据该分布计算不同课程对应状态下空闲岗位的概率值，根据员工空闲或者忙碌的状态派段空闲岗位数量，计算得到100个空余岗位数量，同时，得到每个空余岗位在100次计算中的比例得到空余岗位数对应的概率。

2.2排序算法

将待排序的员工空闲概率与岗位数量分别存储在连续的顺序物理空间A={a1，a2，…，an}和B={b1，b2，…，bm}中，从两头开始排序[14]，每趟定位2个元素，即找出当前待排序员工空闲概率的最大值amax和岗位数的最小值bmin，将最大值移动到末尾，最小值移动到首位，重复上一趟工作，这样每趟缩小2个元素的待排范围、并定位，知道范围缩小到剩余1或者0个元素。当n为偶数时最终以0个待排数量中值，当n为奇数时最终以1个待排数量终止[15]。算法步骤如下：

Step.1：置趟数计数器j=0，找出员工数组中最大值的位序下标和岗位数组中最小值，并记录在max和min中；Step.2：如果max=j，则完成以下运算

Step.4：趟数计数器j增1，即j=j+1；

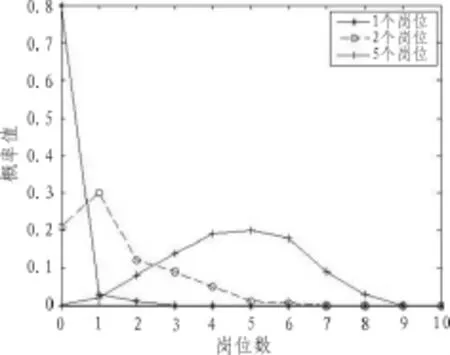
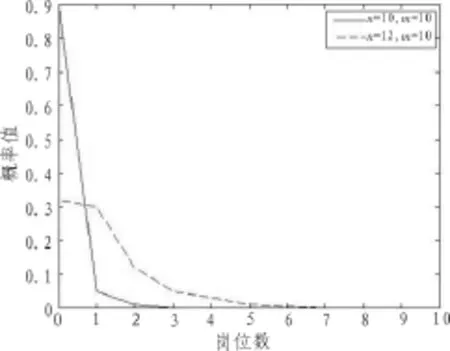
Step.5：如果j

2.3随机概率排序算法

基于员工空闲和忙碌的时间服从0-1的概率分布和排序算法，本研究将两个算法进行整合使用，具体算法流程如图1所示。

图1　随机概率排序算法

3　实证检验

3.1算法分析

从算法描述中不难发现，对于具有m个岗位的序列完成排序，一共需要进行m/2趟，每趟完成元素对比次数为次m-2j-1（j为趟次，0≤j＜m/2），即总对比次数为[16]：

当寻找到第j趟中员工空闲概率的最大值和岗位数最小值后，需要把最大值元素移动到m-j-1处，把最小值元素移动到j处，每趟的移动赋值运算最多8次，所以排序总移动赋值次数最多为4m次[17]，该算法的总时间复杂度为（m2+m）/4。当数据序列为正序时，每趟移动元素的次数为0，算法的总时间复杂度为m2/4。当数据序列为逆序时，每趟移动元素的次数最多4m次，则该算法关于循环次数的稳定性如图2所示。其中，趟数计数器从0到100循环过程中，算法逐渐趋于稳定。

图2　算法的稳定性

3.2无差异排班

当员工数量和岗位数量相等m=n=10，员工空闲概率为0.8，利用上述算法计算不同岗位对应关系下空闲岗位数量对应的概率大小得到结果如图3所示。

图3　岗位数量对空余岗位数量概率

由图3可以看出，当空余岗位数量较小时，对应岗位数越多空余岗位对应的概率值越大：在极端情况下，当空余岗位数为0，每个员工对应5个岗位可以使得概率接近1，即几乎能够保证所有岗位均有员工在职；对应岗位数为1时，空余岗位为0的概率只有0.028，几乎不能保证所有岗位均有员工在职；对应岗位数为2时，空余岗位是0的概率为0.47，只有约一般的可能性保证所有岗位均有员工在职。当对应岗位数量从1开始且以1的速率累计增加时，空余岗位数量的平均值下降的速度远远大于对应岗位数量增加的速度，由5.99下降到1.79，继而下降为0.51。

根据以上计算，增加对应岗位数量可以增加空余岗位的概率为0，然而，由于员工的工种和精力相对有限，过多增加对应岗位数量会加大员工压力进而影响工作质量和进度。

同时，员工空闲概率为0.8，每个员工对应5个岗位几乎就能保证所有岗位均由员工完成正常运转的概率为1，过多的增加对应岗位数并没有必要。

3.3差异排班

由于考虑员工数量与岗位数量之间的差异性，假设员工数量多于岗位数量为2，即对于某个岗位对应的2名员工都处于忙绿状态时才会出现该岗位空余的情况。因此，一个剩余空闲员工只对其中一个空闲岗位进行补充，只有剩余员工均处于忙碌状态时才会出现该岗位最后成为空闲岗位，在员工数为n=8，n=10，岗位数为m=10，员工空闲概率为0.9的情况下，得到空闲岗位概率如图4所示。

图4　员工数大于岗位数时空闲岗位概率图

由图可以看出在同一对应关系下，员工数量多余岗位数量会明显降低空余岗位为0的概率，因此在不改变每位员工对应岗位的情况下适当增加员工可以减少空余岗位的产生。员工的增加会增加排班系统的成本，考虑员工的累计增加对排班系统的影响，在对应岗位数为2和岗位数为11的情况下改变员工的数量，得到的结果如表2所示。

表2　员工数量对应空余岗位的影响

员工数量持续增加，空余岗位数为0的概率不断增加，空余岗位的平均数不断减少，当员工人数增加到21人时，空余岗位数量为0的概率接近1，可以满足所有岗位均有员工在岗的目标。在岗位数量固定的情况下增加员工可以减少岗位，保证企业正常运转的顺利实现，而员工增加的数量需要比较增加员工的成本和出现空余岗位产生的损失，寻求两个成本之间的平衡点保证两者之和最小，实现排班系统所有岗位均有员工在岗以及成本最小的目标。由于不同对应岗位数也会影响空余岗位，增加员工数量的同时也可以考虑改变每个员工的对应岗位数，此时排班系统最优的策略是实现员工的成本最小。

4　结　论

文中研究了以企业员工数量和岗位数量为系统的排班问题优化，在综合考虑员工的忙碌与空闲时间的概率分布的情况下，利用了随机概率生成空闲岗位数量，同时，利用排序算法对随机生成的空闲岗位与空闲员工进行匹配，从而提高企业员工的工作效率。在设计算法时利用概率分布的基本思想，对其稍作改进后使之适用于企业排班系统的求解，并通过算例证明了该算法同时适用于差异排班和无差异排班系统。参考文献：

[1]林红，饶云波，李勇.遗传算法在乘务员排班系统中的应用[J].计算机技术与发展，2007，17（1）:199-202.

[2]刘欣.大型集团企业人力资源管理信息化建设[J].电力信息化，2011，09（5）:47-50.

[3]章坚民，吴鑫淼，陈耀军，等.供电公司移动作业排班调度优化模型及算法[J].电力系统自动化，2013，37（14）:81-88.

[4]张立，夏孝洁，忻凌，等.护理实习生排班系统的研发与应用[J].电脑知识与技术，2015（8）:21-27.

[5]刘晓云.我国中小企业人力资源管理问题研究[J].经济体制改革，2011（5）:112-115.

[6]陈璐，陈湘玉，八卷直一.电子排班系统的开发及应用[J].中华护理杂志，2012，47（12）:1118-1119.

[7]梁剑波，柴群.遗传算法在多类型的车辆人员排班系统中的应用与研究[J].电脑知识与技术，2014（12）:8266-8267.

[8]夏正洪，潘卫军.呼叫中心智能排班系统关键技术[J].计算机工程与设计，2015（5）:1332-1336.

[9]曹清越.基于Web的排班管理系统设计思路[J].信息与电脑：理论版，2013（1）:121-122.

[10]程元军，罗利.基于排队论和整数规划的银行柜员弹性排班模型[J].管理学报，2010，7（10）:1558-1565.

[11]苏强，赵飞.多技能呼叫中心排班算法研究[J].系统工程理论与实践，2015（1）:239-246.

[12]蓝伯雄，张米.考虑延误因素的机组排班模型研究[J].中国管理科学，2015（12）:33-41.

[13]郑伟，王朝坤，刘璋，等.一种基于随机游走模型的多标签分类算法[J].计算机学报，2010，33（8）:1418-1426.

[14]刘凯鹏，方滨兴.一种基于社会性标注的网页排序算法[J].计算机学报，2010，33（6）:1014-1023.

[15]石海鹤，薛锦云.基于PAR的排序算法自动生成研究[J].软件学报，2012，23（9）:2248-2260.

[16]淦艳，杨有.5种排序算法的性能分析[J].重庆文理学院学报：自然科学版，2010，29（3）:45-50.

[17]卢敏，黄亚楼，谢茂强，等.代价敏感的列表排序算法[J].计算机研究与发展，2012，49（8）:1738-1746

Enterprise scheduling system based on probability sorting algorithm

ZHANG Hao，WANG Fei
（School of Business，Hohai University，Nanjing 211100，China）

Under existing jobs and enterprise staff resource constraints，to achieve the goal of serving all posts are staff employees idle or busy considering the time factor，the number of employees and the number of jobs as well as the relationship between the size of each employee corresponding to the number of jobs affect scheduling system，using a random probability generating employees busy idle time distribution probability，combined with sorting algorithm to sort the pairing of staff positions.Empirical Simulation results show that:the algorithm 100 times higher cycle stability；when the number of employees and the number of jobs are 10 employees idle probability is 0.8；when the number of employees is greater than the number of jobs，people are free probability is 0.9；and increase the number of employees to 21，the number of vacant posts 0 probability close to 1.

probability distribution；sorting algorithm；difference scheduling；no difference scheduling

TN-9

A

1674－6236（2016）21-0007-04

2016-03-20稿件编号：201603263

国家自然科学基金项目（71372166）；江苏高校哲学社会科学研究重点项目（2010ZDIXM004）

张 昊（1992—），男，吉林大安人，硕士研究生。研究方向：财务管理。