油套管螺纹端面密封微观接触性能数值模拟

蔄靖宇, 黄龙文, 安 琦

(1.华东理工大学机械与动力工程学院,上海 200237; 2.上海电力学院数理学院,上海 200090)



油套管螺纹端面密封微观接触性能数值模拟

蔄靖宇1,2, 黄龙文1, 安 琦1

(1.华东理工大学机械与动力工程学院,上海 200237; 2.上海电力学院数理学院,上海 200090)

油套管接头在油气田工业中已得到广泛使用,其密封性能对油气井生产安全与环境将产生重要影响。以上扣拧紧时的螺纹接头为研究对象,在弹性范围内构建了锥螺纹接头端部密封面上挤压力的计算方法。利用粗糙密封表面微观接触分析方法,以某一具体的API圆螺纹接头为例数值模拟了拧紧力矩(圈数)、表面粗糙度和初始密封面间隙对端面密封性能的影响规律,获得了相应的变化曲线,并对这些曲线进行了分析。

油套管螺纹接头; 端面密封; 接触压力; 粗糙表面; 数值模拟

石油工业中的油套管接头多采用带有一定锥度的圆锥管螺纹联接(如API螺纹接头),这种联接具有成本低、易装配、互换性强、技术成熟等优点,因而得到广泛应用。圆锥管螺纹接头拧紧后,在其内、外螺纹之间都会产生一定的配合间隙,为空间螺旋状,从而易于形成泄漏通道。在实际应用中,圆锥管螺纹的密封一般通过两种方法：一是填充螺纹脂,但密封脂易于挥发变质,可靠性不高;二是通过结构设计,在管体外螺纹螺尾端与接箍端面设置密封台阶面,通过相互挤压接触而形成密封面。

要对圆锥管螺纹端面接触密封的性能进行研究,首先要研究圆锥管螺纹拧紧过程的力学性能。Maduschka[1]和Sopwith[2]首先提出了螺纹联接的解析模型,并对圆柱螺纹拧紧时的载荷分布进行了分析计算。结果表明,由上扣扭矩产生的轴向载荷一半以上是由最先啮合的前几圈螺纹承担的。Bruschelli等[3]通过对Sopwith模型修正建立了锥螺纹解析模型,针对锥螺纹接头给出单圈螺纹牙载荷分布的计算方法。Wang等[4]利用修正的弹簧模型研究了螺纹接头,通过简化的二阶微分方程计算分析了轴向载荷分布。高连新等[5]以单圈螺纹牙为研究对象,利用积分方法得到了螺纹联接轴向拉伸时的载荷分布计算公式,并指出分段变螺距可以明显改善套管螺纹的受力分布特性。陈守俊等[6-7]利用厚壁圆筒理论和微分方法建立了锥螺纹拧紧时单圈螺纹牙径向载荷分布与拧紧扭矩的计算方法。目前的研究表明,螺纹接头在工作过程中,每圈螺纹牙上的受力分布是很不均匀的,轴向拉伸时大部分载荷主要集中在接头的两端,上扣拧紧时大部分载荷主要集中在最先啮合的前几圈。这些研究大都是在没有考虑油套管密封端面的力学作用下进行的。

圆锥管螺纹的端面密封属于金属接触密封,其密封原理在于:在受到压力作用下,微观接触微凸体发生变形,当变形达到一定程度,通过紧密贴合阻止流体通过,实现密封效果。金属接触密封的微观形貌变化及应力分布规律十分复杂,这种变形和应力分布的性能是决定其密封性能的关键。

申昭熙等[8-9]对特殊螺纹接头进行了研究,通过有限元分析,得到螺纹接头有关结构参数对密封面接触压力的影响,得出压力分布的规律。周鑫等[10]对球面密封结构进行了研究,通过有限元分析,研究了其接触面受力分布,发现密封面接触压力在一定范围内增长会改进密封性能。Murtagian等[11]以螺纹管接头为对象,通过试验的方法研究了其密封性能,发现金属接触静密封中接触压力和接触长度的变化对密封性能的影响规律。Jun Takano等[12]对特殊螺纹接头金属密封结构进行了研究,发现随接触压力的增大,泄漏面积会逐渐变小,接触面积越大，泄漏路径越长,密封性能就会更好。Marie等[13]对拧紧力作用下的金属接触密封进行了研究,给出有效测量流体泄漏率的试验装置和计算方法。从目前的研究情况看,大多采用有限元分析方法或试验方法研究密封性能及其参数,鲜见进行深入的理论建模研究。

本文以文献[6，14]所建立的油套管接头拧紧时的计算模型为基础,考虑密封端面的力学作用,建立了一种能够在弹性范围内计算油套管接头端部密封面上挤压力的力学模型。利用自相关函数和均方根粗糙度通过计算机模拟方法获得了油套管锥螺纹密封接触端面的微观三维形貌,对粗糙密封表面进行了微观接触分析,建立了油套管锥螺纹拧紧过程密封接触面上的相互趋近量、接触面积和最大接触压力的计算方法,在此基础上数值模拟了拧紧力矩(圈数)、表面粗糙度和初始密封面间隙等因素对端面密封性能的影响规律。

1 密封面压紧力计算方法

在对油套管锥螺纹进行力学分析时,采用的假设与文献[6]一致,即:螺纹变形在弹性范围内;忽略螺旋升角的影响;简化成等腰三角形螺纹;不考虑螺纹牙齿弯曲变形;不考虑扭转变形。考虑密封端面的力学作用,经过简化后,管体与接箍拧紧到手紧位置时(未发生径向过盈)的联接示意图如图1所示,其中δ0为手紧后两密封端面的初始间隙。

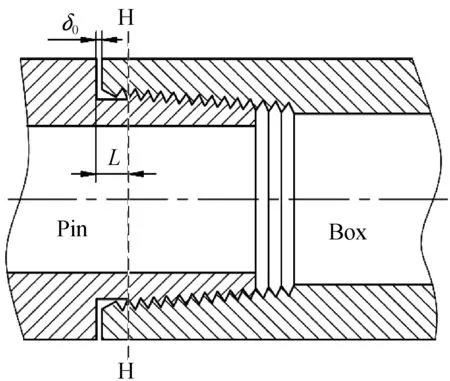
图1 管体与接箍手紧时的联接示意图Fig.1 Simplified schematic of the conical threaded connection in the hand-tight position

从手紧位置起,在上扣扭矩T的作用下旋进N圈后,管体外螺纹螺尾端的台阶面与接箍端面相互接触压紧而形成密封面,机紧时管体与接箍的联接状态如图2所示。其中δr为内、外螺纹径向过盈量。由于螺纹锥度的影响,管体与接箍的螺纹牙发生径向过盈配合,使得管体发生径向压缩,接箍发生径向扩张。同时,螺纹牙的径向过盈配合促使管体和接箍在螺纹牙面上产生一个相互挤压力。

图3所示为接头拧紧后管体与接箍的受力情况,密封端面上产生压紧力,管体沿轴向受拉力W′的作用,接箍沿轴向受压力W的作用,发生啮合的管体外螺纹与接箍内螺纹的螺纹牙左右两侧因径向过盈而受到法向接触压力pL(zi)和pR(zi)作用。密封端面上所受的压紧力将直接影响到密封效果,为此应建立求取该压紧力的计算模型。

图2 机紧时管体与接箍的联接示意图Fig.2 Connection of the pin and box in the power-tight position

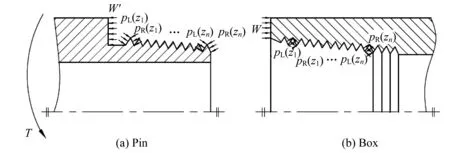
图3 机紧时管体与接箍的受力情况Fig.3 Load conditions for the pin and box in the power-tight position 由文献[6]可计算单圈螺纹单侧齿面上的拧紧的力矩Ts,其值为

(1)

式中:x1、x2为螺纹牙轴向有效接触长度积分上、下限;α为螺纹牙型角；Dit为发生接触的管体第i圈外螺纹牙顶面的直径;P为螺距;μ为摩擦因数。管体与接箍发生径向过盈配合后,则任意一圈螺纹单侧齿面上的接触压力p(zi)为

(2)

式中:E为管体与接箍(假设材料相同)的弹性模量;D0为接箍的外径;d为管体的内孔直径。当螺纹接头拧紧N圈时,螺纹径向过盈量δr为

(3)

其中t为螺纹锥度。由于端面挤压力的影响,螺纹牙两侧的径向过盈量并不相同。δr进行修正可得到螺纹牙两侧的实际径向过盈量,将其代入式(2)可分别得出两侧齿面上的接触压力p(zi),再将p(zi)代入式(1)即可分别得出第i圈螺纹左、右两侧面上的摩擦扭矩Til、Tir,则第i圈螺纹上总的摩擦扭矩为

(4)

因此,接头拧紧(机紧)时所需的上扣扭矩T为密封端面上发生的摩擦扭矩Te与管体和接箍上所有发生接触螺纹的摩擦扭矩之和,其值为

(5)

选取图1中截面H-H左侧的管体与接箍为研究对象,管体和接箍机紧时在台阶密封面上发生接触并相互挤压,简化后的受力情况及各尺寸如图4所示。其中D0～D4分别表示对应直径。管体受拉力W′的作用,接箍受压力W的作用,二者满足关系:

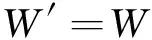
(6)

图4(a)中的管体螺杆(L段)可近似看作等厚度的圆筒,受到拉伸作用时,其产生的变形δP可用式(7)计算:

(7)

式中:EP为管体的弹性模量。

图4(b)中的接箍是一个变截面的圆筒,当受到压紧作用时,其产生的变形δB可采用离散化方法进行计算。

图5所示为管体和接箍机紧时的变形分析。套管接头拧紧到手紧位置后,两密封面之间形成一个初始间隙δ0,如图5(a)所示。从手紧位置起,在上扣扭矩T的作用下,管体密封端面向接箍密封端面逐步靠近。如图5(b)所示,当管体外螺纹轴向旋进量为δ0时,两密封端面发生接触。若继续拧紧,管体外螺纹与接箍内螺纹因径向过盈配合将在密封面上产生压紧力,管体受拉,接箍受压。螺纹接头拧紧N圈后,管体外螺纹尾部螺杆部分(长度为L)因弹性变形产生一个伸长量δP;接箍内螺纹在拧紧过程受到压缩,则必然存在一点,该点(距密封面长度为L-δ0+NP-δB)旋进后与管体外螺纹右端面上的点啮合。

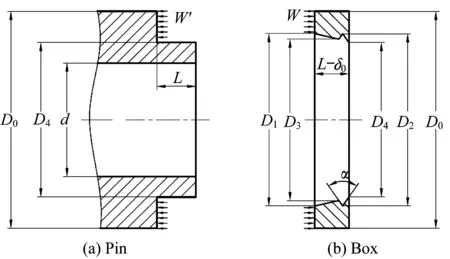
图4 简化后管体与接箍的受力情况Fig.4 Simplified load situations of the pin and box

图5 管体与接箍拧紧变形分析Fig.5 Deformation analysis of the pin and box in power-tight position

由图5可知,在弹性范围内,管体与接箍受力变形后存在关系式:

(8)

式中:L为管体外螺纹尾部螺杆长度;δB为接箍压缩变形量;δP为管体拉伸变形量。整理式(8)得

(9)

图6所示为接箍几何尺寸与变形计算方法,接箍变形δB由AB、BC、CD3段变截面圆筒的变形组成(如图6(a)所示)。油套管接头的螺纹锥度很小,接箍内螺纹相邻两牙对应点的径向厚度可认为近似相等,则δB为

(10)

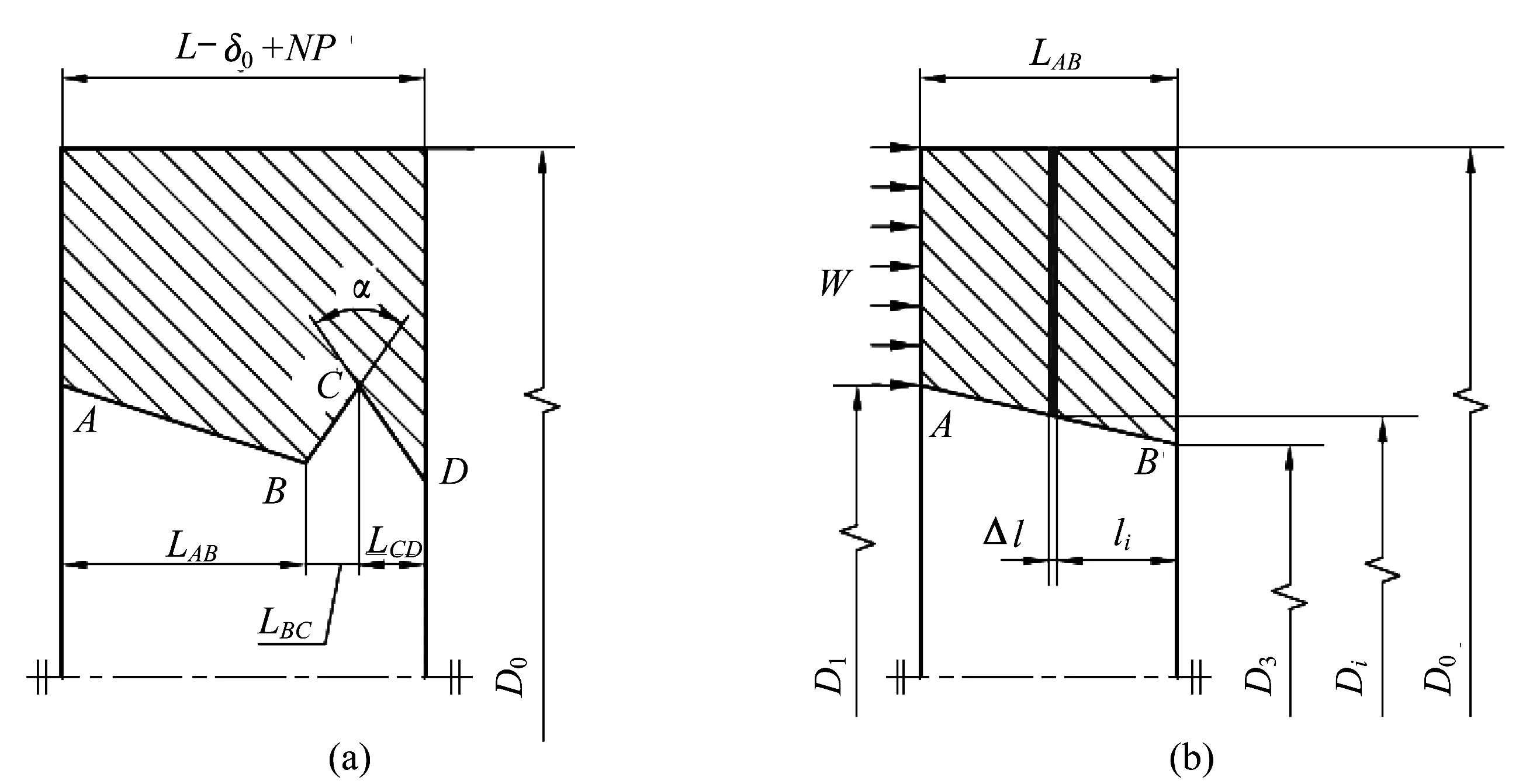
图6 接箍几何尺寸与变形计算Fig.6 Geometry dimension and deformation calculation of the box

式中,K为接箍端面一侧未发生啮合的螺纹牙数。

由图4(b)和图6(a)可知,BC、CD段圆筒的轴向长度LBC、LCD分别为

(11)

(12)

则AB段圆筒的轴向长度LAB为

(13)

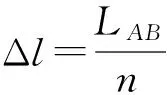
(14)

式中:EB为接箍的弹性模量;Di为AB段接箍第i段圆筒的平均直径,其值为

(15)

AB段接箍的变形为

(16)

同理,可计算出BC、CD段接箍的变形分别为

(17)

(18)

式中,Dj、Dk分别为接箍BC、CD第j、k段圆筒的平均直径,其值分别为

(19)

(20)

若管体与接箍材料相同,将式(6)、(7)、(16)、(17)和(18)代入式(9)整理,即可得到计算密封面压紧力的计算模型:

(21)

2 密封端面微观接触分析方法

在本文的研究中,参考文献[15]给出的方法,研究油套管断面处粗糙表面微观接触性能。以螺纹接头两密封接触面为研究对象,图7所示给出了两粗糙密封表面微观接触过程。密封面的间距S(图7(a))是指两接触面的中性平面之间的距离,两接触面在外载荷W作用下开始相互靠近,当接触面上的第一对微凸体发生接触时,接触面间距为S0(图7(b));若继续增大外载荷,两接触表面间产生相互趋近量ΔS,在局部区域发生微凸体接触(图7(c))。

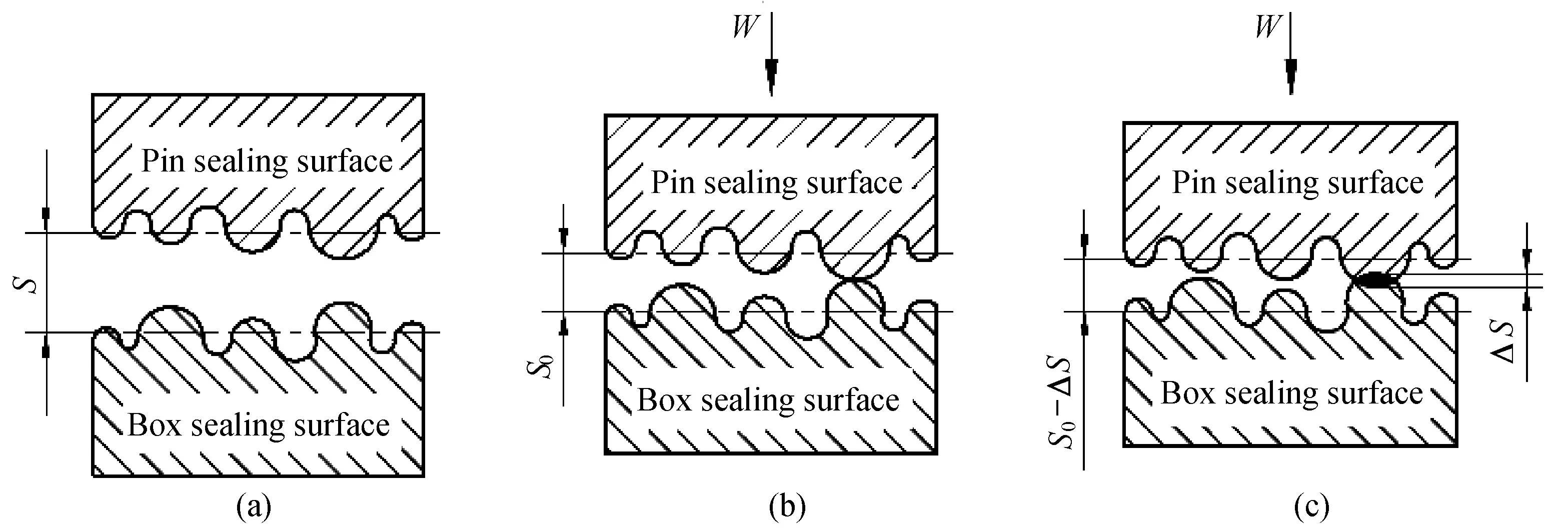
图7 两粗糙密封面微观接触Fig.7 Micro contact procedure between two rough seal surfaces

由文献[15]可知,单个微凸体的接触载荷与施加在接触面上的外载荷W应满足关系:

(22)

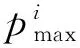
(23)

(24)

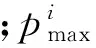
对于整个接触区域,其最大接触应力

(25)

两接触面在外载荷的作用下发生接触,名义接触面积为A0,接触后产生的实际接触面积为A。实际接触面积与名义接触面积比值为

(26)

式中:Ai为第i个接触区域的实际接触面积;m、n为整个接触区域的网格划分数;Ni为第i个接触区域发生接触的网格节点数。

3 模拟计算结果

3.1 计算模型及参数

油套管接头的密封面可采用自相关函数进行计算机数值模拟。本文采用指数自相关函数模拟三维粗糙表面,其形式为

(27)

式中:σ为表面粗糙度均方根;τx、τy分别为x、y方向任意两点之间的距离;βx、βy分别为x、y方向上的相关长度,当βx=βy时表面为各向同性,当βx≠βy时表面为各向异性。

当两密封表面的粗糙度均方根均为σ=1 μm时,模拟出的随机粗糙密封表面如图8所示。

采用上述计算模型与模拟方法,以API套管圆螺纹接头为例进行微观接触性能参数模拟计算。管体与接箍密封面经过机械研磨加工后,σ一般为0.5～2 μm,本算例中σ分别取0.5、1和2 μm。参照API 5B标准,螺纹接头的结构参数与材料物理参数见表1。

3.2 表面粗糙度对微观接触性能参数的影响

模拟计算表面粗糙度对微观接触性能参数的影响时,选择3种不同工况的密封接触面,即一个密封接触面的σ保持不变,另一个发生变化,接触工况与接触参数如表2所示;管体与接箍密封面的初始间隙δ0= 0。

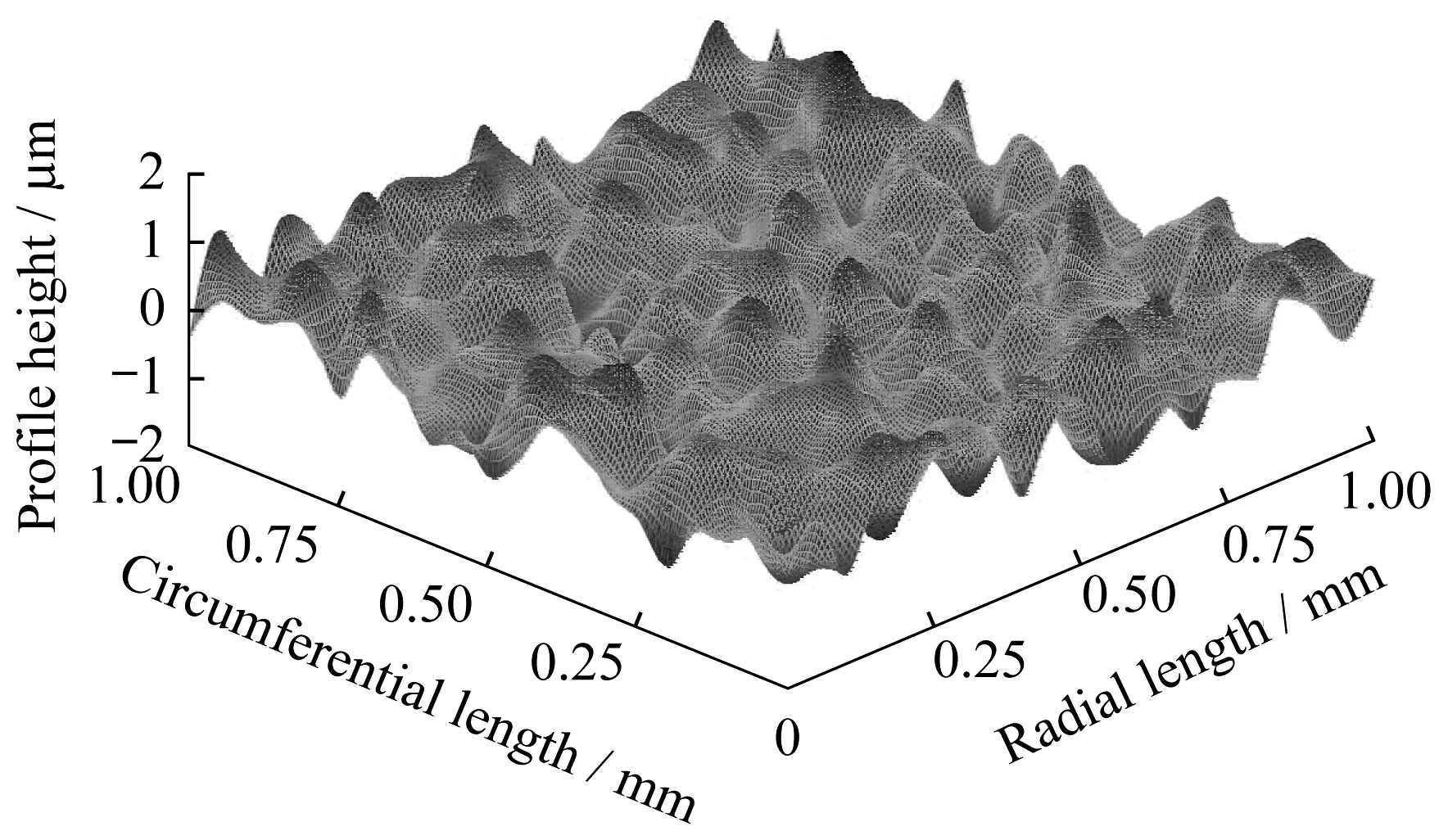
Fig.8 σ=1 μm时的粗糙表面模拟Fig.8 Seal surface modeled with σ=1 μm表1 螺纹接头参数Table 1 Parameters of the threaded connection

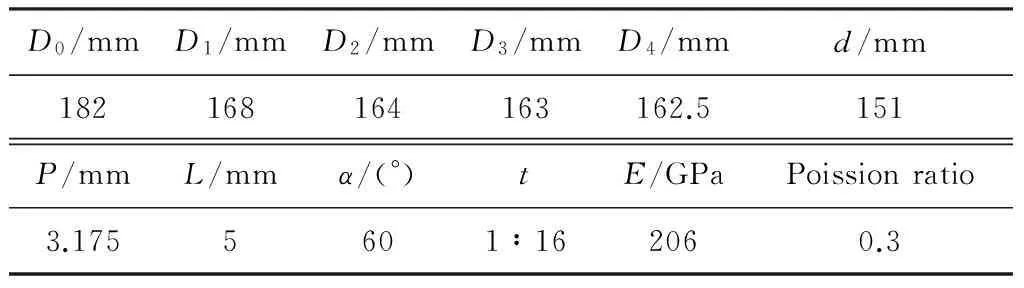
D0/mmD1/mmD2/mmD3/mmD4/mmd/mm182168164163162.5151P/mmL/mmα/(°)tE/GPaPoissionratio3.1755601∶162060.3

表2 接触工况与接触参数Table 2 Contact conditions and parameters

相互趋近量与螺纹拧紧圈数的变化关系见图9。3种工况下相互趋近量与螺纹拧紧圈数的变化规律基本相同:在拧紧起始阶段,随机粗糙表面上发生接触的微凸体的数量极少,微凸体产生弹性变形所需的外载荷相对较小,因此相互趋近量曲线增加速率较快;随着螺纹拧紧圈数稳步增加,越来越多的微凸体发生接触,微凸体产生弹性变形所需的外载荷逐步增大,这时的相互趋近量曲线与拧紧初期相比呈现缓慢上升趋势;当拧紧圈数相同时,密封接触面的粗糙度越大,其相互趋近量就越大。

接触面积与螺纹拧紧圈数的变化关系如图10所示。随着螺纹拧紧圈数的增大,实际接触面积也随之逐渐增大;当螺纹拧紧圈数相同时,密封接触面粗糙度越小,实际接触面积就越大。对锥螺纹接头端面密封来说,密封表面越光滑,其密封性能越好。

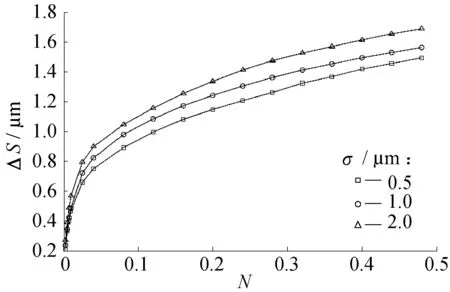
图9 相互趋近量与螺纹拧紧圈数的变化关系Fig.9 Variations of the approaching separation and the tightening cycles for the pin

图10 接触面积与螺纹拧紧圈数的变化关系Fig.10 Variations of contact area and the tightening cycles for the pin

最大接触压力与螺纹拧紧圈数的变化关系如图11所示。随着螺纹拧紧圈数的逐步增大,最大接触压力呈现出先快后慢的增大趋势;当螺纹拧紧圈数大约超过0.1时,最大接触压力开始与外载荷呈近似线性关系;在螺纹拧紧圈数相同的条件下,密封表面越光滑,其最大接触压力越小。

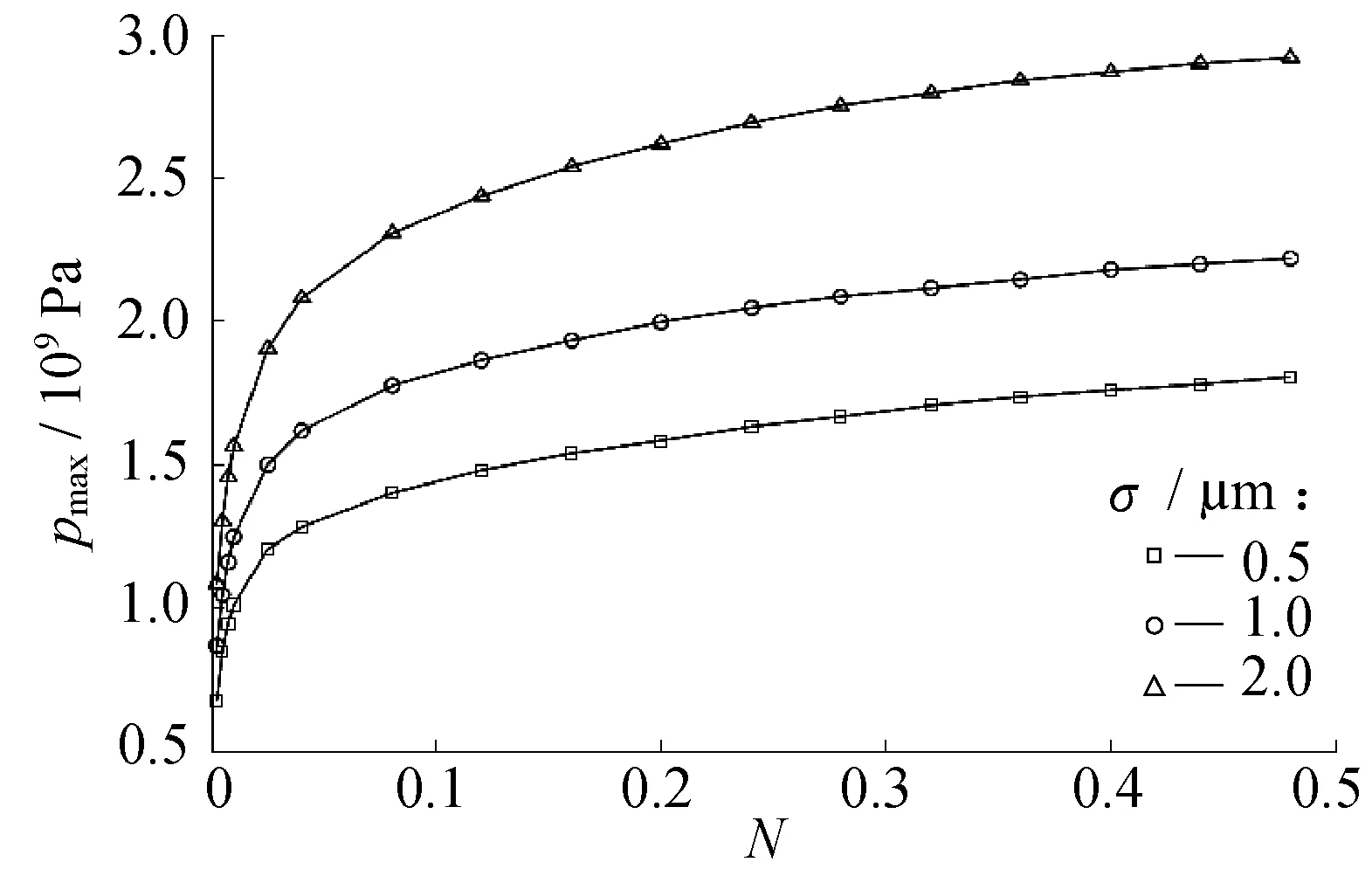
图11 最大接触压力与螺纹拧紧圈数的变化关系Fig.11 Variations of the maximum contact pressure and the tightening cycles for the pin

3.3 初始间隙δ0对微观接触性能参数的影响

模拟计算初始间隙δ0对微观接触性能参数的影响时,两密封面的表面粗糙度均方根相同,均为σ=1 μm,且保持不变,接触面间距S0=2.302 0 μm;管体与接箍密封面的初始间隙δ0选择3种不同工况,分别为0、0.3和0.6 μm。相互趋近量与螺纹拧紧圈数的变化关系如图12所示。

图12 相互趋近量与螺纹拧紧圈数的变化关系Fig.12 Variations of the approaching separation and the tightening cycles for the pin

比较图12与图9可以发现,初始间隙的大小不会改变相互趋近量随螺纹拧紧圈数增大而增大的变化趋势。由图12可知,在拧紧圈数相同的条件下,初始间隙越小,相互趋近量越大;当螺纹拧紧圈数较小时,初始间隙的不同对相互趋近量的影响较为显著。

接触面积与螺纹拧紧圈数的变化关系如图13所示。在3种不同工况下,实际接触面积与螺纹拧紧圈数的变化规律基本相同,即实际接触面积随螺纹拧紧圈数的增大而增大;在拧紧圈数相同的条件下,初始间隙越小,实际接触面积越大。

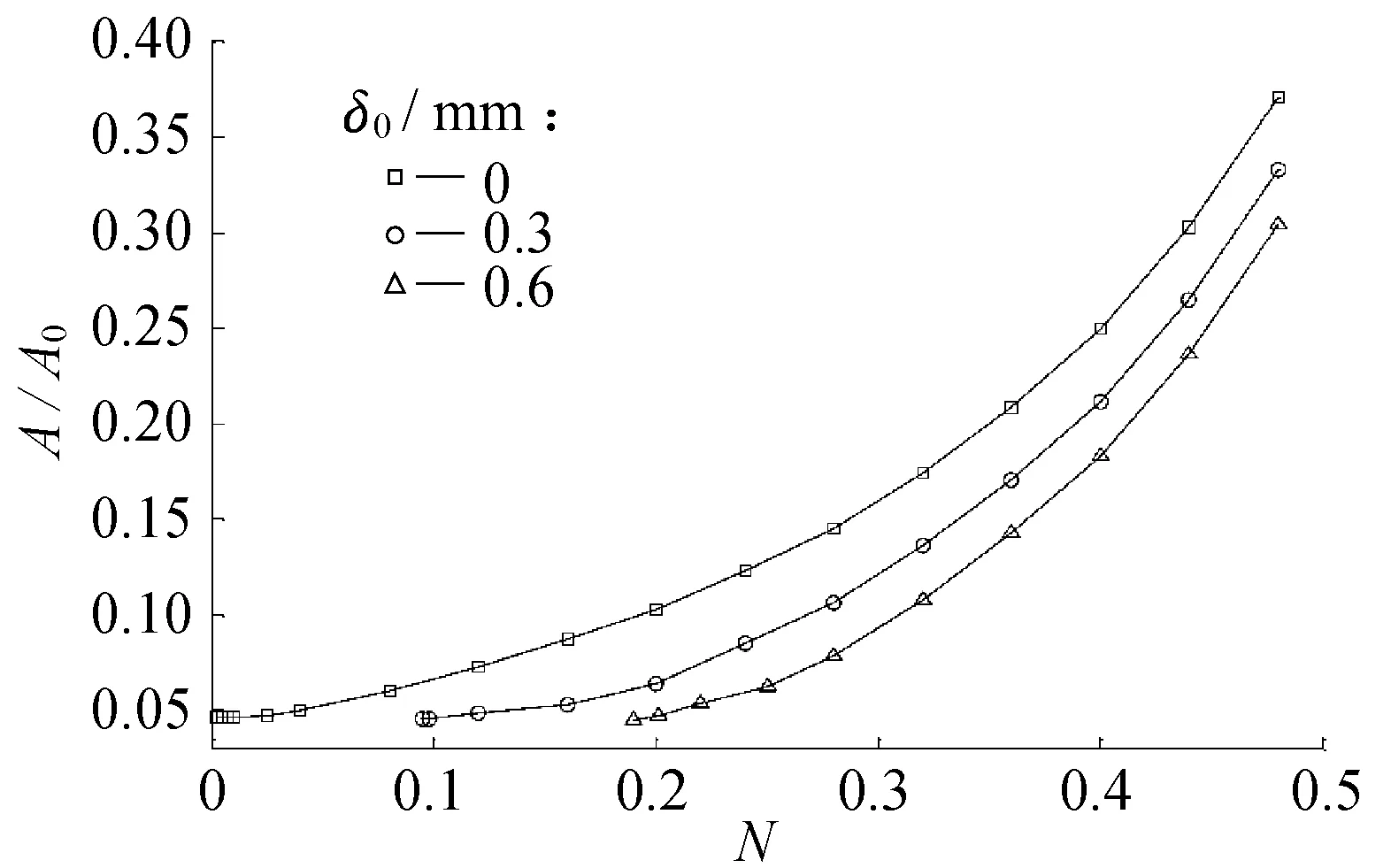
图13 接触面积与螺纹拧紧圈数的变化关系Fig.13 Variations of contact area andthe tightening cycles for the pin

最大接触压力与螺纹拧紧圈数的变化关系如图14所示。比较图14与图11可以发现,初始间隙的大小不会改变最大接触压力随螺纹拧紧圈数增大而增大的变化趋势。由图14可知,在拧紧圈数相同的条件下,初始间隙越小,最大接触压力越大;当螺纹拧紧圈数较小时,初始间隙的不同对最大接触压力的影响较为显著。

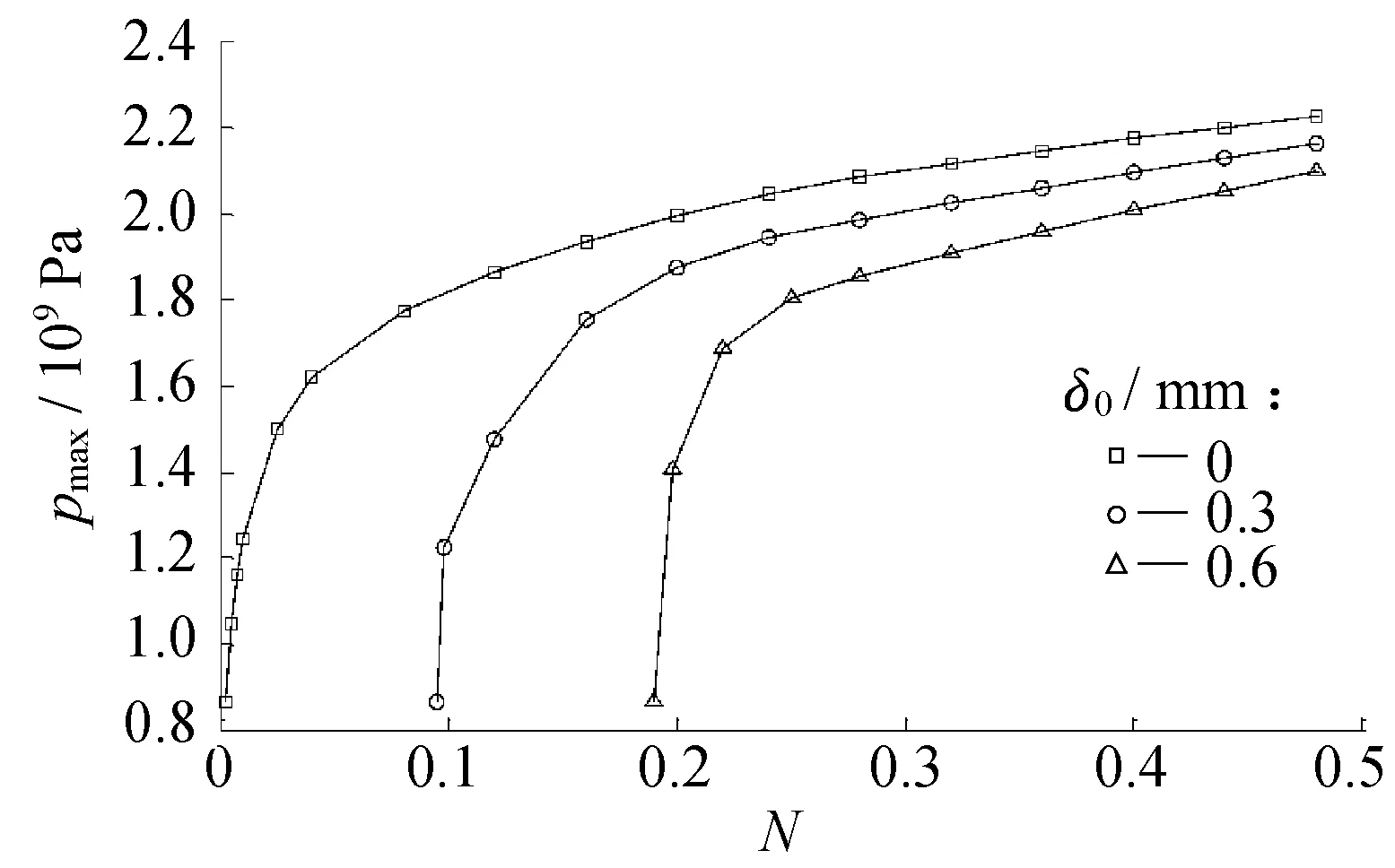
图14 最大接触压力与螺纹拧紧圈数的变化关系Fig.14 Variations of the maximum contact pressure and the tightening cycles for the pin

4 结 论

(1) 在弹性范围内,建立了油套管接头上扣拧紧时能够计算端部密封面上挤压力的力学模型;在此基础上,通过粗糙密封表面微观接触分析,建立了油套管锥螺纹拧紧过程密封接触面上的相互趋近量、接触面积和最大接触应力的计算方法;

(2) 以API圆螺纹套管接头为例进行了分析计算,研究了密封接触端面上的接触面间距、接触面积和最大接触应力与拧紧力矩(圈数)、表面粗糙度和初始间隙的变化关系,得到了具体的变化曲线。结果表明:在弹性范围内,在密封面初始间隙一定的条件下,螺纹拧紧力矩(圈数)增大使相互趋近量增大,接触表面粗糙度越大,其相互趋近量就越大;螺纹拧紧力矩(圈数)增大使实际接触面积增大,粗糙度越小,其实际接触面积就越大;螺纹拧紧力矩(圈数)增大使最大接触应力增大,接触表面粗糙度越小,其最大接触压力就越小。同时,在密封副表面粗糙度一定的条件下,当拧紧力矩(圈数)相同时,初始间隙越小,接触面间距、接触面积和最大接触应力则越大。

[1] MADUSCHKA L.Beansprukung von schraubenverbindungen und zweckmabige gestaltung der gewindeträger[J].Forsch,1936,7:299-305.

[2] SOPWITH D G.The distribution of load in screw threads[J].Proceedings of the Institution of Mechanical Engineers,1948,159:373-383.

[3] BRUSCHELLI L,LATORRATA V.The influence of “Shell Behavior” on load distribution for thin-walled conical joints[J].Journal of Applied Mechanics,2000，67(2)：298-306.

[4] WANG W,MARSHEK K M.Determination of the load distribution in a threaded connector having dissimilar materials and varying thread stiffness[J]．Journal of Manufacturing Science and Engineering,1995,117(1):1-8．

[5] 高连新,金烨.套管连接螺纹的受力分析与改善措施[J].上海交通大学学报,2004,38(10):1729-1732.

[6] CHEN Shoujun,AN Qi,ZHANG Yi,etal.Research on the calculation method of tightening torque on p-110s threaded connections[J].Journal of Pressure Vessel Technology,2011,133(10):051207.

[7] CHEN Shoujun,LI Qiang,AN Qi.Calculation method of radial stress and deformation on conic threaded connections with interference Fit[J].Frontiers of Mechanical Engineering in China,2010,5(3):302-307.

[8] 申昭熙,王鹏,李磊,等.特殊螺纹接头密封可靠性数值分析[J].石油矿场机械,2012,41(1):10-13.

[9] 申昭熙,李磊,王鹏,等.特殊螺纹接头主要参数对密封性能的影响分析[J].石油矿场机械,2011,40(1):38-41.

[10] 周鑫,庞贺伟,刘宏阳,等.球面密封结构密封状态的力学分析及验证[J].中国空间科学技术,2007,27(2):42-46.

[11] MURTAGIAN G R,FANELLI V,VILLASANTE J A,etal.Sealability of stationary metal-to-metal seals[J].Journal of Tribology,2004,126:591-596.

[12] JUN Takano,MASAO Yamag uchi,HIDENO ri Kunishige.Development of premium connection ‘ KSBEAR’ for withstanding high compression,high external pressure,and severe bending[J].Kawasake Steel Technical Report,2002(47):14-22.

[13] MARIE C,LASSEUX D.An integrated approach to characterize liquid leakage through metal contact seal[J].European Journal of Mechanical and Environmental Engineering,2003,48:81-86.

[14] 蔄靖宇,李正美,安琦.油套管接头台阶密封面的接触压力及密封性能[J].华东理工大学学报(自然科学版),2015,41(3):417-423.

[15] MAN Jingyu,ZHOU Qiong,TAO Zongjie,etal.Micro-scale numerical simulation on metal contact seal[J].Journal of Mechanical Engineering Science,2014,228(12):2168-2177.

Micro-Scale Contacting Numerical Simulation on Shouldered Face Seal of Tubing and Casing Threaded Connection

MAN Jing-yu1,2, HUANG Long-wen1, AN Qi1

(1.School of Mechanical and Power Engineering, East China University of Science and Technology, Shanghai 200237, China; 2.School of Mathematics and Physics,Shanghai University of Electric Power, Shanghai 200090, China)

Tubing and casing connections are widely used in oil and natural gas industry.Their seal performance is very important for circumstance and production safety in oil and gas well.In this paper,the threaded connections in the tightening condition are taken as research objects and a calculation approach to the squeezing force on the shouldered seal face of a conical threaded connection is established in the elastic range.By the method of micro contact analysis on sealing rough surface,API round threaded casing connection is taken as the calculating sample,and the influences of tightening torque (tightening cycles),roughness and initial seal clearance on the seal performance of the shouldered face are numerically simulated.And the concrete variation curves are obtained and analyzed in detail.

tubing and casing threaded connection; shouldered face seal; contact pressure; rough surface; numerical simulation

1006-3080(2016)05-0722-08

10.14135/j.cnki.1006-3080.2016.05.021

2016-04-13

蔄靖宇(1972-)，男，博士生，讲师，研究方向为机械设计及理论。

安 琦，E-mail:anqi@ecust.edu.cn

TH131.3;TH123.4;TE256.9

A