基于三维有限元法的球面-锥面特殊扣密封性分析

于 洋，张佳浩，韩鑫

（西安石油大学机械工程学院，陕西 西安 710065）

随着石油天然气开采开发中高温高压井、深井超深井以及腐蚀环境井等复杂环境井的开发不断深入，以及井下开采环境的不断恶化，复杂油气田的开采开发对油气井管柱完整性和安全可靠性提出了更高要求。经统计，高温高压气井中套压升高多是由特殊扣密封失效引起的[1]。特殊扣的密封能力与产品的设计、加工、材料性能、表面处理工艺以及现场施工质量、使用工况密切相关。由于材料非线性、载荷非线性和边界条件非线性的多重非线性效应，难以用解析方法描述接头密封完整性问题[2-3]，而全尺寸试验法周期长，费用昂贵，且对试验设备性能要求较高。为此本文采用有限元法建立某球面-锥面的特殊扣三维有限元模型，分析在拉伸载荷和内压载荷作用下，特殊扣主密封面及扭矩台肩处的等效应力和接触压力分布，以了解特殊螺纹接头在外载作用下的密封性能。

1 球面-锥面特殊扣有限元模型

不同于API油管扣以螺纹脂填充螺纹间隙实现密封，特殊扣在螺纹端面设计了独立的密封结构，扭矩台肩起过扭保护与辅助密封的作用，螺纹部分只起连接作用[4]，API油管扣与特殊扣结构对比如图1所示。目前常用的特殊扣密封面结构有锥面-锥面、球面-锥面、球面-柱面，按照密封形式可分为面密封和线密封。本文以Φ88.9mm×6.45mm P110某球面-锥面特殊扣为研究对象，特殊扣的主要参数如下：密封面锥度1∶2；螺纹锥角1∶16，螺纹牙承载面角度-3°，螺纹牙导向面角度10°。考虑特殊扣关于中心径向截面对称，仅选取一侧的特殊扣进行三维建模，在中心径向对称截面上施加轴向全约束，在油管端中心点上施加轴向力载荷，内部施加压力载荷。事件对称材料屈服极限为758MPa。使用HyperMesh软件对特殊扣进行前处理，细化密封面及台肩处的网格，经统计，接箍网格数量为34593，接头网格数量为32291，密封面处网格数量为8640。特殊扣整体采用C3D8R单元类型，网格划分情况如图2。

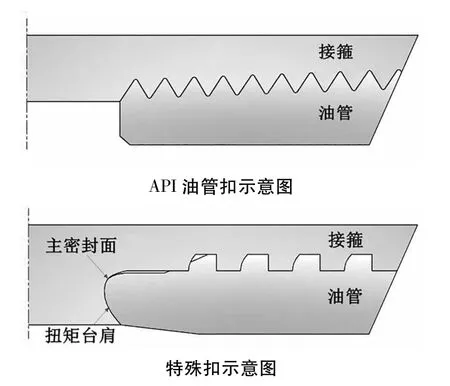
图1 API油管扣与特殊扣结构对比图

图2 球面-锥面特殊扣网格划分与约束

2 上扣扭矩作用下球面-锥面特殊扣密封面接触压力分析

保证特殊扣密封性能的前提是控制合理的上扣扭矩，生产厂家会推荐最小、最佳、最大的上扣扭矩值。根据现有文献研究[5-7]，在特殊扣受拉力作用下，密封台肩处的接触压力会减小。因此，本文选取厂家推荐的最大上矩进行上扣，研究球面-锥面特殊扣密封面上接触压力分布规律。特殊扣在最大扭矩上扣后，整体等效Mises应力分布云图如图3所示，最大等效Mises应力出现在扭矩台肩上，其值为749.3MPa，小于材料屈服强度，并未发生塑性变形。等效应力从扭矩台肩、密封面、螺纹处依次减小。说明扭矩台肩承担了较大的扭矩，这与扭矩台肩防过扭的设计理念一致。

图3 特殊螺纹扣Mises等效应力云图（最大上扣扭矩）

3 拉力作用下锥面-球面特殊扣密封面接触压力分析

对于球面-锥面特殊扣，按照最大上扣扭矩上扣之后，对特殊扣施加800kN拉伸载荷，特殊扣整体Mises等效应力分布如图4。由图4可知，最大等效应力出现在密封面及扭矩台肩上，为765.3MPa，由于最大等效应力超出了材料的屈服极限，特殊扣密封部分将发生塑性变形，将不利于特殊扣的再次使用。

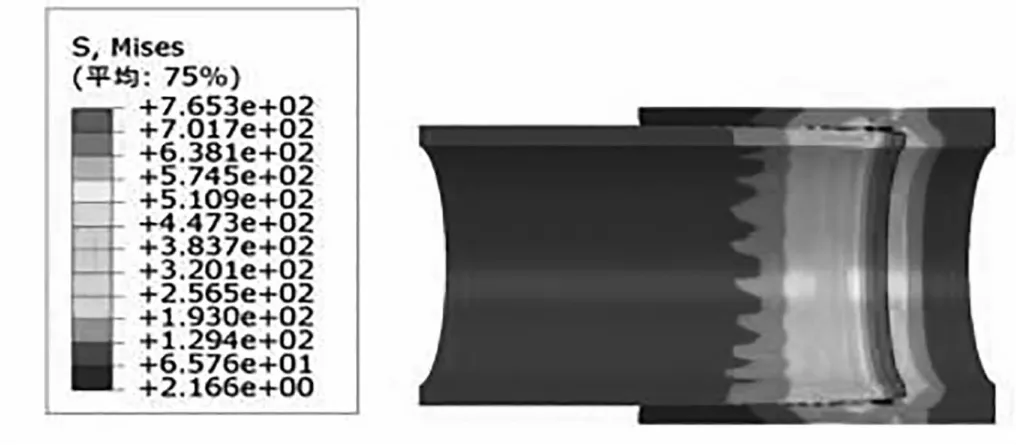
图4 特殊扣Mises等效应力分布（最大上扣扭矩+轴向拉力）

从主密封面到台肩面，沿锥度方向等间距选取12个节点，编号为1～12，密封面上节点记为1～6，台肩面节点记为7～12，提取各节点上的接触压力值，绘制密封面-台肩面接触压力变化曲线如图5。由图5可知，最大接触压力出现在球面-锥面密封的起始位置，接触压力整体呈减小趋势。计算密封面上平均接触压力值为360.5MPa，密封面接触长度为0.8mm，与仅受上扣扭矩时相比较，平接触压力减小了0.5%。台肩处的接触压力小于主密封面的接触压力，此结果与扭矩台肩的辅助密封作用相契合。台肩面上接触压力呈现递减趋势，最大接触压力在节点7处，为327.6MPa，在台肩面末端，接触压力降低至0。进一步研究密封面接触压力变化规律，在密封面上选取节点2和节点6，绘制沿密封面环向路径密封面接触压力变化曲线如图6。由图6可知，环向路径上的接触压力分布均匀，节点6为密封面前段接触压力较大，节点6为密封面后段接触压力较小。因此，锥面-球面特殊扣主要靠密封面的前段实现密封。

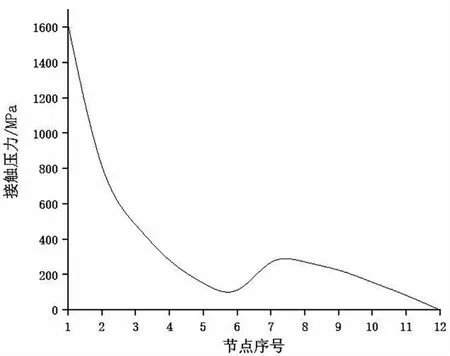
图5 密封面-台肩面接触压力分布规律

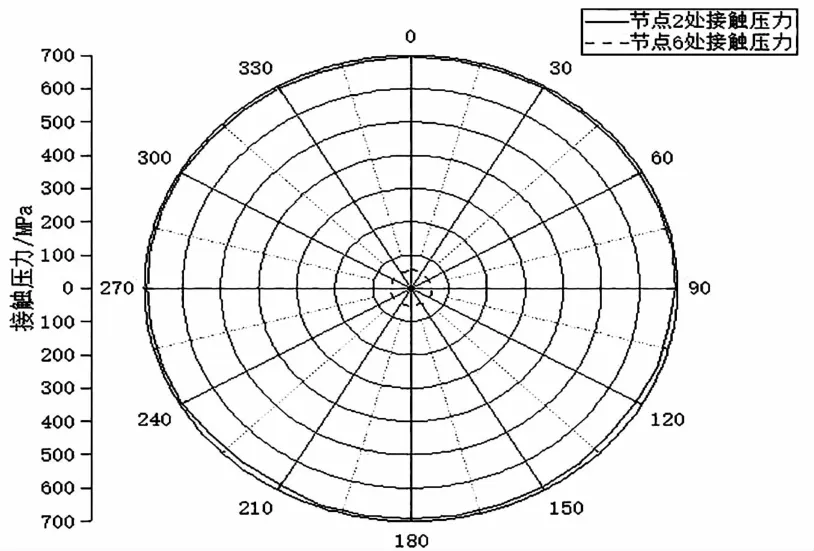
图6 沿环向路径密封面节点2和节点6处接触压力

4 内压作用下球面-锥面特殊扣密封面接触压力分析

按最大上扣扭矩上扣之后，再在管体内部施加80MPa内压，特殊扣Mises等效应力分布如图7。

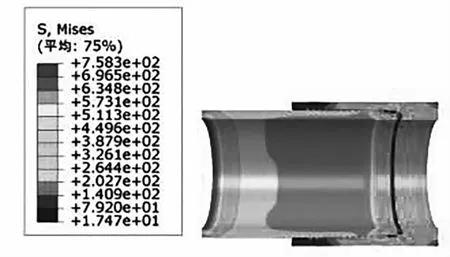
图7 特殊扣Mises等效应力分布（最大上扣扭矩+内压）

由图7可知，在内压作用下，最大Mises应力为758.3MPa，趋近于材料屈服极限，未发生塑性变形，可以保证密封强度。

沿密封面-台肩面等间距取12个节点，其中1-6节点在密封面上，7-12为台肩面上的节点，绘制密封面-台肩面接触压力分布规律曲线如图8。

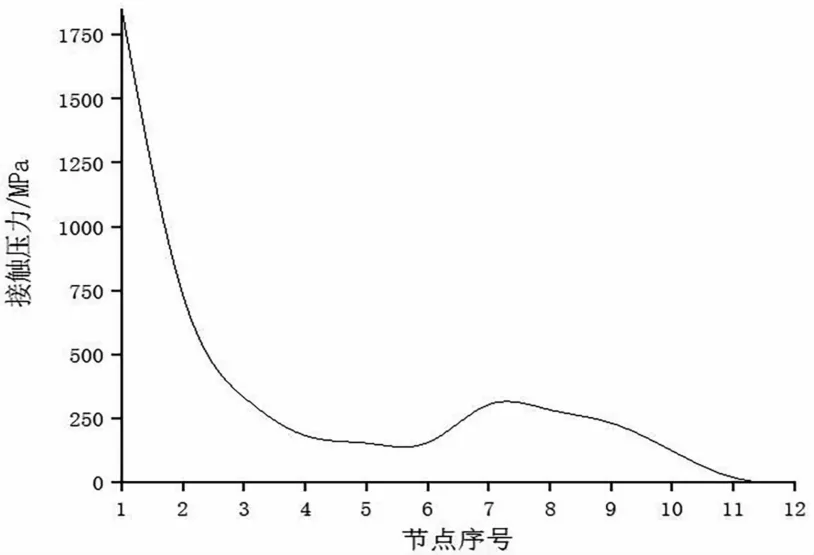
图8 密封面-台肩面接触压力分布规律

由图8可知，密封面上接触压力呈减小趋势，计算密封面上平均接触压力值为365.8MPa，密封接触长度为1.15mm。台肩面上接触压力也呈现递减趋势，最大接触压力出现在节点7处，为334.7MPa。

在密封面上选取节点2和节点6，绘制沿密封面环向路径密封面接触压力变化曲线如图9所示。由图9可知，环向路径上节点2的接触压力分布均匀，节点6处接触压力有突变，这是因为80MPa的内压改变了密封面的接触形状。

图9 环向路径密封面节点2和节点6处接触压力

5 结论

通过研究球面-锥面特殊扣在不同载荷下密封面接触压力和等效应力的分布规律，得到以下结论：

1）以最大扭矩上扣时，特殊扣Mises等效应力从扭矩台肩、密封面、螺纹处依次减小。说明扭矩台肩承担了较大的扭矩，这与扭矩台肩防过扭的设计理念一致。2）最大上扣扭矩和800kN拉伸载荷作用时，特殊扣的最大Mises等效应力出现在密封面起始处，部分位置的Mises等效应力大于材料屈服强度，在台肩面上出现应力集中；接触压力沿锥度方向整体呈现减小趋势，环向路径接触压力分布较为均匀。因此，800kN拉伸载荷会降低特殊扣的密封效果，但并未发生泄漏。3）最大上扣扭矩和80MPa内压作用时，特殊扣上的最大Mises等效应力趋近于材料屈服极限，在密封面上有足够大的接触压力；密封面环向路径上平均接触压力值较大，密封面接触长度为较大，但在密封面后段接触压力分布不均匀，因此，80MPa的内压改变了密封面的接触形状，会影响特殊扣的密封效果。