方形高强钢管混凝土叠合柱轴压极限承载力分析
2016-11-21赵均海侯玉林张常光
赵均海,侯玉林,张常光
(长安大学 建筑工程学院, 西安 710061)

方形高强钢管混凝土叠合柱轴压极限承载力分析
赵均海,侯玉林,张常光
(长安大学 建筑工程学院, 西安 710061)
对于新提出的方形高强钢管混凝土叠合柱的极限承载力,基于统一强度理论,考虑中间主应力和材料拉压比的影响,引入有效约束系数和非有效约束系数并考虑箍筋对钢管外混凝土约束作用的不同,把钢管外箍筋约束混凝土划分为有效约束区和非有效约束区,将方形截面等效为圆形截面以考虑钢管核心混凝土受到的钢管和外围钢筋混凝土的双重约束效应,提出了方形高强钢管混凝土叠合柱的一种新的轴压极限承载力计算方法。将所得理论计算结果与文献试验结果进行对比,吻合良好,证明了公式的正确性。对各参数的影响规律分析表明,方形高强钢管混凝土叠合柱的承载力随着侧压系数、中间主应力影响系数、材料拉压比和纵向配筋率的增大而增大,随着钢管径厚比的增大而减小。
钢管混凝土叠合柱;箍筋约束;强度理论;极限承载力
高强钢管混凝土叠合柱是由截面中部的高强钢管混凝土柱和钢管外的钢筋混凝土叠合而成的柱,也可以看成是在钢筋混凝土内置钢管混凝土而成的柱,内截面钢管形式有圆钢管、方钢管和矩形钢管,又可称为核心高强钢骨混凝土组合柱。高强混凝土有强度高、变形小的优点,但其延性差、脆性大,不利于抗震;将其与钢管结合,可以充分发挥二者的性能,同时也具有较好的变形能力、较大的刚度和良好的抗火性能等优点,经济效益良好[1-2]。

目前,对于高强钢管混凝土叠合柱轴压承载力的计算,部分研究只考虑钢管对混凝土的约束作用而未考虑箍筋的约束作用;部分考虑钢管对混凝土的约束作用和箍筋对混凝土的约束作用,但均未考虑外围混凝土对钢管内混凝土的约束,即未考虑钢管内混凝土受到的双重约束。在实际工程中,叠合柱配箍量较多,在达到极限状态时,外围箍筋约束混凝土不会过分剥离,能和钢管内混凝土共同承担荷载。而尧国皇[11]的有限元结果也表明钢管核心混凝土受到钢管和外围钢筋混凝土的双重约束,其承载力比同样条件下普通钢管混凝土中混凝土要大。因此,考虑内部混凝土受到的双重约束作用是有必要的。本文以内配圆钢管的方形截面高强钢管混凝土柱为研究对象。构件处于较高应力状态时,箍筋约束混凝土角部受到约束强,边缘中部受到的约束弱,对箍筋约束混凝土利用Mander模型[12]进行有效约束区和非有效约束区的划分,推导出有效约束区系数和非有效约束区系数,同时,本文考虑钢管核心混凝土受到钢管和外围钢筋混凝土的双重约束效应,基于统一强度理论对钢管和钢管约束混凝土承载力分析,推导出方形截面高强钢管混凝土叠合柱的轴压极限承载力,与文献试验值对比验证,并分析了径厚比、中间主应力影响系数、材料拉压比、纵筋配筋率、侧压系数的影响特性。
1 双剪统一强度理论
俞茂宏以双剪单元体和双剪屈服准则为基础,考虑应力状态的所有应力分量以及它们对材料屈服和破坏的不同影响,建立了一个全新的强度理论和一系列新的典型计算准则。统一强度理论包含了无限多个计算准则,几乎可以适用于各种材料,应用十分方便。其表达式为[13]
(1)
(2)
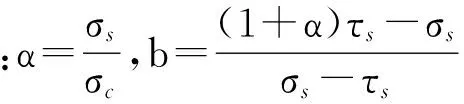
式中:σ1、σ2、σ3为材料第1、第2、第3主应力;σs为材料的拉伸屈服极限;σc为材料的压缩屈服极限;τsv为剪切屈服极限;α为材料的拉压比;b是反应中间主应力以及相应面上的正应力对材料破坏影响程度的参数,0≤b≤1。
2 极限承载力的计算
2.1 箍筋约束钢管外混凝土承载力
实际工程中,构件达到极限状态时,内部钢管的横向变形较小,故不再考虑钢管变形对箍筋约束混凝土的影响[1]。研究表明,方形截面的箍筋对混凝土约束较弱,且对混凝土的约束不均匀,仅在箍筋转角处对混凝土有较大的约束[8]。箍筋约束混凝土有效约束区和非有效约束区划分如图1所示。
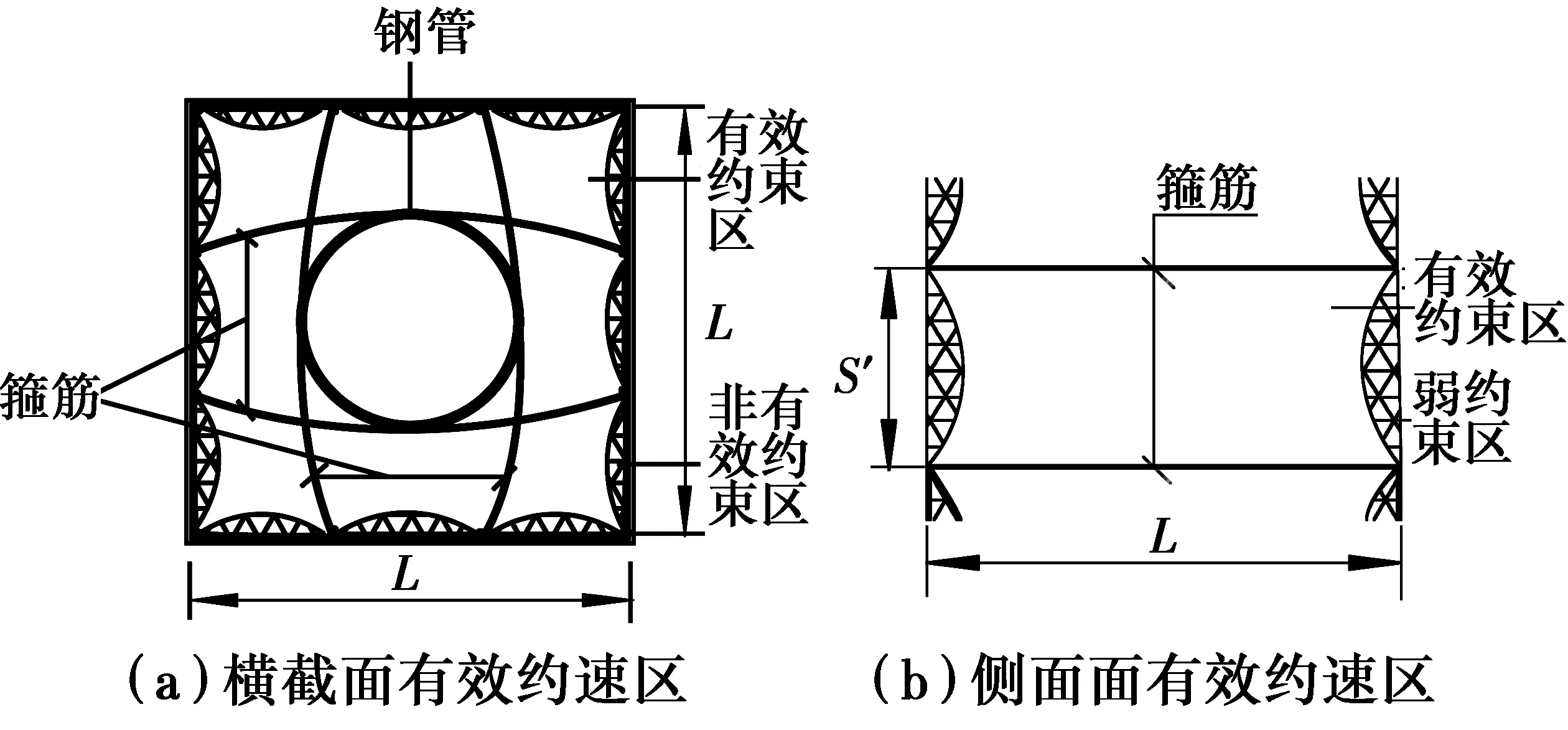
图1 箍筋约束混凝土的有效约束区Fig.1 Effectively confined core for hoop
根据Mander[12]有效约束力概念,定义有效约束面积系数ke。
(3)
式中:ke1为横截面有效约束系数;ke2为侧面有效约束系数。
约束面的边界线为二次抛物线[14],Mander等建议边界线切角θ为45°。且距离角部0.05(L/n1)范围内为有效约束区[15],则单个非有效约束区面积A1为
(4)
式中:n1为横截面每边被箍筋分开的段数;L为除去保护层厚度的构件截面宽度。
非有效约束区总个数为m=4n1个,非有效约束区的总面积为
(5)
则有效约束区面积Ac2为
(6)
式中:D为钢管混凝土的外径。
ke1为横截面有效约束区面积与横截面总面积的比值。由式(5)、(6)可得
(7)
ke2为侧面有效约束区面积与侧面总面积的比值。
(8)
式中:s′为箍筋净距。
故可得
(9)
同理,定义非有效约束区系数ke′。
(10)
式中:ke1′为横截面非有效约束区系数;ke2′为侧面非有效约束区系数。
类似上述推理可得
(11)
基于文献[8]的假设:箍筋对其约束混凝土的约束应力均匀分布,则箍筋受力如图2所示。
由力平衡得
(12)
式中:fr为箍筋对混凝土的均匀约束应力;s为箍筋间距。

图2 箍筋受力分析Fig.2 Stress analysis of
假定应力状态0>σ1=σ2>σ3,满足式(2)条件,且取混凝土受压为正,可得混凝土三向受力状态下轴压强度[16]为
(13)
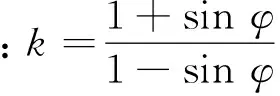
对于有效约束区混凝土,处于三向受力状态。受到箍筋的有效侧压力为kefr[18],代入式(13)可得其轴压强度为
(14)
对于非有效约束区混凝土,侧压力保守的取为ke′fr,同理得其轴压强度为
(15)
2.2 钢管承载力
本文采用双剪统一强度理论计算内置的圆钢管受环向压力时的塑性极限荷载。试件达到极限承载力时,钢管已经屈服[8]。设内钢管径向压力为ps1,钢管的塑性极限荷载[16]为
(16)
式中:σs为钢管的屈服强度;ri为钢管内半径;ti为钢管壁厚。
由塑性力学厚壁圆筒理论[19]得
(17)
式中:fa为钢管的轴向应力;αn为内置钢管混凝土的名义含钢率,定义为钢管和其内包混凝土的面积比。
2.3 钢管约束混凝土的承载力
基于文献[8]的结论,本文考虑钢管外围混凝土对钢管混凝土的约束作用。且箍筋对混凝土的约束作用均匀分布。而方钢管对于混凝土的约束效应,等同于间距为零的箍筋对混凝土的约束承载力的效应。方钢管轴压承载力的计算过程中,认为钢管对混凝土的约束也均匀分布[18]。箍筋约束混凝土和厚度与箍筋直径相同的钢管约束混凝土,二者不同的是侧面对于混凝土的约束:钢管是连续的,箍筋是间断的。本文在方钢管的基础上引入侧向约束系数ke2来考虑箍筋对混凝土约束的不均匀性,从而将箍筋约束混凝土转化为方形钢管约束混凝土。
按照截面面积和含钢率相等将方钢管的有效约束应力等效为圆形钢管混凝土的侧压力p,则外围混凝土和钢管受力如图3所示。
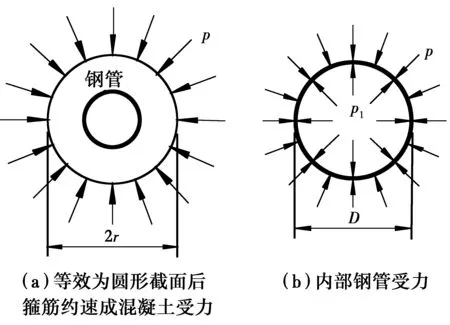
图3 外围混凝土和钢管受力Fig.3 Stress analysis of outside concrete and steel
由材料力学可知
(18)
式中:R和r分别为等效圆钢管的外径和内径;t为箍筋直径。
钢管受到的径向净内压力为
(19)
所以钢管约束混凝土受到的约束力为(p+ps1),由统一强度理论得其轴向强度为
(20)
式中:fci为钢管约束混凝土圆柱体的轴心抗压强度,fci=mfc;m按文献[20]取值。
2.4 钢管混凝土叠合柱轴压承载力
在构件达到极限承载力之前,外侧的保护层混凝土早已被压碎[21],因此,在本文计算承载力时不再考虑混凝土保护层对极限承载力的贡献。并且在构件达到极限承载力时钢管和纵向钢筋已经屈服。方形高强钢管混凝土叠合柱的承载力由箍筋约束钢管外混凝土、纵筋、钢管、钢管约束混凝土构成。计算公式为
(21)
式中:fc1为箍筋非有效约束混凝土轴心抗压强度,由式(15)可得;fc2为箍筋有效约束混凝土轴心抗压强度,由式(14)可得;fc3为钢管约束混凝土轴心抗压强度,由式(20)可得;fa为钢管纵向强度,由式(17)得到;fy为纵向钢筋屈服强度;Ac1为箍筋非有效约束混凝土的横截面积,由式(5)得到;Ac2为箍筋有效约束混凝土的横截面积,由式(6)得到;Ac3为钢管约束混凝土的横截面积;As1为钢管的横截面积;As2为纵向钢筋的总横截面积。
3 算例验证与分析
3.1 计算结果对比
由于钢材的拉压强度相近,取拉压比为α=1,取k=2.1,b=1时[16],将文献[22]和文献[23]中的部分试验数据代入式(21)中进行计算并与试验值对比,结果见表1。
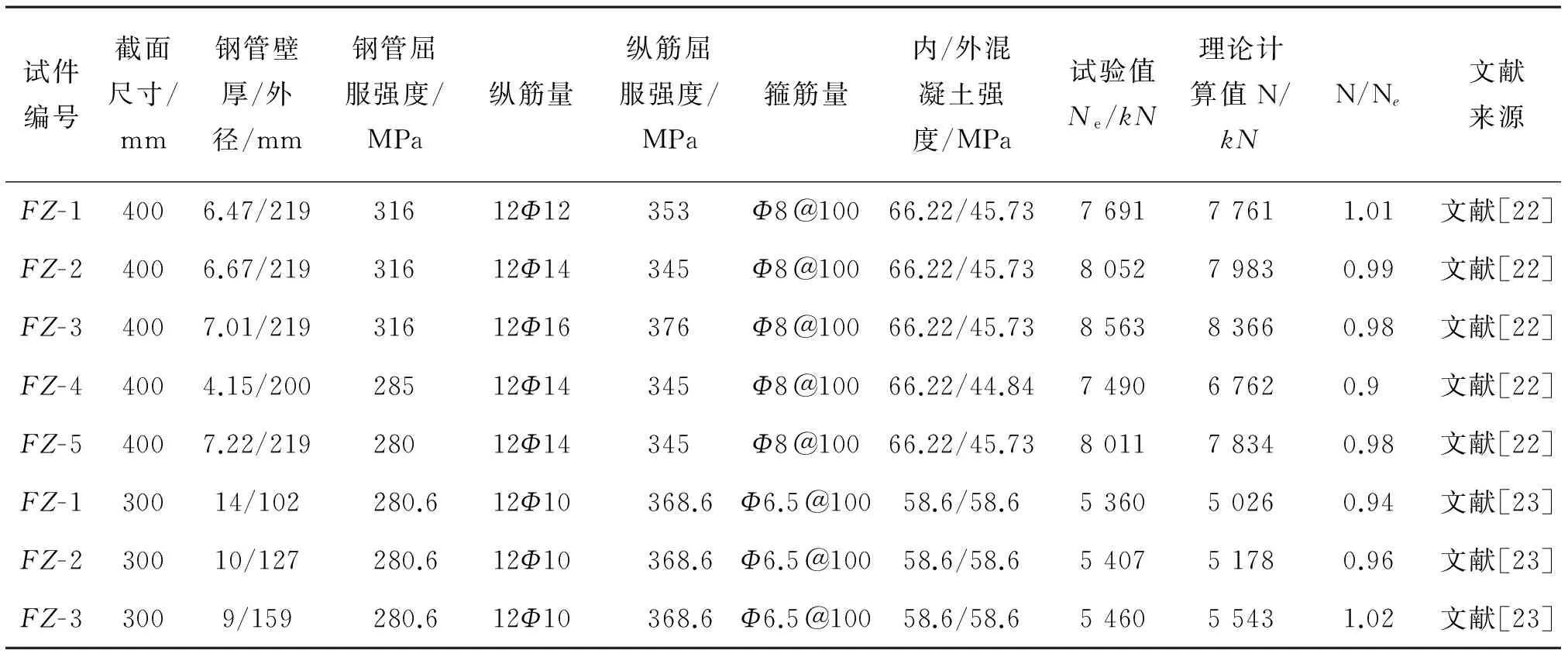
表1 承载力计算值与试验值对比Table 1 Comparison between calculated values and test results
注:Ne试验结果或数值模拟结果,N为本文计算结果;文献[22]中箍筋屈服强度330 N/mm2;混凝土强度为立方体抗压强度。文献[23]中箍筋屈服强度300.2 N/mm2;混凝土强度为轴心抗压强度。
3.2 影响因素分析
3.2.1 侧压系数和纵向配筋率的影响 取文献[22]中试件FZ-2和FZ-3柱为对象,取不同的侧压系数k值(1.5、2.0、2.5、3.0)以及不同的纵向钢筋配筋率(0.85%、1.15%、1.51%),得到的极限承载力的变化情况如图4、图5所示。
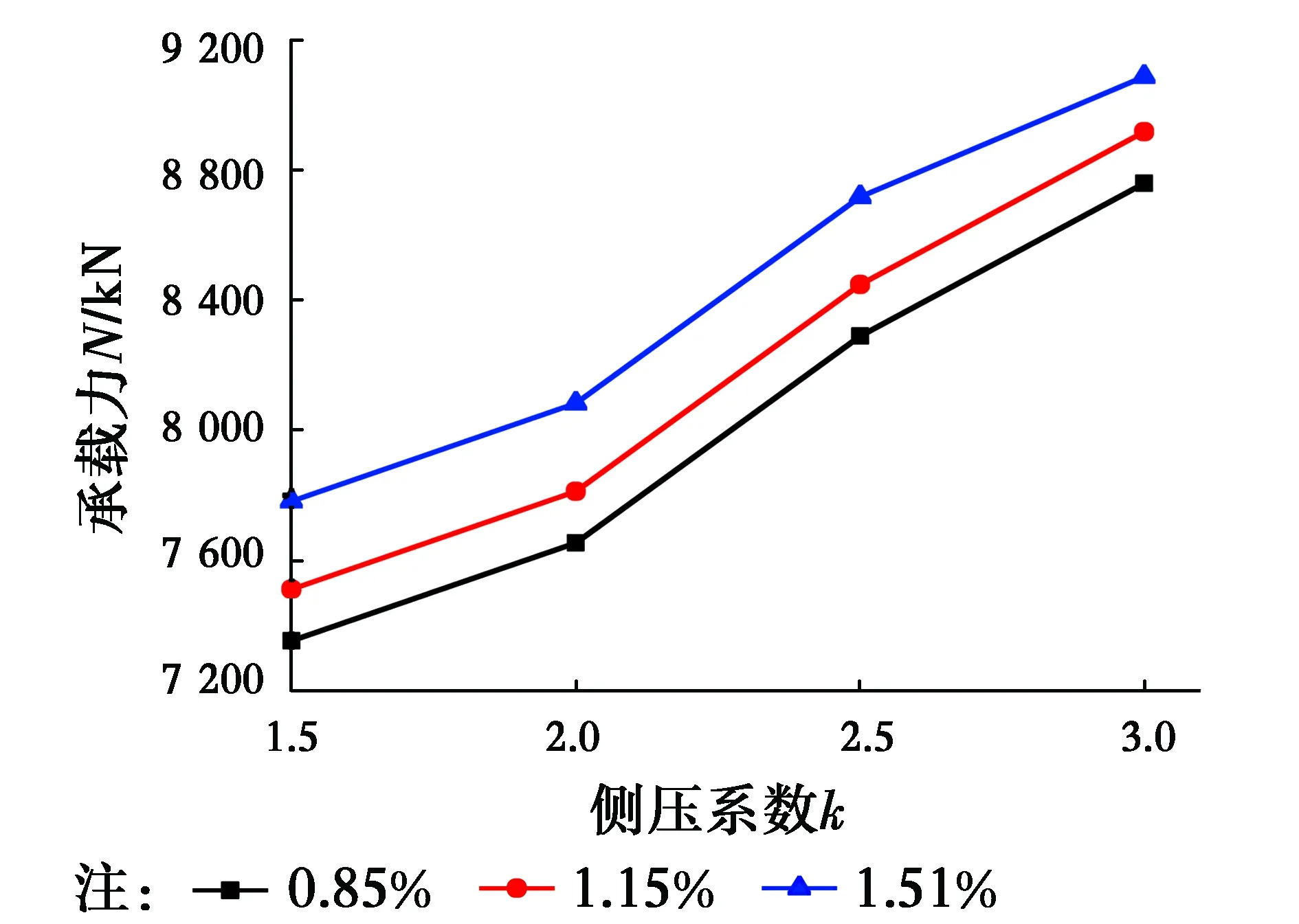
图4 FZ-2柱侧压系数和纵向配筋率对Nu的影响Fig.4 The influence of k and the longitudinal reinforcement ratio on Nu of FZ-2
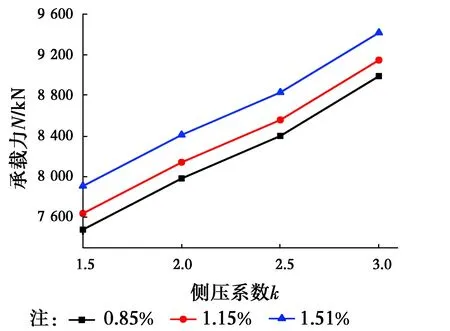
图5 FZ-3柱侧压系数和纵向配筋率对Nu的影响Fig.5 The influence of k and the longitudinal reinforcement ratio onNu of
试件破坏时,纵筋已经屈服[8],在一定范围内,纵向配筋率的增加会贡献更多的承载力。图中也可以看出:承载力随着纵向配筋率的增大而增大;侧压系数越大,对混凝土的约束越强,故承载力越大。经分析,k值每增大1,承载力约提高917 kN。
3.2.2 钢管径厚比对极限承载力的影响 径厚比的影响主要表现在对核心混凝土的约束作用上。径厚比不同,其对混凝土的约束作用就不同,钢管径厚比越大,其对混凝土的约束作用越弱,反之,约束作用越强。以文献[22]中FZ-1柱,采用不同的径厚比,得到的承载力变化如图6所示。
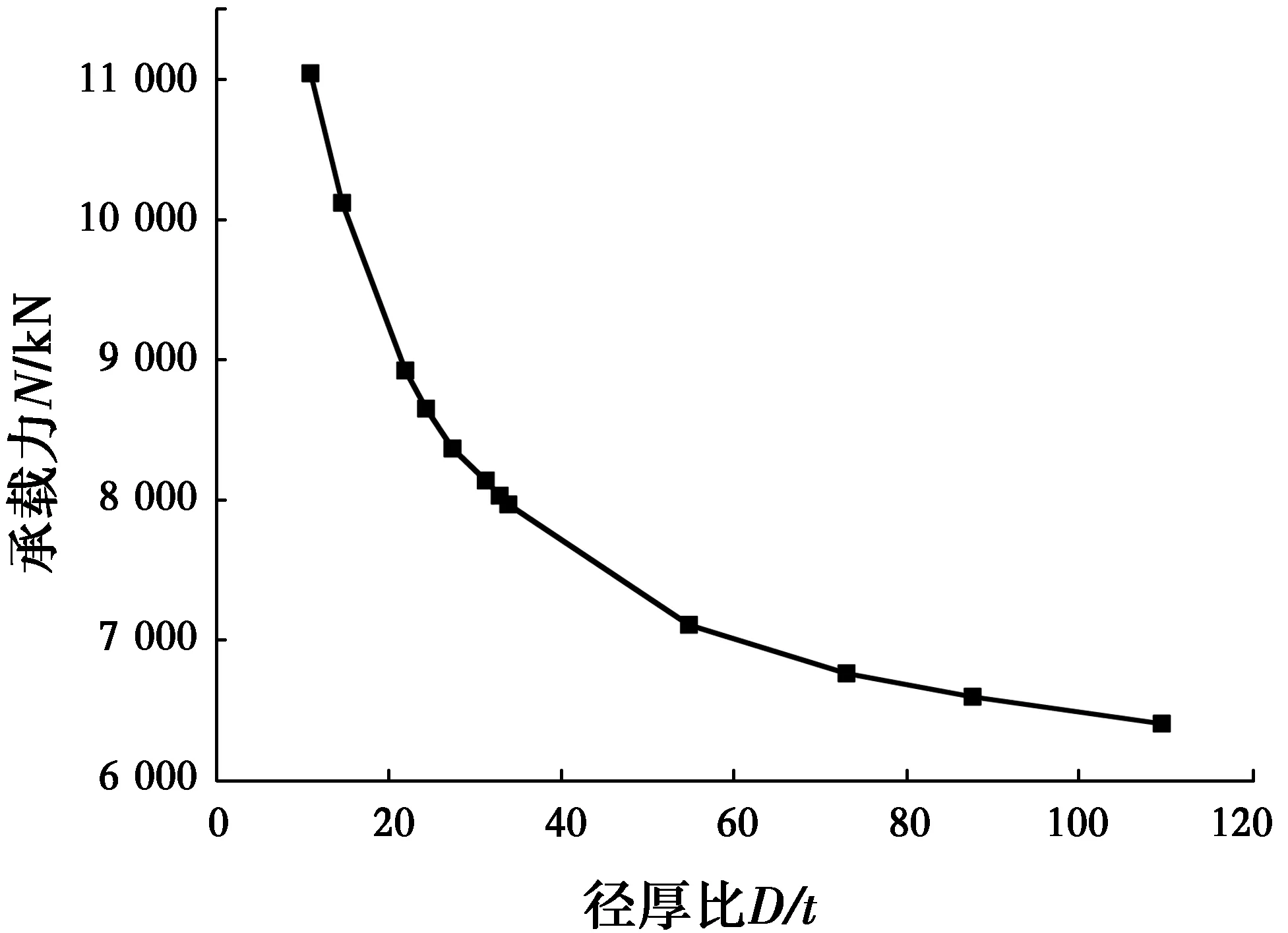
图6 FZ-2柱Nu与径厚比的关系Fig.
由图6可知,随着径厚比的增大,极限承载力逐渐变小,并且减小的速率越来越慢。故为获得较大的承载力,钢管的径厚比不宜过大。
3.2.3 材料拉压比α与中间主应力影响系数b的影响 以文献[22]中试件FZ-2为例进行分析,取α分别为0.8、0.9、1.0,取b分别为0、0.2、0.4、0.6、0.8、1.0进行承载力的计算,如图7所示。
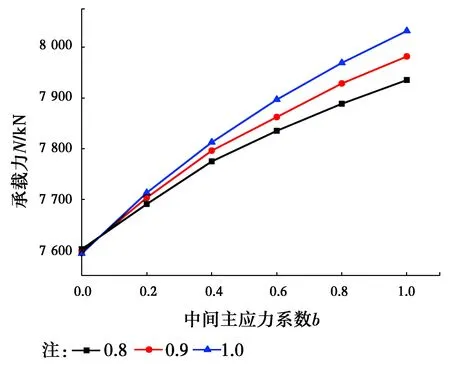
图7 FZ-2柱Nu与b和α的关系Fig.
由图可见,在中间主应力系数b不变的情况下,承载力随着α值的增加而增加;在材料拉压比α不变的情况下,中间主应力系数b越大,承载力越高;而理论上b值越大,极限面也越大,理论与试验分析相吻合。在中间主应力增加量相同的情况下,材料拉压比越大,承载力曲线斜率越大,即承载力增加越多。综上所述,中间主应力和材料拉压比对承载力有影响,故计算时考虑二者对承载力的影响会使结果更加精确。
4 结 论
1)基于双剪统一强度理论,综合考虑了材料拉压比、中间主应力的影响,并且考虑了内部混凝土受到的双重约束作用,推导出了高强钢管混凝土叠合柱轴压承载力的计算公式。该公式能合理的考虑材料的实际性能,又能真实的反应构件各部分的受力状况。通过试验值与本文理论计算值的对比,证明本文推出的方形高强钢管混凝土叠合柱轴压极限承载力计算方法是正确的。
2)通过分析可知:侧压系数越大、中间主应力系数越大,承载力越高;材料拉压比的提高也会使承载力提高;径厚比越大,钢管对混凝土的约束作用越弱,从而导致承载力降低。
[1] 尧国皇, 李永进, 廖飞宇. 钢管混凝土叠合柱轴压性能研究[J]. 建筑结构学报, 2013, 34(5): 114-121.
YAO G H, LI Y J, LIAO F Y. Behavior of concrete-filled steel tube reinforced concrete columns subjected to axial compression [J]. Journal of Building Structures,2013,34(5):114-121. (in Chinese)
[2] 林立岩,李庆刚.钢管混凝土叠合柱的设计概念与技术经济性分析 [J].建筑结构,2008,38(3):17-21.
LIN L Y,LI Q G.Design concept and analysis of technical economy for steel tube-reinforced concrete column [J].Building Structure,2008,38(3):17-21. (in Chinese)
[3] EVIRGEN B,TUNCAN A,TAKIN K.Structural behavior of concrete-filled steel tubular sections under axial compression [J].Thin-Walled Structures,2014,80:46-56.
[4] WANG X D,LIU J P,ZHANG S M.Behavior of short circular tube-reinforced-concrete columns subjected to eccentric compression [J].Engineering Structures,2015,105:77-86.
[5] 吕学涛,杨华,张玉琢,等.高温作用后圆钢管钢筋混凝土轴压短柱力学性能试验研究[J].建筑结构学报,2015,36(2):133-141.
LYU X T,YANG H,ZHANG Y Z,et al.Experimental study on axial mechanical behavior of reinforced concrete-filled circular steel tubular short columns after exposure to high temperatures [J].Journal of Building Structures,2015,36(2):133-141. (in Chinese)
[6] 幸坤涛,赵国藩,岳清瑞.高强钢管混凝土核心柱轴压短柱的承载力研究[J].钢结构,2002,17(57):18-21.
XING K T,ZHAO G F,YUE Q R.Research on bearing capacity of axially compressed short core column with high strength concrete-filled steel tube[J].Steel Construction,2002,17(57):18-21. (in Chinese)
[7] 聂建国,柏宇,李盛勇,等.钢管混凝土核心柱轴压组合性能分析[J].土木工程学报,2005,38(9):9-13.
NIE J G,BAI Y,LI S Y,et al.Analyses on composite column with inside concrete filled tube under axial compression [J].China Civil Engineering Journal,2005,38(9):9-13. (in Chinese)
[8] 龙跃凌,蔡健.核心高强钢骨混凝土组合柱轴压承载力计算新方法[J].华南理工大学学报(自然科学版),2010,38(11):26-31.
LONG Y L,CAI J.A New axial bearing capacity calculation method for composite column with core of high-strength concrete-filled steel tube [J].Journal of South China University of Technology(Natural Science Edition),2010,38(11):26-31. (in Chinese)
[9] 郭全全,李芊,章沛瑶,等.钢管混凝土叠合柱偏心受压承载力的计算方法[J].土木工程学报,2014,47(5):56-63.
GUO Q Q,LI Q,ZHANG P Y,et al.Calculation for bearing capacity of steel tube reinforced concrete columns under eccentric compression [J].China Civil Engineering Journal,2014,47(5):56-63. (in Chinese)
[10] 徐蕾,刘玉彬.钢管混凝土叠合柱耐火性能研究[J].建筑结构学报,2014,35(6):33-41.
XU L,LIU Y B.Research on fire resistance of CFSTRC subjected to fire [J].Journal of Building Structures,2014,35(6):33-41. (in Chinese)
[11] 尧国皇.钢管混凝土叠合柱轴压工作性能研究[D].北京:清华大学,2012.
YAO G H.Research on performance of concrete-filled steel tube reinforced concrete columns [D].Beijing:Tsinghua University,2012. (in Chinese)
[12] MANDER J B,PRIESTLEY M J N,PARK R.Theoretical stress-strain in model for confined concrete [J].Journal of Structural Engineering,1988,114(8):1804-1826.
[13] 俞茂宏.混凝土强度理论及其应用[M].北京:高等教育出版社,2002.
YU M H.Concrete strength theory and its engineering application [M].Beijing:Higher Education Press,2002. (in Chinese)
[14] VARMA A H,SAUSE R,RICLES J M,et al.Development and validation of fiber model for high strength square concrete filled steel tube beam-columns [J].American Concrete Institute Structural Journal,2005,102(1):73-84.
[15] 吴鹏,赵均海,李艳.方钢管混凝土短柱轴压极限承载力研究[J].四川建筑科学研究,2013,39(3):8-13.
WU P,ZHAO J H,LI Y,et al.Study on the axial ultimate bearing capacity of square concrete-filled steel tubular,stub column [J].Sichuan Building Science,2003,39(3):8-13. (in Chinese)
[16] 赵均海.强度理论及其工程应用[M].北京:科学出版社,2003.
ZHAO J H.Strength theory and its engineering application [M].Beijing:Science Press,2003. (in Chinese)
[17] 中国土木工程学会高强与高性能混凝土委员会.高强混凝土结构设计与施工指南[M].2版.北京:中国建筑工业出版社,2001.
China Civil Engineering Society High Strength and High Performance Concrete Committee.High strength concrete structure design and construction guide [M].2 Edition.Beijing:China Building Industry Press,2001. (in Chinese)
[18] 令昀,赵均海,李艳.PBL加劲型方钢管混凝土短柱轴压承载力统一解[J].钢结构,2014,29(10):13-17.
LING Y,ZHAO J H,LI Y.Unified solution of ultimate bearing capacity for concrete-filled steel square tubular short column stiffened with PBL [J].Steel Construction,2014,29(10):13-17. (in Chinese)
[19] 王仁,熊祝华,黄文彬.塑性力学基础[M].北京:科学出版社,1982.
WANG R,XIONG Z H,HUANG W B.Foundation of plastic mecghanics [M].Beijing: Science Press,1982. (in Chinese)
[20] 过镇海,时旭东.钢筋混凝土原理和分析[M].北京:清华大学出版社,2003.
GUO Z H,SHI X D.The principle and analysis of the reinforced concrete [M].Beijing:Tsinghua University Press,2003. (in Chinese)
[21] 谢晓锋.高强钢管(骨)混凝土核心柱轴压性能的试验研究[D].广州:华南理工大学,2002.
XIE X F.An experimental research on the composite column with core of high-strength concrete-filled steel tube under axial compression [D].Guangzhou:South China University of Technology,2002. (in Chinese)
[22] 蔡健,谢晓锋,杨春,等.核心高强钢管混凝土柱轴压性能的实验研究[J].华南理工大学学报(自然科学版),2002,30(6):81-85.
CAI J,XIE X F,YANG C,et al.An experimental research on the composite column with core of high-strength concrete-filled steel tube under axial compression [J].Journal of South China University of Technology(Natural Science Edition),2002,30(6):81-85. (in Chinese)
[23] 李鹏.钢管高强混凝土核心柱受压性能实验与理论研究[D].杭州:浙江大学,2005.
LI P.Experimental and theoretic study on compression characteristics of composite column with core of high-strength concrete filled steel tube [D].Hangzhou:Zhejiang University, 2005. (in Chinese)
(编辑 王秀玲)
National Natural Science Foundation of China(No.41202191,51508028); Science and Technology Public Relations Project of Social Development of Shanxi(No.2015SF272); China Postdoctoral Science Foundation Project(No.2014M562358,2014M562357); Project of Natural Science Foundation Research Project of Shanxi(No.2014JQ7290,2015JM4146); Central University Special Foundation Project on Basic Scientific Research Business of Chang’an Universitry(No.310826161007)
Ultimate bearing capacity of square steel tube-reinforced high strength concrete column under axial compression
Zhao Junhai, Hou Yulin, Zhang Changguang
(School of Civil Engineering, Chang’ an University, Xi’an 710061,P.R.China)
Based on the unified strength theory and the influences of intermediate principal stress and the material of tension and compression ratio were considered when coming down to the ultimate bearing capacity of square steel tube-reinforced high strength concrete column. Effective constraint coefficient and ineffective constraint coefficient were introduced to consider the different constraint functions of concrete derived from the stirrups, the constraint concrete outside steel tube was divided into effective constraint region and ineffective constraint region. The square section was equivalent to circular section to consider the double constraint function to concrete in steel tube derived from steel tube and outer steel reinforced concrete. Then a new method for the axial ultimate bearing capacity of square steel tube-reinforced concrete column was deduced. The results were in good agreement with the experimental results and the correctness of the theory formulae was proved. Influential effects of some parameters were analyzed and the analysis results showed that the ultimate bearing capacity of square steel tube-reinforced high strength concrete column increased with the increase of the side pressure coefficient. Influence coefficient of intermediate principal stress, the material of tension and compression ratio and the longitudinal reinforcement ratio, while it decreases with the increase of radius-thickness ratio.
steel tube-reinforced concrete column;stirrup constraint; strength theory; ultimate bearing capacity
10.11835/j.issn.1674-4764.2016.05.003
2015-11-05
国家自然科学基金(41202191、51508028);陕西省社会发展科技攻关项目(2015SF272);中国博士后科学基金(2014M562358、2014M562357);陕西省自然科学基础研究计划(2014JQ7290、2015JM4146);长安大学中央高校基本科研业务费专项基金(310826161007)
赵均海(1960-),教授,博士生导师,主要从事结构工程和固体力学研究,(E-mail)Zhaojh@chd.edu.cn。
TU312;TU398
A
1674-4764(2016)05-0020-07
Received:2015-11-05
Author brief:Zhao Junhai(1960-),professor,doctoral supervisor,main research interests: structural engineering and solid mechanics, (E-mail)zhaojh@chd.edu.cn.
