GFRP肋式剪力连接件受力性能对比试验研究

黄海林，李遨，祝明桥，郭原草，曾垂军

(湖南科技大学 土木工程学院，湖南 湘潭 411201)



GFRP肋式剪力连接件受力性能对比试验研究

黄海林，李遨，祝明桥，郭原草，曾垂军

(湖南科技大学 土木工程学院，湖南 湘潭 411201)

组合结构；肋式剪力连接件；推出试验；破坏机理；粘结滑移

界面滑移是影响GFRP混凝土组合梁/板受力性能的重要因素。实际工程中，可在GFRP混凝土组合梁/板的界面增设剪力连接件保证GFRP与混凝土的协同工作，目前常用的方法有界面喷砂、粘贴GFRP剪力连接件[8]、预埋栓钉[9]以及采用膨胀剂连接等。其中，以粘贴GFRP剪力连接件和预埋栓钉的方法最为可靠，为此，GB 50608—2010《纤维增强复合材料建设工程应用技术规范》规定：GFRP混凝土组合梁的界面应粘贴树脂混凝土条、GFRP波形板、GFRP小工字梁等有效的剪力连接件保证界面可靠连接。为改善下部GFRP构件与上部混凝土的界面粘结性能，Kubo等[10]、Cho等[11]、Bank等[8, 12]、Fam等[5]、Keller等[13]、杨勇等[14]、黄辉等[15]、薛伟辰等[16]，分别借助不同构造做法各自开发了GFRP混凝土组合桥面板，其共同点在于：在GFRP底模上增设GFRP板肋，伸出的板肋兼作为剪力连接件。

围绕GRRP混凝土组合梁/板中剪力连接件的力学性能，国内外学者进行了初步探索，主要有：Nguyen等[17]通过在GFRP工字形构件上预埋抗剪栓钉，进行了采用栓钉的GFRP超高性能纤维改性混凝土界面推出试验研究；薛伟辰等[16]、Nam等[18]也分别对开孔板GFRP剪力连接件进行了推出试验研究。以上推出试验研究为GFRP剪力连接件的工程应用提供了理论依据，但主要集中在栓钉和矩形开孔板两种形式。为此，笔者提出一种增设有T形肋或矩形肋剪力连接件的GFRP空心箱形构件，如图1所示。整个GFRP空心箱形构件通过拉挤工艺一次成型，能很好的保证伸出的剪力连接件与下部空心箱形构件形成整体共同受力，并通过对比试验重点研究了肋内开孔及肋的截面形式对GFRP肋式剪力连接件受力性能的影响。

图1 GFRP空心箱形构件Fig.1 GFRP hollow box

1 推出试件设计与制作

1.1 推出试件设计

参考欧洲规范4设计了3组共8个GFRP肋式剪力连接件，包括矩形肋开孔、T形肋开孔以及T形肋不开孔3组GFRP肋式剪力连接件，编号分别为JK1～JK2、TK1～TK3及T1～T3。每个推出试件由中间GFRP空心箱形构件与左右两边混凝土块组成。推出试件设计见图2。推出试件GFRP材性参数见表1，混凝土立方体抗压强度实测平均值为31.2 MPa。

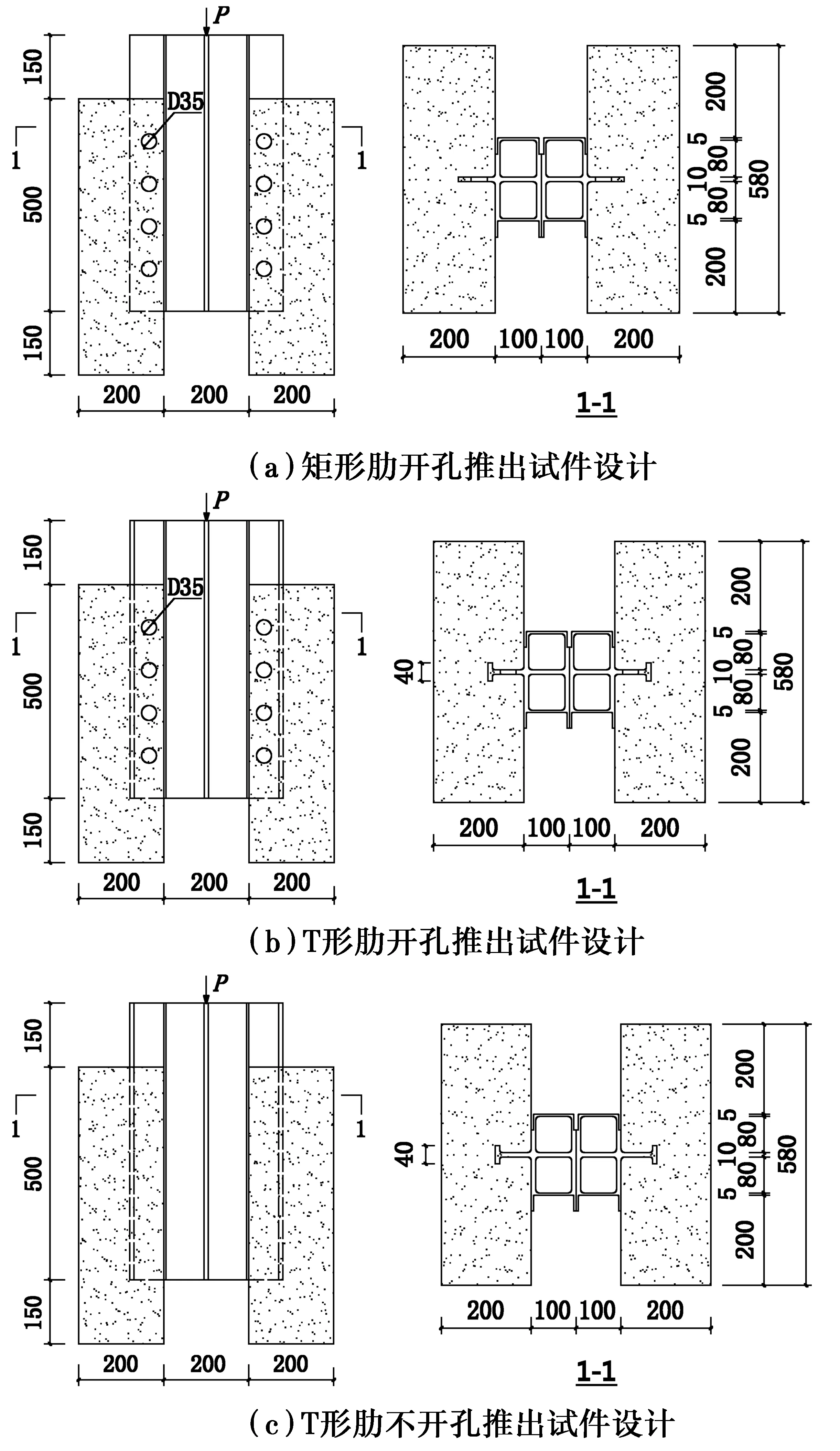
图2 推出试件设计Fig.2 Push-out specimens

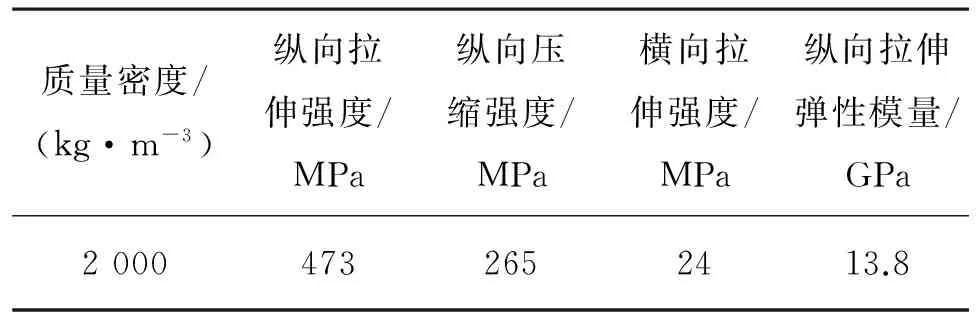
质量密度/(kg·m-3)纵向拉伸强度/MPa纵向压缩强度/MPa横向拉伸强度/MPa纵向拉伸弹性模量/GPa20004732652413.8

1.2 推出试件制作

推出试件的中间GFRP空心箱形构件由两个增设有剪力连接件的GFRP箱型构件，通过粘接组合成型。粘贴步骤：首先，用砂纸打磨GFRP表面，打磨方向呈45°；随后，清理表面的灰尘并用酒精洗净；在GFRP粘贴面上抹结构胶并对中按压；最后，养护7 d，成型后的中间GFRP构件见图3。为避免加载时顶端GFRP上的局压应力过大而导致局压破坏，在顶端空心箱中用混凝土灌实，灌实长度为150 mm。

图3 拼接成型后的中间GFRP空心箱形构件Fig.3 GFRP hollow box components after

2 试验装置、加载方案及测点布置

试验用主要设备有：大刚度反力门架、250 t千斤顶、JMZX智能振弦实心荷载传感器、DH3816静态应变测试分析系统以及百分表。试验装置见图4。

图4 试验装置Fig.

加载分预加载和正式加载两阶段。预加载时每级荷载取10 kN，荷载上限取0.1倍计算极限荷载；正式加载分2个控制阶段，开裂前采用力控制加载，每级荷载取计算极限荷载的1/20，开裂后改由位移控制加载，每级位移加载取0.2 mm。

为测量GFRP肋式剪力连接件的应变变化规律，在矩形肋、T形肋以及GFRP空心箱的侧壁上布置应变片，应变测点布置见图5。

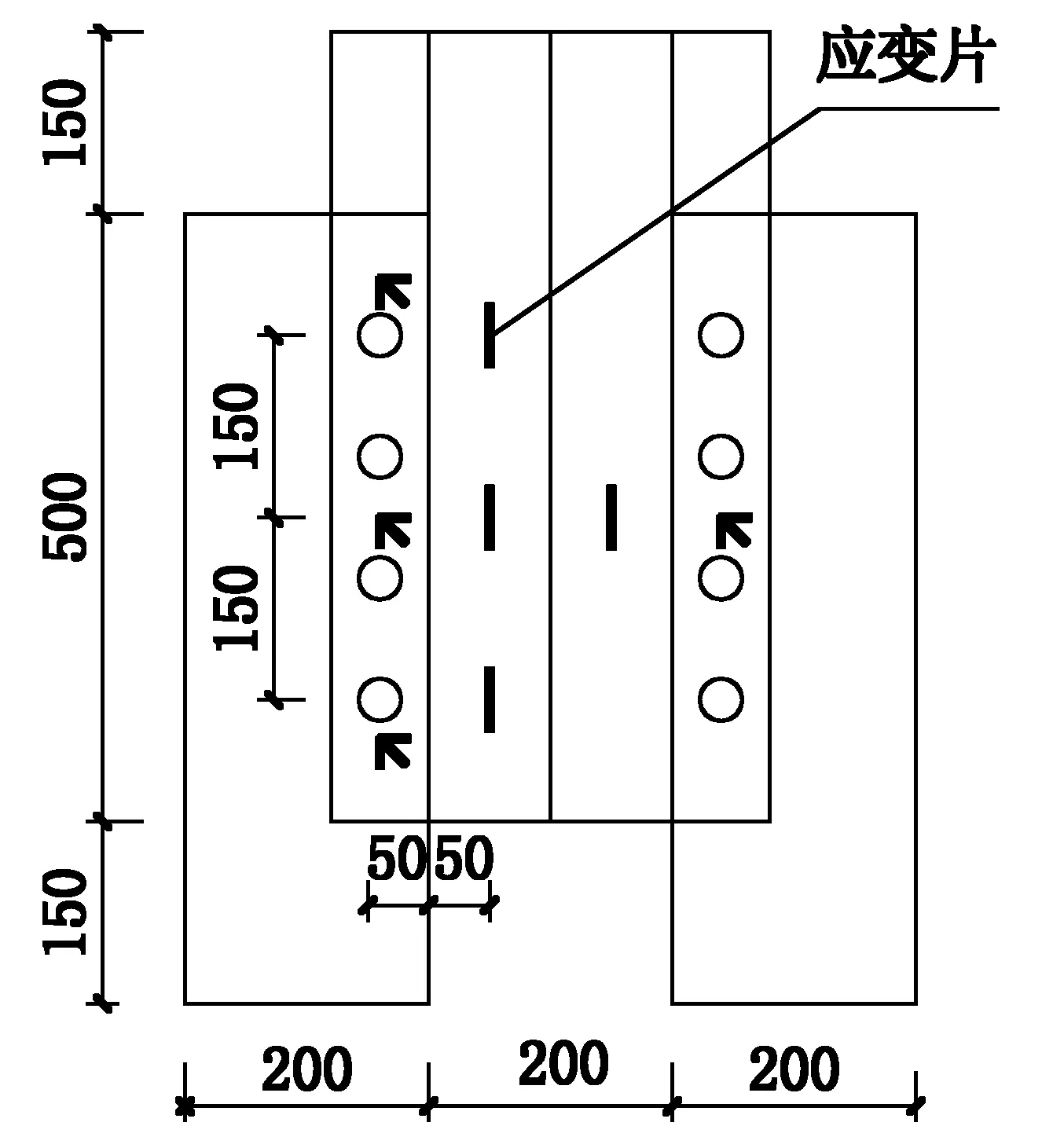
图5 应变片布置示意图Fig.5 Strain gauge

为测量GFRP与混凝土粘贴界面的竖向滑移和混凝土块的水平侧移，分别布置了2个百分表，布置示意如图6所示。

图6 百分表布置示意图Fig.6 Displacement transducer

3 试验结果及分析

3组试件的主要试验结果见表2。其中，pu为极限承载力、su为极限承载力对应的滑移量。

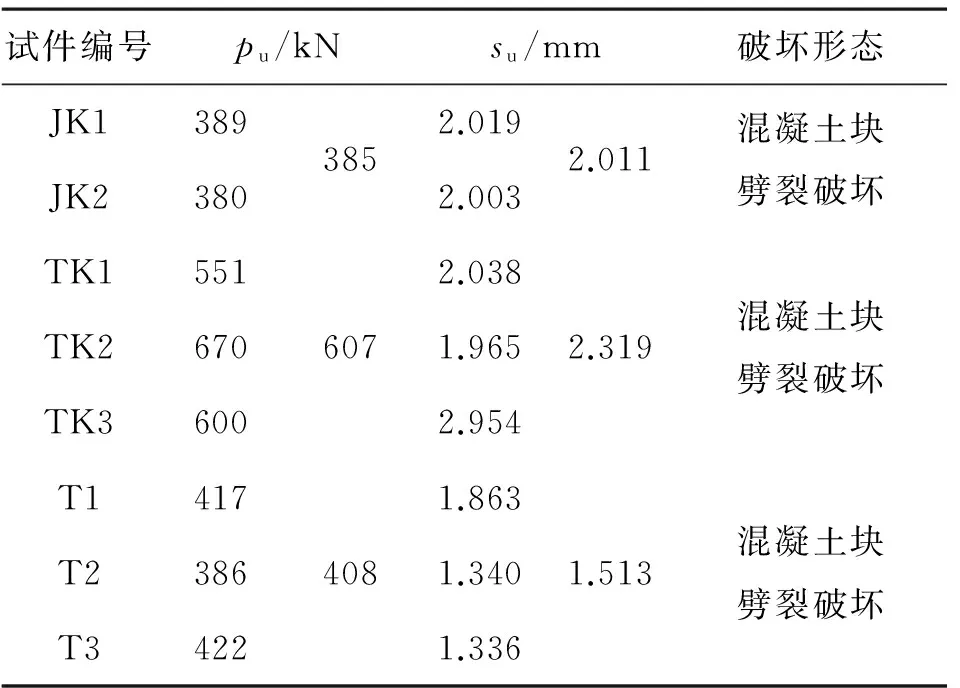
表2 推出试验结果Table 2 Test results

3.1 试验过程及破坏形态

1)两类GFRP肋式剪力连接件受力全过程

矩形肋开孔试件JK1～JK2：两个试件表现出基本相同的受力性能，下面,仅以试件JK1为代表来说明本组试件从开始加载到最终破坏的受力全过程。开裂前荷载稳定上升，滑移变化较小。354 kN时，左右两边混凝土块顶面沿矩形肋端部边缘突然出现45°角斜主裂缝；继续加载，左右两边混凝土块内表面底部同时出现人字形劈裂缝，该裂缝始于底部矩形肋最外边缘并同时向两侧呈人字形延伸，左右两边混凝土块外表面顶部出现一些细小的竖向劈裂缝、且不断向下延伸；389 kN时，两边混凝土块出现劈裂破坏，破坏始于两边混凝土块顶面的斜主裂缝迅速扩展，破坏时GFRP肋式剪力连接件基本完整。典型破坏形态及裂缝分布见图7。

图7 矩形肋试件典型破坏形态及裂缝分布图Fig.7 Typical failure pattern and crack

图8 T形肋试件典型破坏形态及裂缝分布图Fig.8 Typical failure pattern and crack

2)肋内开孔对试件受力性能的影响

T形肋不开孔试件T1～T3呈现出与T形肋开孔试件TK1～TK3基本相同的受力性能，其最终破坏形态与裂缝分布机理相同，最终左右两边混凝土块出现劈裂破坏，破坏始于混凝土块内表面底部的八字形劈裂主裂缝，破坏时GFRP肋式剪力连接件基本完整；区别在于T形肋开孔后，孔内混凝土榫产生的销栓效应明显提高了试件的极限承载力，改善了试件的抗剪延性，对比表2可知，T形肋开孔后，平均强度提高48.8%，极限强度对应的平均滑移增大53.3%。可见，T形肋开孔后，能显著改善GFRP肋式剪力连接件的受力性能，但不能改变其最终破坏形态。

3)肋的截面形式对试件受力性能的影响

对比矩形肋开孔试件JK1～JK2与T形肋开孔试件TK1～TK3，可以发现：两者开孔形式相同，肋的截面形式不同，T形肋明显增大了GFRP与混凝土的接触面积；尽管最终破坏时两类试件均为混凝土劈裂破坏，但破坏时起控制的主裂缝不同，矩形肋开孔试件破坏始于左右两边混凝土块顶面的斜主裂缝迅速扩展，而T形肋开孔试件破坏始于混凝土块内表面底部八字形劈裂主裂缝迅速扩展。根据表2，对比矩形肋开孔试件的平均强度，T形肋不开孔试件、T形肋开孔试件分别高出6.0%、57.7%，可见肋的截面形式对试件承载力的影响要远大于孔内混凝土榫对试件承载力的影响，因此，实际工程中若需要较高的抗剪强度，建议首先采用T形肋，其次可在肋内开孔；对比T形肋开孔试件极限强度对应的平均滑移，矩形肋开孔试件小13.3%，可见T形肋比矩形肋试件的延性要好。

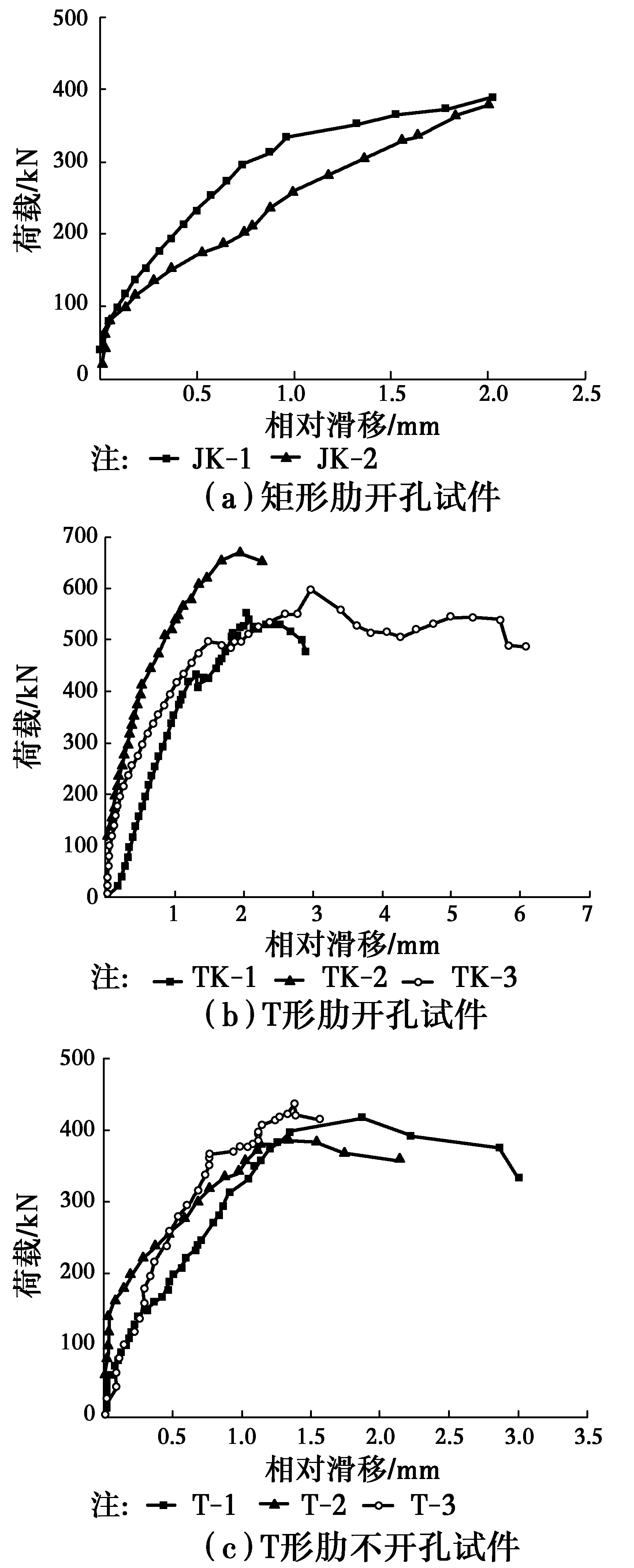
图9 荷载滑移曲线Fig.9 Load versus slip curves

3.3 GFRP肋式剪力连接件轴向压应变变化规律

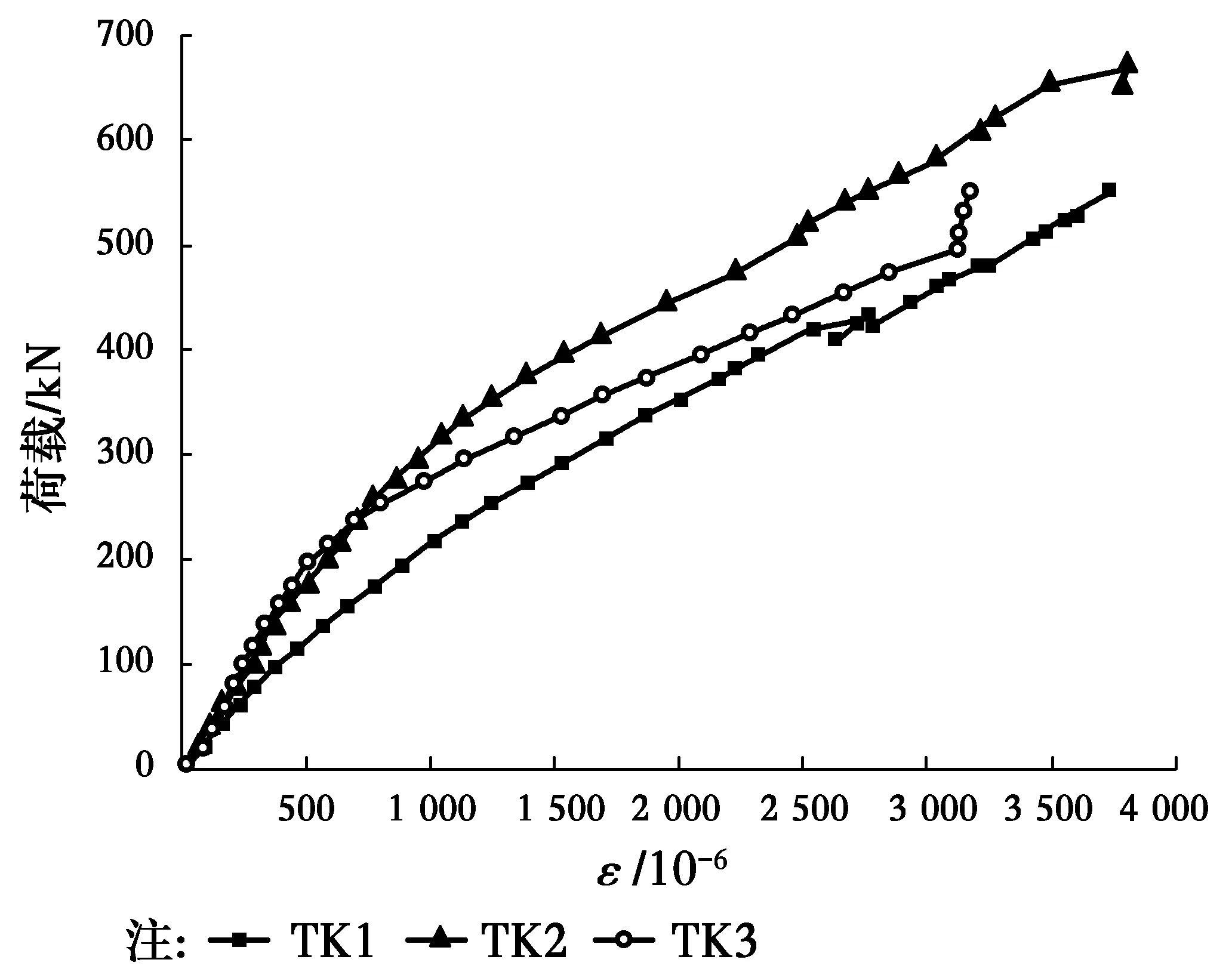
图10 GFRP肋式剪力连接件肋上 荷载轴向压应变曲线Fig.10 Load versus strain curves in the ribs

3.4 GFRP空心箱体侧壁轴向压应变变化规律

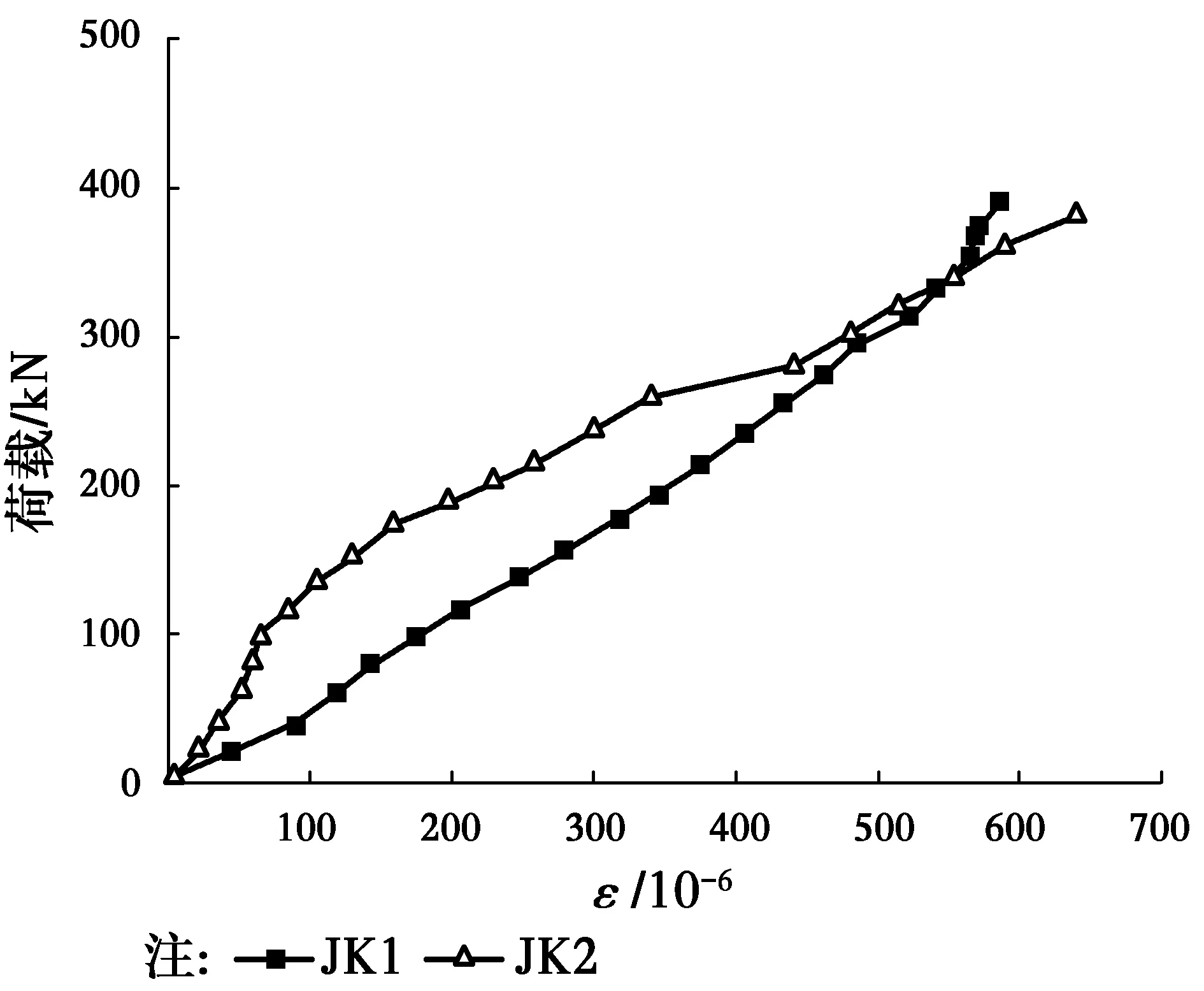
图11 GFRP空心箱体侧壁 荷载轴向压应变曲线Fig.11 Load versus strain curves in the GFRP

4 GFRP肋式剪力连接件受力性能计算

4.1 GFRP肋式剪力连接件极限承载力计算公式

基于以上试验研究结果可知，两类GFRP肋式剪力连接件最终破坏均由混凝土劈裂破坏控制，GFRP肋式剪力连接件基本完整，影响GFRP肋式剪力连接件极限承载力的主要因素有：1)左右两边混凝土块的强度；2)GFRP肋式剪力连接件中肋的截面形式，主要包括矩形肋和T形肋两种情况；3)肋内孔洞内混凝土榫提供的销栓力。GFRP肋式剪力连接件极限承载力Vu计算公式为

(1)

(2)

(3)

式(1)中:Vc1为混凝土榫所提供的抗剪销栓力，按式(2)进行计算；Vc2为左右两边混凝土块所提供的强度，按式(3)进行计算。需要说明的是，对于T形不开孔试件，其极限承载力仅取决于左右两边混凝土块的强度，故式(1)应改为Vu=Vc2。

式(2)中:n1为混凝土榫的数目；α1为孔洞截面系数，对于圆孔可取1.0；α2为剪力连接件截面形状系数，T形肋剪力连接件建议取1.2，矩形剪力连接件建议取1.0；Ac为单个孔洞截面面积；ft混凝土轴心抗拉强度设计值。

式(3)中:n2为混凝土块的数目，取2.0；η为两边混凝土块共同受力均匀系数，取值不超过1.0，主要表明两边混凝土块共同受力的均匀度，本文中取1.0；b为混凝土块厚度；h为混凝土块高度；αb、αh分别为与混凝土块厚度b、高度h有关的承载力折减系数，取值不超过1.0，主要反映混凝土块参与受力面的面积大小，本文中T形肋试件αb与αh均取1.0，矩形肋试件αb与αh分别取0.88和1.0。

根据式(1)～(3)计算的GFRP肋式剪力连接件承载力计算值与试验值对比结果见表3。由表3可知，对于矩形肋开孔试件与T形肋不开孔试件，按本文公式计算的极限承载力与试验值吻合很好；对于T形肋开孔试件，按本文公式计算的极限承载力具备较高的安全储备。

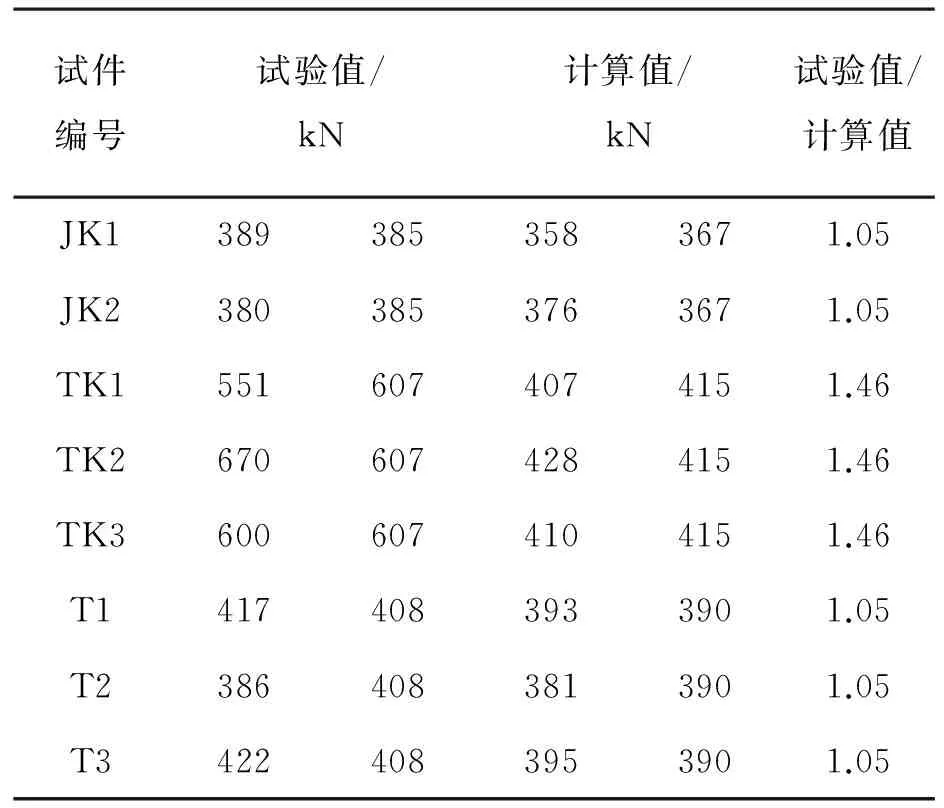
表3 GFRP肋式剪力连接件承载力 试验值与计算值对比结果Table 3 Comparison of ultimate shearing capabilitybetween test value and calculated value

4.2 抗剪刚度计算公式

(4)

式中：s表示界面滑移，p为承载力；pu为GFRP肋式剪力连接件的极限承载力；α、β的取值与肋内开孔情况、肋的截面形式相关，其取值为

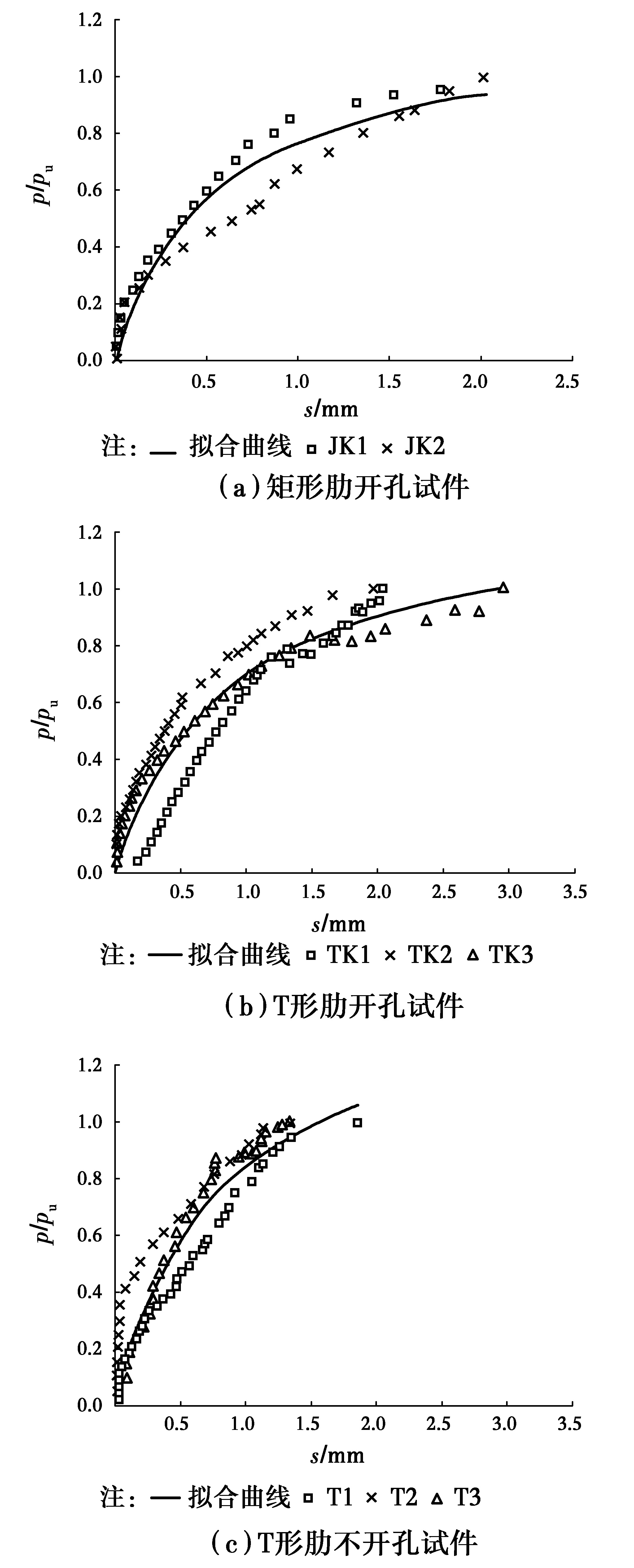
图12 荷载滑移拟合曲线Fig.12 Load versus slip fitting

矩形肋开孔试件：α=0.468，β=0.830

T形肋开孔试件：α=0.668，β=0.770

T形肋不开孔试件：α=0.509，β=0.661

(5)

式中：pu为GFRP肋式剪力连接件的极限承载力；s0.4pu为荷载达到0.4pu时所对应的滑移量。

将p=0.4pu代入式(4)，得

(6)

故最终抗剪刚度K为

(7)

5 结 论

通过3组共8个GFRP肋式剪力连接件的推出试验，重点研究肋内开孔及肋的截面形式对GFRP肋式剪力连接件受力性能的影响，其结论如下：

1)所有试件均呈相同的破坏机理，最终破坏时混凝土出现劈裂破坏，GFRP肋式剪力连接件基本完整。

2)对比矩形肋开孔GFRP肋式剪力连接件，T形肋开孔GFRP肋式剪力连接件能提供更高的抗剪强度以及更好的抗剪延性；对比T形肋不开孔剪力连接件，肋内开孔后，T形肋开孔GFRP肋式剪力连接件能提供更高的抗剪强度以及更好的抗剪延性。

3)基于试验得到的破坏机理，建立了考虑肋内开孔情况及肋截面形式影响的GFRP肋式剪力连接件极限承载力计算公式。

[1] TENG J G，YU T，FERNANDO D. Strengthening of steel structures with fiber-reinforced polymer composites [J]. Journal of Constructional Steel Research，2012，78(6): 131-143.

[2] ZHAO X L，ZHAO L. State-of-the-art review on FRP strengthened steel structures[J]. Engineering Structures，2007，29(8): 1808-1823.

[3] HOLLAWAY L C. A review of the present and future utilisation of FRP composites in the civil infrastructure with reference to their important in-service properties[J]. Construction and Building Materials，2010，24(12): 2419-2445.

[4] BAKIS C E，BANK L C，BROWN V L，et al. Fiber-reinforced polymer composites for construction-state-of-the-art review[J]. Journal of Composites for Construction，2002，6(2):73-87.

[5] NELSON M，FAM A. Full bridge testing at scale constructed with novel FRP stay-in-place structural forms for concrete deck [J]. Construction and Building Materials，2014，50(2): 368-376.

[6] 冯鹏. 复合材料在土木工程中的发展与应用[J]. 玻璃钢/复合材料，2014(9): 99-104.

FENG P. Development and application of composite in civil engineering[J]. Fiber Reinforced Plastics/Composites，2014(9): 99-104. (in Chinese)

[7] NAM J H，YOON S J，MOON H D，et al. Development of FRP-concrete composite bridge deck in Korea state-of-the-art review [J]. Key Engineering Materials，2006，236-328: 1715-1718.

[8] HANUS J P，BANK L C，OLIVA M G. Combined loading of a bridge deck reinforced with a structural FRP stay-in-place form[J]. Construction and Building Materials，2009，23(4): 1605-1619.

[9] CORREIA J R，BRANCO F A，FERREIRA J. GFRP-concrete hybrid cross-sections for floors of buildings[J]. Engineering Structures，2009，31(6): 1331-1343.

[10] MATSUI S，ISHIZAKI S，KUBO K. An experimental study on durability of FRP-RC composite deck slabs of highway bridges[C]// 3rd Int. Conf. on Concrete Under Severe Conditions: Environment & Loading. Vancouver，Canada: CONSEC'01，2001：933-940.

[11] CHO K，PARK S，KIM S，et al. Shear connection system and performance evaluation of FRP-concrete composite deck [J]. KSCE Journal of Civil Engineering，2010，14(6): 855-865.

[12] BANK L C，OLIVA M G，BAE H，et al. Pultruded FRP plank as formwork and reinforcement for concrete members[J]. Advances in Structural Engineering，2007，10(5): 525-535.

[13] KELLER T，SCHAUMANN E，VALLEE T. Flexural behavior of a hybrid FRP and lightweight concrete sandwich bridge deck [J]. Composites Part A: Applied Science and Manufacturing，2007，38(3): 879-889.

[14] 杨勇，刘玉擎，范海丰. FRP-混凝土组合桥面板疲劳性能试验研究[J]. 工程力学，2011，28(6): 66-73.

YANG Y，LIU Y Q，FAN H F. Experimental study on the fatigue behavior of FRP-concrete composite decks[J].Engineering Mechanics，2011，28(6): 66-73. (in Chinese)

[15] 黄辉，王文炜，戴建国. 两跨连续GFRP-混凝土空心组合板受力性能试验研究[J]. 建筑结构学报，2015，36(10): 59-65.

HUANG H，WANG W W，DAI J G. Experimental study on structural performance of two-span continuous GFRP-concrete composite hollow slabs[J].Journal of Building Structures，2015，36(10): 59-65. (in Chinese)

[16] 薛伟辰，张赛，葛畅. FRP混凝土组合梁抗剪连接件试验研究[J]. 公路交通科技(应用技术版)，2014，109(1): 207-210.

XUE W C，ZHANG S，GE C. Experimental study of shear connector in FRP-concrete composite beam[J]. Highway Traffic Technology (Application Technology)，2014，109(1): 207-210. (in Chinese)

[17] NGUYEN H，MUTSUYOSHI H，ZATAR W. Push-out tests for shear connections between UHPFRC slabs and FRP girder[J]. Composite Structures，2014，118: 528-547.

[18] NAM J，YOON S，OK D，et al. Perforated FRP shear connector for the FRP-concrete composite bridge deck[J]. Key Engineering Materials，2007，334/335: 381-384.

(编辑 王秀玲)

National Natural Science Foundation of China(No.51308207，No.51378202)；Project of Hunan Province Education Office (No. 14C0439).

Comparative analysis of push-out tests for two kinds of GFRP shear connectors

Huang Hailin,Li Ao,Zhu Mingqiao,Guo Yuancao,Zeng Chuijun

(College of Civil Engineering, Hunan University of Science and Technology,Xiangtan 411201,Huan,P.R.China)

Shear connectors are the important detailings affecting the mechanical properties of GFRP-concrete composite beams/decks. Rectangular rib and T-type rib GFRP shear connectors are put forward to improve the interfacial bond properties between GFRP and concrete. Eight push-out tests are conducted to evaluate the mechanical behaviors of two rectangular perforated rib GFRP shear connectors and three T-type perforated rib GFRP shear connectors, as well as three T-type rib GFRP shear connectors. The failure patterns, ultimate bearing capacities, load-slip behaviors and load-strain regularities are obtained by contrast tests. Results show that T-type perforated rib GFRP shear connectors show higher strength and better ductility than rectangular perforated rib GFRP shear connectors, and T-type perforated rib GFRP shear connectors show higher strength and better ductility than T-type rib GFRP shear connectors. An empirical equation to predict the ultimate shear resistance is proposed and validated by the experimental data. Idealized load-lip models and equations to predict the load versus slip relationship for all specimens are proposed. Curve fittings are performed to find fitting parameters for all tested specimens and the results show a very good correlation with those of the experiments. An empirical equation to predict the shear rigidity is proposed.

composite structure; shear connector; push-out test; failure mechanism; bond-slip behavior

10.11835/j.issn.1674-4764.2016.05.005

2015-12-02

国家自然科学基金(51308207、51378202)；湖南省教育厅项目(14C0439)

黄海林(1984-)，男，博士，主要从事组合结构及新材料应用研究，(E-mail)hhlvsgenius@163.com。

U443; TU398

A

1674-4764(2016)05-0034-09

Received:2015-12-02

Author brief：Huang Hailin(1984-)，PhD，main research interests:composite structure and application of new materials,(E-mail)hhlvsgenius@163.com.