近爆作用下压型钢板组合楼板动力响应及影响因素数值分析

张秀华，高珊，吴建

(1.东北林业大学 土木工程学院，哈尔滨 150040；2.江苏省结构工程重点实验室，江苏 苏州 215011)



近爆作用下压型钢板组合楼板动力响应及影响因素数值分析

张秀华1,2，高珊1，吴建1

(1.东北林业大学 土木工程学院，哈尔滨 150040；2.江苏省结构工程重点实验室，江苏 苏州 215011)

利用有限元软件ANSYS/LS-DYNA，采用流固耦合的计算方法，对压型钢板组合楼板在近爆炸荷载作用下进行了不同工况的数值模拟，得出其受力形态，分析其动力响应及破坏过程，找出影响楼板动力响应的主要因素。数值分析结果表明：适当增加混凝土厚度和提高压型钢板强度，可以显著降低组合楼板的跨中最大位移，提高组合楼板的延性和抗爆性能；组合楼板中钢筋间距的变化，对组合楼板抗爆性能影响较小。

爆炸荷载；组合楼板；动力响应；影响因素；数值分析

1 有限元数值模型建立

1.1 计算模型

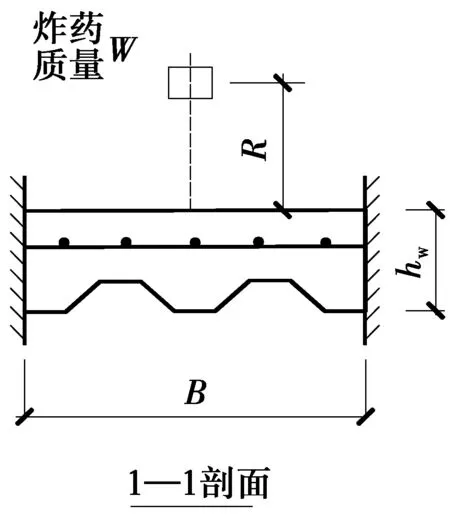
图1 计算模型图Fig.1 Calculation

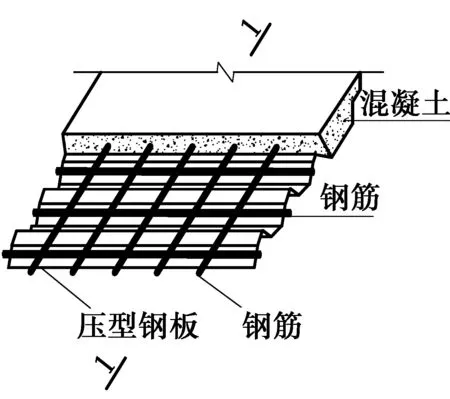
图2 细部剖面图Fig.2 Details cross- sectional

1.2 材料模型

材料模型及相关参数的选取对数值模拟结果的准确性起着决定性作用。在数值计算时，只需在LS-DYNA程序中选择合适材料模型和状态方程，并定义相关参数。文献[15]是选取材料模型的依据，文献[16-19]采用数值模拟和试验相结合的方法，验证其材料参数的可行性与准确性。

TNT炸药采用MAT_HIGH_EXPLOSION_BURN模型来描述应力和应变关系，采用JWJ状态方程来描述压力和体积变形关系[15]，方程为

(1)

式中：A、B、R1、R2、ω为与炸药类型有关的材料常数。材料的具体参数见表1[16]。

数值分析时，不考虑温度的影响，压型钢板和钢筋的材料模型采用LS-DYNA 中的MAT_PLASTIC_KINEMATIC塑性随动强化模型和Mises屈服准则[15]，该模型很好地描述了钢材的弹塑性性能。并通过Cowper-Symonds模型来考虑应变率效应[16]，其动力屈服强度为

(2)

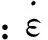
在非线性有限元软件ANSYS/LS-DYNA中，等效塑性应变是用来确定材料经强化后屈服面位置的物理量，是评价材料是否进入塑性的指标。等效塑性应变按下式计算

(3)

式中：εij为等效塑性应变分量(j= 1、2、3)。

压型钢板和钢筋材料参数见表2[16-17]。在数值计算时，当单元的最大应变达到失效应变时，即认为单元失效。由于材料的失效应变与有限元模型的单元尺寸及应变率等因素有关，关于其取值目前还没有统一认识。根据文献[16-17]，钢材的失效应变中取0.12。

空气采用MAT_NULL材料模型和线性多项式状态方程EOS_LINEAR_POLYNOMIAL[15]

(4)

式中：μ=ρ0-1；ρ为当前密度；ρ0为初始密度；E0为单位体积内能。材料参数见表3[16、18]。

表1 TNT炸药模型材料参数Table 1 Explosive material model parameters

表2 钢板及钢筋模型材料参数Table 2 Steel and Reinforced model material parameters

表3 空气模型材料参数Table 3 Air model material parameters

数值分析时，不考虑温度的影响，混凝土采用MAT_HOLMGUIST_JOHNSON_CONCRETE(HJC)本构模型[15]，模型综合考虑了大应变、高应变率、高压效应。用等效强度取代静态屈服强度用以判别和计算结构屈服破坏，用损伤度来判别和计算积累损伤破坏。HJC模型的本构方程为

(5)

(6)

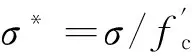
HJC方程可以体现混凝土压力和体积之间的关系，压缩、拉伸阶段和体积关系为

当0<μ<μcrush时为弹性区

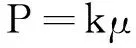
(7)

当μcrush<μ≤μlock时为压碎区

(8)

(9)

当μ≥μlock时为压实区

(10)

式中：k为混凝土单元弹性模量；k1、k2、k3为压力常数；μ为单元体积应变；Pcrush为在μcrush下的单元静水压力；μcrush为压溃点体积应变；Plock为μlock下的单元内净水压力；μlock为压实点体积应变。

材料参数见表4。具体参数在文献[16，18-19]中已经得到应用，并验证材料参数取值的可靠性和准确性。

表4 混凝土模型材料参数Table 4 Concrete model material parameters

1.3 有限元模型

压型钢板混凝土组合楼板采用分离式建模，混凝土、钢筋、钢板单元共用节点，混凝土采用实体单元Solid164，钢筋采用三维梁单元Beam161，钢板采用壳单元Shell163，空气和炸药采用连续介质独立模型，采用实体单元Solid164，采用多物质ALE算法，空气域边界采用无反射边界条件。组合楼板与空气之间采用流固耦合算法。与文献[16]模拟爆炸作用下混凝土梁的研究采用相同算法、单元、边界条件。文献[20]基于Euler算法分析爆炸冲击波在空气中的传播规律，比较不同网格尺寸划分情况且与经验公式对比分析，验证了所采用建模方法的可行性，以及单元类型和网格尺寸的合理性。因此，空气和炸药采用Euler网格划分，单元尺寸均为50 mm；混凝土、钢筋和钢板采用Lagrange网格划分，单元尺寸均为20 mm。有限元划分网格模型如图3所示。

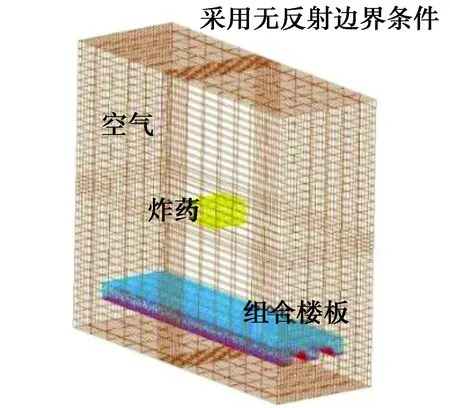
图3 有限元划分网格模型图Fig.3 Finite element mesh

2 爆炸荷载作用下组合楼板动力响应及破坏过程分析

数值计算时，取板跨L=3 m、宽度为B=0.6 m两端简支的单向板为研究对象。TNT炸药距板正上方的距离R=1 m，尺寸200 mm×200 mm×400 mm，等效TNT当量为52.16 kg，即比例距离Z=0.27 m/kg1/3。钢筋HPB300，压型钢板Q345。钢筋间距采用φ10@250，混凝土采用C50。考虑组合楼板实际工作情况，在计算时考虑了楼板自重及楼面活荷载。按《建筑结构荷载规范》(GB 50009—2012)计算出此组合楼板的竖向荷载为6.3 kN/m2。

2.1 爆炸冲击波的传播规律

爆炸冲击波的传播规律如图4所示。图4(a)表明炸药在空气中爆炸产生空气冲击波，爆炸周围瞬间形成高压高温区，气体以起爆点为中心向四周传播；图4(b)表明空气冲击波从爆心开始以球形的波面形式向四周传播，范围扩大；图4(c)、(d)表明当空气冲击波遇到板后发生反射及绕射现象，空气冲击波压力向外分布，一部分能量扩散在空气中，另一部分能量集中在板跨部位，随后逐渐向四周传递能量，此结论与文献[16]的结论吻合，表明采用的分析方法可行。

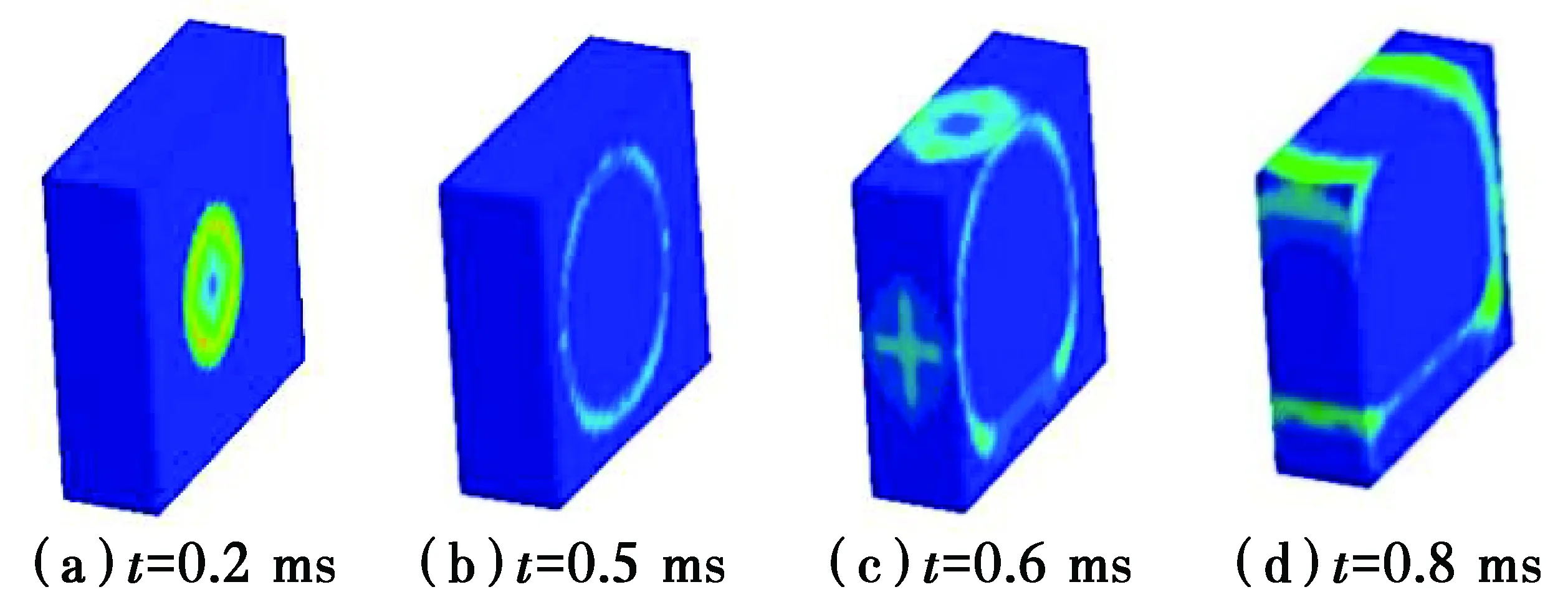
图4 不同时刻冲击波压力云图Fig.4 Different time pressure cloud of shock

2.2 压型钢板组合楼板的动力响应

组合楼板各个构件的破坏情况如图5、图6所示。从图5(a)可以看出，作用时间为0.2 ms时，组合楼板受到爆炸荷载后，炸药正下方的混凝土等效应力较大，向四周逐渐减小。从图5(b)可以看出，作用时间为0.6 ms时，板顶跨中少量混凝土被压碎破坏。从图5(c)、(d)可以看出，跨中和支座附近的混凝土等效应力较大，随着时间变化，板面混凝土破坏范围逐渐增大，板中部混凝土逐渐向四周破坏，支座处混凝土逐渐沿长度方向扩展破坏。

图6(a)、(b)给出了1 ms时刻钢板、钢筋的变形情况。从图6可以看出，当爆炸作用时间为1 ms时，钢板和钢筋跨中部分产生较大的变形。

图6 钢板、钢筋的变形Fig.6 Failure of steel plate and

图7给出了各构件动力响应的测点位置。

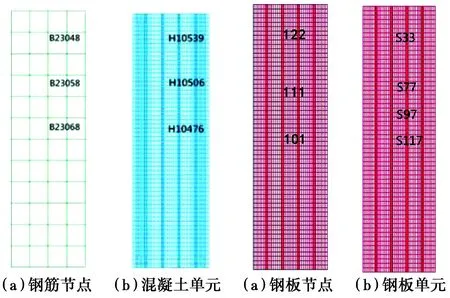
图7 测点位置Fig.7 Measuring

图8给出了不同钢筋单元等效应力时程曲线。从图8可以看出，在受到爆炸荷载作用时，中间和边缘钢筋的等效应力急速上升，超过屈服应力，然后趋于平稳。跨中23068单元受力较大，靠近支座处23058、23048单元受力较小，由于钢材在动力荷载作用下动力效应增大，屈服强度提高，钢筋未被拉断，表明钢筋已进入弹塑性阶段。

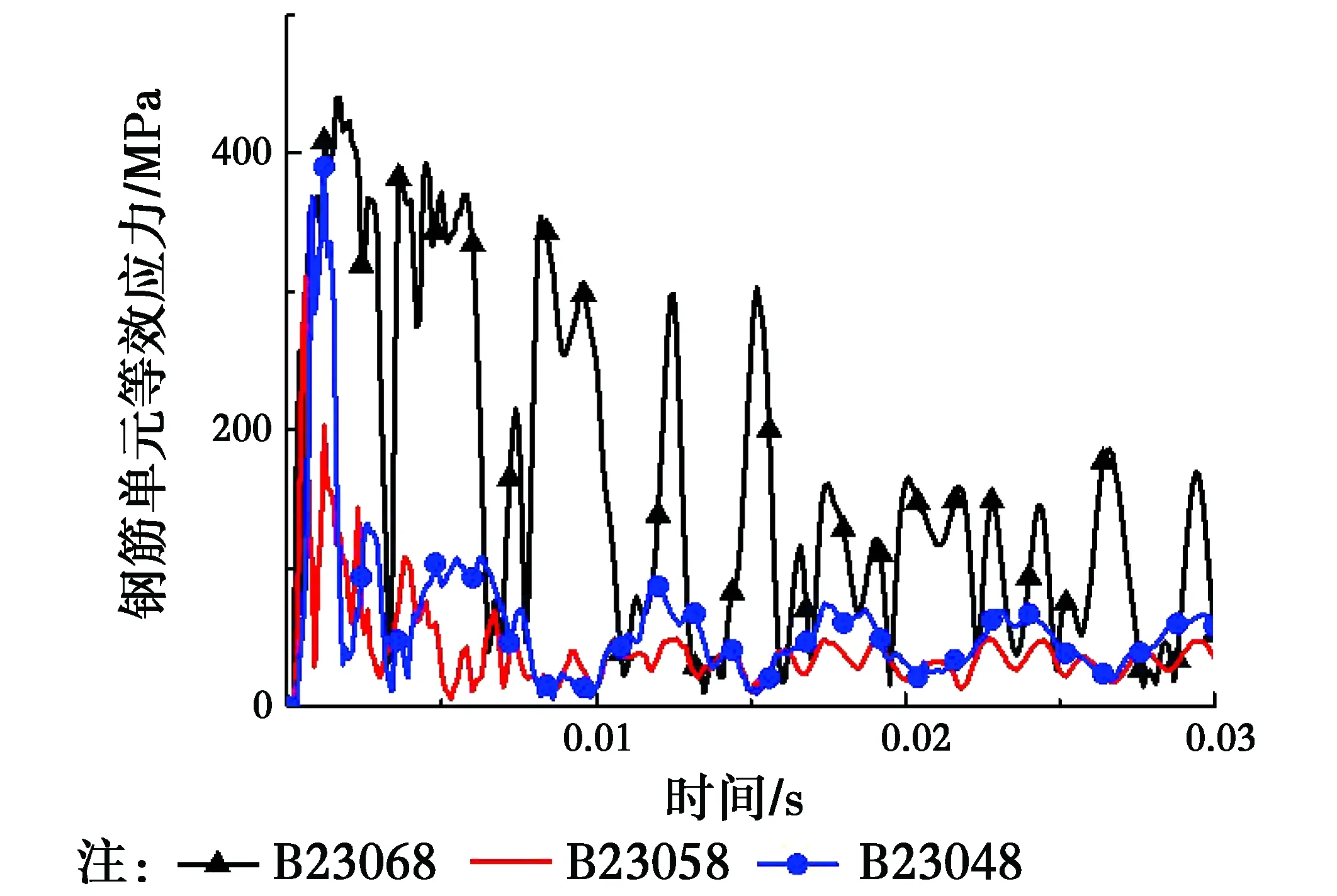
图8 钢筋等效应力时程曲线Fig.8 Effectivestress time histories of reinforced

图9给出了不同混凝土单元等效应力时程曲线。从图中可以看出，3个测点的等效应力均在开始受到爆炸荷载时急速上升，随后逐渐下降，跨中单元10476等效应力降为0，跨中混凝土被压碎失效，退出工作。支座附近单元10506、10539等效应力未超过等效屈服强度，处于弹性阶段。

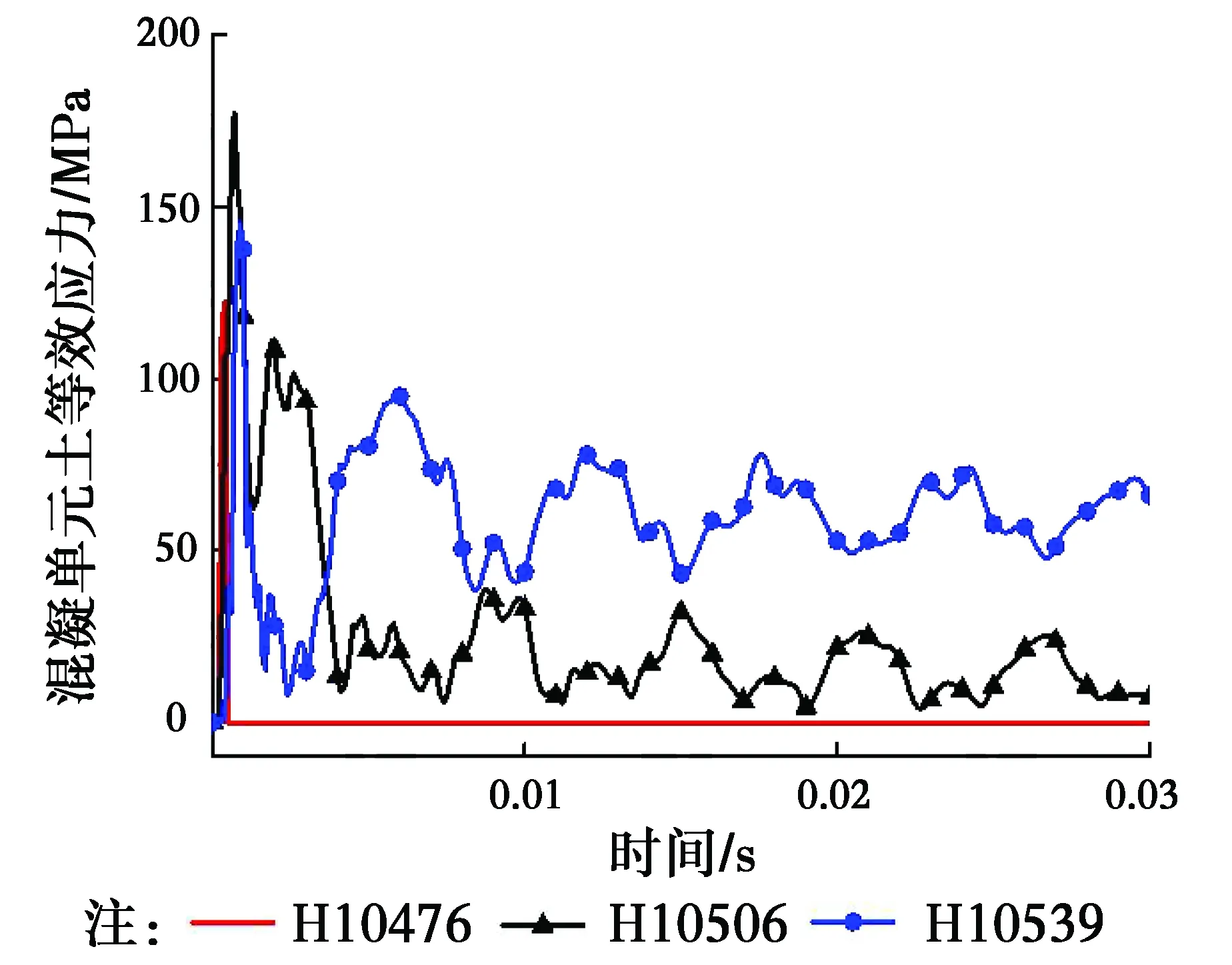
图9 混凝土单元等效应力时程曲线Fig.9 Effective stress time histories of concrete

图10给出了不同钢板节点位移时间曲线。从图中可以看出，位移在爆炸荷载作用下开始变大，然后减小趋于平稳振动，中间部分的钢板位移最大，沿支座方向的位移依次减小。

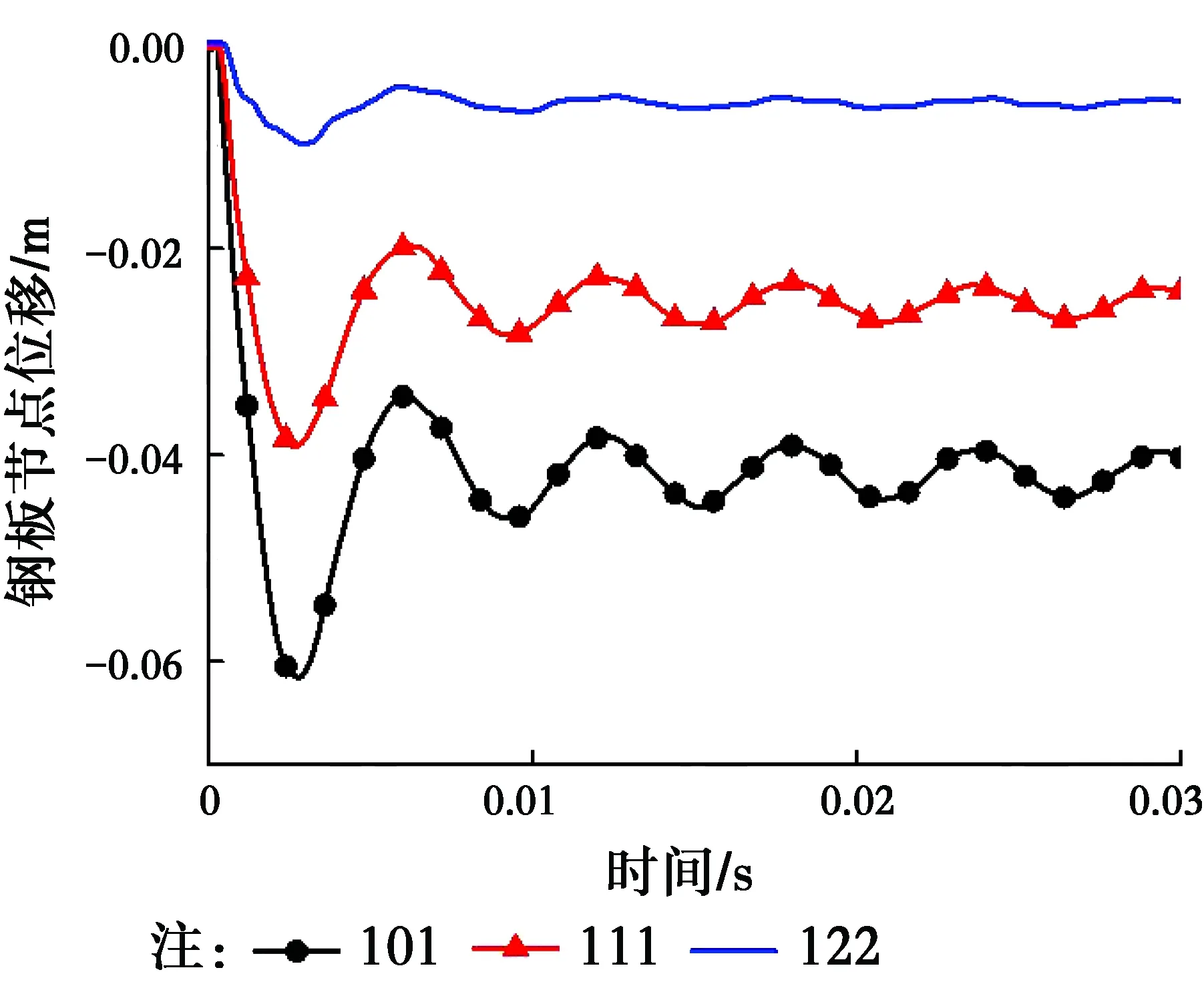
图10 钢板节点位移时程曲线Fig.10 Displacement time histories of steel plate

图11给出了不同钢板单元等效塑性应变时程曲线。在爆炸荷载作用下，爆炸荷载峰值达到最大时，等效塑性应变也达到最大，材料进入塑性状态。从图中可以看出，距离爆炸源越近，受到冲击压波力越大，因此，跨中单元117处应变最大，可达到约1.7%，单元97处应变约为0.5%，没有超过表2给出钢板的失效应变12%，表明钢板已经进入塑性阶段；77和33单元距离爆炸源较远，受到冲击波很小，产生等效塑性应变几乎为零，此处钢板单元处于弹性阶段。

图11 钢板塑性应变时程曲线Fig.11 Plastic strain time histories of steel

图12给出了钢板等效应力时程曲线。从图中可以看出，4个测点的等效应力均在开始受到冲击，压力急速上升，随后逐渐减小振动，能量也在衰减。板跨中单元117和97处于爆炸源下方，等效应力较大，在爆炸荷载作用下，考虑应变速率的影响，钢材的动力强度提高，钢板处于塑性阶段。单元77和33处由于离爆炸源较远，爆炸荷载小，等效应力较小，钢板处于弹性阶段。

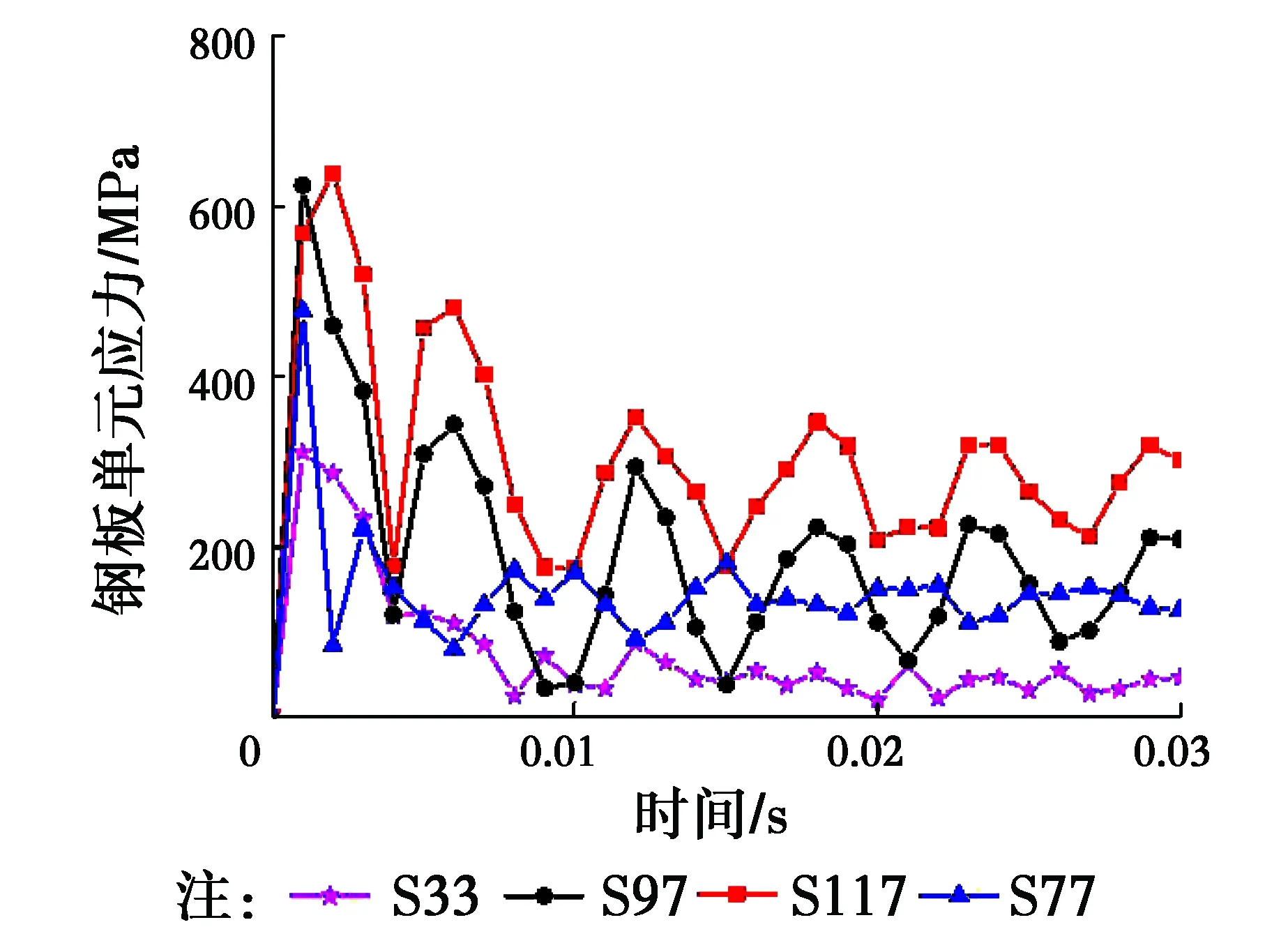
图12 钢板等效应力时程曲线Fig.12 Effective time histories of steel

3 影响组合楼板动力响应的因素分析

分析各种因素对组合楼板动力响应的影响，具体工况见表5。

在压型钢板跨中取一测点，见图13。计算出不同工况下跨中的最大位移。

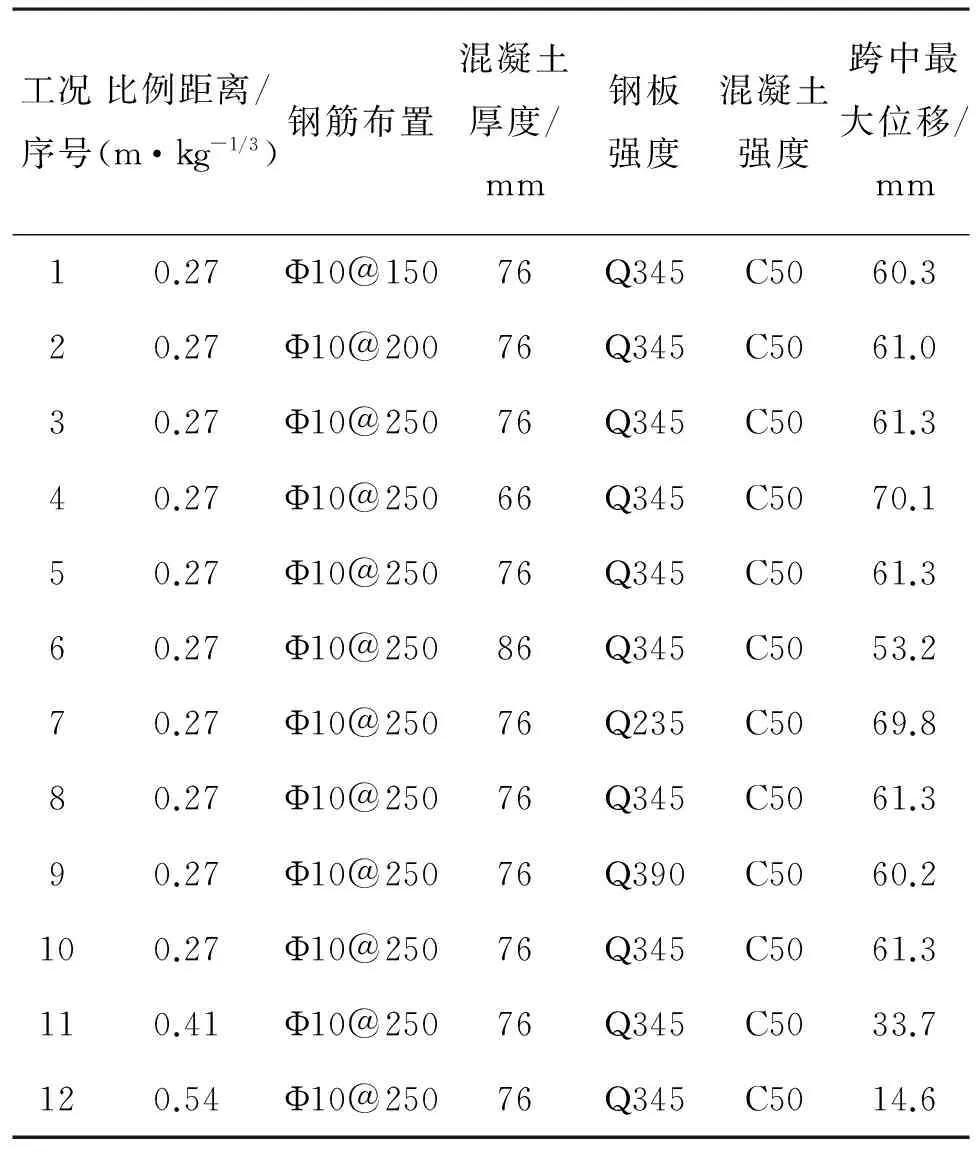
表5 不同工况对比表Table 5 Comparison of different working conditions

图13 钢板节点Fig.13 Steel plate

从表5工况1～3和图14可以看出，在其他条件不变的情况下，随着钢筋间距增加(间距150、200、250 mm)，板的最大位移稍有增加，但改变不明显。这是由于近爆作用下，混凝土几乎已被压碎，跨中部分钢筋处于弹塑性阶段。由于爆炸荷载最高可达到几十兆帕，是竖向荷载的很多倍，因此，改变间距并不能明显提高其跨中位移，在近爆荷载作用下进行组合楼板抗爆设计时，不需特别考虑减小钢筋间距，钢筋间距只须满足组合楼板正常承载力要求即可。

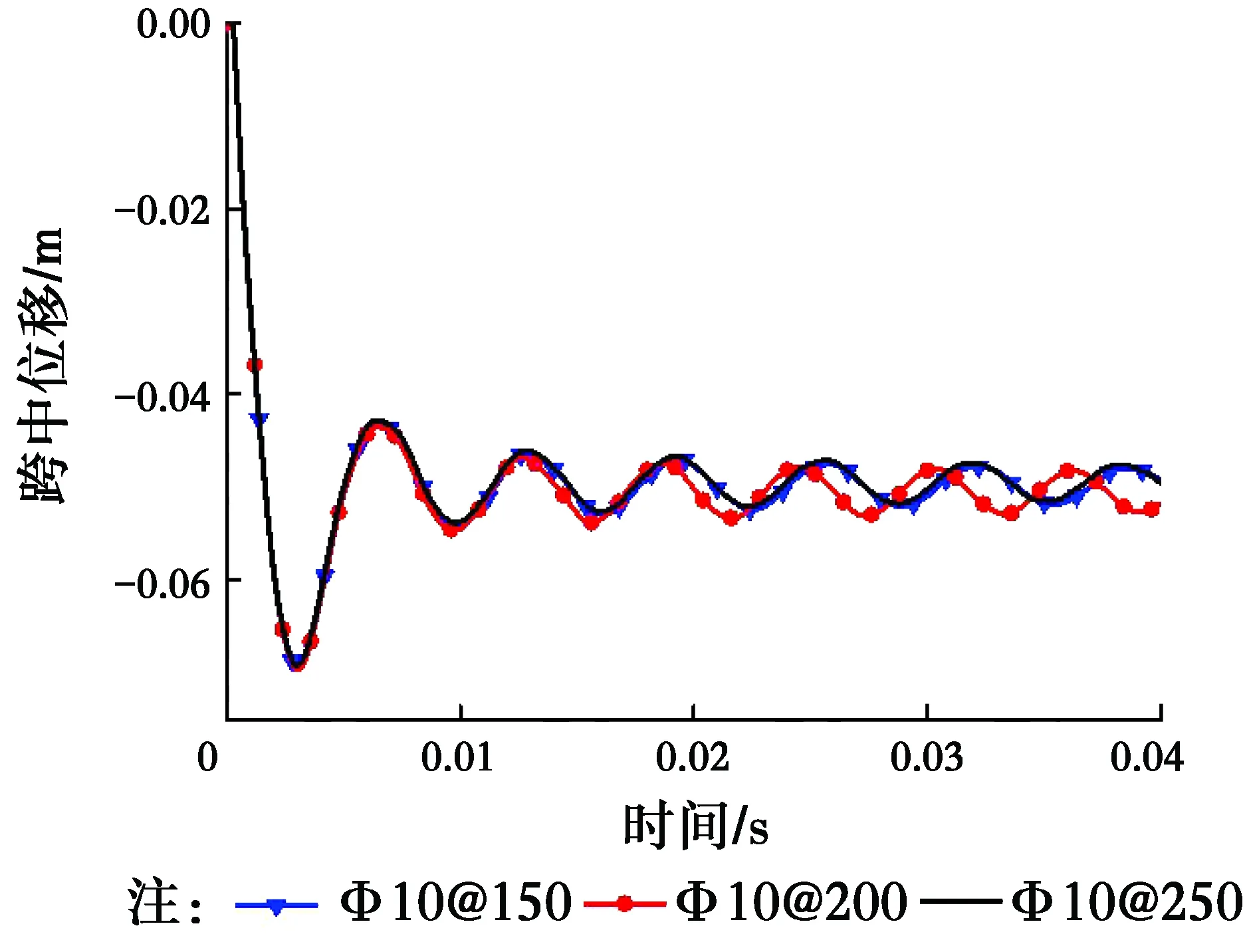
图14 不同钢筋间距跨中位移时程曲线Fig.14 Mid-span displacement time histories of different distance between

从表5工况4～6和图15可以看出，在其他条件不变的情况下，随着混凝土的厚度增加(厚度66、76、86 mm)，跨中位移变小，板厚每增加10 mm厚度(约13.2%)，跨中位移减小10 mm(约14.3%)，较为明显。这是因为增加混凝土的厚度能显著增加组合楼板的抗弯刚度，从而降低板跨中水平最大位移。同时，随着组合楼板抗弯刚度的增大，在相同的爆炸荷载作用下，混凝土尚未进入塑性的区域增多，从而有效降低了板跨中水平残余位移。

图15 不同混凝土厚度跨中位移时程曲线Fig.15 Mid-span displacement time histories of different concrete

从表5工况7～9和图16可以看出，在其他条件不变的情况下，随着钢板强度的增加(强度Q235、Q345、Q390)，跨中位移变小，钢板强度从Q345提升到Q390时，由于钢板强度提高较小，仅提高了45 MPa(约13%)，最大位移只减小了2 mm(约3.4%)，最大位移减小的程度较小；而钢板强度从Q235提升到Q345时，钢板强度提高较大，提高了120 MPa(约51%)，跨中最大位移改变较大，减小约9 mm(约12.8%)，钢板强度对位移的影响较为明显。这是因为随着钢板强度的增加，在相同的爆炸荷载作用下，组合楼板进入塑性的区域显著减少，从而有效降低板跨中点水平残余位移。

图16 不同钢板强度跨中位移时程曲线Fig.16 Mid-span displacement time histories of different steel plate

从表5工况10～12和图17可以看出，在其他条件不变的情况下，改变比例距离(Z=0.27、0.41、0.54 m/kg1/3)，当比例距离较大时，板出现高频振动，板处于弹性范围内，跨中最大位移为14 mm；当比例距离较小时，跨中位移增大，最大可达61 mm，此时大部分混凝土被压碎。比例距离从Z=0.41 m/kg1/3增大到Z=0.54 m/kg1/3时，跨中最大位移约从34 mm减小到13 mm(约减小61.7%)，残余变形位移从20 mm减小到10 mm(约减小50%)，比例距离Z=0.27 m/kg1/3增大到Z=0.41 m/kg1/3时，跨中最大位移约从61 mm减小到34 mm(约减小44.3%)，残余变形位移从45 mm减小到20 mm(约减小55.6%)。比例距离对板跨中位移的影响较为明显。

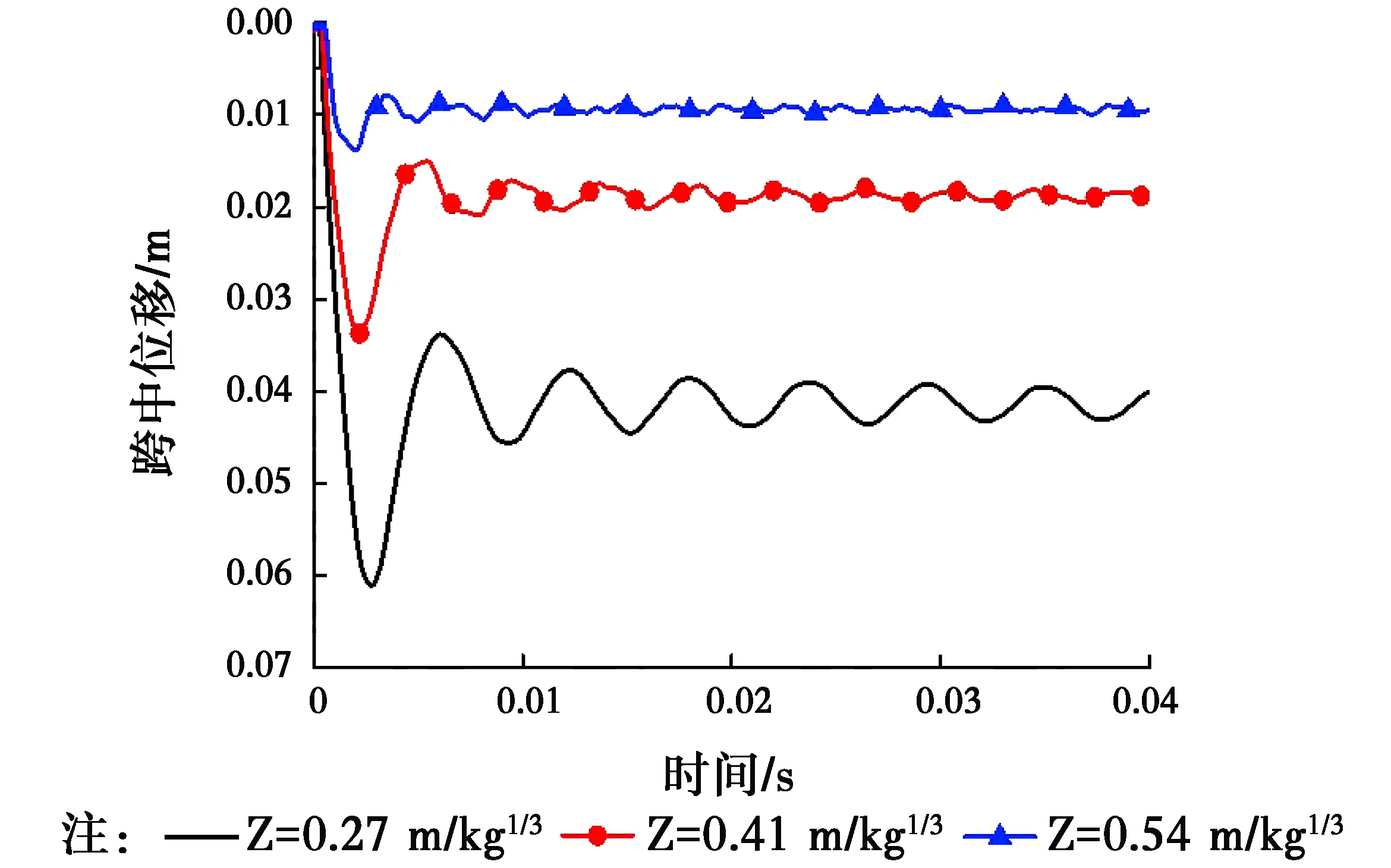
图17 不同比例距离下跨中位移时程曲线Fig.17 Mid-span displacement time histories of different scale

4 结 论

利用ANSYS/LS-DYNA有限元软件，基于流固耦合的计算方法，对爆炸源位于组合板上方近爆荷载作用下的压型钢板组合楼板单向板的动力响应及影响因素进行数值分析。得到以下结论：

1)组合楼板在爆炸荷载作用下，混凝土、钢筋和压型钢板共同作用，钢板在下层有较好的抗弯性能，塑性变形较大，但不会产生脆性破坏，在危险发生时不会产生严重破坏的现象，混凝土在上部也发挥它的抗压性能。因此，压型钢板组合楼板这种组合结构适合用于抗爆方向应用。

2)压型钢板组合楼板的混凝土厚度越大，板的跨中位移越小；钢板强度越高，板的跨中位移越小。增加组合楼板的混凝土厚度和钢板强度，均能在一定程度上提高组合楼板的延性和抗爆性能。因此，在抗爆设计时，应适当增加混凝土厚度和压型钢板强度。

3)钢筋间距的变化对压型钢板组合楼板抗爆响应影响很小，不起关键作用。进行组合楼板抗爆设计时，钢筋间距满足现行规范配筋的同时，不需特别考虑。

4)增大比例距离可以减小压型钢板组合楼板的破坏程度。比例距离越小，爆炸荷载越大，对结构破坏越严重。需要采取防爆措施，使建筑物尽可能远离爆炸源。

[1] 李国强,孙建运,王开强.爆炸冲击荷载作用下框架柱简化分析模型研究[J].振动与冲击,2007,26(1):8-11,20.

LI G Q, SUN J Y, WANG K Q. A simplified analysis model of frame column under blast impact load [J]. Vibration and Shock, 2007, 26(1): 8-11,20. (in Chinese)

[2] KARAGIOZOVA D, YU T X, LU G. Transverse blast loading of hollow beams with square cross- sections [J]. Thin-Walled Structures, 2013, 62: 169-178.

[3] THIAGARAJAN G, KADAMBI A V, ROBERT S, et al. Experimental and finite element analysis of doubly reinforced concrete slabs subjected to blast loads [J]. International Journal of Impact Engineering, 2015, 75(1): 162-173.

[4] CHEN W S, HAO H, CHEN S Y, Numerical analysis of prestressed reinforced concrete beam subjected to blast loading [J]. Materials and Design, 2015, 65(1): 662-674.

[5] 汪维,张舵,卢芳云, 等.钢筋混凝土楼板在爆炸荷载作用下破坏模式和抗爆性能分析[J].兵工学报,2010,31(Sup1):102-106.

WANG W, ZHANG D, LU F Y, et al. Reinforced concrete slab under blast loading failure mode and anti-explosion performance analysis [J]. Acta Armamentarii, 2010, 31 (Sup1): 102-106. (in Chinese)

LIU J C, RONG C, CHEN L. Dynamic responses analysis of steel-backed reinforced concrete composite beams subjected to blast loading [J]. Journal of Building Structures, 2015, 36 (Sup1): 349-354. (in Chinese)

[7] SHI Y F, STEWART M G. Damage and risk assessment for reinforced concrete wall panels: Subjected to explosive blast loading [J]. International Journal of Impact Engineering, 2015,4(85):5-19.

[8] 田力,朱聪,王浩,等.碰撞冲击荷载作用下钢筋混凝土柱的动态响应及破坏模式[J].工程力学, 2013, 30(2):150-155.

TIAN L, ZHU C, WANG H, et al. Dynamic response and failure modes of RC columns under impact [J]. Engineering Mechanics, 2013, 30(2): 150-155. (in Chinese)

[9] 崔莹,赵均海,张常光,等.复式空心钢管混凝土柱抗爆性能及损伤研究[J].振动与冲击, 2015, 34(21): 188-193.

CUI Y, ZHAO J H, ZHANG C G, et al. Explosion-resistance behavior and damage assessment of a duplex hollow CFST column subjected to blast loading [J]. Journal of Vibration and Shock, 2015, 34(21): 188-193. (in Chinese)

[10] 朱新明.钢箱梁爆炸冲击局部破坏数值模拟研究[D].长沙:国防科学技术大学,2011.

ZHU X M. Numerical simulation investigation of local failure of steel box girders under blast loading [D]. Changsha: National University of Defense Technology, 2011. (in Chinese)

[11] 丁阳,汪明,李忠献.爆炸荷载作用下钢框架结构连续倒塌分析[J].建筑结构学报,2012,33(2):78-84.

DING Y, WANG M, LI Z X. Numerical analysis on damage and collapse process of steel frame structures under blast loads [J]. Journal of Building Structures, 2012, 33(2):78-84. (in Chinese)

[12] 李世强，李鑫，吴桂英.爆炸冲击波在地铁车站内传播规律的数值模拟[J].振动与冲击,2013,32(7):175-178.

LI S Q, LI X, WU G Y. Numerical simulation of propagation law of blast wave inside a subway station [J]. Journal of Vibration and Shock, 2013, 32(7):175-178. (in Chinese)

[13] 姚宇飞,师燕超,李忠献. 爆炸荷载下钢筋混凝土框架结构连续倒塌分析方法比较[J].建筑科学与工程学报, 2015, 32(1): 64-72.

YAO Y F, SHI Y C, LI Z X. Comparison of progressive collapse analysis methods for RC frame structures under blast loads [J]. Journal of Architecture and Civil Engineering, 2015, 32(1): 64-72. (in Chinese)

[14] 高轩能,王书鹏.大空间柱壳结构爆炸动力响应的Ritz-POD数值模拟[J].土木建筑与环境工程, 2010, 32(2):64-70.

GAO X N, WANG S P. Numerical simulation for dynamic response of large-space cylindrical reticulated shell under internal explosion by Ritz-POD method [J]. Journal of Civil, Architectural & Environmental Engineering, 2010, 32(2): 64-70. (in Chinese)

[15] Livermore Software Technology Corporation. LS-DYNA keyword user’s manual [M]. Livermore，California： Livermore Software Technology Corporation, 2006.

[16] 张秀华,段忠东,张春巍.爆炸荷载作用下钢筋混凝土梁的动力响应和破坏过程分析[J].东北林业大学学报,2009,37(4):50-53.

ZHANG X H, DUAN Z D, ZHANG C W. Analysis of dynamic response and failure process of reinforced concrete beams under blast loading [J]. Journal of Northeast Forestry University, 2009, 37 (4): 50-53. (in Chinese)

[17] 李天华,赵均海,魏雪英,等.爆炸荷载下钢筋混凝土板的动力响应及参数分析[J].建筑结构,2012,42(Sup1):787-790.

LI T H, ZHAO J H, WEI X Y, et al Dynamic response and parameter analysis of reinforced concrete slab under explosive load [J]. Building Structure, 2012,42 (Sup1): 787-790. (in Chinese)

[18] 徐坚锋.CFRP钢管混凝土柱抗爆动力响应研究[D].西安:长安大学,2014.

XU J F. Analysis on the dynamic response of concrete filled CFRP-steel tube columns under explosive load [D]. Xi'an: Chang'an University, 2014. (in Chinese)

[19] 邓昭金.钢筋混凝土防爆墙性能数据分析[D].长沙:湖南大学,2012.

DENG Z J. Analysis of the performance data of reinforced concrete blast wall [D]. Changsha: Hunan University, 2012. (in Chinese)

[20] 张秀华. 燃气爆炸冲击作用下钢框架抗爆性能实验研究与数值模拟[D]. 哈尔滨: 哈尔滨工业大学, 2011

ZHANG X H. Experimental research and numerical simulation on blast resistance performance of steel frames [D]. Harbin: Harbin Institute of Technology, 2011:59-60. (in Chinese)

(编辑 胡英奎)

Provincial Key Laboratory of Open Research in Jiangsu Province(No. ZD1303)

Numerical analysis for dynamic responses and influencing factors of profiled steel-concrete composite slab under near explosion

Zhang Xiuhua1,2, Gao Shan1, Wu Jian1

(1. School of Civil Engineering, Northeast Forestry University, Harbin 150040, P. R. China;2. Jiangsu Key Laboratory of Structural Engineering, Suzhou 215011, Jiangsu, P.R.China)

Explicit dynamic finite element program ANSYS/LS-DYNA is adopted. According to the method of fluid-structure interaction, profiled steel-concrete composite slab is simulated under near explosion in different conditions. And the stress form, the dynamic responses and failure process were analysed. Numerical analysis results show that the largest displacement of composite floor slab can be significantly reduced with increasing the thickness of the concrete and improve the strength of the steel plate. The ductility and anti-explosion performance of composite floor slab can be improved. The anti-explosion performance of composite floor slab has less effect by changing reinforced spacing. The reference and basis can be provided for antiknock design of profiled steel-concrete composite slab.

blast load; composite slab; dynamic response; influencing factors; numerical analysis

10.11835/j.issn.1674-4764.2016.05.007

2016-05-16

江苏省结构工程重点实验室开放课题(ZD1303)

张秀华(1970-)，女，博士，副教授，主要从事结构工程抗爆、抗震研究，(E-mail)zhangxh2000@163.com。

TU398.9

A

1674-4764(2016)05-0050-09

Received:2016-05-16

Author brief：Zhang Xiuhua(1970-), PhD, associate professor, main research interest: blast-resistant/seismic of structure engineering, (E-mail) zhangxh2000@163.com.