复合打击下具有多次拦截时机的火力分配问题

冯超， 景小宁

空军工程大学 航空航天工程学院， 西安 710038

复合打击下具有多次拦截时机的火力分配问题

冯超， 景小宁*

空军工程大学 航空航天工程学院， 西安 710038

针对传统火力分配模型容易造成资源浪费的问题，将火力单元以组为单位，以最大化杀伤概率为目标，构建一种具有多次拦截时机的动态火力分配模型；考虑到组内火力单元复合打击的情况，使用Kuhn-Munkres算法，优先将目标分配给复合打击效果大的目标；在此基础之上，设计了一种基于遗传算法(GA)的Anytime算法，引入了元级控制，提出一种任意时刻算法停机时刻的判定方法；仿真实验验证了模型优越性以及算法的合理性，对火力分配任意时刻算法使用元级控制可以有效提高解的效用。

火力分配； 复合打击； Anytime算法； 元级控制； 多次拦截时机

火力分配，作为作战决策中的一个重要环节，是指通过合理的分配手段，将有限的武器资源分配给相应的目标，以最大化对敌方的杀伤效果[1]。模型与算法是目前研究火力分配问题中的两大热点。

模型研究的重点主要是动态火力分配模型的构建。动态火力分配相对于静态火力分配需要考虑离散时间段武器目标的分配[2]。文献[3]提出一种分阶段动态火力分配模型，将动态火力分配分为一个个阶段，利用动态规划的思想处理每个阶段目标的分配问题，虽然建立了一般意义上的动态火力分配模型，但是并没有提出合适的方法求解动态模型；文献[4]将火力分配过程视为马尔可夫模型，并利用马尔可夫决策过程进行研究，但是所建立的模型约束过多，在目标个数较大的情况下，计算量大且效率低，不具有实战价值。针对动态火力分配问题，本文将火力单元分组，以组为单位进行分配，考虑到目标到达不同火力单元具有时间差的特点，建立了一种考虑多次拦截时机的动态火力分配模型，具有一定的实战价值。一般情况下，关于火力分配的文献[5-10]大多认为火力打击行动之间是相互独立的，并没有考虑到复合打击的问题，而本文在同组火力单位中将考虑复合打击的情况。

对算法的研究，动态火力分配问题是一个多参数、多约束的NP-完全问题[11]，具有复杂度高、计算量大的特点，使用单纯型法、分解算法以及隐枚举法等传统求解模型不能满足实际需求；近年也涌现出了许多智能算法，例如：遗传算法(Genetic Algorithm, GA)[12]、蚁群算法[13]、粒子群算法[14]、多目标进化算法[15]等；文献[16]便提出使用Anytime算法求解动态火力分配模型。本文根据建立的具有多次拦截时机火力分配模型，设计一种多次拦截时刻的改进遗传算法(Modified Genetic Algorithm at Multiple Interception Opportunities, MIO-MGA)。最后，对MIO-MGA算法引入元级控制(Meta-level Control)，并且设计了一种算法停机时刻的判定方法。

1 火力分配模型

防空作战火力分配的主要原则是：优先打击杀伤概率大的目标，尽量减少己方武器消耗，使得全局达到最优分配。在实际防空作战中，敌方目标进入我方火力覆盖区域是有时间差的。考虑这一特点，本文将我方作战的火力单元以组为单位进行划分，使用不同火力单元组对同一目标进行多次打击。不仅可以充分提高我方对敌机整体的打击效果，并且能够减少我方武器消耗，还为每个火力单元赢得了宝贵的准备时间，使整体达到了最优的分配；在火力单元组内，模型考虑了不同武器攻击时复合打击的问题，求解出火力单元组内复合打击条件下的最大毁伤效果。

1.1 模型的建立

根据实际防空作战中，目标到达不同火力单元攻击范围有时间差的特点，可以使用不同火力单元对同一目标进行多次打击。假如通过某种约束，使打击相同目标的火力单元在不同时刻进行打击，则火力单元具有多次拦截时机。如图1所示，目标从右向左通过火力单元A与B。在t1时刻，火力单元A可以对目标进行攻击。如果没有击落目标，那么在t2时刻目标进入火力单元B的攻击范围，火力单元B也可以攻击目标。如果时间间隔足够长，火力单元A完成装弹，那么在时刻t2，火力单元A还可以对目标进行第二次打击。如果设置合适的时间间隔，可以使火力单元多次打击目标，不仅节约弹药，更为火力单元赢得宝贵的装填弹药的时间。

图1 火力单元多次拦截时机示意图 Fig.1 Schematic diagram of fire unit at multiple interception opportunities

图2 火力单元组示意图Fig.2 Schematic diagram of fire unit group

(1)

若目标Nj的价值为vj，则本文建立的考虑多次拦截时机的火力分配模型为

(2)

约束如下：

1) 决策变量为0-1整数，即xij={0,1}。

1.2 毁伤效果计算

本文考虑火力单元组内复合打击的情况。在实际作战中，复合打击被广泛使用，对同一目标同时使用两种或两种以上武器进行打击，造成的杀伤效果远远高于分别使用武器进行攻击。例如，在打击坚固防御工事下的有生力量时，可以首先使用穿甲弹药对工事进行破坏，在打开一个缺口后，投放航爆弹钻入工事进行内部打击，造成预定的杀伤效果。这两种武器就存在复合打击的情况。为简化模型，本文将同一火力单元组内不同的火力单元各自视作一种武器，只分析两种不同火力单元之间复合打击的情况，对多种火力单元的复合打击不做分析。

uj(ailj)=-lb(1-pilj)

(3)

uj(ailj,aikj)=uj(ailj)+uj(aikj)

(4)

uj(ailj,aikj)>uj(ailj)+uj(aikj)

(5)

这里仅考虑复合打击效果大于各自独立打击的情况，即复合打击正相关的情况。记复合打击效率为γ(ailj,aikj)，则有

uj(ailj,aikj)=(1+γ(ailj,aikj))(uj(ailj)+

uj(aikj))

(6)

1) 若火力单元组内火力单元个数为偶数

图3 火力单元组复合打击拓扑结构 Fig.3 Topology description of fire unit group in composite strikes

假如Λ⊂E(G)，∀eλ1,eλ2∈Λ，且eλ1与eλ2都没有相同端点(λ1≠λ2)，则Λ为图G中的一个对集，而Λ中任意一边的两个端点称为在对集Λ里相配。假如图G中每一个节点都被Λ许配，则Λ被称为完美对集。霍尔(Hall)定律表明，二分图G中，若X与Y是图G中节点集合的划分，则G中存在把X中节点皆许配的对集的充要条件是，∀S⊂X，|N(S)|≥|S|，N(S)为S中节点的邻集。进一步可知，假如G为d(d>0)次正则二分图，则G一定存在完美对集。

根据假设，加权无向图G=(M(G),E(G))描述火力单元在复合打击条件下的拓扑结构满足存在完美对集条件，可以使用Kuhn-Munkres算法求解完美对集，进而求解全局打击效果最大的打击方案。为方便计算，需要引入可行节点标号与相等子图的概念。

定义1(可行顶点标号)：假如存在映射φ∶M(G)→R，使得∀x∈X，y∈Y，φ(x)+φ(y)≥uj(x,y)成立，则称φ为二分图G的可行顶点标号。令

Eφ={x,y|x,y∈E(G),φ(x)+φ(y)≥

uj(x,y)}

(7)

称以Eφ为边集的G的生成子图为相等子图，以Gφ表示。

这里给出Kuhn-Munkres算法的具体计算过程。

步骤1选取初始可行顶点标号φ，得到Gφ，确定对集Λ。

步骤2假如X中的顶点被Λ全部许配，停机并输出结果，则图G中权最大的完美对集即为Λ；否则，任取Gφ中一未被Λ许配的顶点q，令S={q}，B=∅。

步骤3假如NGφ(S)⊃B(NGφ(S)为Gφ中S的相邻节点集合)，转步骤4；假如NGφ(S)=B，令

(8)

(9)

并转步骤2。

2) 若火力单元组内火力单元个数为奇数

本节给出求解火力单元组内复合打击效果的Kuhn-Munkres算法步骤，需要讨论算法的时间复杂度。对于Kuhn-Munkres算法步骤，每个顶点都需要作一次可增广轨，所以有n个循环。在每个循环内部，在无法得到一条可增广轨时(该情况下的时间复杂度为O(n))，需要新加入一个点κ，然后重新寻找可增广轨。一次最少加入1个点，所以最多加入n次。每次重新寻找可增广轨的时间复杂度为O(n)，更新顶点标号需要扫描每一条边的时间复杂度为O(n2)，所以迭加起来后的复杂度为O(n)*O(n)*O(n2)。综合考虑，标准Kuhn-Munkres算法总时间复杂度为O(n4)。

若对标准Kuhn-Munkres算法进行工程改进，可以在每个Y顶点上定义一个函数slack(·)。当计算增广轨时，首先令函数slack(·)为一极大值；在每次寻找增广轨的过程中，时刻检查边e(i,j)，假如相等子图中没有此条边，则令slack(j)等于原值与X(i)+Y(j)-u(i,j)中的较小的一个数值。通过设置函数slack(·)，可以降低修改顶标的复杂度。将标准Kuhn-Munkres算法的时间复杂度降低到O(n3)。

虽然Kuhn-Munkres算法的时间复杂度较高，但是在实际作战中，己方的火力单元个数不会很大，并且考虑到式(2)中的约束条件式(3)，使得每个火力单元组内的火力单元个数也不会很大；一般火力单元组内的火力单元个数小于6，而这个复杂度是可以接受的。

2 带元级控制的Anytime算法

根据本文的假设，进入火力单元防区目标的进入方向是确定的，但是并没有确定单批目标Nj进入防区的时间。合适的火力分配方案需要在目标Nj进入火力单元防区前制定出来，即每个目标均有一个截止时间，所用算法应使当前目标分配结果运行的时间少于当前目标的截止时间，这要求算法能够实时地给出计算结果。一般文献[16,18]求解此类问题时，均使用Anytime算法。在Anytime算法中，解的质量与时间成正相关，计算时间越长，解的质量越好，且算法可以随时停止并输出结果，这个特性对于求解动态火力模型极其有用。文献[18]指出，虽然Anytime算法可以确保解的质量随时间增加而增加，但是解的效用不一定会随时间增加而增加，这时就需要一种元级控制过程来对算法进行控制，以便确定算法合适的停机时刻。

2.1 Anytime算法描述

文献[18]提出一类基于遗传算法的Anytime算法，命名为MGA(Modified GA)算法。使用该算法求解带截止时间约束的火力分配问题，可在执行过程中随时处理新的目标。

若初始状态为：m个火力单元Mi对n个目标Nj进行拦截，并为每个目标设置一个截止时刻。

具体算法步骤为：

步骤1初始化n个目标的截止时刻数组，并按照时间先后顺序排序。

步骤2设定MIO-MGA算法中基本遗传算法的遗传与变异算子，设定最优个数数目以及相应算法参数。

步骤4构建染色体长度为火力单元组个数g的染色体种群，并计算每个火力单元组中最大的复合打击效果。其中，与标准遗传算法类似，染色体中每个基因位即为目标序号，染色体的适应度函数使用式(2)计算。

步骤5使用式(2)中的约束条件式(3)对染色体种群进行筛选。

步骤6对每一代的种群进行遗传操作，将非劣解直接保留到下一代，保证解质量非减。若算法满足Anytime算法元级控制停止条件时，即可停机并输出结果，否则转步骤7。

步骤7使用遗传操作得到的最优解中的染色体中当前目标所对应的基因位即为需要分配的火力单元组。

步骤8若目标被分配后，更新截止时刻数组，并重复步骤2～步骤7，直到所有目标被分配完毕。

其中，筛选方法如下：

2.2 元级控制的改进

Anytime算法尽管可以保证解的质量会随时间的增加而增加，但是不能保证解的效用也随时间的增加而增加。如果对Anytime算法增加元级控制方法，则可以在每个目标截止时刻之前即时输出效用最大的解，将算法的整体效用进行优化，以提高算法的性能。

文献[16]给出了Anytime算法的一种元级控制方法。但是对于Anytime停机时刻的判断方法并不明确，且存在算法在目标截止时刻之前尚不能判断算法停机时刻的情况。本节对文献[16]中的元级控制方法进行改进，提出一种Anytime算法停机时刻新的判定方法。

文献[19-20]通过定义一个与时间相关的效用函数来对Anytime算法进行元级控制，用来表示一段时间内解的效用数值。如果某时刻的效用函数达到最大值，则在当前时刻由Anytime算法计算出的目标分配方案就是最合适的。文献[18]中所给出的效用函数由3部分组成：算法运行时解的质量与实际最优解质量的比值、未分配目标数量对于解效用的影响以及目标分配时间对于效用的影响。这里直接给出文献[18]中3个指标的计算公式：

1) 解质量与实际最优解质量比值对于解效用的影响。

2) 未分配目标数量对于解效用的影响。

3) 目标分配时间对于解效用的影响。

对于每个目标而言，处理目标使用时间的长短也会影响解的效用，该影响可使用公式Uc=-(T*-t)-2计算，T*为最近的一个截止期。

综合算法运行时解的质量与实际最优解质量的比值、未分配目标数量与目标分配时间对于效用的影响，可以得到关于时间的效用函数公式为

U(t)=ω1Uμ(t)+ω2Us(t)+ω3Uc(t)

(10)

式中：ω1、ω2和ω3分别为算法运行时解的质量与实际最优解质量的比值、未分配目标数量与目标分配时间对于效用影响的权重，依据具体模型设定。

文献[18]虽然给出了效用函数的计算公式，但是并没有指出何时效用函数可以达到最大值，以及如何判断算法的停机时刻。要想求得效用函数的最大值，必须将目标截止时刻之前所有时刻的效用函数值全部求解出来，但是在截止时刻才得到效用函数值的最大值已经失去了实际意义。为此，本文给出一种Anytime算法在进行元级控制时算法停机时刻的判定方法。

U(k)=ω1Uμ(k)+ω2Us(k)+ω3Uc(k)

(11)

3 仿真与分析

仿真实验初始设定如下：假设我方有火力单元20个，敌方目标个数为10，每个目标到第一个火力单元的截止时间服从均匀分布，区间范围为[5,30] s；目标到达每个火力单位之间的时间服从均匀分布，区间范围为[5,10] s；每个火力单元对目标的毁伤概率服从均匀分布，区间范围为[0.2,0.8]；火力单元之间的复合打击效率除对角线元素为0外，其余元素在区间[0,0.5]之间服从均匀分布；目标价值在区间[10,50]之间服从均匀分布；如果一个旧目标被分配完成，一个新目标将会产生，直至所有目标都分配完成，新目标的初始条件同上；式(2)的约束条件式(3)中的常数项C=2，将火力单元分配给10个旧目标后实验结束；而采用的遗传算法中种群的染色体个数为100，交叉和变异的概率为0.8和0.2；实验引入元级控制，其中影响权重ω1，ω2和ω3分别设定为2，2，0.2；进行以下实验：① 在不进行元级控制条件下，分别使用MGA算法和本文给出的MIO-MGA算法求解火力分配问题，此时，Anytime算法的截止时间即为当前目标的截止时间；在进行元级控制的条件下(元级控制停止准则使用本文给出的停机准则)，分别使用MGA算法和MIO-MGA算法求解火力分配问题；② 分两种情况使用本文给出的MIO-MGA算法求解火力分配问题，一种为不进行元级控制，即：MIO-MGA算法的停机时间为当前目标的截止时间；另一种为使用本文给出的元级控制方法求解；通过求解目标适应度和效用值两个实验对比元级控制的优越性；③ 讨论在目标数量较大情况下MGA算法和MIO-MGA算法的性能，即分别使用MGA算法和MIO-MGA算法在目标数量较大情况下求解本文给出的火力分配模型。

3.1 Anytime算法性能对比

1) 在不进行元级控制的条件下，测试MGA算法与本文提出的MIO-MGA算法求解火力分配问题的性能。图4给出了10个旧目标被处理完成后，每个目标被火力单元打击造成的毁伤效果，即算法中每个目标的适应度，其中目标序号按照先后被处理的顺序排列。

从图4中可以看出，每个目标通过MIO-MGA算法计算出的适应度明显比通过MGA算法得到的适应度高，平均高出12.5%。这是因为，MIO-MGA算法相比于MGA算法，通过火力单元分组操作、筛选染色体操作降低了计算的复杂度，使得算法的计算时间相对缩短；而MIO-MGA算法的适应度随时间变化是非负的，在不进行元级控制的情况下，对于同一个目标，使用MIO-MGA算法可以多次进行计算，所以得到的解的质量相对较好。

图4 两种算法求解的毁伤效果对比Fig.4 Contrast for damage effect of two algorithms

2) 在使用本文给出的元级控制方法的条件下，测试MGA算法与本文MIO-MGA算法求解火力分配问题的性能。图5给出了10个旧目标被处理完成后，算法处理每个目标所用的时间，即算法迭代的次数，其中目标序号按照先后被处理的顺序排列。

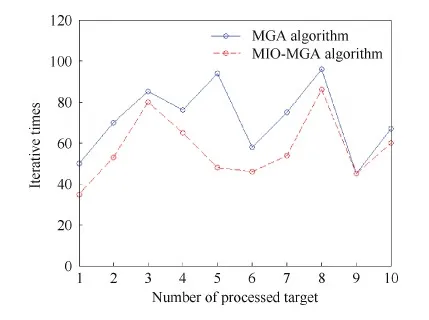
图5 不同目标的迭代次数Fig.5 Iterative times of different targets

图5验证了使用MIO-MGA算法可以有效降低计算复杂度，减少了目标计算的时间。通过引入元级控制，MIO-MGA算法的运行时间明显减少，而解的效用明显增加。算法迭代次数平均减少了17.5%。

3.2 元级控制效果对比

分别测试在有元级控制和没有元级控制条件下，使用MIO-MGA算法求解本文给出的火力分配模型。

图6给出了10个旧目标被处理完成后，每个目标被火力单元打击造成的毁伤效果。由图6可以看出，在MIO-MGA算法运行过程中，元级控制的引入虽然使解的质量差于不使用元级控制的MIO-MGA算法(解质量平均下降了23.4%)，但是减少了算法运行的时间，使得解的效用得到了综合提升。

图7给出了10个旧目标被处理完成后，每个目标当时的解的效用值。

图7说明虽然引入元级控制会降低解的质量，但是通过加入元级控制，减少了运行时间，提高了解得效用值。如图7所示，使用元级控制后的算法解的效用值提高了29.8%。这一点在实战中相当重要，以往的火力分配模型并没有考虑到火力单元装填弹药修整的时间，引入元级控制，可以节约出大量时间，使得算法更具有实际意义。

图6 有无元级控制下的毁伤效果对比Fig.6 Contrast for damage effect with and without meta-level control

图7 有无元级控制下不同目标的效用值Fig.7 Utility of different targets with and without meta-level control

3.3 目标数量较大情况下的算法性能对比

分别测试MGA算法和MIO-MGA算法在目标数量较大情况下算法求解问题的性能，即测试算法实际运行所用的时间。

这里为消除动态目标飞到火力单元上空存在时间差对算法实际运行时间带来的影响，所以在这个实验中引入元级控制，计算带元级控制的两种算法在目标数量较大条件下实际运行的时间。测试平台使用Intel Core i5处理器，运行内存为4 GB，基于MATLAB 2010编程实现。图8分别给出了两种算法处理目标时所运行的总时间。其中，两种算法的总时间是指算法用于求解火力分配模型所用的时间之和，不包括等待目标的时间。

图8 两种算法运行的总时间Fig.8 Total time of two algorithms

从图8中可以看出，在目标数量较大的情况下，MIO-MGA算法比MGA算法所用的总时间要少。在处理100个目标的时候，MGA算法处理一个目标平均的时间只有MIO-MGA算法一半。并且随目标数量的增加，这种差距会逐渐增大，说明了在目标数量较大的情况下，MIO-MGA算法性能远远好于MGA算法。

4 结 论

1) 本文建立了一种考虑多次拦截时机的动态火力分配模型，通过分批次打击敌方目标，为每个火力单元赢得了宝贵的准备时间，具有一定的实战价值，也为动态火力分配的研究提供了一种新的解决思路。

2) 传统上动态火力分配算法在目标数量较大情况下，所耗时间极长，不具备实际意义。而本文改进算法大大减少了算法运行时间，对于作战自主控制有一定的参考价值。

3) 本文在计算火力单元复合毁伤效果时，仅仅考虑两种不同火力单元复合打击的情况，没有分析多个火力单元直接的复合打击效果。而实际作战中存在多个火力单元复合打击的情况，所以在未来的研究中，可以考虑计算多个火力单元的毁伤效果。

[1] MEHMET A S, KEMAL L. Approximation the optimal mapping for weapon-target assignment by fuzzy reasoning[J]. Information Science, 2014, 255(1): 30-44.

[2] BAYRAK A E, PLOAT F. Employment of an evolutionary heuristic to solve the target allocation problem efficiently[J]. Information Sciences, 2013, 222(3): 675-695.

[3] HOSEIN P, ATHANS M. Preferential defense strategies, Part 2: The dynamic case: LIDS-P-2003[R]. Massachusetts: Massachusetts Institute of Technology, 1990.

[4] 蔡怀平， 刘靖旭， 陈英武. 动态武器目标分配问题的马尔可夫性[J]. 国防科技大学学报， 2006， 28(3): 124-126.

CAI H P, LIU J X, CHEN Y W. On the Markov characteristic of dynamic weapon target assignment problem[J]. Journal of National University of Defense Technology, 2006, 28(3): 124-126 (in Chinese).

[5] 陈黎， 王中许， 武兆斌， 等. 一种基于先期毁伤准则的防空火力优化分配[J]. 航空学报， 2014， 35(9)： 2574-2582.

CHEN L, WANG Z X, WU Z B, et al. A kind of antiaircraft weapon-target optimal assignment under earlier damage principle[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(9): 2574-2582 (in Chinese).

[6] 王少蕾， 陈维义， 顾雪峰. 自适应差分进化算法求解多平台多武器-目标分配问题[J]. 系统工程与电子技术， 2013， 35(10)： 2116-2118.

WANG S L, CHEN W Y, GU X F. Solving weapon-target assignment problems based on self-adaptive differential evolution algorithm[J]. Systems Engineering and Electronics, 2013, 35(10): 2116-2118 (in Chinese).

[7] 顾骥， 李相民， 刘立佳， 等. 基于Memetic算法的超视距协同空战火力分配[J]. 北京航空航天大学学报， 2014， 40(10): 1424-1426.

GU J, LI X M, LIU L J, et al. Weapon-target assignment based on Memetic optimization algorithm in beyond-visual-range cooperative air combat[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(10): 1424-1426 (in Chinese).

[8] 贺小亮， 毕义明. 基于模拟退火遗传算法的编队对地攻击火力分配建模与优化[J]. 系统工程与电子技术， 2014， 36(5): 900-903.

HE X L, BI Y M. Modeling and optimization of formation air-to-ground attack fire distribution based on simulated annealing genetic algorithm[J]. Systems Engineering and Electronics, 2014, 36(5): 900-903 (in Chinese).

[9] 张姣， 王中许， 陈黎， 等. 具有多次拦截时机的防空火力分配建模及其优化方法研究[J]. 兵工学报， 2014， 35(10): 1644-1647.

ZHANG J, WANG Z X, CHEN L, et al. Modeling and optimization on antiaircraft weapon-target assignment at multiple interception opportunity[J]. Acta Armamentarii, 2014, 35(10): 1644-1647 (in Chinese).

[10] 张毅， 姜青山， 陈国生. 具有条件风险值的动态火力分配方法[J]. 系统工程与电子技术， 2012， 34(2)： 313-316.

ZHANG Y, JIANG Q S, CHEN G S. Dynamic weapon-target assignment with conditional value-at-risk[J]. Systems Engineering and Electronics, 2012, 34(2): 313-316 (in Chinese).

[11] LIOYD S P, WITSENHAUSEN H S. Weapon allocation is NP-complete[C]//Proceedings of the IEEE Summer Simulation Conference. Piscataway, NJ: IEEE Press, 1986: 1054-1058.

[12] LEE Z J, SU S F, LEE C Y. Efficiently solving general weapon-target assignment problem by genetic algorithm with greedy eugenics[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2003, 33(1): 113-121.

[13] 罗德林， 段海滨， 吴顺详， 等. 基于启发式蚁群算法的协同多目标攻击空战决策研究[J]. 航空学报， 2006， 27(6): 1166-1170.

LUO D L, DUAN H B, WU S X, et al. Research on air combat decision-making for cooperative multiple target attack using heuristic ant colony algorithm[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(6): 1166-1170 (in Chinese).

[14] 李俨， 董玉娜. 基于SA-DPSO混合优化算法的协同空战火力分配[J]. 航空学报， 2010， 31(3)： 626-631.

LI Y, DONG Y N. Weapon-target assignment based on simulated annealing and discrete particle swarm optimization in cooperative air combat[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(3): 626-631 (in Chinese).

[15] 张滢， 杨任农， 左家亮. 基于分解进化多目标优化算法的火力分配问题[J]. 系统工程与电子技术， 2014， 36(12)： 2436-2438.

ZHANG Y, YANG R N, ZUO J L. Weapon-target assignment based on decomposition-based evolutionary multi-objective optimization algorithms[J]. Systems Engineering and Electronics, 2014, 36(12): 2436-2438 (in Chinese).

[16] 吴玲， 卢发兴， 贾培发. 动态武器目标分配问题中改进遗传算法的元级控制[J]. 清华大学学报(自然科学版)， 2008， 48(S2)： 1763-1764.

WU L, LU F X, JIA P F. Meta-level control of the anytime algorithm for the dynamic weapon-target allocation problem[J]. Journal of Tsinghua University (Science & Technology), 2008, 48(S2): 1763-1764 (in Chinese).

[17] 余晓晗, 徐泽水, 刘守生, 等. 复合打击下的火力分配方案评估[J]. 系统工程与电子技术, 2014, 36(1): 84-86.

YU X H, XU Z S, LIU S S, et al. Evaluations of fire assignment alternatives in the situation of composite strikes[J]. Systems Engineering and Electronics, 2014, 36(1): 84-86 (in Chinese).

[18] WU L, WANG H Y, LU F X, et al. An anytime algorithm based on modified GA for dynamic weapon-target allocation problem[C]//Proceedings of IEEE World Congress on Computational Intelligence. Piscataway, NJ: IEEE Press, 2008.

[19] ZILBERSTEIN S. Meta-level control of approximate reasoning: A decision theoretic approach[J]. International Symposium on Methodologies for Intelligent System, 1994, 869: 114-123.

[20] HANSEN E A, ZILBERSTEIN S. Monitoring and control of anytime algorithms: A dynamic programming approach[J]. Artificial Intelligence, 2001, 126(1-2): 139-157.

冯超男， 硕士研究生。主要研究方向： 航空兵任务规划与训练效能评估。

Tel.: 029-84787056

E-mail: fengchaoacmi@outlook.com

景小宁女， 博士， 副教授， 硕士生导师。主要研究方向： 航空兵任务规划。

Tel.: 029-84787056

E-mail: jxning157@sina.com

*Correspondingauthor.Tel.：029-84787056E-mail:jxning157@sina.com

Weapontargetassignmentatmultipleinterceptionopportunitiesincompositestrikes

FENGChao,JINGXiaoning*

CollegeofAeronauticsandAstronautics,AirForceEngineeringUniversity,Xi’an710038,China

Adynamicweapontargetassignmentmodelatmultipleinterceptionopportunitiesisconstructedsincethetraditionalweapontargetassignmentmodeliseasytocausewasteofresources.Thefireunitsaregroupedtooptimizethekillprobability.Consideringthecompositestrikesoffireunitsingroups,targetwithbetterstrikeperformanceispreferentiallyassignedbyKuhn-Munkresalgorithm.Ananytimealgorithmbasedongeneticalgorithm(GA)isthendesigned,andmeta-levelcontrolisintroduced.Astoptimingdeterminationmethodofanytimealgorithmisproposed.Simulationexperimentsverifytherationalityofthemodelandalgorithm,andshowthatthealgorithmcanincreaseutilitysignificantly.

weapontargetassignment;compositestrike;anytimealgorithm;meta-levelcontrol;multipleinterceptionopportunity

2015-11-16；Revised2015-12-21；Accepted2016-03-15；Publishedonline2016-03-291455

URL：www.cnki.net/kcms/detail/11.1929.V.20160329.1455.002.html

s：NationalScienceFundforDistinguishedYoungScholars(71501184);AeronauticalScienceFoundationofChina(20155196022)

2015-11-16；退修日期2015-12-21；录用日期2016-03-15； < class="emphasis_bold">网络出版时间

时间：2016-03-291455

www.cnki.net/kcms/detail/11.1929.V.20160329.1455.002.html

国家杰出青年科学基金 (71501184)； 航空科学基金 (20155196022)

*

.Tel.：029-84787056E-mailjxning157@sina.com

冯超， 景小宁. 复合打击下具有多次拦截时机的火力分配问题J. 航空学报，2016，37(11):3444-3454.FENGC,JINGXN.WeapontargetassignmentatmultipleinterceptionopportunitiesincompositestrikesJ.ActaAeronauticaetAstronauticaSinica,2016,37(11):3444-3454.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0082

V271.4

A

1000-6893(2016)11-3444-11