一种无人机定距盘旋跟踪制导律及稳定性证明

张民， 田鹏飞， 陈欣

南京航空航天大学 自动化学院， 南京 211106

一种无人机定距盘旋跟踪制导律及稳定性证明

张民*， 田鹏飞， 陈欣

南京航空航天大学 自动化学院， 南京 211106

对地面目标的定距盘旋跟踪问题是无人机(UAVs)在任务应用阶段需要面临的重要问题之一，如何在传感器信息受限的情况下完成跟踪任务是目前的研究热点。首先针对地面固定目标设计了一种仅依赖测距传感器的制导律，不再需要传统的视线角信号以及目标和无人机自身的定位信息；其次，设计了李雅普诺夫函数对该制导律的稳定性进行了严格数学证明；最后，将该制导律推广到对地面匀速和变速移动目标的跟踪制导。相比于现有制导律，所提出的制导律结构更为简洁，仅有一个设计参数，并且制导策略更为合理。仿真结果表明所提出的制导律能够实现无人机对地面固定和移动目标的稳定跟踪。

无人机(UAV); 盘旋; 地面目标; 制导律; 稳定性

无人机定距跟踪是指无人机在跟踪地面目标时总是与目标保持预先指定的某个固定距离的一种跟踪方法，对于固定翼无人机来说则是指定距盘旋跟踪的方法。定距跟踪在军用无人机对地面敏感目标的侦查监视、民用无人机搜索救护等领域均有广泛的应用[1-2]。传统的制导律设计通常需要较多无人机与地面目标的相对关系信息，如无人机位置、速度、航向、相对视线角、视线角速率以及目标位置等传感器信息[3-5]。目前无人机通常配备北斗或GPS接收机用于定位，较大型的无人机还配有惯导、大气数据系统、红外/可见光观瞄设备、激光测距仪等传感器，可为无人机制导系统提供多种信息源。然而，随着无人机使用环境的严酷，如外源定位信息失效、观瞄设备受干扰、惯导不支持长时间工作、传感器故障等条件下如何利用尽可能少的信息来完成无人机对地面目标的跟踪制导是当前定距跟踪所面临的主要问题。

在传感器信息受限的无人机制导问题中，无人机速度(地速或在制导精度要求不高时用空速代替)是必不可少的信息，在此基础上最常见的组合是采用相对距离/视线角的制导策略[6-7]，从实际设计过程来看这是一种难度相对较低的组合策略，需要测距和视觉两种传感器；另一种是基于视线角/视线角速率的制导策略[8-10]，仅需依赖视觉传感器；最后一种，也是本文的研究内容，是基于测距传感器的制导方法，即基于相对距离/相对距离变化率的制导策略，目前关于这方面的研究无论在国际还是国内均比较少。

基于测距传感器的制导方法最早用于地面智能车定距跟踪目标问题[11-12]，然而绝大多数此类制导律采用快速切换策略，未考虑最大航向角速率和最小转弯半径等的限制问题，因而无法应用于固定翼无人机制导系统。同时，在对制导律的稳定性进行证明和分析方面，众所周知，设计针对非线性系统的李雅普诺夫函数来完成稳定性证明是一项难度大且有挑战性的工作，目前绝大多数文献给出的是基于平衡点的线性系统稳定性证明。如文献[13-14]各自给出了一种基于距离/距离变化率的制导律，并给出了线性化以后的系统稳定性证明，但是这两种制导方法均有一个前提条件，即无人机与目标必须有一个较远的初始距离；对初始状态无限制并且给出李雅普诺夫直接法稳定性证明的例子在公开查阅到的文献中仅有文献[15-17]。这3篇文献给出了一种基于距离/距离变化率的制导律。然而，文献[15-17]中的制导律有如下共同的3点不足：首先，制导律的形式复杂。除制导增益外另有一个受限的设计参数需要确定，并且制导律中含有三角函数和反三角函数，这增加了制导律设计和机上解算的复杂性。其次，制导律的设计为在跟踪圆内仅将输入置为零的简单处理方法，这使得在某些条件下会出现无人机横穿整个轨迹圆的问题，这违背了定距跟踪的初衷。最后，文献[15-17]仅考虑了跟踪地面固定目标的问题，未考虑目标运动的情况。

本文提出了一种新型针对地面固定目标的基于距离/距离变化率的无人机盘旋跟踪制导律，克服了上述不足，对初始位置无限制，制导律的结构也更为简单，仅有一个设计参数，并且给出李雅普诺夫函数完成了稳定性证明。在此基础上，将该制导律推广到对地面移动目标的跟踪。

1 问题描述

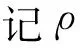
考察由式(1)描述的无人机二维动力学模型[3]：

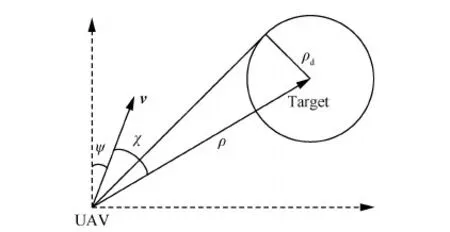
图1 无人机固定目标定距跟踪示意图Fig.1 Sketch diagram of tracking stationary target by UAV

(1)

式中：(x,y)为无人机位置；ψ为航向角；u为控制输入。若以(xt,yt)表示目标位置，则有

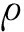
为了直接得到无人机与地面目标的相对关系，分析图1中的变量关系可知，式(1)还可以写成如式(2)所示的极坐标形式。

(2)

2 基于距离/距离变化率的制导律

(3)

此时，无人机动力学模型式(2)在制导律式(3)作用下的闭环系统可以表示为

(4)

下面对该闭环系统的稳定性进行分析与证明。

证明分两种情况进行证明：

此时有

此时有

考虑如下李雅普诺夫函数：

同样分两种情况进行证明：

此时有

此时有

证明考虑式(4)所示的闭环系统，定义

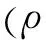
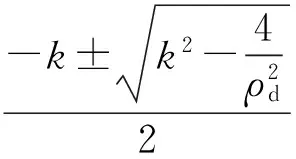
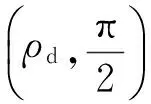
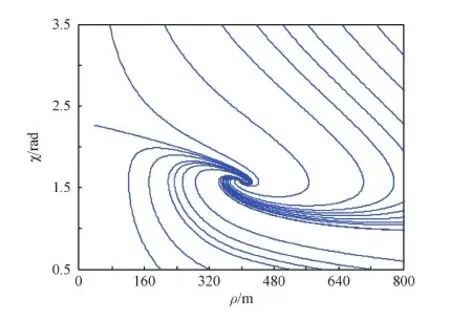
图2 闭环系统平衡点收敛过程 Fig.2 Convergence of equilibrium point of closed-loop system

3 移动目标制导律

当地面目标以速度vt(t)运动时，由式(2)推广可得无人机动力学模型为

(5)

v=vt+vm

(6)

式中：vt为地面目标速度矢量；vm为剩余速度矢量(下标m表示相对运动变量，下文同)，如图3所示。

由图3可见，上述分解可看作在一个以地面目标为原点的动坐标系中，无人机以vm为速度矢量围绕相对静止地面目标运动，则动力学模型式(5)可以改写为相对运动的形式，即

图3 无人机跟踪移动目标示意图Fig.3 Sketch diagram of tracking moving target by UAV

式中：vm为剩余速度矢量的大小。

显然式(7b)等价于

(8)

由式(7b)和式(8)得到启发，如果能得到um(t)和u(t)的关系，则原固定目标制导律可以依据此关系转换成移动目标制导律。

3.1 匀速运动地面目标

当地面目标匀速运动时，vt大小、方向均不变，而无人机速度v仅方向改变而大小不变，则对式(6)求导可得

(9)

式中：nm为vm的单位切向量；ω和ωm分别为与v和vm对应的角速度向量。由于式(9)左边两部分互相垂直，两边取模可得

|(ω×v)·nm|2+|ωm×vm|2=|ω×v|2

(10)

整理可得um(t)和u(t)有如下关系：

(11)

依据式(11)，对匀速移动目标新的制导律可以表示为

u=

(12)

进而可得无人机动力学模型的最终形式为

(13)

证明考虑如下李雅普诺夫函数：

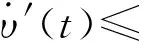
3.2 变速运动地面目标

则对变速移动目标新的制导律可以表示为

式中：

在上述制导律作用下的闭环系统与匀速运动时相同，因而仍然满足定理3。

同时，上述推导过程也表明，无论地面目标匀速或变速运动，在用定目标制导律进行推广时不可避免地需要引入额外的信号，即需要增加目标速度、航向以及无人机自身航向3个信号。当然这些信息除了可以从传感器获取外也可以采取依据现有信息进行推测的方法[19-20]。

4 仿真验证

为了验证前文提出的制导律和算法的有效性，在本节中分别针对地面固定目标、地面匀速运动目标和地面变速运动目标的跟踪问题进行仿真验证。在仿真开始时，无人机初始位置设置为(0，0) m，地面目标初始位置设置为(1 000，1 200) m；无人机其他仿真参数设置为：巡航速度为45 m/s，最大横滚角为30°，预定跟踪距离为400 m，飞行高度为3 000 m。

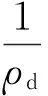
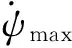
4.1 固定目标跟踪仿真

1) 远距固定目标

图4 远距固定目标轨迹Fig.4 Trajectory of tracking far stationary target

2) 近距固定目标

由图4～图7可见，无人机在跟踪地面固定目标时相对距离与视线角均有很好的收敛特性，并且无人机初始位置既可以在预设跟踪圆以外，也可以在跟踪圆以内。

图5 远距固定目标相对距离与视线角 Fig.5 Relative range and bearing angle of tracking far stationary target

图6 近距固定目标轨迹Fig.6 Trajectory of tracking close stationary target

3) 带传感器噪声仿真

图8(a)和图8(b)分别为文献[15]和本文制导律在大制导增益(k=5，文献[15]中的内圆半径ra=9.95)且传感器带有白噪声情况下的仿真结果(标准差σ=0.5)。由图8可见，文献[15]中的制导轨迹出现了反复以直线穿越跟踪圆的情况，这与定距跟踪的基本要求不符。经分析发现原因在于当增益较大时文献[15]中的内圆和外圆会过于接近，从而在传感器噪声作用下反复出现进入内圆的情况，而本文的制导律尽管收敛速度有所下降，但不会出现横穿跟踪圆的情况，因此制导策略更为合理。

图7 近距固定目标相对距离与视线角Fig.7 Relative range and bearing angle of tracking close stationary target

图8 不同方法下的制导轨迹Fig.8 Guidance trajectories according to different methods

当无人机的保持高度存在10 m误差时，对地面目标跟踪精度的影响小于0.2 m(400 m跟踪距离)，因此制导律对高度保持误差的敏感度不高。

4.2 移动目标跟踪仿真

1) 匀速运动目标

2) 变速运动目标

目标速度为

vt=15+2sin(t/10)

目标初始航向为45°，且

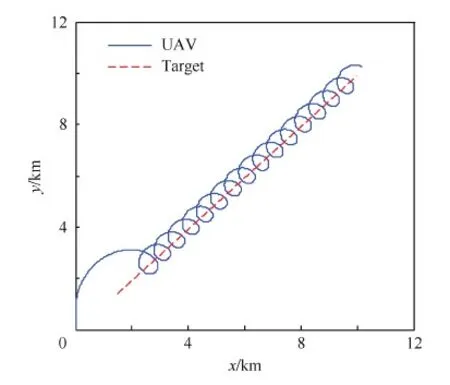
图9 跟踪匀速运动目标轨迹Fig.9 Trajectory of tracking target with constant speed

图10 跟踪匀速运动目标相对距离与视线角Fig.10 Relative range and bearing angle of tracking target with constant speed

图11 跟踪变速运动目标轨迹Fig.11 Trajectory of tracking target with time-varying speed

图12 跟踪变速运动目标相对距离与视线角Fig.12 Relative range and bearing angle of tracking target with time-varying speed

从图9～图12可见，无人机对匀速运动和变速运动目标距均可以实现稳定跟踪，相对距离的变化以预设跟踪距离为中心周期波动并限制在有限范围内，视线角围绕90°角仅有轻微波动。

5 结 论

1) 依据本文提出的制导律，无人机仅采用测距传感器就可以完成对固定目标的跟踪制导，不需要依赖传统的视线角信号，提高了无人机制导策略设计的灵活性。

2) 相比于现有同类制导律，其形式更为简洁，仅有一个设计参数且没有目前制导律中常见的三角函数或反三角函数，对无人机初始位置无限制，制导策略也更为合理，因而具有更广泛的应用范围。

3) 在制导律的设计过程中考虑了无人机最小转弯半径、最大滚转角等约束条件，适合固定翼无人机的实际工程应用。

4) 当地面目标做大范围无规律机动运动时，需要综合考虑无人机飞行约束条件和制导律参数的设计。

[1] 王道波, 王寅, 蒋琬玥， 等. 基于化学反应优化的多无人机地面移动目标协同观测航迹规划[J]. 中国科学: 技术科学, 2015, 45(6): 583-594.

WANG D B, WANG Y, JIANG W Y, et al. Unmanned aerial vehicles cooperative path planning for ground target tracking via chemical reaction optimization[J]. Scientia Sinica (Technologica), 2015, 45(6): 583-594 (in Chinese).

[2] HASHEMI A, CAO Y C, CASBEER D W, et al. Unmanned aerial vehicle circumnavigation using noisy range-based measurements without global positioning system information[J]. Journal of Dynamic Systems, Measurement and Control, 2015, 137(1): 1-10.

[3] 吴森堂, 费玉华. 飞行控制系统[M]. 北京: 北京航空航天大学出版社, 2005: 46-64.

WU S T, FEI Y H. Flight control system[M]. Beijing: Beihang University Press, 2005: 46-64 (in Chinese).

[4] 陈宗基, 魏金钟, 王英勋， 等. 无人机自主控制等级及其系统结构研究[J]. 航空学报, 2011, 32(6): 1075-1083.

CHEN Z J, WEI J Z, WANG Y X, et al. UAV autonomous control levels and system structure[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(6): 1075-1083 (in Chinese).

[5] TANG Z, OZGUNER U. Motion planning for multitarget surveillance with mobile sensor agents[J]. IEEE Transactions on Robotics, 2005, 21(5): 898-908.

[6] LIU C, MCAREE O, CHEN W H. Path-following control for small fixed-wing unmanned aerial vehicles under wind disturbances[J]. International Journal of Robust and Nonlinear Control, 2013, 23(1): 1682-1698.

[7] COCHRAN J, KRSTIC M. Nonholonomic source seeking with tuning of angular velocity[J]. IEEE Transactions on Automatic Control, 2009, 54(4): 717-731.

[8] DOBROKHODOV V, KAMINER I, JONES K, et al. Vision-based tracking and motion estimation for moving targets using small UAVs: AIAA-2006-6606[R]. Reston: AIAA, 2006.

[9] NIKI R, MATTEO Z. Camera pan-tilt gimbals robust control law for target tracking with fixed wing UAV[C]//Proceedings of AIAA Guidance, Navigation, and Control (GNC) Conference. Reston: AIAA, 2013: 19-22.

[10] DEGHAT M, SHAMES I, ANDERSON B D O, et al. Localization and circumnavigation of a slowly moving target using bearing measurements[J]. IEEE Transactions on Automatic Control, 2014, 59(8): 2182-2188.

[11] SHAMES I, DASGUPTA S, FIDAN B, et al. Circumnavigation using distance measurements under slow drift[J]. IEEE Transactions on Automatic Control, 2012, 57(4): 889-903.

[12] VARGA M, ZUFFEREY J C, HEITZ G, et al. Evolution of control strategies for fixed-wing drones following slow-moving ground agents[J]. Robotics and Autonomous Systems, 2015, 72(1): 285-294.

[13] MATVEEV A S, TEIMOORI H, SAVKIN A V. The problem of target following based on range-only measurements for car-like robots[C]// IEEE Conference on Desicision and Control and Chinese Control Conference. Piscataway, NJ: IEEE Press, 2009: 8537-8542.

[14] MATVEEV A S, TEIMOORI H, SAVKIN A V. Range-only measurements based target following for wheeled mobile robots[J]. Automatica, 2011, 47(1): 177-184.

[15] CAO Y C. UAV circumnavigating an unknown target under a GPS-denied environment with range-only measurements[J]. Automatica, 2015, 55(1): 150-158.

[16] CAO Y C. UAV circumnavigating an unknown target using range measurement and estimated range rate[C]//Proceedings of American Control Conference. Piscataway, NJ: IEEE Press, 2014: 4581-4586.

[17] CAO Y C, MUSE J, CASBEER D, et al. Circumnavigation of an unknown target using UAVs with range and range rate measurements[C]//Proceedings of the 52nd IEEE Conference on Decision and Control. Piscataway, NJ: IEEE Press, 2013: 3617-3622.

[18] KHALIL H K. Nonlinear systems[M]. 3rd ed. Upper Saddle River: Prentice Hall, 2002: 139-144.

[19] LI Z, HOVAKIMYAN N, DOBROKHODOV V, et al. Vision-based target tracking and motion estimation using a small UAV[C]//Proceedings of the 49th IEEE Conference on Decision and Control. Piscataway, NJ: IEEE Press, 2010: 2505-2510.

[20] OLIVEIRA T, ENCARNACAO P. Ground target tracking control system for unmanned aerial vehicles[J]. Journal of Intelligent & Robot Systems, 2013, 69(1): 373-387.

张民男， 博士， 副研究员。 主要研究方向： 无人机导航、 制导与控制。

Tel.: 025-84892308

E-mail: zhangmin@nuaa.edu.cn

田鹏飞男， 硕士研究生。 主要研究方向： 无人机制导系统设计。

E-mail: 1002717167@qq.com

陈欣男， 博士， 研究员。主要研究方向： 无人机飞行控制。

E-mail: chenxin@nuaa.edu.cn

*Correspondingauthor.Tel.：025-84892308E-mail:zhangmin@nuaa.edu.cn

UAVguidancelawforcircumnavigatingandtrackinggroundtargetanditsstabilityproof

ZHANGMin*,TIANPengfei,CHENXin

CollegeofAutomationEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing211106,China

Onetypicalapplicationofunmannedaerialvehicles(UAVs)ismadeforthemissionofcircumnavigatingandtrackinggroundtargets,andhowtocompletethetrackingtaskwithlimitedsensorinformationremainsahotspotofcurrentresearch.Thispaperdevelopsaguidancelawwhichreliesonlyondistancemeasuringsensor,anddoesnotneedtraditionalbearingsignalandlocationofUAVorgroundtarget.ALyapunovfunctionisderivedtoprovethestabilityoftheproposedguidancelaw.Thisguidancelawisextendedtothetrackingofmovinggroundtargetwithconstantandtime-varyingspeed.Comparingwithexistingones,thisguidancelawissuperiorwithsimplerstructure(onlyoneparameter)andmorereasonableguidancestrategy.Simulationresultsshowthattheproposedguidancelawcanaccomplishstabletrackingofstationaryandmovinggroundtargets.

unmannedaerialvehicle(UAV);circumnavigating;groundtarget;guidancelaw;stability

2015-10-30；Revised2015-12-25；Accepted2016-01-04；Publishedonline2016-01-080955

URL：www.cnki.net/kcms/detail/11.1929.V.20160108.0955.002.html

NationalNaturalScienceFoundationofChina(61174197)

2015-10-30；退修日期2015-12-25；录用日期2016-01-04； < class="emphasis_bold">网络出版时间

时间：2016-01-080955

www.cnki.net/kcms/detail/11.1929.V.20160108.0955.002.html

国家自然科学基金 (61174197)

*

.Tel.：025-84892308E-mailzhangmin@nuaa.edu.cn

张民， 田鹏飞， 陈欣. 一种无人机定距盘旋跟踪制导律及稳定性证明J． 航空学报,2016,37(11):3425-3434.ZHANGM,TIANPF,CHENX.UAVguidancelawforcircumnavigatingandtrackinggroundtargetanditsstabilityproofJ.ActaAeronauticaetAstronauticaSinica,2016,37(11):3425-3434.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0002

V279

A

1000-6893(2016)11-3425-10