基于自适应IMM的高超声速飞行器轨迹预测
2016-11-20翟岱亮雷虎民李炯刘滔
翟岱亮, 雷虎民, 李炯, 刘滔
空军工程大学 防空反导学院, 西安 710051
基于自适应IMM的高超声速飞行器轨迹预测
翟岱亮, 雷虎民*, 李炯, 刘滔
空军工程大学 防空反导学院, 西安 710051
为了给基于预测命中点法的高超声速飞行器中制导拦截提供先验知识,提出高超声速飞行器的轨迹预测方法。首先,给出高超声速环境下与目标姿态近似线性的气动参数;其次,针对气动参数作控制量的运动模型,设计自适应交互多模型(IMM)跟踪算法,并进行性能有效性验证;然后,根据气动参数特性和目标假设机动方式,设计基于最小二乘拟合的轨迹预测方法。通过对目标轨迹进行跟踪和预测仿真,预测100 s的位置误差均小于5 km,速度误差均小于100 m/s,结果表明基于自适应IMM的轨迹预测方法对有规律机动的目标进行轨迹预测,效果良好。
高超声速飞行器; 目标跟踪; 预测; 自适应; 交互多模型; 拟合
高超声速再入滑翔飞行器(Hypersonic Reentry-Glide Vehicle, HRGV)一般是指飞行马赫数大于5,能利用自身特殊的气动外形提供升力,在临近空间进行无动力滑翔飞行,执行全球快速打击任务的飞行器[1-2],典型代表有HTV-2和AHW。它具有机动能力强、弹道灵活多变、难于拦截等诸多优点,受到了高度重视。目前,各军事大国对HRGV的控制特性[3-4]、动力学特性[5-6]、轨迹优化[7-8]、热防护[9]以及跟踪[10-13]等问题进行了大量研究,而对于HRGV的拦截问题鲜有报道。
由于目标飞行速度很高,只能采用预测命中点法进行制导拦截,这就对目标的轨迹预测提出了要求。预测问题的实质就是要获知至少两个方面的信息:参量的当前状态分布和参量的变化规律,对于目标的轨迹预测而言,即为目标当前飞行状态和目标运动模型。通过目标跟踪可以获得目标的当前状态;而要获知目标未来时刻的运动模型,需要充分的关于目标的先验知识,包括目标的作战运用方式、机动方式、机动范围以及过去时刻的飞行规律等等。由于目标滑翔阶段飞行时间最长、受力影响因素最少,是防御的主要阶段,本文将以HTV-2的滑翔段为研究对象,进行目标跟踪和轨迹预测研究。
由于高超声速飞行器机动方式复杂多样,多模型方法是最具有潜力的跟踪方法[10-12]。多模型算法要求模型集中具有与目标机动模式匹配的运动模型,但是常用的机动模型与临近空间高超声速飞行器运动模型不匹配。文献[13]通过对目标进行气动分析,设计了基于气动参数的多模型跟踪算法,收到了较好的跟踪效果,但是,它所采用的气动参数与时间序列呈现高度非线性,不利于目标的轨迹预测。轨迹预测问题的实质是时间序列预测问题,简单地采用混沌时间序列预测[14]、神经网络[15]或灰色预测[16]等方法对历史状态数据进行处理,不仅预测精度不高,也不能满足对高超声速目标进行轨迹预测的实时性要求。期望的情况应该是通过预测某一能反映目标的运动特性且随时间的变化规律尽量简单(呈线性或周期性变化等)的参数,进而解算目标的轨迹。文献[17-19]通过对目标运动特性的分析,得到了某些反映目标运动特性的参数,但是这些参数随时间的变化不规律,不利于预测。因此,目标精确的高阶运动模型总是伴随着高度的非线性[20-21],无论对目标跟踪还是对轨迹预测均会增加数据处理难度,降低估计精度。为此,本文首先给出了一组与目标姿态近似线性的参数,然后基于此参数设计了带控制量的交互多模型(IMM)跟踪算法和轨迹预测算法,为高超声速飞行器的中长期轨迹预测提供了理论基础和方法指导。
1 运动模型
1.1 坐标系定义
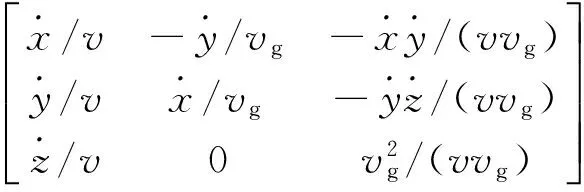
(1)

1.2 线性化参数
目标在VTCCS下的气动加速度aVTC是空气压强和气动参数α=[αdktdkcd]T的函数,这里表示为
(2)

通过采用斜激波理论、活塞理论、Prandtl-Meyer方程[3-6]以及黏性力工程计算方法[23]在临近空间高超声速环境下对HTV-2简化外形的受力情况进行建模[24],然后分析与目标气动特性相关的各参数,给出一组新气动参数αVTC=[αVαTαC]T,它与目标在VTCCS下气动加速度的关系可表示为
(3)
式中:P0为目标所处环境自由流压强。通过再入体运动方程[25]进行验证,证明了所给参数性能的有效性。
图1给出了目标在VTCCS下的初始高度、初始速度、攻角和滚转角均为定值时,式(2)中的气动参数以及式(3)中的气动参数随时间的变化曲线。

图1 半速度坐标系(VTCCS)下的目标气动参数Fig.1 Aerodynamic parameters of target in velocity-turn-climb coordinate system (VTCCS)
从图1中可以看出,目标以固定姿态飞行时,VTCCS下的气动参数变化非线性且不规律;而VTCCS下新气动参数近似线性,也就是说目标在飞行过程中新气动参数与目标在VTCCS下的相对姿态近似线性。
1.3 运动模型
为了表征目标飞行状态与目标气动参数的相互关系,采用以新气动参数αVTC为控制量的运动模型。
xk+1=Fxk+Gg+Gαuk+ωk
(4)

(5)
同理,可以得到以气动参数α为控制量时的运动模型。
分别将图1(b)中的新气动参数αVTC的真实值和其直线拟合值带入目标运动方程式(4),得到目标轨迹如图2所示。

图2 目标轨迹Fig.2 Target trajectory
从图2中可以看出,采用αVTC的线性拟合值生成的目标轨迹可以很好地逼近目标的真实轨迹,这就为后续目标跟踪,尤其是目标轨迹预测提供了有利条件。
2 自适应IMM跟踪
这里拟把气动参数作为机动控制输入建立模型集进行多模型跟踪,预期可获得较好的效果。IMM算法的关键步骤在于:① 模型集的设计[22,26],即设计能覆盖目标各种运动模式的模型集合;② 模型集自适应,即如何准确、及时地切换到正确的模型集。
2.1 模型集设计
2.1.1 模型集设计方法
把系统的模式建模为一个随机变量s:Ω→S,S为模式空间,Ω为样本空间。定义Fs(x)和fs(x)分别为s的累积分布函数(c.d.f.)和概率密度函数(p.d.f.)。把模型建模为一个离散随机变量r:Ω→M,M为随机变量r的取值范围,即M={r1,r2,…,rN},下标N表示模型的数量;模型的先验概率分布设为P{ri}。则模型集的设计就是寻找一个随机变量r去估计一个给定的随机变量s。常用的方法是最小概率分布误匹配设计[26],即已知Fs(x),给定某个误差ε,寻找一个随机变量r使其c.d.f.Fr(x)满足:
|Fs(x)-Fr(x)|≤ε
(6)
当s为矢量时,一般采用数论方法(Number-Theoretic Method, NTM)设计模型集。NTM的核心是在l维单位立方体Cl上找出一个Weyl意义上有限数量的低偏差离散点集。利用这些低偏差点集,可以生成代表某个连续分布函数F(x)的代表点。由于对于任意给定的c.d.f.F(x),总能找到一个低偏差离散点集,使它的经验分布函数Fn(x)逼近F(x),满足式(7)所示的距离度量:
(7)
因而,由这些代表点集可以构成具有最小概率分布误匹配的模型集合。当x的维数l小于10时,如果点集中需要的点数目较小,glp集合都是最好的。
定义glp集合:令[n,h1,h2,…,hl]为一个整矢量,满足1≤hi≤n,hi≠hj(i≠j),l (8) 式中:qui满足1≤qui≤n。则集合Pn={xu=[xu1,xu2,…,xul]}称为生成矢量[n,h1,h2,…,hl]的格子点集。如果Pn在所有可能的生成矢量中具有最小偏差,则Pn称为glp集。 2.1.2 运动模型集设计 在实际高超声速飞行过程中,影响目标机动的因素很多,对相关气动参数的建模需要大量飞行数据的支持[27]。由于缺乏相关的飞行数据,这里采用工程近似算法求解高超声速再入滑翔飞行器的气动分析问题,从而给出高超声速飞行器相关气动参数的范围。由于目标采用的是倾斜转弯机动,故在简化条件下,影响目标机动的内在参数仅由目标的攻角和滚转角决定。通过分析可知,攻角和滚转角对目标飞行距离的影响较大,为了不严重影响目标飞行距离,给定攻角范围为6°~12°,滚转角范围为0°~20°。通过仿真分析可得,目标的气动参数范围如表1所示。 注:考虑到目标气动分析的不精确性和模型集对目标机动模式的覆盖要求,这里对仿真所得的气动参数范围进行了适当扩大。 表1 气动参数范围Table 1 Scope of aerodynamic parameters 模型集设计的一个基本要求是覆盖目标的机动模式,另外,由于目标的机动情况对防御方来讲是未知的,这里假设各气动参数在其取值范围内均匀分布,进行模型集设计。通过滤波过程逐步收敛和模型集自适应策略,目标的机动模式估计值可以较快的收敛到目标的真实机动模式附近。首先采用最小模型集设计方法对各维度的气动参数构建均匀模型集,然后采用glp方法分别对气动参数α和αVTC设计三维10模型集和三维20模型集。 决定IMM算法性能优劣的关键在于其所使用的模型集合,设计或选取与目标真实运动匹配的最小模型集合成为该算法的一项关键技术。为了确保对整个模式空间以任意模式机动的飞行器的估计稳定性,采用以上设计的均匀模型集作为源模型集;同时,为了保证多模型跟踪的估计精度,把统计意义上距离真实模式最近的模式估计值增加到源模型集中,实现模型集自适应。则模型集可表示为 Mk=M′∪mc (9) 式中:Mk为k时刻的模型集;M′为源模型集;mc为k-1时刻的模式估计值。 图3 自适应交互多模型(IMM)算法示意图Fig.3 Sketch map of adaptive interactive multiple model (IMM) algorithm (10) 式中:μi和μmc分别为相应的模型权值。 为了验证本文设计的IMM算法的性能,采用预警雷达作为观测器,采用以气动参数αVTC和α作为控制量的两种运动模型,通过不敏卡尔曼滤波(Unscented Kalman Filter, UKF)算法进行跟踪。 测量方程为 zk=h(xk)+σ= (11) 式中:zk、h(xk)和σ分别为预警雷达的观测向量、量测方程和量测噪声;σr、σθ和σφ分别为预警雷达径向距离、俯仰角和方位角误差,均为均值为零的白噪声序列。这里给定目标初始状态为x1=[0 m 0 m 40 000 m 2 400 m/s 0 m/s 0 m/s]T,预警雷达部署位置为[7×105100]Tm,量测噪声标准差为[30 m 0.05° 0.05°]T。 从高超声速飞行器的研究现状可知,虽然高超声速助推滑翔飞行器具有横向机动能力,但是考虑到其控制稳定性和操纵性,未从公开文献中看到出于某种战术需求的典型横向机动方式。为验证本文提出气动参数的性能有效性和轨迹预测方法的有效性,这里假设目标始终以最大升阻比(即目标攻角为固定值)飞行,给定以下3种目标机动方式,分别为 方式1:目标始终保持20° 滚转角飞行。 方式2:目标滚转角以周期为80 s,幅度为20° 的正弦波机动飞行。 方式3:目标滚转角以周期为80 s,幅度为10° 的阶跃波机动飞行。 图4 3种机动方式下的跟踪误差Fig.4 Tracking errors of target under 3 different maneuver modes 比较图4中的跟踪结果可知,以气动参数αVTC作为控制量的模型的跟踪精度要优于以气动参数α作控制量的模型的跟踪精度;由于采用了模型集自适应机制,采用10模型集和20模型集进行跟踪时,精度相当;虽然采用20模型集时,收敛速度较快,但它所耗用的计算时间要远大于10模型集;还可以发现,机动方式1的跟踪误差(最终位置误差约150 m,速度误差约20 m/s)要高于机动方式2和机动方式3的跟踪误差(最终位置误差约50 m,速度误差约10 m/s),这主要是因为目标以机动方式1机动的轨迹末端与观测器的距离相对较远造成的,说明观测误差对目标跟踪精度的影响较大,这就对观测器的性能提出更高的要求;由于机动方式2和机动方式3类似,任一种跟踪方法对两种机动方式具有相同的跟踪效果。 目标轨迹预测问题同一般的状态估计问题一样,实质也是估计,即以历史数据为基础,经过特定算法给出所需要的信息。这里采用跟踪方法得到相关气动参数的估计结果,然后通过对过去时刻的气动参数进行处理,研究目标气动参数的变化规律,进而给出未来时刻的气动参数,则可以采用运动模型式(4)解算目标在未来时刻的状态信息,实现轨迹预测。 考虑到高超声速飞行器的任务规划和高超声速环境下流场变化等因素,目标实际轨迹变化情况复杂,需要充分利用关于目标运动的先验信息,而这在对抗环境中往往是不可得的。本文只对目标有规律飞行的轨迹预测问题进行了研究,以验证预测方法的可行性和有效性。 逼近实验数据的基本方法是曲线拟合,其中最常用的是最小二乘拟合[28-29],它适用的数学模型可以是线性函数和非线性函数。对于一组给定的数据(xk,yk),设计和确定一个函数模型y=f(x),使得函数f(x)在某种误差标准下与左右数据点(xk,yk)之间的距离最近,也就是说寻求一个最佳拟合函数。对于单个函数模型,使用最小二乘法只能获得一个拟合结果,计算相应的误差值,如果误差值没有达到要求,就要改用其他模型,直到满足要求为止。 函数模型的设计需要根据经验来选择,从图1 中可以看出,在攻角和滚转角为固定值时,新气动参数αVTC近似线性,同时考虑的到目标的周期性机动,采用一阶多项式和三角函数的复合函数f(a,tc)作为拟合函数模型给出气动参数变化曲线。 f(a,tc)=a(1)sin(a(2)tc+a(3))+ a(4)tc+a(5) (12) 式中:a为待拟合参数;tc为时间自变量。 通过第3节跟踪仿真分析,这里采用运动模型式(4)、模型数量为10的IMM算法通过UKF对上述机动方式1和机动方式3的目标轨迹进行跟踪,然后采用第3节介绍的预测方法进行轨迹预测,进行50次蒙特卡罗仿真。 3.2.1 预测精度分析 两种机动轨迹的跟踪和预测结果分别如图5和图6所示。3个分图分别表示目标气动参数αVTC的跟踪结果和预测100 s的结果、目标三维轨迹的跟踪结果和预测100 s的结果以及目标状态的跟踪误差和预测误差。图5(c)中的虚线分别为预测140 s、120 s和100 s时的误差;图6(c)中虚线分别为预测250 s、200 s、150 s和100 s时的误差。 从图5和图6的仿真结果中可以看出,本文提出的基于跟踪的预测方法对机动方式1和机动方式3的目标进行轨迹预测,均能收到比较理想的效果。 通过对气动参数αVTC的跟踪和预测可知,气动参数αV和αC在两种机动方式下均近似线性,跟踪效果较好;在机动方式2和机动方式3的情况下,由于目标滚转角周期变化,αT跟踪误差较大;通过上述给出的两个拟合函数模型,对3个气动参数历史数据进行拟合,均能收到较好的效果。 从目标三维轨迹的跟踪和预测结果中可以看出,在目标跟踪过程中,由于有观测数据的及时修正,跟踪估计结果能够很好地逼近目标真实轨迹;而预测轨迹存在误差积累,造成了与真实轨迹的偏差。 从目标状态的跟踪误差和预测误差中可以看出,不同机动方式、不同跟踪时长,预测100 s的位置误差均在5 km以下,速度误差均在100 m/s以下;预测时长越长,预测误差越大。另外,需要注意的是,由于初始初始模型误差较大,加上跟踪算法收敛速度较慢,当跟踪时间较短时,轨迹预测误差明显增大,这可从图5(c)和图6(c)中的第1条预测误差曲线看出。 图5 目标机动方式1的跟踪和预测结果 Fig.5 Tracking and prediction results of target under Maneuver 1 图6 目标机动方式3的跟踪和预测结果 Fig.6 Tracking and prediction results of target under Maneuver 3 3.2.2 实时性分析 运行环境为:Intel(R) Core(TM) i7 3.4 GHz处理器,8 G内存,Win7 64 Bit操作系统,运行平台为MATLAB 2012b。对两种机动轨迹进行跟踪和预测所需要的时间如表2所示。 已知程序运行步长为1 s,通过对比分析可知:单步跟踪时长远小于1 ms;跟踪时间越长,预测所需时间越长,这是因为随着跟踪时间的变长,气动参数估计精度越高,拟合所需的时间越短;采用三角函数式(12)对转弯参数αT进行拟合在预测过程中耗时最多,尤其是跟踪时间在100 s左右时,拟合所需时间远长于较长跟踪时间时拟合所需的时间;单步跟踪和预测时间小于1 s,满足实时轨迹预测要求。 表2 运算时间Table 2 Operation time 在实际应用中,一方面,高超声速飞行器的控制系统、作战运用原则以及自主机动规则等对拦截方来讲是未知的;另一方面,目标所处大气环境的变化存在一定程度的不确定性。这些都将使目标的机动形式更加复杂,仅能够从其外形与大气环境的相互作用中,获取其基本机动能力,对其进行某种最小意义上的限制,即不应对目标的飞行性能、参数做除了其最大飞行包络之外的过多假设。因此,如何对目标机动特性进行符合实际的限定,使它的运动表现出一定的规律性,又不失随机性,是下一步轨迹预测的重点和难点。因此,需要研究更多更有效的轨迹预测算法和拟合函数,这不仅对轨迹预测的精度提出了更高的要求;对轨迹预测的实时性也提出了严峻挑战,这从三角函数拟合所需的时间可见一斑。 本文在给出高超声速条件下与目标姿态近似线性的气动参数的基础上,通过设计自适应IMM跟踪算法和预测方法,对3种有规律机动的目标进行跟踪和轨迹预测,收到了较好的效果。 通过分析可知,本文设计的跟踪算法对任意机动的目标轨迹进行跟踪,效果良好;轨迹预测算法的精度和实时性对不同的目标机动方式较为敏感,这也是本文提出与目标姿态近似线性的气动参数的初衷。根据相关文献报道以及高超声速飞行器机动方式、控制性能等相关信息,目标只能进行长时小过载飞行。因此,可以推断目标的姿态在短时间内变化不大,这就为基于此气动参数的轨迹预测问题提供了有利条件。这不仅为研究复杂机动的高超声速飞行器轨迹预测问题提供了理论基础和方法指导,也为基于预测命中点法的高超声速飞行器的拦截制导提供了可能性。 [1] WALKER S H, SHERK J, SHELL D, et al. The DARPA/AF falcon program: The hypersonic technology vehicle#2 (HTV-2) flight demonstration phase: AIAA-2008-2539[R]. Reston: AIAA, 2008. [2] NORRIS J D, LAFFERTY J F, SMITH M S, et al. Design and aerodynamic calibration of the new AEDC hypervelocity wind tunnel No.9 mach 8 nozzle: AIAA-2005-4278[R]. Reston: AIAA, 2005. [3] ZHANG Y, XIAN B, DIAO C, et al. Robust tracking control design for a flexible air-breathing hypersonic vehicle[J]. Journal of Central South University, 2014, 21(1): 130-139. [4] LI H F, LIN P, XU D J. Control-oriented modeling for air-breathing hypersonic vehicle using parameterized configuration approach[J]. Chinese Journal of Aeronautics, 2011, 24(1): 81-89. [5] BOLENDER M A, DOMAN D B. Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle[J]. Journal of Spacecraft and Rocket, 2007, 44(2): 374-387. [6] ADAMOV N P, PUZYREV L N, KHARITONOV A M, et al. Damping characteristics of a reentry vehicle at hypersonic velocities[J]. Journal of Applied Mechanics and Technical Physics, 2014, 55(5): 870-876. [7] ZHAO J, ZHOU R. Reentry trajectory optimization for hypersonic vehicle satisfying complex constraints[J]. Chinese Journal of Aeronautics, 2013, 24(6): 1544-1553. [8] ZHAO J, ZHOU R, JIN X L. Progress in reentry trajectory planning for hypersonic vehicle[J]. Journal of Systems Engineering and Electronics, 2014, 25(4): 627-639. [9] 陆海波, 刘伟强. 迎风凹腔与逆向喷流组合热防护系统冷却效果研究[J]. 物理学报, 2012, 61(6): 064703-1-064703-6. LU H B, LIU W Q. Cooling efficiency investigation of forward-facing cavity and opposing jet combinatorial thermal protection system[J]. Acta Physica Sinica, 2012, 61(6): 064703-1-064703-6 (in Chinese). [10] 张翔宇, 王国宏, 李俊杰, 等. 临近空间高超声速滑跃式轨迹目标跟踪技术[J]. 航空学报, 2015, 36(6): 1983-1994. ZHANG X Y, WANG G H, LI J J, et al. Tracking of hypersonic sliding target in near-space[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6): 1983-1994 (in Chinese). [11] LIU Y, YAN X Q, LU G M. A high effective fuzzy synthetic evaluation multi-model estimation[J]. Sensors and Transducers, 2014, 163(1): 44-52. [12] ZHOU W D, ZHANG H B, LIAO C Y. Application of GMCPHD filter algorithm based on VSMM in multiple maneuvering targets tracking[J]. Systems Engineering and Electronics, 2013, 35(1): 9-14. [13] 李海宁, 雷虎民, 翟岱亮, 等. 面向跟踪的吸气式高超声速飞行器动力学建模[J]. 航空学报, 2014, 35(6): 1651-1664. LI H N, LEI H M, ZHAI D L, et al. Tracking oriented dynamics modeling of airbreathing hypersonic vehicles[J]. Acta Aeronautica et Asrtonautica Sinica, 2014, 35(6): 1651-1664 (in Chinese). [14] 孟庆芳, 张强, 牟文英. 混沌时间序列多步自适应预测方法[J]. 物理学报, 2006, 55(4): 1666-1671. MENG Q F, ZHANG Q, MU W Y. A novel multi-step adaptive prediction method for chaotic time series[J]. Acta Physica Sinica, 2006, 55(4): 1666-1671 (in Chinese). [15] 杨彬, 贺正洪. 一种GRNN神经网络的高超声速飞行器轨迹预测方法[J]. 计算机应用与软件, 2015, 32(7): 239-243. YANG B, HE Z H. Hypersonic vehicle track prediction based on GRNN[J]. Computer Applications and Software, 2015, 32(7): 239-243 (in Chinese). [16] 徐一帆, 谭跃进, 贺仁杰, 等. 海洋移动目标多模型运动预测方法[J]. 火力与指挥控制, 2012, 37(3): 20-25. XU Y F, TAN Y J, HE R J, et al. Multi-model prediction for maritime moving target motion[J]. Fire Control & Command Control, 2012, 37(3): 20-25 (in Chinese). [17] 秦雷, 李君龙, 周荻. 临近空间非弹道式目标HTV-2跟踪滤波与预报问题[J]. 航天控制, 2015, 33(2): 56-61. QIN L, LI J L, ZHOU D. The problems of tracking filter and prediction for non-ballistic target HTV-2 in the near space[J]. Aerospace Control, 2015, 33(2): 56-61 (in Chinese). [18] 王路, 邢清华, 毛艺帆. 助推-滑翔无动力跳跃飞行器轨迹预测[J]. 空军工程大学学报(自然科学版), 2015, 16(1): 24-27. WANG L, XING Q H, MAO Y F. A track forecasting algorithm of boost-glide unpropulsive skipping vehicle[J]. Journal of Air Force Engineering University (Natural Science Edition), 2015, 16(1): 24-27 (in Chinese). [19] 李广华, 张洪波, 汤国建. 高超声速滑翔飞行器典型弹道特性分析[J]. 宇航学报, 2015, 36(4): 397-403. LI G H, ZHANG H B, TANG G J. Typical trajectory characteristics of hypersonic glide vehicle[J]. Journal of Astronautics, 2015, 36(4): 397-403 (in Chinese). [20] LI X R, JILKOV V P. Survey of maneuvering target tracking. Part I: Dynamic models[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1333-1364. [21] LI X R, JILKOV V P. A survey of maneuvering target tracking. Part II: Ballistic target models[C]// Proceeding of SPIE Conference on signal and Data Processing of Small Targets. Bellingham: SPIE, 2001: 559-581. [22] LIANG Y Q, LI X R, HAN C Z, et al. A general systematic method for model-set design[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1505-1520. [23] 张栋, 唐硕, 李世珍. 吸气式高超声速飞行器粘性力工程计算方法[J]. 固体火箭技术, 2013, 36(3): 291-295. ZHANG D, TANG S, LI S Z. Engineering calculation method of viscous force for air-breathing hypersonic vehicle[J]. Journal of Solid Rocket Technology, 2013, 36(3): 291-295 (in Chinese). [24] 翟岱亮, 雷虎民, 李海宁, 等. 面向轨迹预测的高超声速飞行器气动性能分析[J/OL]. 固体火箭技术, (2015-11-15) [2015-11-19]. http://www.cnki.net/kcms/detail/61.1176.V.20160901.1626.002.html. ZHAI D L, LEI H M, LI H N, et al. Trajectory prediction oriented aerodynamic performances analysis of hypersonic vehicles[J/OL]. Journal of Solid Rocket Technology, (2015-11-15) [2015-11-19]. http://www.cnki.net/kcms/detail/61.1176.V.20160901.1626.002.html (in Chinese). [25] ISTRATIE V. Three-dimensional optimal skip entry with terminal maximum velocity[C]//Proceedings of AIAA Atmospheric Flight Mechanics Conference. Reston: AIAA, 1997: 19-26. [26] 孙福明. 机动目标跟踪状态估计与数据关联技术的研究[D]. 合肥: 中国科学技术大学, 2007: 41-62. SUN F M. Research on state estimation and data association of motion targets[D]. Hefei: University of Science and Technology of China, 2007: 41-62 (in Chinese). [27] 曾开春, 向锦武. 高超声速飞行器飞行动力学特性不确定分析[J]. 航空学报, 2013, 34(4): 798-808. ZENG K C, XIANG J W. Uncertainty analysis of flight dynamic characteristics for hypersonic vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(4): 798-808 (in Chinese). [28] CAO F, LI M. Spherical data fitting by multiscale moving least squares[J]. Applied Mathematical Modelling, 2015, 39(12): 3448-3458. [29] 陈跃宁, 徐征, 赵谡玲, 等. 最小二乘拟合计算有机薄膜晶体管迁移率的研究[J]. 物理学报, 2010, 59(11): 8113-8117. CHEN Y N, XU Z, ZHAO S L, et al. Research on least-squares fitting calculation of the field-effect mobility[J]. Acta Physica Sinica, 2010, 59(11): 8113-8117 (in Chinese). 翟岱亮男, 博士研究生。主要研究方向: 目标跟踪, 信息融合。 Tel.: 029-84789435 E-mail: quietzdl@126.com 雷虎民男, 博士, 教授, 博士生导师。主要研究方向: 飞行器导航、 制导与控制。 Tel.: 029-84789196 E-mail: hmleinet@21cn.com 李炯男, 博士, 副教授, 硕士生导师。主要研究方向: 飞行器导航、 制导与控制。 Tel.: 029-84789192 E-mail: graceful001@126.com 刘滔男, 博士研究生。主要研究方向: 飞行器导航、 制导与控制。 Tel.: 029-84789435 E-mail: ltloveder@sina.com *Correspondingauthor.Tel.:029-84789196E-mail:hmleinet@21cn.com TrajectorypredictionofhypersonicvehiclebasedonadaptiveIMM ZHAIDailiang,LEIHumin*,LIJiong,LIUTao SchoolofAirandMissileDefense,AirForceEngineeringUniversity,Xi’an710051,China Toaffordthepriorinformationforinterceptingthehypersonicvehiclethroughmidcourseguidancebasedonpredictedimpactpoint,astrategyfortrajectorypredictionofthehypersonicreentry-glidevehicleisproposed.Asetofaerodynamicparameters,whicharelinearlyrelatedtothetargetattitude,isgiven.Theadaptiveinteractivemultiplemodel(IMM)trackingalgorithmisdevelopedbasedonthedynamicmodelwithaerodynamicparametersbeingthecontrolinput.Theeffectivenessofthealgorithmisverified.Consideringthelinearcharacteristicoftheparametersandthesupposedmaneuveringmannersofthetarget,amethodfortrajectorypredictionbasedontheleast-squarefittingisdeveloped.Simulationsshowthatin100s,thepredictedpositionerrorsarelessthan5km,andthepredictedvelocityerrorsarelessthan100m/s,provingtheeffectivenessofthestrategyinpredictingthetrajectoriesofregularmaneuveringtargets. hypersonicvehicle;targettracking;prediction;adaptive;interactivemultiplemodel;fitting 2015-11-19;Revised2015-12-23;Accepted2016-02-17;Publishedonline2016-03-031635 URL:www.cnki.net/kcms/detail/11.1929.V.20160303.1635.002.html s:NationalNaturalScienceFoundationofChina(61573374,61503408);AeronauticalScienceFoundationofChina(20150196006,20140196004) 2015-11-19;退修日期2015-12-23;录用日期2016-02-17; < class="emphasis_bold">网络出版时间 时间:2016-03-031635 www.cnki.net/kcms/detail/11.1929.V.20160303.1635.002.html 国家自然科学基金 (61573374,61503408); 航空科学基金 (20150196006,20140196004) * .Tel.:029-84789196E-mailhmleinet@21cn.com 翟岱亮, 雷虎民, 李炯, 等. 基于自适应IMM的高超声速飞行器轨迹预测J. 航空学报,2016,37(11):3466-3475.ZHAIDL,LEIHM,LIJ,etal.TrajectorypredictionofhypersonicvehiclebasedonadaptiveIMMJ.ActaAeronauticaetAstronauticaSinica,2016,37(11):3466-3475. http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn 10.7527/S1000-6893.2016.0044 V249.1 A 1000-6893(2016)11-3466-10
2.2 模型集自适应方法



2.3 仿真分析


3 轨迹预测
3.1 轨迹预测方法
3.2 轨迹预测仿真分析



3.3 复杂机动目标轨迹预测方法分析
4 结 论
