机翼对螺旋桨发动机旋转颤振的影响研究

陈兆林， 杨智春， 谷迎松

西北工业大学 航空学院， 西安 710072

机翼对螺旋桨发动机旋转颤振的影响研究

陈兆林， 杨智春*， 谷迎松

西北工业大学 航空学院， 西安 710072

为了研究机翼对螺旋桨发动机旋转颤振的影响规律，揭示其影响机理，通过片条理论计算螺旋桨气动载荷，在MSC.NASTRAN软件平台上进行二次开发，对不同结构参数的吊舱-螺旋桨系统和机翼-吊舱-螺旋桨系统进行了旋转颤振分析。研究表明，机翼结构的弹性会大幅降低发动机俯仰模态频率，而小幅降低发动机偏航模态频率，从而改变两模态频率之差，影响模态耦合的程度，进而改变旋转颤振速度。另外，当发动机的运动与机翼翼面的运动耦合紧密时，机翼翼面的气动载荷能够显著提高发动机的旋转颤振速度。

旋转颤振； 影响机理； 模态耦合； 机翼； 螺旋桨

对于安装于飞机上的螺旋桨发动机，在一定飞行状态下，由于连接的柔性，其螺旋桨桨盘中心会沿椭圆轨迹做发散运动，这种动力学不稳定现象称之为旋转颤振，它是由螺旋桨运动与其诱导的非定常气动载荷耦合所致。

近年来，随着节能环保的设计理念在旅客机和通用飞机的设计中得到大力提倡，涡轮螺旋桨发动机飞机又重新受到青睐。而在结构设计方面，现代螺旋桨发动机飞机逐渐朝着采用轻质材料、加大机翼展弦比的方向发展，结构柔性的增加使得旋转颤振问题更加突出。另一方面，对于新型垂直起降飞机——倾转旋翼机，由于其发动机质量更大、桨叶更长、连接机构更复杂，使得螺旋桨-旋翼系统的动力学稳定性问题更加严重，这也促使人们对旋转颤振问题重新予以高度重视。

早在1938年，Taylor和Browne[1]首次提出了螺旋桨发动机发生旋转颤振的可能性，但直到1960年左右，两架涡桨发动机飞机由于旋转颤振而失事，旋转颤振问题才开始受到重视。随后，国内外的研究者开展了大量的研究工作。在理论研究方面，Reed等[2-4]采用片条理论计算螺旋桨气动载荷，建立了二自由度的吊舱-螺旋桨系统旋转颤振分析模型，通过变参数分析，详细阐述了该系统发生旋转颤振的机理，得出了旋转颤振稳定性与刚度、阻尼、枢轴点位置之间的关系。在试验研究方面，Bland等[5-6]通过风洞试验，分别研究了吊舱-螺旋桨系统和机翼-吊舱-螺旋桨系统的旋转颤振特性，并验证了文献[2-3]中螺旋桨气动载荷计算方法的准确性。Abbott等[7]以带有4个螺旋桨发动机的全机模型为研究对象，进行了风洞试验来研究其旋转颤振特性。文献[5-7]中所采用的风洞模型的螺旋桨均为无动力的，而Cecrdle和Malecek[8]设计制作了有动力螺旋桨的旋转颤振模型，并进行了试验研究。1989年，William和Ted[9]将Houbolt和Reed[3]的理论与NASTRAN软件相结合，发展了求解旋转颤振的新途径，并对吊舱-螺旋桨系统和机翼-吊舱-螺旋桨系统分别进行了旋转颤振分析，验证了该方法的可行性。Cecrdle[10]在此基础上结合NASTRAN软件的SOL200求解器研究了考虑旋转颤振后的螺旋桨发动机结构优化设计问题。

国内对旋转颤振问题的研究始于20世纪90年代。刘济科和赵令诚[11-12]考虑机翼的影响，建立了机翼-吊舱-螺旋桨系统的旋转颤振动力学方程，并提出了求解旋转颤振的双迭代算法。姚一龙和施辉[13]分析了旋转颤振稳定性边界与系统转动点位置、结构刚度的关系，研究了机翼对旋转颤振的影响。么振兴和姚一龙[14]简化了螺旋桨气动载荷的计算流程，分别分析了螺旋桨定转速和定前进比状态下的旋转颤振特性。郑秋风[15-16]通过试验对螺旋桨气动载荷的计算进行了修正，并分析了系统参数对旋转颤振的影响规律。在倾转旋翼机的旋转颤振研究方面，贾大伟和韩景龙[17]基于弹性机翼、刚体短舱和刚性桨叶的假设，分析了倾转旋翼机前飞时的旋转颤振特性。薛立鹏和张呈林[18]考虑桨叶的挥舞、摆振和变距运动，建立了前飞状态下全铰接式倾转旋翼-短舱-机翼系统旋转颤振分析模型。李治权和夏品奇[19]考虑发动机短舱与机翼之间连接的弹性，建立了倾转旋翼机前飞状态下11自由度旋转颤振模型。

早期的旋转颤振研究多从吊舱-螺旋桨系统入手，但发动机是安装在弹性机翼上的，因此研究机翼对发动机旋转颤振的影响是十分必要的，一些文献[3,6,11-13]对这一问题也有所涉及。多数的研究结论认为机翼可以提高发动机的旋转颤振速度，其解释通常简单地认为机翼起到阻尼器或吸振器的作用。但也有文献的分析结果表明，机翼也有可能会降低旋转颤振速度[11-12]或几乎对其没有影响[6,11-12]。

鉴于现有文献中，机翼对发动机旋转颤振影响规律的研究结论不相一致，影响机理的分析也不完善，本文研究了不同结构参数的吊舱-螺旋桨系统和机翼-吊舱-螺旋桨系统的旋转颤振特性。通过对计算结果的分析，总结出机翼对发动机旋转颤振的影响规律，揭示了其影响机理，并对相关文献中的理论分析结果和试验现象进行了合理的解释。

1 旋转颤振分析方法

1.1 二自由度吊舱-螺旋桨系统的旋转颤振分析

首先用简单的二自由度吊舱-螺旋桨系统来阐述旋转颤振分析方法。二自由度吊舱-螺旋桨系统如图1所示，该系统中采用刚性桨叶和刚性吊舱的假设，系统由俯仰方向和偏航方向的扭簧弹性连接于固定点上，两扭簧的弹性系数分别为Sθ和Sψ。系统仅有绕俯仰轴和偏航轴转动两个自由度，俯仰角位移为θ，偏航角位移为ψ。Ly、Lz、My、Mz分别为螺旋桨产生的作用在桨盘中心的气动力和气动力矩。dθ和dψ分别为桨盘平面到系统俯仰轴和偏航轴的距离；Ω为螺旋桨转速。

图1 二自由度吊舱-螺旋桨系统的旋转颤振分析模型Fig.1 Model for analyzing whirl flutter of two-degree of freedom nacelle-propeller system

系统的旋转颤振运动方程可以写为

(1)

式中：Ix为螺旋桨及发动机转子绕自转轴的转动惯量；Iy和Iz分别为系统绕俯仰轴和偏航轴的转动惯量；βθ和βψ分别为俯仰和偏航方向的黏性阻尼系数。

将式(1)写成矩阵的形式为

(2)

对式(2)进行特征值分析，得到两个虚部为正的特征值p1=γ1ω1+iω1、p2=γ2ω2+iω2，进而由γ1和γ2得到结构阻尼系数g1和g2，由ω1和ω2得到频率f1和f2。由一系列飞行速度V可以得到一系列g1、g2和f1、f2，画出V-g和V-f曲线，从而得到系统旋转颤振速度和颤振频率，即可完成二自由度系统旋转颤振问题的求解。

1.2 基于NASTRAN的旋转颤振分析

对于常规机翼的颤振分析，难以建立解析求解公式，却可以方便地利用NASTRAN软件建立结构有限元模型和气动力模型，然后通过该软件的SOL145求解器进行颤振分析，获得V-g、V-f曲线，求出颤振速度和颤振频率。但是，NASTRAN无法计算陀螺力矩和螺旋桨气动载荷，因此需要进行二次开发，才可以进行旋转颤振分析。

对于螺旋桨气动载荷的计算，采用片条气动力理论[3]，考虑空气压缩性和非定常气动力的滞后效应，借鉴文献[20]中的处理方式进行简化，并转化到图1的坐标系中，最终得到螺旋桨气动载荷的表达式为

(3)

(4)

其中：

(5)

(6)

式中：y和z分别为桨盘中心沿y和z方向的位移；ρ为空气密度；V为飞行速度，或来流速度；R为螺旋桨半径；S为桨盘面积，S=πR2；Np为桨叶的个数；a为桨叶二维翼型的不可压升力线斜率；c0为桨叶参考截面弦长；c为桨叶半径r处截面的弦长；μ为前进比J与圆周率之比，μ=J/π，J=πV/ΩR；η为桨叶截面的无量纲半径，η=r/R，r为桨叶任意截面半径；A为桨叶展弦比；Ma为来流马赫数。

将式(4)～式(6)代入式(3)中，得到螺旋桨气动载荷的矩阵表达形式为

(7)

式中：气动阻尼矩阵Ca和气动刚度矩阵Ka的表达式为

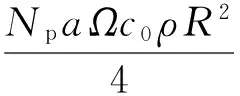
(8)

(9)

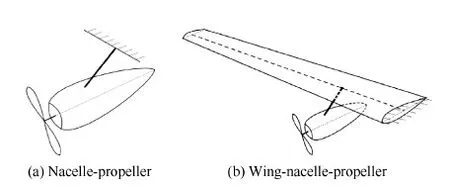
图2 旋转颤振分析模型示意图Fig.2 Sketch of models for analyzing whirl flutter

本文分别以图2所示的吊舱-螺旋桨系统和机翼-吊舱-螺旋桨系统为旋转颤振的分析对象来开展研究。吊舱-螺旋桨系统中，发动机通过挂架连接在固定界面上，而机翼-吊舱-螺旋桨系统中，发动机通过挂架连接在机翼主梁上，机翼的根部固支。

对于每一个分析模型，首先在NASTRAN软件中采用弹性梁单元和集中质量单元建立结构有限元模型，采用一个俯仰方向的扭簧和一个偏航方向的扭簧模拟发动机的挂架，对于机翼-吊舱-螺旋桨系统，还需要建立机翼翼面的气动力模型，从而获得常规颤振分析模型文件。然后计算出陀螺力矩和螺旋桨气动载荷，根据式(1)，将矩阵G-Ca和矩阵-Ka通过DMIG卡片的形式写入NASTRAN常规颤振分析模型文件中，得到旋转颤振分析模型文件。最后通过SOL145进行求解，即可求出旋转颤振速度和颤振频率，旋转颤振分析流程如图3所示。

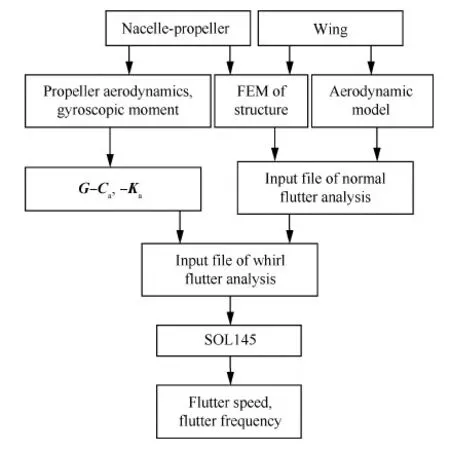
图3 基于NASTRAN的旋转颤振分析流程 Fig.3 Flow chart of whirl flutter analysis based on NASTRAN

2 机翼对发动机旋转颤振的影响

机翼作为发动机的支持结构，其弹性必然会对发动机的旋转颤振稳定性产生影响。另外，机翼上的气动载荷会对机翼的运动产生作用，进而影响发动机的运动。下面分别研究机翼结构弹性和机翼气动载荷对发动机旋转颤振的影响规律和影响机理。

在图2系统的有限元模型中，采用俯仰方向和偏航方向的扭簧模拟发动机挂架的刚度，两扭簧的弹性系数分别为Sθ和Sψ。记两扭簧的初始弹性系数为S0=9.5×105N·m，通过改变Sθ和Sψ调节挂架刚度，然后对图2(a)和图2(b)两系统分别做模态分析，得到不同挂架刚度下系统的固有频率。其中，吊舱-螺旋桨系统的发动机俯仰模态和偏航模态频率分别记为ωθ和ωψ，机翼-吊舱-螺旋桨系统的发动机俯仰模态和偏航模态频率分别记为ωθw和ωψw，计算结果如图4所示。

对比图4(a)和图4(b)，可以发现在任意发动机挂架刚度下，与不考虑机翼相比，考虑机翼后，机翼结构弹性会大幅降低发动机俯仰模态频率，而小幅降低发动机偏航模态频率。

图4 不同挂架刚度下旋转颤振模型的固有频率Fig.4 Natural frequency of whirl flutter models with different pylon stiffness

这是因为，发动机的俯仰运动与机翼的扭转运动相关，发动机的偏航运动受机翼的面内弯曲运动影响，而机翼的扭转刚度要远小于面内弯曲刚度。发动机安装在机翼上，相当于大幅降低了其俯仰方向的支持刚度，而其偏航方向的支持刚度降低较小，因此导致发动机俯仰模态频率大幅降低，而偏航模态频率小幅降低。

下面通过基于NASTRAN的旋转颤振分析方法，分别计算吊舱-螺旋桨系统和机翼-吊舱-螺旋桨系统在不同发动机挂架刚度下的旋转颤振速度。对于机翼-吊舱-螺旋桨系统，分为考虑和不考虑机翼上的气动载荷两种情况。结果如图5所示。

图5中各曲面左上角和右上角的平台表征的是由于俯仰或偏航刚度过小导致的发动机静发散速度，本文中对此不作研究。

结合图4和图5，可以观察到：

1) 减小发动机挂架的俯仰和偏航刚度会降低发动机俯仰模态和偏航模态固有频率，进而降低旋转颤振速度。

2) 图5中各曲面均向图中虚线处凹陷，而图5(a)中虚线基本对应图4(a)中发动机俯仰频率和偏航频率相等时的交线，图5(b)和图5(c)中虚线基本对应图4(b)中发动机俯仰频率和偏航频率相等时的交线。这表明，对于吊舱-螺旋桨系统和机翼-吊舱-螺旋桨系统，当发动机俯仰模态和偏航模态固有频率相近时，颤振速度显著降低。这是由于当两模态频率相近时，陀螺效应造成的模态耦合最为严重。

基于以上结果，可以总结出机翼对旋转颤振的影响规律和影响机理，下面通过取图5中的曲线abc进行说明，如图6(a)所示。在曲线abc上，Sθ/S0+Sψ/S0=2。曲线abc上各点对应的模型的固有频率可由图4得到，如图6(b)所示。

图5 不同挂架刚度下旋转颤振模型的旋转颤振速度Fig.5 Whirl flutter speed of whirl flutter models with different pylon stiffness

记吊舱-螺旋桨系统的发动机俯仰、偏航模态的固有频率ωθ和ωψ之差的绝对值为Δω，机翼-吊舱-螺旋桨系统的发动机俯仰、偏航模态的固有频率ωθw和ωψw之差的绝对值为Δωw。

图6 不同挂架刚度下吊舱-螺旋桨系统和机翼-吊舱-螺旋桨系统的旋转颤振速度和固有频率Fig.6 Whirl flutter speed and natural frequency of nacelle-propeller system and wing-nacelle-propeller system with different pylon stiffness

2.1 机翼结构弹性的影响

对比图6中吊舱-螺旋桨系统和机翼-吊舱-螺旋桨系统不考虑机翼气动载荷的情况，分析图中的a、b和c三点，可以发现：

1)a点：ωθ>ωψ。考虑机翼弹性后，ωθw相比ωθ大幅下降，而ωψw相比ωψ小幅下降，导致Δωw<Δω，即发动机的俯仰和偏航模态频率之间的差距减小，使得两模态间的耦合加剧。另一方面，固有频率降低也会对旋转颤振稳定性产生不利影响，两种因素共同作用，从而导致旋转颤振速度降低。

2)b点：ωθ≈ωψ，Δω≈0。考虑机翼弹性后，ωθw相比ωθ大幅下降，而ωψw相比ωψ小幅下降，导致Δωw>Δω，即发动机的俯仰和偏航模态固有频率之间的差距增大，减弱了两模态的耦合程度，从而提高旋转颤振稳定性，但是由于固有频率降低带来的不利影响的存在，使得颤振速度增幅很小。

3)c点：ωθ<ωψ。考虑机翼弹性后，ωθw相比ωθ大幅下降，而ωψw相比ωψ小幅下降，导致Δωw>Δω，即发动机俯仰和偏航模态频率之间的差距增大，减弱了两模态间耦合程度，且此时这种因素占主导地位，因此使得旋转颤振速度明显提高。

从上述分析中可以总结出，机翼结构弹性会大幅降低发动机俯仰模态频率，而小幅降低发动机偏航模态频率，从而会对旋转颤振产生两方面的影响：① 发动机俯仰、偏航模态频率降低，会对旋转颤振稳定性产生不利影响；② 发动机俯仰、偏航模态频率降低的幅度不同，会改变两模态频率之间的差距，影响模态耦合的程度，进而改变旋转颤振速度。

根据结构参数的不同，若不考虑机翼时，发动机偏航模态频率高于或接近俯仰模态频率，机翼结构弹性会使两模态频率之差增大，则会对旋转颤振稳定性产生有利影响；若不考虑机翼时，发动机偏航模态频率低于俯仰模态频率，且考虑机翼后机翼为发动机提供的支持刚度足够大，那么机翼结构弹性会使两模态频率之差减小，则会对旋转颤振稳定性产生不利影响。

机翼结构弹性通过两方面的影响共同作用，最终导致旋转颤振速度增大或减小，一般来说，当发动机俯仰、偏航模态频率之差足够大时，第2个方面的影响占主导地位。

2.2 机翼气动载荷的影响

对比图6中的机翼-吊舱-螺旋桨系统考虑与不考虑机翼气动载荷两种情况。

可以发现，在任意发动机挂架刚度下，与不考虑机翼气动载荷相比，考虑机翼气动载荷总会提高旋转颤振速度。

下面进一步分析这种影响的变化规律。保持Sθ/S0=Sψ/S0，改变挂架刚度，对机翼-吊舱-螺旋桨系统进行旋转颤振分析，分为考虑和不考虑机翼气动载荷两种情况，结果如图7所示。

图7 不同挂架刚度下机翼-吊舱-螺旋桨系统旋转颤振速度(Sθ/S0=Sψ/S0)Fig.7 Whirl flutter speed of wing-nacelle-propeller system with different pylon stiffness (Sθ/S0=Sψ/S0)

由图7可以看到，机翼气动载荷对旋转颤振的增稳作用随挂架刚度的增大而逐渐增大。当挂架刚度较小时，机翼气动载荷对旋转颤振几乎无影响。这是因为，只有当挂架刚度足够大时，发动机的运动与机翼翼面的运动耦合紧密，机翼翼面的气动阻尼才会发挥显著作用，抑制翼面的运动，进而抑制发动机的运动，从而提高旋转颤振速度。

3 发动机安装位置的影响

记机翼的展长为L，发动机安装位置到翼根的距离为l。在前文的分析中，发动机均是安装在l=0.276L位置处。下面改变发动机的安装位置，进行模态分析和旋转颤振分析，研究发动机安装位置对旋转颤振的影响，结果如图8所示。图8(a)、图8(b)和图8(c)中模型的挂架刚度分别对应图6中的a、b和c三点。

图8说明，发动机安装位置对旋转颤振具有两方面的影响。

1) 随着发动机安装位置远离翼根，机翼对发动机提供的支持刚度逐渐降低，使得发动机俯仰和偏航模态频率逐渐降低，但始终保持俯仰模态频率降低的幅度大于偏航模态，从而产生下述现象：图8(a)中随着l/L的增大，ωθw和ωψw逐渐减小，而Δωw先减小后增大，使得仅考虑机翼结构弹性的旋转颤振速度呈现先减小后增大的趋势。图8(b)中随着l/L的增大，ωθw和ωψw逐渐减小，Δωw逐渐增大，在l/L<0.25时，两种因素的作用相互抵消，使得机翼结构弹性对旋转颤振的影响微小。l/L>0.25后，Δωw增大的影响占主导地位，使得机翼结构弹性对旋转颤振的增稳作用逐渐增大。图8(c)中随着l/L的增大，ωθw和ωψw逐渐减小，Δωw逐渐增大，且Δωw增大的影响始终占主导地位，使得机翼结构弹性对旋转颤振的增稳作用逐渐增大。

图8 发动机安装位置对旋转颤振的影响Fig.8 Effect of engine’s location on whirl flutter

2) 发动机安装位置靠近翼根时，发动机运动与机翼翼面的运动几乎不耦合，从而使得机翼气动载荷对旋转颤振影响微小。随着发动机安装位置远离翼根，发动机运动与机翼翼面的运动耦合逐渐加剧，使得机翼气动载荷对旋转颤振的增稳作用逐渐增大。

4 对文献中结果的解释

综合考虑机翼结构弹性和机翼气动载荷的影响，总结出机翼对发动机旋转颤振的影响规律如下：

1) 若不考虑机翼时，发动机偏航模态固有频率高于或接近俯仰模态固有频率，则考虑机翼会提高旋转颤振速度，提高的幅度与挂架刚度、发动机安装位置等系统参数相关。

2) 若不考虑机翼时，发动机偏航模态频率低于俯仰模态频率，且考虑机翼后机翼为发动机提供的支持刚度足够大，则考虑机翼会降低旋转颤振速度。

根据上述规律，可以合理解释相关文献中对该问题的理论分析结果和试验现象。

Bennett和Bland[6]通过大量试验研究了机翼对发动机旋转颤振的影响，其采用的试验模型A、B和C的发动机偏航、俯仰模态频率很接近，类似图6中的b点，模型D的偏航频率高于俯仰频率，类似图6中的c点，因此对于模型B、C和D，其试验结果均表明机翼可以提高旋转颤振速度。对于模型A，一方面ωθ≈ωψ，机翼结构弹性造成的发动机俯仰、偏航模态频率降低和两模态频率之差变大的影响相互抵消，使得机翼结构弹性对旋转颤振的影响很小；另一方面ωθ和ωψ均太小，使得发动机运动和机翼翼面运动耦合很弱，机翼气动载荷对旋转颤振影响微小。因此，试验结果中机翼对模型A的旋转颤振无明显影响。

在姚一龙和施辉[13]采用的分析模型中，ωψ≈1.85ωθ，类似于图6中的c点，因此其计算结果表明机翼可以提高旋转颤振速度。

而在刘济科和赵令诚[12]所研究的模型中，ωθ=1.6ωψ，类似图6中的a点，因此其分析结果显示机翼可以降低旋转颤振速度。

采用本文研究结果对文献中结果进行的合理解释，证明了本文关于机翼对发动机的旋转颤振影响规律和影响机理研究结果的正确性和普适性。

5 结 论

1) 机翼结构的弹性会大幅降低发动机俯仰模态频率，而小幅降低发动机偏航模态频率。一方面，降低发动机俯仰、偏航模态频率会对旋转颤振稳定性产生不利影响；另一方面，发动机俯仰、偏航模态频率降低的幅度不同，会改变俯仰、偏航模态频率之差，影响到模态耦合的程度，进而影响旋转颤振特性。机翼结构弹性对旋转颤振的影响是这两方面因素的叠加。

2) 当发动机的运动与机翼翼面的运动耦合紧密时，机翼翼面的气动载荷能够显著提高发动机的旋转颤振速度。

3) 机翼通过机翼结构弹性和机翼气动载荷这两方面因素，共同对发动机旋转颤振特性产生影响。

4) 发动机安装位置能够改变机翼为发动机提供的支持刚度，以及发动机运动与机翼翼面运动的耦合程度，从而改变机翼结构弹性和机翼气动载荷对旋转颤振特性的影响程度。

[1] TAYLOR E S, BROWNE K A. Vibration isolation of aircraft power plants[J]. Journal of the Aeronautical Sciences, 1938, 6(2): 43-49.

[2] REED W H III, BLAND S R. An analytical treatment of aircraft propeller precession instability: NASA TN D-659[R]. Washington, D.C.: NASA, 1961.

[3] HOUBOLT J C, REED W H III. Propeller-nacelle whirl flutter[J]. Journal of the Aerospace Sciences, 1962, 29(3): 333-346.

[4] REED W H III. Review of propeller-rotor whirl flutter: NASA TR R-264[R]. Washington, D.C.: NASA, 1967.

[5] BLAND S R, BENNETT R M. Wind-tunnel measurement of propeller whir flutter speeds and static stability derivatives and comparison with theory: NASA TN D-1807[R]. Washington, D.C.: NASA, 1963.

[6] BENNETT R M, BLAND S R. Experimental and analytical investigation of propeller whirl flutter of a power plant on a flexible wing: NASA TN D-2399[R]. Washington, D.C.: NASA, 1964.

[7] ABBOTT F T, NEALE KELLY J H, HAMPTON K D. Investigation of propeller-power-plant autoprecession boundaries for a dynamic-aeroelastic model of a four-engine turboprop transport airplane: NASA TN D-1806[R]. Washington, D.C.: NASA, 1963.

[8] CECRDLE J, MALECEK J. Design and development of new whirl flutter aeroelastic demonstrator[C]//55th AIAA/ASME/ASCE/AHS/ASC Structure, Structural Dynamics, and Materials Conference. Reston: AIAA, 2014.

[9] WILLIAM P R, TED L R. Propeller/nacelle whirl flutter addition to MSC/NASTRAN[C]//Proceedings of the 1989 MSC World User’s Conference. Los Angeles: MacNeal Schwendler Corp., 1989.

[10] CECRDLE J. Analysis of twin turboprop aircraft whirl-flutter stability boundaries[J]. Journal of Aircraft, 2012, 49(6): 1718-1725.

[11] 刘济科, 赵令诚. 考虑弹性机翼影响的旋转颤振的动力学方程[J]. 机械强度, 1993, 15(4): 10-13.

LIU J K, ZHAO L C. Dynamic equations for whirl flutter considering wing elasticity[J]. Journal of Mechanical Strength, 1993, 15(4): 10-13 (in Chinese).

[12] 刘济科, 赵令诚. 考虑弹性机翼影响的旋转颤振方程的求解方法[J]. 机械强度, 1994, 16(2): 32-35.

LIU J K, ZHAO L C. A solving process for equations of whirl flutter considering wing elasticity[J]. Journal of Mechanical Strength, 1994, 16(2): 32-35 (in Chinese).

[13] 姚一龙, 施辉. 涡桨发动机飞机的螺旋颤振分析[J]. 民用飞机设计与研究, 1996(4): 3-9.

YAO Y L, SHI H. Whirl flutter analysis of a turboprop aircraft[J]. Civil Aircraft Design and Research, 1996(4): 3-9 (in Chinese).

[14] 么振兴, 姚一龙. 某型飞机螺旋颤振特性分析[C]//第八届全国空气弹性学术交流会. 北京: 中国空气动力学会空气弹性专业委员会, 2003: 117-122.

YAO Z X, YAO Y L. Whirl flutter analysis for a type of aircraft[C]//Proceedings of 8th National Forum on Aeroelasticity. Beijing: Committee of Aeroelasticity, Chinese Society of Aerodynamics, 2003: 117-122 (in Chinese).

[15] 郑秋风. 涡桨发动机飞机的螺旋颤振分析及实验[D]. 北京: 北京航空航天大学, 2012: 8-58.

ZHENG Q F. Analysis and experiment studies on whirl flutter of turboprop aircraft[D]. Beijing: Beihang University, 2012: 8-58 (in Chinese).

[16] 郑秋风. 机翼—涡桨发动机系统的旋转颤振参数影响实验[C]//第十三届全国空气弹性学术交流会. 北京: 中国空气动力学会空气弹性专业委员会, 2013: 155-159.

ZHENG Q F. Experiments of parameter effect on whirl flutter of wing-turboprop engine system[C]//Proceedings of 13th National Forum on Aeroelasticity. Beijing: Committee of Aeroelasticity, Chinese Society of Aerodynamics, 2013: 155-159 (in Chinese).

[17] 贾大伟, 韩景龙. 倾转旋翼机回转颤振研究[J]. 直升机技术, 2007(3): 45-51.

JIA D W, HAN J L. Study on whirl flutter of tiltrotor[J]. Helicopter Technique, 2007(3): 45-51 (in Chinese).

[18] 薛立鹏, 张呈林. 前飞状态倾转旋翼机气弹稳定性建模[J]. 航空动力学报, 2009, 24(2): 255-261.

XUE L P, ZHANG C L. Modeling study on tilt-rotor’s aeroelastic stability in cruise flight[J]. Journal of Aerospace Power, 2009, 24(2): 255-261 (in Chinese).

[19] 李治权, 夏品奇. 倾转旋翼机回转颤振及桨毂中心运动图像[J]. 中国科学: 科学技术, 2014, 44(3): 286-294.

LI Z Q, XIA P Q. Whirl flutter and rotor hub center’s motion image of tiltrotor aircraft[J]. Scientia Sinica (Technologica), 2014, 44(3): 286-294 (in Chinese).

[20] 陈兆林, 杨智春, 谷迎松, 等. 吊舱-螺旋桨系统旋转颤振分析[C]//第十四届全国空气弹性学术交流会. 北京: 中国空气动力学会空气弹性专业委员会, 2015.

CHEN Z L, YANG Z C, GU Y S, et al. Analysis of whirl flutter of pylon-propeller system[C]//Proceedings of 14th National Forum on Aeroelasticity. Beijing: Committee of Aeroelasticity, Chinese Society of Aerodynamics, 2015 (in Chinese).

陈兆林男， 博士研究生。主要研究方向： 旋转颤振、 壁板颤振和能量有限元。

E-mail: eagle985@163.com

杨智春男， 博士， 教授， 博士生导师。主要研究方向： 气动弹性力学、 结构动力学和结构健康监测。

Tel.: 029-88460461

E-mail: yangzc@nwpu.edu.cn

谷迎松男， 博士， 副教授， 硕士生导师。主要研究方向： 非线性气动弹性力学和气动伺服弹性力学。

E-mail: guyingsong@nwpu.edu.cn

*Correspondingauthor.Tel.：029-88460461E-mail:yangzc@nwpu.edu.cn

Effectofwingonwhirlflutterofpropellerengine

CHENZhaolin,YANGZhichun*,GUYingsong

SchoolofAeronautics，NorthwesternPolytechnicalUniversity,Xi’an710072,China

Inordertoinvestigatetheeffectsofwingonwhirlflutterofpropellerengineandrevealtheunderlyingmechanism,thewhirlflutterspeedofthenacelle-propellersystemandthewing-nacelle-propellersystemunderdifferentstructureparametersisanalyzed.Thestriptheoryisappliedtocalculatetheaerodynamicloadingofthepropeller,andamethoddevelopedfromMSC.Nastranisusedtoaccomplishwhirlflutteranalysis.Theresultsindicatethat,theelasticityofwingstructurecansignificantlydecreasethenaturalfrequencyofengine’spitchmode,andslightlydecreasethenaturalfrequencyofengine’syawmode.Thiscouldchangethedifferencebetweenthenaturalfrequenciesofbothmodes.Thedegreeofcouplingbetweenengine’spitchmodeandyawmodewouldthenbeinfluencedtocausethechangeinwhirlflutterspeed.Inthecaseoftightcouplingbetweenthemotionoftheengineandthewingsurface,theaerodynamicloadingofthewingsurfacecansignificantlyincreasethewhirlflutterspeedoftheengine.

whirlflutter;effectmechanism;modecoupling;wing;propeller

2015-12-11；Revised2015-12-30；Accepted2016-01-05；Publishedonline2016-01-221408

URL：www.cnki.net/kcms/detail/11.1929.V.20160122.1408.004.html

s：NationalNaturalScienceFoundationofChina(11472216);The“111”ProjectofChina(B07050)

2015-12-11；退修日期2015-12-30；录用日期2016-01-05； < class="emphasis_bold">网络出版时间

时间：2016-01-221408

www.cnki.net/kcms/detail/11.1929.V.20160122.1408.004.html

国家自然科学基金 (11472216)； 高等学校学科创新引智计划 (B07050)

*

.Tel.：029-88460461E-mailyangzc@nwpu.edu.cn

陈兆林， 杨智春， 谷迎松． 机翼对螺旋桨发动机旋转颤振的影响研究J． 航空学报,2016,37(11):3351-3360.CHENZL,YANGZC,GUYS.EffectofwingonwhirlflutterofpropellerengineJ.ActaAeronauticaetAstronauticaSinica,2016,37(11):3351-3360.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0008

V215.3+4

A

1000-6893(2016)11-3351-10