一种适用于三维混合网格的GMRES加速收敛新方法

张健， 邓有奇， 李彬， 张耀冰

中国空气动力研究与发展中心 计算空气动力研究所， 绵阳 621000

一种适用于三维混合网格的GMRES加速收敛新方法

张健*， 邓有奇， 李彬， 张耀冰

中国空气动力研究与发展中心 计算空气动力研究所， 绵阳 621000

为提高流场计算收敛效率，发展了一套适用于三维混合网格Naiver-Stokes方程求解的并行广义最小残差(GMRES)隐式时间推进方法。该方法由科学计算可移植扩展工具包(PETSc)中的Krylov子空间求解器实现，线性方程系统中的系数矩阵直接以显式给出以提高算法的稳定性。为进一步提高GMRES方法的收敛速度，对非结构网格的序号进行了重排序，使得系数矩阵的非零元素尽量向主对角线靠近。利用所发展的GMRES方法，完成了对ONERA-M6机翼、AIAA阻力预测会议通用研究模型(CRM)等算例的计算，计算结果与试验结果吻合良好。通过与其他隐式推进方法进行比较，对算法的收敛特性进行了研究。结果表明，所发展的GMRES方法计算更加稳定，残差下降速度相对LU-SGS(Lower-Upper Symmetric Gauss-Seidel)方法更快，尤其是气动力系数向着收敛解逼近的速度更加明显，提高了计算效率。

混合网格； 收敛效率； 隐式时间推进方法； GMRES； PETSc； 网格重排序

计算流体力学(Computational Fluid Dynamics, CFD)技术在近些年来取得了飞速发展，这使得求解复杂的三维流动问题更加易于实现。但随着工业界所研究问题的不断深入，所关注部件细节的更加详尽，一些工程外形也变得越来越复杂，从而导致相应网格的生成工作变得更加困难，时间开销也更大。尽管非结构混合网格技术在处理复杂外形方面相对于结构网格有一定优势，但通常为了取得更为精确的计算结果，其所需的网格量依然十分巨大。由此生成出一个大型的非线性耦合方程系统求解问题，需要大量的迭代时间才能得到一个收敛的流场。因此，对于解决大型工程问题找到一个快速有效的时间推进方法十分必要。

常用的时间推进技术包括显式的Runge-Kutta法[1]，隐式的LU-SGS(Lower-Upper Symmetric Gauss-Seidel)方法[2]等，其应用已较为成熟。隐式策略相对显式策略能够选取更大的时间步长，在很大程度上提高收敛速度。现今，多重网格技术[3]作为一种流行的加速收敛技术，通过在不同疏密程度的网格之间迭代循环计算，来消除不同频次的误差，以达到加速收敛的目的。但在一些复杂情况下，通过全局融合法融合细网格生成的粗网格可能具有不规则性，致使疏密网格之间没有好的插值、延拓算子，导致多重网格技术存在鲁棒性问题。另一种更加复杂的隐式策略就是Krylov子空间方法，Krylov子空间方法最初用来求解大规模矩阵问题，在有些情况下能够达到超线性甚至二次收敛的效果。Krylov子空间类型的方法有很多种，在CFD应用中最广泛的是广义最小残差(Generalized Minimal Residual, GMRES)方法[4], GMRES方法通过Arnoldi过程构造Krylov子空间的正交基和求解一个最小二乘法问题，在Krylov子空间上选择最优解，使每一步子迭代时的残差模最小。由于这个过程本身是面向全频率的残差，所以GMRES方法不需要结合多重网格加速技术，避免了多重网格不鲁棒的问题。GMRES方法在结构网格以及二维非结构CFD代码中已经有过成功的应用[5-6]，Xia等[7]将其应用在间断有限元算法(Discontinuous Galerkin, DG)上，燕振国等[8]将其应用在高阶耗散紧致格式上也都取得了不错的效果。本文的目的旨在将GMRES方法应用于复杂三维混合网格流场求解计算上，探索出适用于大型三维工程问题的加速收敛技术，以达到减少收敛时间，提高计算效率的目的。

PETSc(Portable, Extensible Toolkit for Scientific Computation)科学计算可移植扩展工具包是美国能源部ODE2000支持开发的20多个ACTS(Advanced Computational Testing and Simulation)工具箱之一，主要用于在分布式存储环境高效求解偏微分方程组及相关问题[9]。对于大规模线性方程组，PETSc提供了丰富的Krylov子空间迭代方法和各种预条件子。PETSc具有高性能、可移植等优点，并在CFD 领域的并行应用获得了相当的成功，其中较为典型的PETSc-FUN3D[10]获得了1999年的戈登·贝尔特别奖[11]，国内屈崑等[12]将其应用在CFD数学模型的线性化方法上。本文将在自主研发的三维混合网格流场求解器MFlow[13]的基础上，结合PETSc数学工具包实现GMRES时间推进算法。通过显式计算线性系统的系数矩阵，来提高GMRES算法的稳定性。同时，针对非结构网格编号顺序随机的问题，对网格序号进行重排序，得到带宽减小的系数矩阵，以提升GMRES的计算效率。并通过对M6机翼及AIAA阻力预测会议(DPW)标模等算例的计算验证，同时结合原有LU-SGS方法计算结果的对比分析，完成了对适用于混合网格流场求解加速收敛技术的研究。

1 控制方程及数值方法

三维可压缩流Navier-Stokes方程表达式为

(1)

式中：U为守恒变量；FI为无黏通量；FV为黏性通量；Ω为控制单元体积；S为单元面面积。

1.1 隐式时间离散

对方程式(1)进行空间离散后，得到如下半离散形式：

(2)

式中：M为质量矩阵(Mass Matrix)，对于基于格心的求解策略，M用单位矩阵；RI为残差，下标I代表对应的控制单元。

将式(2)改写成差分形式得到隐式离散格式：

(3)

式中：Δt为时间步长；上标n为当前时间迭代步；β为0～1之间的系数，一般取1较为鲁棒，取0则退化为显式格式。

对于隐式求解策略，需要估算出新的时间步上的残差：

(4)

式中：∂R/∂U一般称为通量雅克比矩阵(Flux Jacobian)。将式(4)代入式(3)，整理简化得到线性方程组的形式：

(5)

式中：

(6)

1.2 GMRES方法

本文的主要工作就是针对式(5)形式的线性系统进行求解，不同的求解方法构成了不同的隐式时间推进方法。

(7)

对于大型问题，为减小内存开销，一般采用重启型GMRES方法。通过在有限的Krylov子空间下反复重启迭代GMRES方法，直到残差收敛到预定值，算法的具体过程如下所示：

Forl=1,mDom次重启迭代

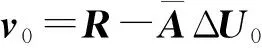
r0=P-1v0预处理

v1=r0/β

Forj=1,kDo 内迭代

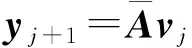
wj+1=P-1yj+1预处理

Fori=1,jDo Gram-Schmidt

hi,j=wj+1·vj

wj+1=wj+1-hi,jvj

End Do

hj+1,j=wj+1Hessenberg矩阵

vj=wj+1/hj+1,jKrylov向量

End Do

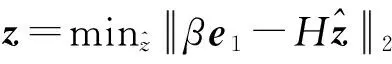
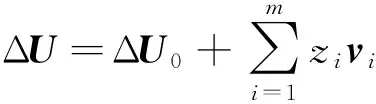
ΔU0=ΔU重启

End Do

1.3 隐式系统矩阵

在一般的GMRES方法实现过程中，雅克比矩阵都是以某一向量内积的形式出现，所以矩阵向量乘都以差分近似的无矩阵方法实现，即

(8)

然而，这个方法却存在两个问题。首先，小量ε的大小取值依赖于不同的问题，如果流动变化剧烈很有可能导致求解的不稳定。其次，在每一个迭代中需要额外计算一个残差向量，增加了计算量[14]。因此，本文尝试利用显式设置雅可比矩阵来解决上述问题。

通量雅克比矩阵可以分解为对流通量雅可比矩阵和黏性通量雅可比矩阵，即

(9)

式中：NF为单元面个数；ΔSIJ为相邻单元I、J之间单元面面积。黏性通量雅克比计算较为复杂，一般利用其谱半径简化得到

(10)

式中：ρIJ为密度；γIJ为比热比；μL和μT分别为层流黏性系数和湍流黏性系数；PrL和PrT分别为层流和湍流Prandtl数。对于无黏通量，根据Roe通量差分裂格式：

(11)

(12)

(13)

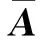
1.4 网格重排序

步骤1从某一个单元开始(尽量是物面边界单元)，定义其网格单元所属超平面序号Np为1。

步骤2寻找超平面Np所包括网格的相邻网格, 若相邻网格还无所属超平面, 则将其超平面序号定义为Np+1。

步骤3重复步骤2直到所有网格都有其对应的超平面为止。

步骤4从序号为1的超平面起按序号从小到大依次对每个超平面上的网格进行编号, 即得到了排序后的网格编号。

图1给出了一个简单的二维非结构网格示例图，右侧给出了其对应的系数矩阵。很明显，网格编号的无序性导致矩阵非零元素的分布无特定规律。图2给出了经过上述重排序算法之后的结果，可以看到，矩阵的非零元素更加向对角线靠近，矩阵的带宽明显减小。

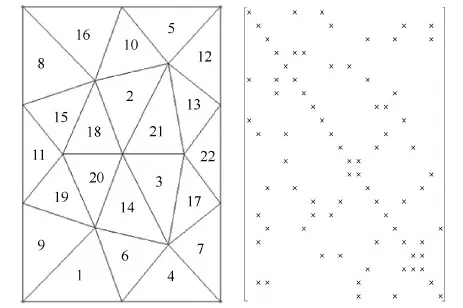
图1 二维非结构网格(左)及相应隐式算子矩阵(右)Fig.1 2D unstructured grid(left) and associatedimplict operator matrix(right)

图2 重排序后的网格及带宽减小后的矩阵Fig.2 Reordered grids and reduced bandwidth matrix

1.5 结合PETSc库并行实现GMRES方法

PETSc中提供了多个库，类似于C++中的类，每个库都有相应的接口来进行数据的设置或者方程的求解，其框架图[9]如图3所示。

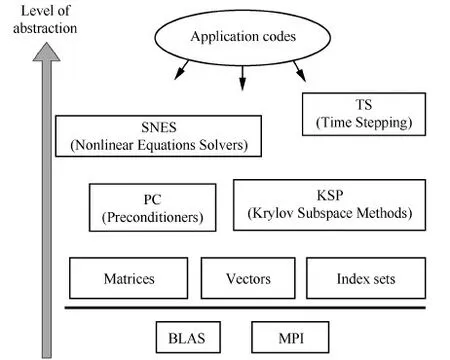
图3 PETSc库框架图[9]Fig.3 Organization of PETSc libraries[9]

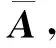
图4 网格并行划分示意图Fig.4 Example of grid’s parallelization

图5 装配好的并行块稀疏矩阵示意图Fig.5 Assembled sparse parallel matrix in block

2 数值模拟结果与分析

本节通过对ONERA-M6机翼和AIAA阻力预测会议标模等算例进行计算，对比了改进后的GMRES和其他隐式策略，并研究了多重网格、网格重排序和CFL数等因素对算法收敛速度的影响。所有算例的计算都是通过自主开发的基于混合网格的大型CFD计算软件MFlow完成。MFlow软件基于MPI并行化，使用标准C++语言编写，采用Roe迎风格式[17]计算通过控制体单元面的无黏通量，通过中心格式计算黏性项，湍流模型选取Spalart-Allmaras一方程模型[18]。

2.1 ONERA-M6机翼绕流流场模拟

ONERA-M6机翼是一个根弦约为0.8 m，半展长约为1.2 m的后掠机翼，剖面形状为对称翼型。ONERA-M6机翼绕流问题经常用作考核外流流场解算程序的标准算例。

首先选取来流马赫数为0.839 5，迎角为3.06° 的计算状态对程序进行验证。计算网格如图6所示，网格总量大约为80万，分24核并行计算完成。

图6 ONERA-M6机翼计算网格Fig.6 Computational grids of ONERA-M6 wing

GMRES方法的重启次数采用KSP求解器默认的30次，预处理选取支持并行的Jacobi预处理器。图7是本文发展的方法计算得到的机翼上表面等压力系数Cp分布图，由图中可以很清晰地看到计算结果捕捉到了“λ”型激波结构。图8是机翼沿展向90%的剖面压力系数分布，可以看到GMRES和LU-SGS两种隐式方法计算的结果一致，前缘吸力峰值和激波位置的捕捉十分准确，与试验数据[19]吻合较好，充分验证了新方法的正确性。

为测试不同方法对收敛特性的影响，针对此算例，分别利用LU-SGS和GMRES两种隐式算法进行计算。理论上，GMRES方法的CFL数可以取的很大，但由于残差呈高度非线性，初始几步迭代可能导致初场远远偏离稳定解[20]。因此本文先在一系列粗网格上利用LU-SGS计算一定步数，再将结果插值到细网格上得到初始场。这个过程耗时较少，对于整个收敛过程可以忽略不计，并保证各个不同算法从相同的初场进行启动，便于对比分析。在之后的计算中，分别应用单重网格(SG)LU-SGS，多重网格V循环LU-SGS，GMRES(Origin)和网格重排序(Reorder)后的GMRES进行计算。

图7 ONERA-M6机翼压力系数分布云图Fig.7 Pressure coefficient contours of ONERA-M6

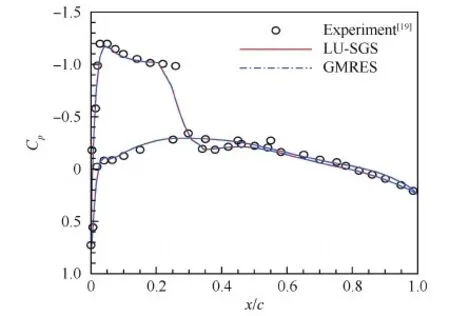
图8 ONERA-M6机翼90%展向剖面压力系数分布Fig.8 Pressure coefficient distributions at 90% span of ONERA-M6 wing

图9给出了不同算法随迭代步数以及迭代时间变化的收敛特性曲线。由图可以明显看到，残差下降5个量级，GMRES和多重网格V循环LU-SGS所用步数差不多，GMRES稍微少一点。由于各个算法每一个时间步耗时不同，考查收敛效率重点需要看收敛所需时间。可以看到，用GMRES和多重网格的LU-SGS耗时相当，比单重LU-SGS残差下降5个量级大概要快1倍左右。而GMRES方法在经过了网格重排序后有明显加速收敛效果，特别是收敛过程的前期残差的下降要更快一些。

在工程实践中，判断计算收敛与否主要看气动力是否收敛到稳定值。图10是升力系数随计算时间的变化曲线，重排序后的GMRES方法计算升力系数向稳定值逼近速度最快，原始的GMRES方法次之，随后是多重网格LU-SGS，最慢的是单重的LU-SGS。

图9 不同推进方法残差收敛特性比较 Fig.9 Comparison of residual convergence property between different methods

图10 不同方法升力系数收敛过程比较 Fig.10 Comparison of lift coefficient convergence property between different methods

2.2 CRM标模计算

AIAA阻力预测会议的计算外形是NASA的通用研究模型(Common Research Model，CRM)[21]。该模型由机身和机翼组成，其中机身是典型的商业运输机机身，机翼是跨声速超临界机翼。该外形在NASA Langley National Transonic Facility和NASA Ames 11-ft风洞都进行了详尽的试验[22]。本文所使用的MFlow软件的计算结果也曾参与了第五次阻力预测会议(DPW5)[23]的数据对比[24]。

DPW提供了多套标准网格，本文选取了DPW4[25]提供的一套三棱柱/四面体非结构网格，以及DPW5的一套中等大小的纯六面体网格进行计算，DPW5的外形相比DPW4少了水平尾翼，其表面网格及对称面网格分别如图11和图12 所示。

为了考察隐式算法的收敛特性，对上述两个算例进行了计算，计算状态均选取来流马赫数为0.85、迎角为2°和雷诺数为5.0×106，其中DPW4三棱柱/四面体网格总数大约为2 128万，分120个核并行计算完成，DPW5六面体网格总数大约为511万，分48个核并行计算完成，两套网格y+均为1。

图11 DPW4三棱柱/四面体网格Fig.11 Prism/tetra grid of DPW4

图12 DPW5六面体网格Fig.12 Hex grid of DPW5

首先对DPW4外形进行计算，之前已经考察了网格重排序和多重网格技术的加速收敛效果，所以这里直接采用重排序后的GMRES和多重网格的LU-SGS方法进行对比，同时还对比了利用式(12)简化后对角占优的系统矩阵(以下简称GMRES_D方法)的效果。为考察CFL数大小对算法收敛性的影响，分别选取CFL=50，100，200进行了计算。图13是计算残差随计算时间下降图，可以看到GMRES方法整体收敛要比LU-SGS方法快，而且通过增大CFL数能够明显加速收敛。对于GMRES_D方法，残差下降到10-3后下降速度减缓，可能是因为系统矩阵简化导致。对于本文所发展的GMRES方法，CFL数最多只能取到100，但残差下降速度依然是最快的。

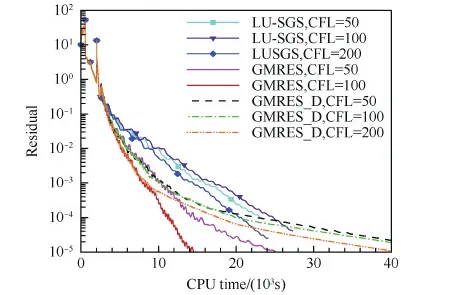
图13 不同方法及CFL数残差下降曲线(DPW4) Fig.13 Residual histories of different methods and different CFL numbers (DPW4)

图14给出的是升力系数收敛曲线对比，通过局部放大图可以明显看到采用GMRES方法，尤其是CFL=100时，升力系数很快收敛为稳定值，而LU-SGS方法计算的升力系数依然在剧烈振荡。

对DPW5外形计算过程中，同样采用不同方法和不同CFL数进行了计算。但是利用多重网格对LU-SGS进行加速时，计算不稳定残差发散，所以不得不改用单重网格进行计算。图15给出了不同算法的残差收敛曲线。从图中看到GMRES方法的残差下降速度明显比LU-SGS方法快。对于GMRES方法，CFL数从50提高到100收敛加速明显。而对于LU-SGS方法，将CFL数提高到100对残差下降没有明显影响。相同CFL数下，GMRES方法比GMRES_D方法收敛更快，CFL取100时残差振荡较为明显，但整体呈快速下降趋势。

图14 升力系数收敛曲线Fig.14 Histories of lift coefficient convergence

图15 不同算法及CFL数残差下降曲线(DPW5) Fig.15 Residual histories of different methods and different CFL numbers (DPW5)

图16给出了不同算法计算的阻力系数的收敛曲线图，对于GMRES方法，尤其是CFL=100时，在经过初期的振荡之后很快稳定到收敛解，而相同CFL数条件下用LU-SGS方法计算至少需要数倍以上的CPU时间。

图16 阻力系数收敛曲线Fig.16 Histories of drag coefficient convergence

3 结 论

1) GMRES方法是一个高效稳定的时间推进方法，能够适应不同复杂外形、不同类型网格的计算。

2) 相比于多重网格加速后的LU-SGS方法，GMRES方法能够取得相当甚至更快的残差下降速度，特别是在相同CFL数下气动力收敛加速效果更加明显。GMRES方法能够适应大的CFL数计算，提高CFL数能够明显提高收敛效率。

3) 对非结构网格编号进行重排序有利于提高GMRES方法的收敛效率。

4) 利用对流通量雅克比矩阵谱半径对通量雅克比矩阵简化，保证系统矩阵主对角占优能够增加算法的鲁棒性，但可能对于加速收敛效果产生不利影响。

本文所发展的GMRES加速收敛新方法，通过显式计算出通量雅克比矩阵实现，加速收敛效果明显，旨在为解决复杂三维流场计算中，尤其对于混合网格解算器，多一种时间推进算法选择，以提高工程效率。虽然GMRES方法在复杂三维流动问题求解上展现出高效、鲁棒的特点，但是隐式算法的收敛效率受到多方面因素影响，例如网格质量、流动特性等。此外，本文程序针对个别算例的稳定性受限于CFL数，在下一步工作中将针对此作进一步研究。

[1] JAMESON A, SCHMIDT W, TURKEK E. Numerical solutions of the euler equations by finite volume methods using Runge-Kutta time-stepping schemes： AIAA-1981-1259[R]. Reston: AIAA, 1981.

[2] YOON S, JAMESON A. Lower-upper symmetric gauss-seidel method for the euler and naiver-stokes equations[J]. AIAA Journal, 1988, 26(9): 1025-1026.

[3] JAMESON A. Multigrid algorithms for compressible flow calculations, multigrid method II[M]. Berlin: Springer Verlag, 2006： 166-201.

[4] SAAD Y, SCHULZ M H. GMRES: A generalized minimum residual algorithm for solving nonsymmetric linear systems[J]. SIAM Journal on Scientific and Statistcal Computing, 1986, 7: 856-869.

[5] WIGTON L B, YOUNG D P, YU N J. GMRES acceleration of computational fluid dynamics codes: AIAA-1985-1494[R]. Reston: AIAA, 1985.

[6] KNOLL D A, MCHUGH P R. Inexact Newton’s method solutions to the incompressible Navier-Stokes and energy equations using standard and matrix-free implementations: AIAA-1993-3332[R]. Reston: AIAA, 1993.

[7] XIA Y D, LUO H, NOURGALIEV R. An implicit hermite WENO resconstruction-based discontinuous Galerkin method on tetrahedral grids[J]. Computers & Fluids, 2014, 96(5): 406-421.

[8] 燕振国, 刘化勇, 毛枚良, 等. 基于高阶耗散紧致格式的GMRES方法收敛特性研究[J]. 航空学报, 2014, 35(5): 1181-1192.

YAN Z G, LIU H Y, MAO M L, et al. Convergence property investigation of GMRES method based on high-order dissipative compact scheme[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(5): 1181-1192 (in Chinese).

[9] BALAY S, ABHYANKAR S, ADAMS M, et al. PETSc users manual[EB/OL]. (2014-06-30)[2015-07-01]. http://www.mcs.anl.gov/petsc/documentation/index.html.

[10] ANDERSON W K, GROPP W D, KAUSHIK D K, et al. Achieving high sustained performance in an unstructured mesh CFD application[C]//Proceedings of the 1999 ACM/IEEE Conference of Supercomputing. New York: IEEE, 1999.

[11] 钟英, 张理论, 刘巍. PETSc及典型开源流体力学应用[J]. 计算机应用, 2013, 33(S2): 63-66.

ZHONG Y, ZHANG L L, LIU W. PETSc and its typical open-source computational fluid dynamics application[J]. Journal of Computer Applications, 2013, 33(S2): 63-66 (in Chinese).

[12] 屈崑, 李记超, 蔡晋生. CFD数学模型的线性化方法及其应用[J]. 航空学报, 2015, 36(10): 3218-3227.

QU K, LI J C, CAI J S. Method of linearizing computational fluid dynamics model and its applications[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(10): 3218-3227 (in Chinese).

[13] 张耀冰, 邓有奇, 吴晓军, 等. DLR-F6翼身组合体数值计算[J]. 空气动力学学报, 2011, 29(2): 163-169.

ZHANG Y B, DENG Y Q, WU X J, et al. Drag prediction of DLR-F6 using MFlow unstructured mesh solver[J]. Acta Aerodynamica Sinica, 2011, 29(2):163-169 (in Chinese).

[14] XIA Y D, LUO H, FRISBEY M, et al. A set of parallel, implicit methods for a reconstructed discontinuous Galerkin method for compressible flows on 3D hybrid grids[J]. Computers & Fluids, 2014, 98: 134-151.

[15] BLAZEK J. Computational fluid dynamics principles and applications[M]. Oxford: Elsevier Science Ltd., 2001: 419-420.

[16] 李劲杰, 王刚, 史爱明, 等. 基于非结构网格流场计算的网格重排序[J]. 航空计算技术, 2005, 35(3): 25-28.

LI J J, WANG G, SHI A M,et al. Reordering of 3D unstructured grids for computing efficiency improvement[J]. Aeronautical Computer Technique, 2005, 35(3): 25-28 (in Chinese).

[17] LUO H, BAUM J D, LOHNER R. An improved finite volume scheme for compressible flows on unstructured grids: AIAA-1995-0348[R]. Reston: AIAA, 1995.

[18] SPALART P R, ALLMARAS S R. A one equation turbulence model for aerodynamic flows: AIAA-1992-0439[R]. Reston: AIAA, 1992.

[19] SCHMITT V, CHARPIN F. Pressure distributions on the ONERA-M6 wing at transonic mach numbers, experimental data base for computer program assessment: AGARD AR-138-B1[R]. [S.l.]: AGARD, 1979.

[20] 康忠良, 阎超. 适用于混合网格的并行GMRES+LUSGS方法[J]. 空气动力学学报, 2013, 31(2): 225-230.

KANG Z L, YAN C. Parallel GMRES+LU-SGS method for mixed grids[J]. Acta Aerodynamica Sinica, 2013, 31(2): 225-230 (in Chinese).

[21] VASSBERG J C, DEHAAN M A, RIVERS S M, et al. Development of a common research model for applied CFD validation studies: AIAA-2008-6919[R]. Reston: AIAA, 2008.

[22] MELISSA B R, ASHLEY D. Experimental Investigation of the NASA common research model in the NASA langley national transonic facility and NASA Ames 11-ft transonic wind tunnel: AIAA-2011-1126[R]. Reston: AIAA, 2011.

[23] LEVY D W, LAFLIN K R, TINOCO E N, et al. Summary of data from fifth AIAA CFD drag prediction workshop: AIAA-2013-0046[R]. Reston: AIAA, 2013.

[24] GONG X, CHEN J, ZHOU N, et al. The effects of turbulence model corrections on drag prediction of NASA common research model: AIAA-2014-3171[R]. Reston: AIAA, 2014.

[25] VASSBERG J, TINOCO E, MANI M, et al. Summary of date from fourth AIAA CFD drag prediction workshop: AIAA-2010-4547[R]. Reston: AIAA, 2010.

张健男， 硕士， 研究实习员。主要研究方向： 计算空气动力学。

Tel: 0816-2463271

E-mail: j-zhang@foxmail.com

邓有奇男， 博士， 研究员， 博士生导师。主要研究方向： 计算空气动力学。

Tel: 0816-2463005

E-mail: cai@cardc.cn

李彬男， 博士， 助理研究员。主要研究方向： 计算空气动力学。

Tel: 0816-2463276

E-mail: leebin2008@hotmail.com

张耀冰男， 博士， 副研究员。主要研究方向： 计算空气动力学。

Tel: 0816-2463276

E-mail: zhyb_super@sina.cn

URL：www.cnki.net/KCMS/detail/11.1929.V.20160302.1449.008.html

*Correspondingauthor.Tel.：0816-2463271E-mail:j-zhang@foxmail.com

AnewmethodtoaccelerateGMRES’sconvergenceapplyingtothree-dimensionalhybridgrid

ZHANGJian*,DENGYouqi,LIBin,ZHANGYaobing

ComputationalAerodynamicInstituteofChinaAerodynamicResearch&DevelopmentCenter,Mianyang621000,China

Toimprovetheconvergenceefficiencyofsolvingtheflowfield,aparallelimplicittimeintegrationmethodgeneralizedminimalresidual(GMRES)isappliedtoathree-dimentionalhybridgridNavier-Stokessolver.ThemethodisimplementedbasedonaKrylovsubspacesolverinthescientificcomputationtoolkitportable,extensibletoolkitforscientificcomputation(PETSc).Thecoefficientmatrixoflinearsystemisprovidedexplicitlytostabilizethescheme.Inordertoacceleratetheconvergencemorespecifically,thecellindexesofunstructuredgridarereorderedsuchthatthesystemmatrix’snonzeroelementsareclusteredclosetothemaindiagonal.ThemethodisappliedtosimulationsofONERA-M6wingandAIAADragPredictionWorkshopmodelCRM.Theresultsshowgreatagreementwithexperimentaldata.Comparisonsaremadebetweendifferentimplicitschemes.TheGMRESmethoddevelopedinthispapershowsmorerobustnessandtheresidual’sconvergencehasasignificantspeedupcomparedwithLU-SGSmethod.Moreover,themethodhasafasterspeedapproximatingtothesteadystateofaerodynamiccoefficient.Itgreatlyimprovesthecomputationalefficiency.

hybridgrid;convergenceefficiency;implicittimeintegrationmethod;GMRES;PETSc;gridreorder

2015-11-25；Revised2015-12-27；Accepted2016-01-24；Publishedonline2016-03-021449

2015-11-25；退修日期2015-12-27；录用日期2016-01-24； < class="emphasis_bold">网络出版时间

时间：2016-03-021449

www.cnki.net/KCMS/detail/11.1929.V.20160302.1449.008.html

*

.Tel.：0816-2463271E-mailj-zhang@foxmail.com

张健， 邓有奇， 李彬， 等． 一种适用于三维混合网格的GMRES加速收敛新方法J． 航空学报,2016,37(11):3226-3235.ZHANGJ,DENGYQ,LIB,etal.AnewmethodtoaccelerateGMRES’sconvergenceapplyingtothree-dimensionalhybridgridJ.ActaAeronauticaetAstronauticaSinica,2016,37(11):3226-3235.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0038

V211.3; O355

A

1000-6893(2016)11-3226-10